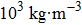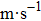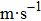† Corresponding author. E-mail:
We develop a model for calculating the radiation force on spherically symmetric multilayered particles based on the acoustic scattering approach. An expression is derived for the radiation force on a multilayered sphere centered on the axis of a Gaussian standing wave propagating in an ideal fluid. The effects of the sound absorption of the materials and sound wave on acoustic radiation force of a multilayered sphere immersed in water are analyzed, with particular emphasis on the shell thickness of every layer, and the width of the Gaussian beam. The results reveal that the existence of particle trapping behavior depends on the choice of the non-dimensional frequency ka, as well as the shell thickness of each layer. This study provides a theoretical basis for the development of acoustical tweezers in a Gaussian standing wave, which may benefit the improvement and development of acoustic control technology, such as trapping, sorting, and assembling a cell, and drug delivery applications.
In recent years, many theoretical and experimental studies have been performed on the acoustic radiation force exerted by a single ultrasonic beam on spherical objects.[1–9] The acoustic tweezers based on acoustic radiation force have become a well-known technique for trapping, sorting, and assembling microparticles (guiding and trapping minuscule particles).[4–13] In particular, in cellular and molecular biology, particle manipulation has been crucial in studying biomechanical properties of various cells and molecules. However, most of these particles mentioned in previous papers are single-layered spherical shell structures. In biomedical engineering and materials science, there are many particles with multiple-layered structures, for example, nanoparticle drugs and cells. In drug delivery applications,[14–17] using acoustic radiation can effectively manipulate polymer microspheres filled with liquid drugs, such that the shell is accurately broken and the drugs can be used in affected areas. A common cell is typically a multilayered tissue that contains a cell membrane, cytoplasm, and a cell nucleus. The acoustic properties of these layers are different; therefore, the study of acoustic radiation force on multilayered spherical shell structures has practical value for applications.
An acoustic standing field can be useful in microfluidic lab-on-a-chip applications, and researchers have calculated the radiation force function for plane and Bessel standing waves.[18–24] A Gaussian standing beam has been used to develop acoustic tweezers that can immobilize latex particles and frog eggs in a fixed position.[25] In this paper, we present a model to calculate the acoustic radiation force by a Gaussian standing wave upon a spherically symmetric multilayered sphere based on previous research.[11,26,27] Examples for the radiation force on two- and three-layered spheres with isotropic properties in each layer are studied for the radius ratio of different layered materials. This study shows that the theory developed in this paper provides a theoretical basis for multilayered spherical particle manipulation.
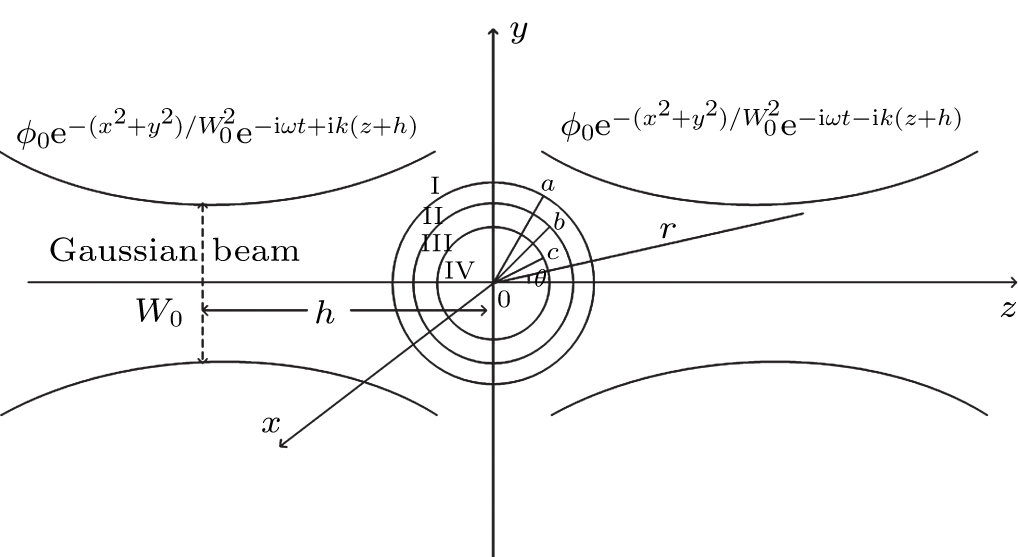
Let a Gaussian standing wave be incident upon a three-layered sphere immersed in an inviscid fluid medium, with the wave propagating along the + z direction. The origin of coordinates of the spherical coordinate system is shown in Fig.
For simplicity, it is assumed that the Gaussian beam is weakly focused. Moreover, the phase front of propagation of the Gaussian beam is almost equal to the plane wave near the beam waist. This means that it can be approximately regarded as an acoustic wave with Gaussian amplitude distribution in that region. Assume also a homogeneous and isotropic fluid of infinite extent with adiabatic speed of sound c1 and density 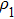
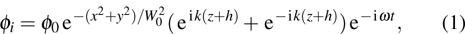 |
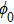
Let 
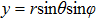
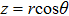


In a spherical coordinate system, the velocity potential of an incident wave can be expressed in terms of a general eigenfunction expansion of the form[8,18]
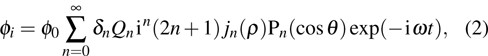 |
 |
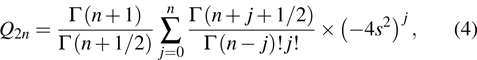 |
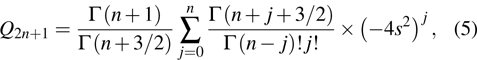 |

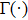
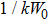
To validate the finite series method, the incident Gaussian beam has been calculated by exact solution as well as a finite series solution for different beam widths.[4] The results show that when 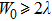
The Gaussian standing wave with wavelength 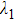
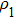
The scattered velocity potential can be expressed as
 |
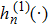
 |
The particle vector displacement Ui (i = 2, 3, 4) in the shell of the elastic material is assumed to be[2,3]
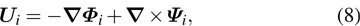 |
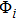
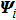
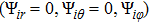
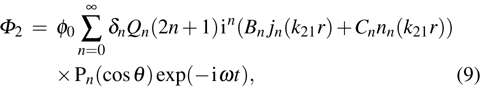 |
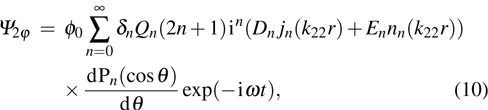 |
 |
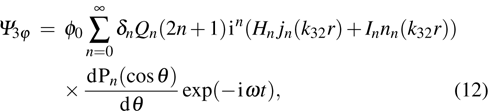 |
 |
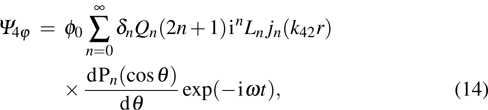 |

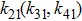
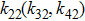
The boundary conditions lead to 11 linear equations. After laborious but straightforward calculations, the scattering coefficient An is determined in the following form:
The acoustic radiation force 
 |
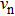
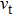
After calculation, 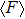
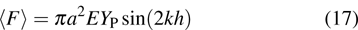 |
 |
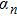
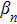
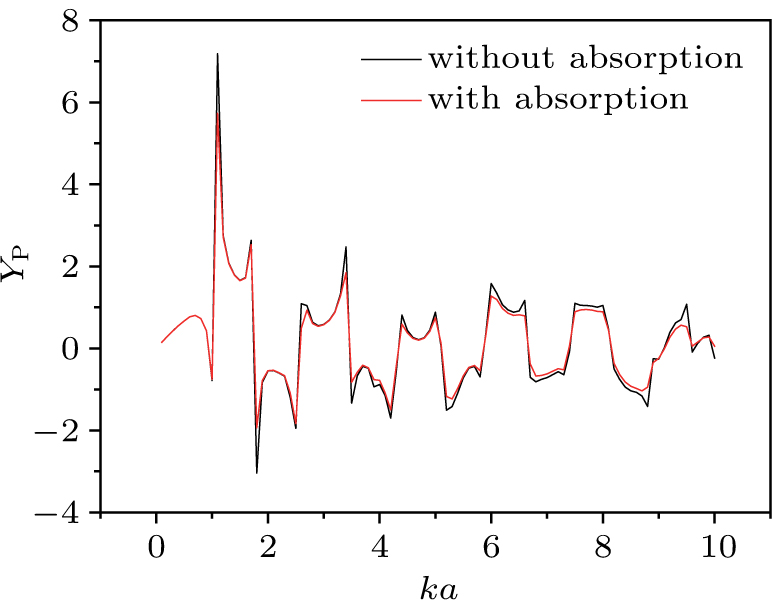
The acoustic radiation force function YP given by Eq. (
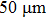
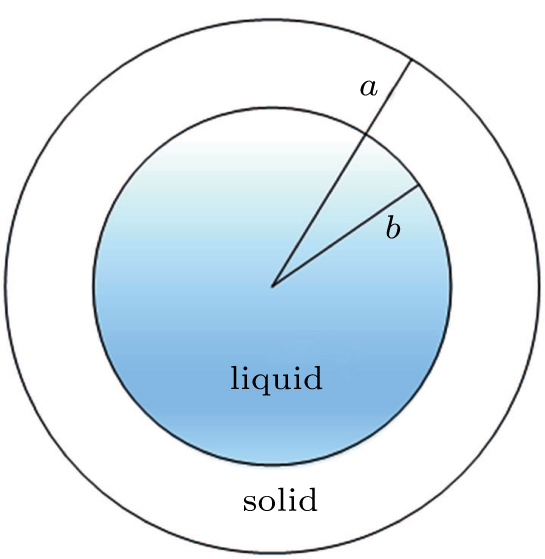
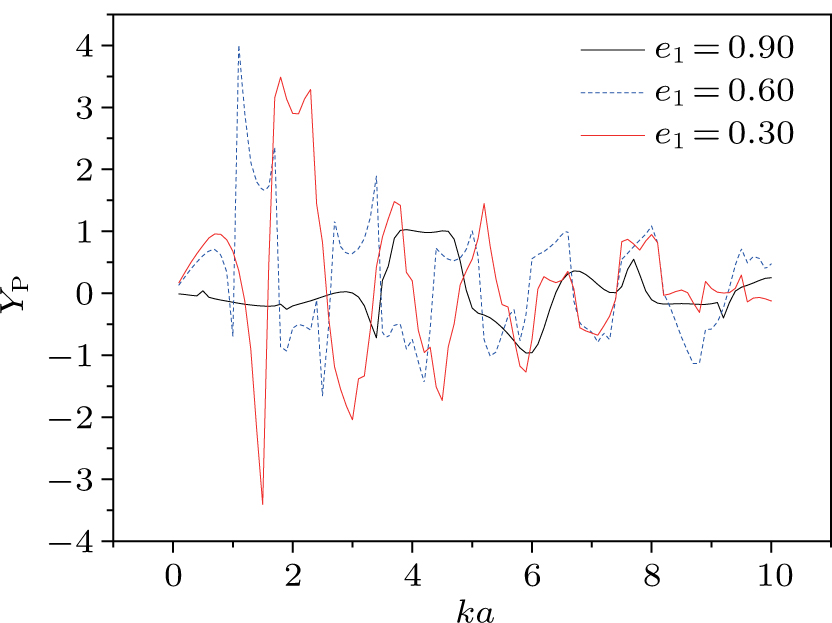
The acoustic radiation force acting on a fluid drug coated by a spherical polymer-type layer can be used for drug delivery applications in which the shell is accurately broken and the drug is used in the affected areas. The plots of axial radiation forces in a two-layered model (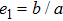
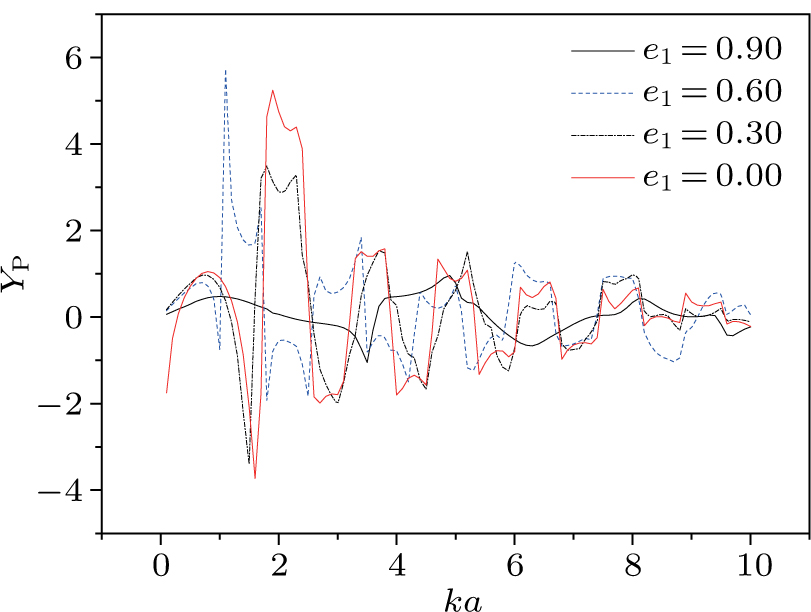 | Fig. 4. (color online) Acoustic radiation force function vs. ka for the two-layered sphere filled with water with different e1. |
Figure 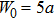
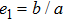
In addition, with a large difference on acoustic impedance between the PMMA shell and the surrounding medium (water), the particle suffers larger radiation force when 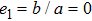
Figure 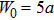
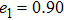
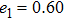
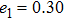
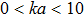
 | Fig. 5. (color online) Acoustic radiation force function vs. ka for the two-layered sphere filled with animal oil with different e1. |
Figures 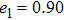
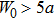
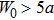
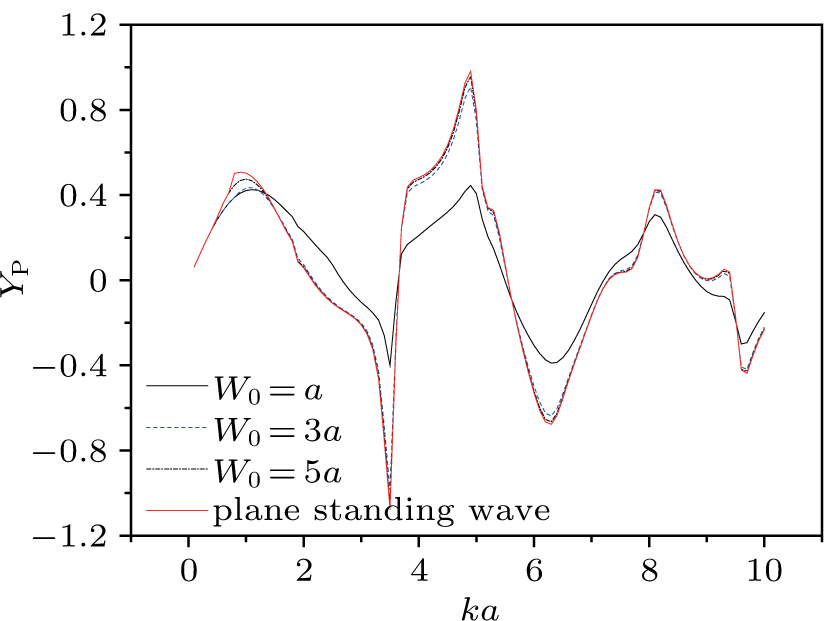 | Fig. 6. (color online) Acoustic radiation force function vs. ka for the two-layered sphere filled with water with different W0. |
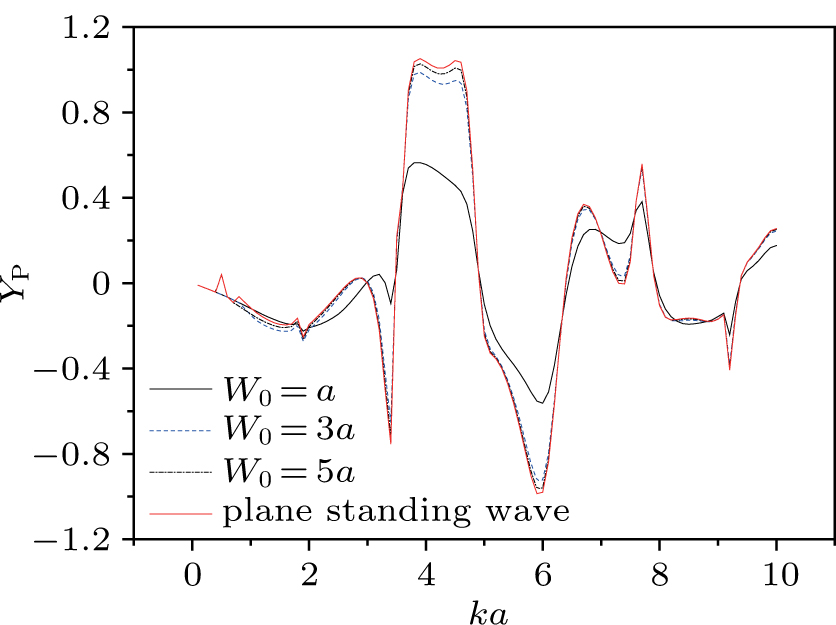 | Fig. 7. (color online) Acoustic radiation force function vs. ka for the two-layered sphere filled with animal oil with different W0. |
Figure
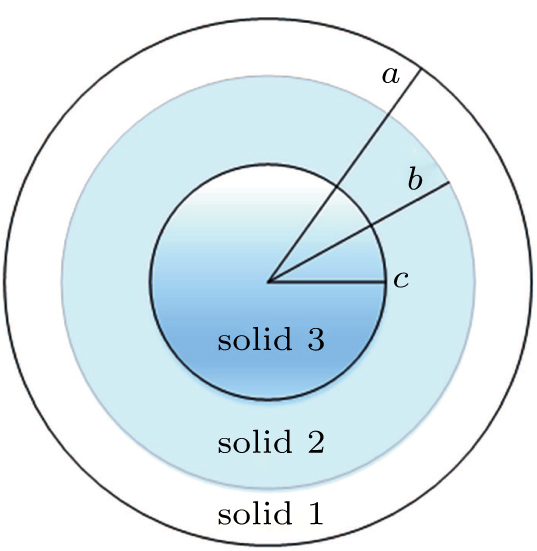
Relative to the single-layered and two-layered spherical structures, many biological tissues have a three-layered spherical structure. Hence, the study of acoustic radiation force on three-layered spherical shell structures has more practical value for applications. Figures
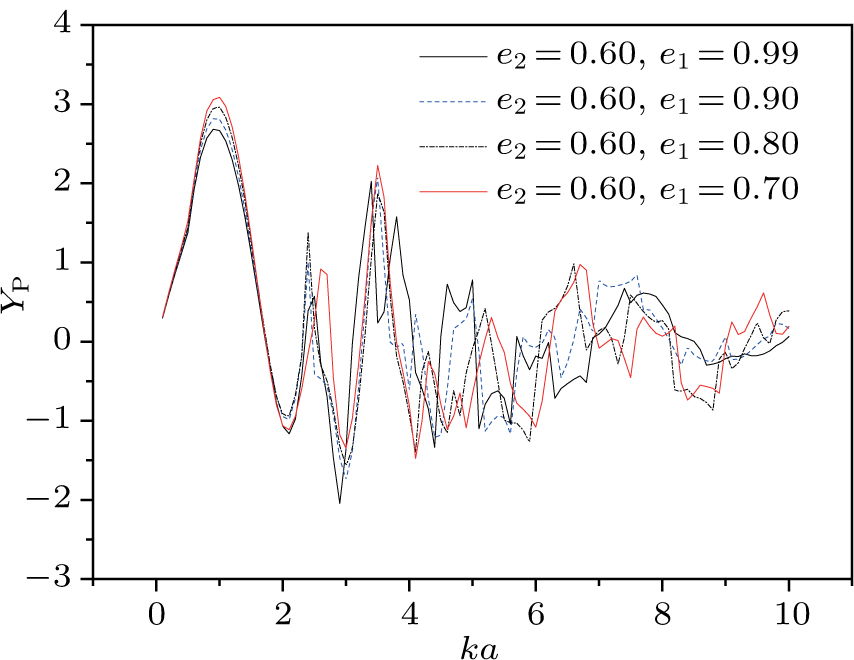 | Fig. 9. (color online) Acoustic radiation force function vs. ka for a three-layered sphere with different e1. |
In Fig. 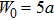
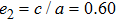
Figure 
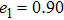
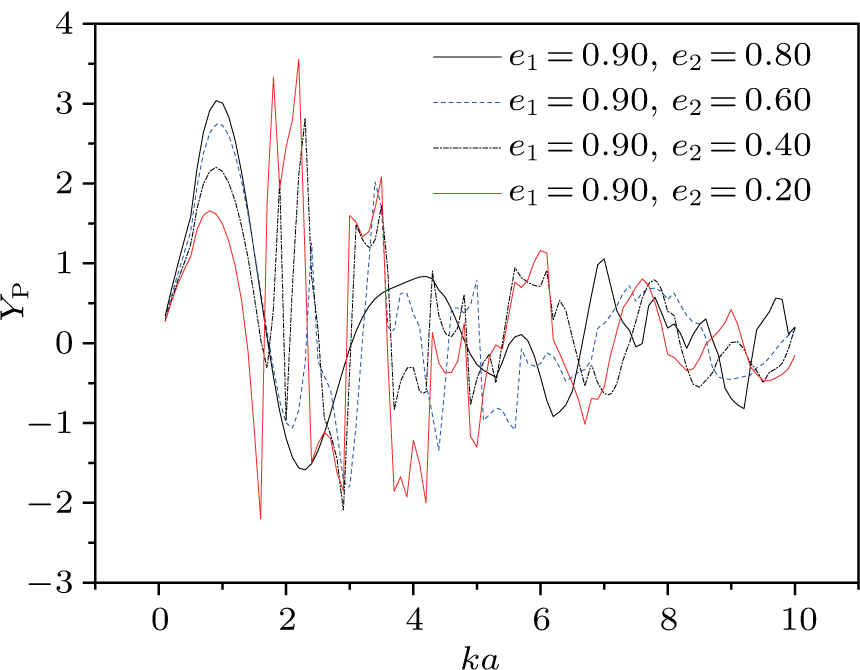 | Fig. 10. (color online) Acoustic radiation force function vs. ka for the three-layered sphere with different e2. |
Figure 
Based on the finite series method, the Gaussian standing wave using spherical harmonic functions and the beam coefficients of the Gaussian beam are observed. The acoustic radiation force function can be obtained for a multilayered spherical particle in fluid using the Gaussian standing wave acoustic field. The numerical analyses for two- and three-layered spherical shells are performed with a particular emphasis on the effects of the ratio of outer radius to inner radius of the shell on the acoustic radiation force. We also discuss the influence of the width of the Gaussian wave on the radiation force function. The results show that the acoustic radiation force is negative at some ka values, generating a potential well. This suggests the possibility of using Gaussian standing waves to manipulate multilayered spheres with known mechanical and acoustical properties, providing an impetus for further research on cell biomechanics and drug delivery. However, if further progress can be made in the structure of a cell and drug carrier microsphere, such as the acoustical properties of cell components, more valuable and meaningful results can be obtained based on the theory presented in this paper.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |