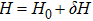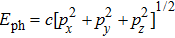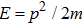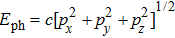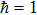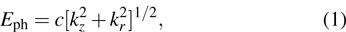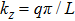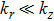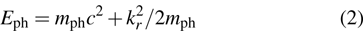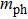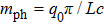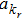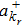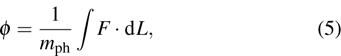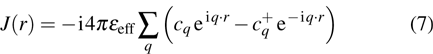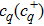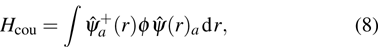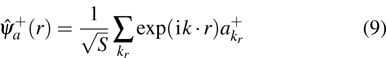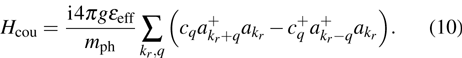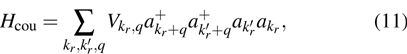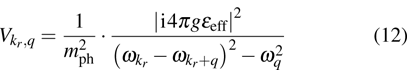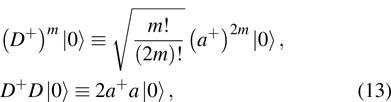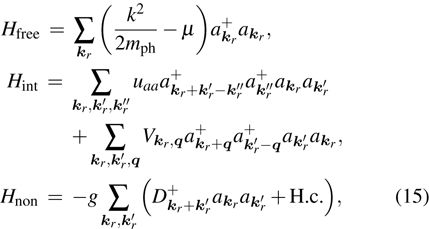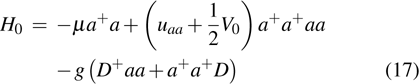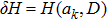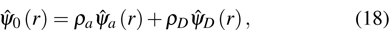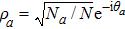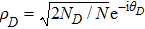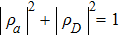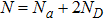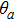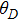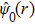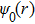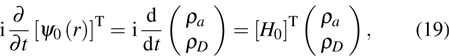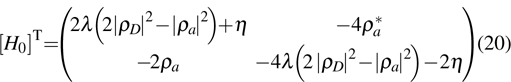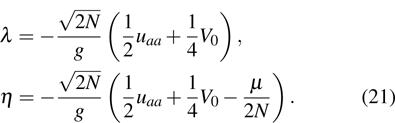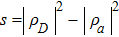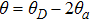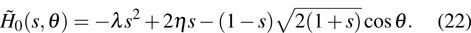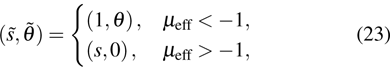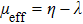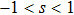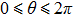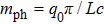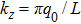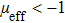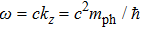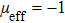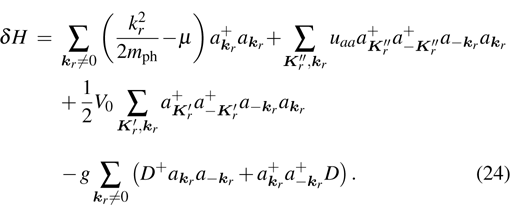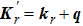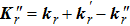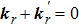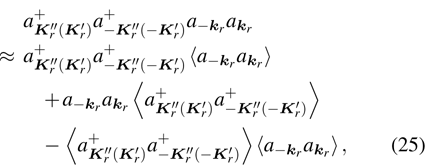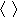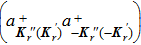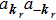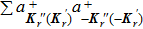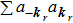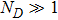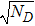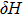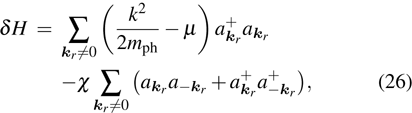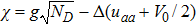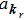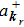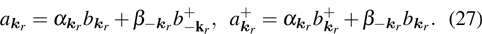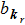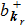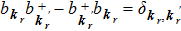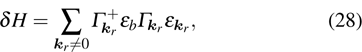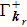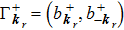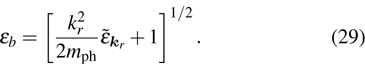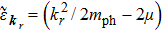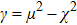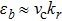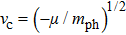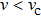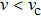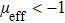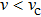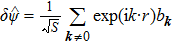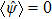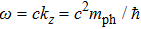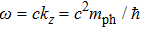School of Physics and Information Science, Shanxi Normal University, Linfen 041004, China
† Corresponding author. E-mail:
jjzhangphys@163.com
1. IntroductionIn the past few decades, considerable attention has been paid to the research of quantum nonlinear processes.[1–5] In quantum optics, numerous nonlinear processes are analyzed starting from high harmonic generation, especially the second harmonic generation (SHG). In the process of SHG, two photons with frequency ω interact in an optically nonlinear medium to create a second-harmonic photon with frequency 2ω. In recent years, considerable efforts[6–11] have been made to obtain enhanced harmonic generation. It seems that we have already obtained enough information in the field of SHG. Recent progress in Bose–Einstein condensation (BEC)[12–14] of photons has opened a new pathway for obtaining enhanced harmonic generation.
The phenomenon of BEC was first proposed by Einstein in 1924, who showed that a noninteracting bosonic gas can undergo a phase transition below a critical temperature to macroscopically populate the ground state. In recent years, the BEC-like phase transition has been observed in several physical systems,[15–20] including atomic gas, exciton polaritions, solid-state quasiparticles, and so on. It is well known that essentially the laser beam or electromagnetic field can be considered as a boson system consisting of photons. Since the phenomenon of BEC is a common property of bosonic systems, one wonders whether it is possible to have a BEC of photons. For the most ubiquitous black-body radiation, owing to the vanishing chemical potential, the photon number of a black-body is not conserved, thus it is not possible to obtain this kind of condensation. However, as shown by Chiao,[21] the situation is different for the two-dimensional optical system, in which it could be possible to realize the BEC of photons. Number-conserving photon gas was first observed experimentally by Klaers et al. in a two-dimensional optical microcavity.[12] Soon after, the BEC of photon gas was realized.[13] Recently, due attention is paid to the novel nonlinear phenomenon of photons.[22–31]
In this paper, we construct a system inside a two-dimensional nonlinear micro-cavity which provides a confining potential, a chemical potential, and an effective mass for the photon. In the process of SHG, two massive photons can couple with each other to form a photon-pair. It should be pointed out that here the photon-pair is very similar to the diatomic molecule in the Feshbach resonance model.[32,33] Furthermore, the investigation of the enhanced harmonic generation is carried out under the background of the BEC of the mixed system. In the condensate phase, the model Hamiltonian can be divided into two parts
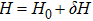, where H0 is the condensate mode, and δH is the perturbation mode. Further investigations show that the quantum phase transition and the elementary excitation of the system in different quantum modes are all related to the harmonic generation. In order to describe the phenomenon, a new quantum phase, the harmonics phase, is introduced. We also give the order parameter of the new physical phase.
The paper is organized as follows. In Section 2, the effective mass of the photon is introduced, and then the self-interaction and the couple-interaction between photons are investigated respectively. In Section 3, we establish the BEC model of the mixed system and analyze the quantum phase transition of the condensate mode. In Section 4, we investigate the elementary excitation of the perturbation mode. We also introduce the harmonics phase to describe the enhanced second harmonic generation. A comprehensive discussion and summary is given in Section 5.
2. Model and Hamiltonian2.1. Effective photon massWe all know that usually photon has no rest mass and its physical properties are described by the free-photon dispersion relation
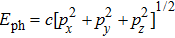. Obviously, it is different from the usual mass–energy relation
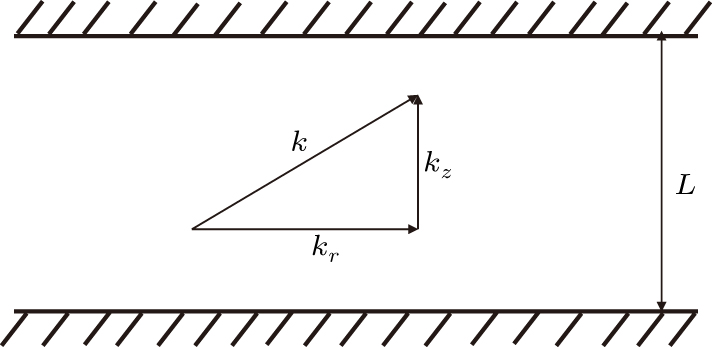
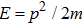for bosons with non-zero rest mass. In quantum theory, the difference between the photon and the other bosons is considered to be the main reason for the black-body radiation phenomenon by Planck. The phenomenon implies that the macroscopic condensate of photons at the zero-momentum state is impossible. Fortunately, the physics in two-dimensional (2D) systems is drastically different from that in higher-dimensional systems. The 2D character makes the problem simple enough that some special effects can be observed. In the case of photons confined inside a two-dimensional optical cavity as shown in Fig. 1, owing to the high-reflectivity, the cavity will impose a quantization condition on the allowed values of the longitudinal momenta pz of the photons. As a result, in the two-dimensional optical micro-cavity, the usual dispersion relation (
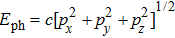) changes to (with
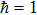in this paper)
 | |
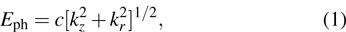where
kr is the transversal wavenumber of the photon and the longitudinal wavenumber
kz is given by the quantization condition
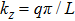
. Here,
q is an integer and
L is the longitudinal distance between the mirrors. Furthermore, for fixed longitudinal mode number
q0 and in paraxial approximation (
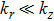
), a new dispersion relation
can be obtained from the Taylor expansion of Eq. (
1). Above, a new physical quantity
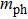
with the relation
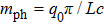
is introduced and it is identified as the effective mass of the photon. Here, it is convenient to redefine the zero of energy, so that the photon in the micro-cavity is formally equivalent to a general boson moving in the transverse resonator plane with the effective kinetic energy
The non-vanishing effective mass of photon here implies that in the two-dimensional optical micro-cacity, there also exists a macroscopic condensate of photons in the zero transversal momentum state.
2.2. Interaction between the photonsIt is well known that the interaction between photons is always ignored in the free space. However, in the current model, the electromagnetic field is confined by the micro-cavity which will conduce to the self-couple of electromagnetic waves of various frequencies. The result is that here the interaction between photons should also be considered. According to the standard process of second quantization, the self-interaction between photons can be written in the form
in the weakly-interaction approximation. In the above expression, the parameter
uaa represents the two-body potential and
(
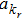
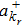
) is introduced as the annihilation (creation) operator of massive photons with different transversal wave-vectors.
In addition, in the current model we assume that the micro-cavity is filled with a medium exhibiting significant second-order nonlinearity. Thus, for the complete description of photons, we should also investigate the interaction between the electromagnetic field and the nonlinear medium in the two-dimensional optical micro-cavity. The typical description of the interaction is polaritons or resonance between the electromagnetic field and the polarization field of the medium. However, owing to the non-vanishing effective mass of photons, the polaritons and resonance will be inhibited in the two-dimensional model and there exists a balance between the two kinds of fields in the longitudinal direction. Therefore, we only need to consider the interaction in the transversal mode. In this direction, the massive photon is very similar to the general electron whose move will cause the deformation of the medium. The deformation will further lead a coupling between the photon and the nonlinear medium. Here, we describe the coupling between the massive photon and the polarization field by a coupling potential
 | |
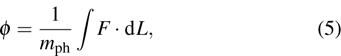where
is the deformation force of photons in the polarization field and
is the microscopic form of the transversal polarization field with
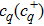
the annihilation (creation) operator of the transversal optical phonons. The parameter
g is explained as the coupling factor and
εeff is the effective dielectric constant. The second quantization form of the coupling potential is
where
is the field operator of photons. Furthermore, by substituting the expression of the coupling potential given by Eq. (
5) into Eq. (
8), we can obtain the following quantum form:
This expression describes the coupling process between the electromagnetic field and the polarization field in the current model. To better understand the process, the standard canonical transformation of Eq. (
10) is also performed,
[34] the result is
where
is the interacting parameter. The result implies that there exists an interaction between the photons by exchanging the transversal optical phonons in the current model. The interaction is determined by Eq. (
12) and it can be attractive for a negative interacting parameter. Here, the attractive interaction between the photons also means the existence of photon-pair, which can be describe by a new operation, namely, the photon-pair creation operation
D+, with the relation
where
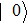
is the vacuum state.
In the current model, we assume that the system will adjust itself to the presence of this attraction and further propose the following phenomenological grand-canonical Hamiltonian H,
with
which gives a simple model of the system of massive photons in the two-dimensional optical micro-cavity. The term
H0 represents the energy of the free photon gas and
μ is the chemical potential. The interaction term
Hint is consisted of two parts, the self-interaction and the coupling-interaction. The non-linear term
Hnon describes the creation and annihilation of photon-pairs.
3. BEC of the systemIn the previous discussion of photons confined inside the two-dimensional optical micro-cavity, we have pointed out the existence of BEC phase of the current system. In the condensate phase, we can separate out the condensate modes from the grand-canonical Hamiltonian and write the Hamiltonian in the form
where
is the condensate part of the Hamiltonian, and
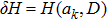
is the perturbation term which will be discussed later. For the current system, the condensate mode is consisted of two components, the photon and photon-pair, and it can be described by the composite field operator
,
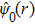
where
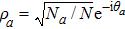
and
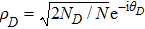
are the probability amplitudes of the two components which satisfy the normalization condition
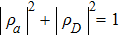
, and
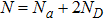
is the total photon number.
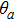
and
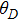
denote the phases of the two species. In the condensate phase, the quantum fluctuation can be ignored and the operator
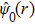
can be replaced by a classical field
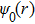
which satisfies the discrete G–P equation
where
is the matrix form of the condensate Hamiltonian with parameters
Mathematically, by introducing the population difference
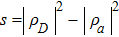
and the relative phase
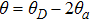
, the nonlinear two-species system described by Eqs. (
17) and (
18) is cast into a classical system with Hamiltonian
In the condensate phase, it is very important to understand the properties of the ground state of the system. By minimizing the energy
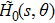
with canonical variables
s and
θ, the optimum values (
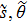
) of the parameters for the ground state can be obtained as
where
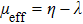
can be explained as the effective chemical potential of the photon gas,
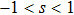
, and
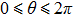
. The result implies the existence of a quantum phase transition from the mixed photon photon-pair condensate phase to the pure photon-pair condensate phase. Furthermore, if we relate the definition of the effective mass of photon,
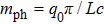
, to the mixed longitudinal wave number
kz with
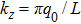
, it can be easily found that the conversion of two attractive photons to a coupling photon-pair can be explained as the generation of second harmonic. Thus, the quantum phase transition here also means that when
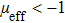
, the electromagnetic wave with frequency
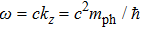
will all convert into the wave of double frequency in the ground state of the mixed photon gas.
4. Elementary excitation of the systemAlthough over the phase point
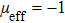we can obtain enhanced second harmonic, in the pure photon-pair condensate phase, another critical factor, the elementary excitation, has also to be considered. The reason is that the elementary excitation is related with the energy loss which also influences the conversion of the second harmonic. The elementary excitation of the system is described by the perturbation Hamiltonian δH,
Above, we have taken
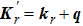
and
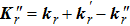
. We have only considered the photon-pairs with opposite wave-vectors, i.e., we have taken
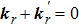
. In the condensate phase, we can use the mean-field approximation
[35] and write the interaction term in the form
where
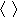
represent the average of the corresponding operators at the ground state. Especially, in the pure photon-pair condensate phase, there exists a balance between the creation
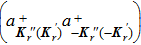
and annihilation (
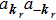
) of the pair operators, which means that we can neglect the difference between
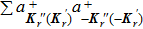
and
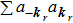
and replace the average value of them by a term
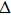
. Furthermore, for the pure photon-pair condensate phase, since
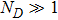
, we can also replace all the occurrences of
D and
D+ by
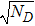
. Finally, in the pure photon-pair condensate phase, we can write the perturbation Hamiltonian
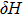
in the simple form
where the parameter
χ is given by
.
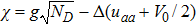
The Hamiltonian is quadratic in the operators
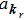and
and 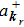can be diagonalized by the Bogoliubov transformation
This transformation introduces a new set of operators,
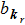
and
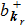
, to which we impose the same Bose commutation relation
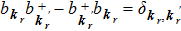
. By virtue of the linear transformation, the Hamiltonian can be finally reduced to the diagonal form
where
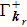
is given by
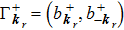
and the set of operators
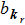
and
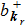
can be explained as the annihilation and creation of quasi-particles with energy
Above,
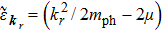
is the effective kinetic energy of the photon. In Eq. (
29), we have also scaled the energy by the parameter
γ, with relation
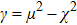
. For small moment, by choosing appropriate zero point energy we can ignore the constant term,
[36] and obtain the following dispersion law of quasi-particles,
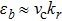
, where
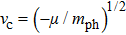
is the critical velocity of photons in the transverse resonator plane. When the velocity of photons satisfies the relation
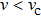
, the elementary excitation of the mixed system can be inhibited and there is no loss of energy during the generation process of second harmonic.
Here the relation
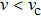also means the existence of a superfluidity phase of the mixed photon gas. In this paper, we also introduce a new phase named the harmonics phase to describe the phase transition and superfluidity of the current system. The harmonics phase is defined by the feature that the mixed photon gas is simultaneously in the pure photon-pair condensate phase and the superfluidity phase, i.e., the mixed system satisfies simultaneously the relations
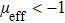and
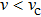. The phase transition of the system from the general phase to the harmonics phase can be denoted by the order parameter
where
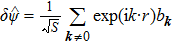
is the field operator of quasi-particles. As
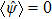
, the system is in the harmonics phase, which means that the electromagnetic wave with frequency
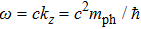
will theoretically all convert into the wave of double frequency in the ground state with zero-loss of energy.
5. ConclusionWe have constructed a two-dimensional BEC model consisting of massive photon and photon-pair. Based on the new nonlinear model, we have reinvestigated the traditional process of the SHG. Further analyses show that in the condensate phase, two different nonlinear effects, the quantum phase transition in the condensate mode and the elementary excitation in the perturbation mode, are both related to the harmonics generation. In this paper, we have also introduced a new quantum phase named the harmonics phase to describe the enhanced harmonic generation. Theoretically in the harmonics phase, the electromagnetic wave with frequency
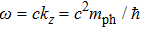will all convert into the wave of double frequency with zero-loss of energy.
