Cite this Article
Li Quan-Quan, Xu Xue-Mei, Yin Lin-Zi, Ding Yi-Peng, Ding Jia-Feng, Sun Ke-Hui. Implication of two-coupled tri-stable stochastic resonance in weak signal detection. Chinese Physics B, 2018, 27(3): 034203  
Permissions
Implication of two-coupled tri-stable stochastic resonance in weak signal detection
Li Quan-Quan, Xu Xue-Mei †, Yin Lin-Zi, Ding Yi-Peng, Ding Jia-Feng, Sun Ke-Hui
School of Physics and Electronics, Central South University, Changsha 410083, China

 

† Corresponding author. E-mail: xuxuemei999@126.com

Abstract
Abstract

Stochastic resonance (SR) has been proved to be an effective approach to extract weak signals overwhelmed in noise. However, the detection effect of current SR models is still unsatisfactory. Here, a coupled tri-stable stochastic resonance (CTSSR) model is proposed to further increase the output signal-to-noise ratio (SNR) and improve the detection effect of SR. The effects of parameters a, b, c, and r in the proposed resonance system on the SNR are studied, by which we determine a set of parameters that is relatively optimal to implement a comparison with other classical SR models. Numerical experiment results indicate that this proposed model performs better in weak signal detection applications than the classical ones with merits of higher output SNR and better anti-noise capability.

PACS: 42.30.Rx;42.55.Px;42.79.-e;42.87.-d
Keyword:stochastic resonance;extracting weak signals;signal-to-noise ratio (SNR);detection effect
1. Introduction

Owing to an increasing demand for detecting weak signals in many fields, weak character signal detection technology has gradually become a hot research topic. While traditional methods were limited to expensive devices and relatively low signal-to-noise ratio (SNR), researchers have devoted themselves to seeking another way of measuring weak character signals in strong noise. Since firstly discovered by Benzi et al. in 1981 as an explanation for the observed periodicity in the ice ages on earth,[1] stochastic resonance (SR) has attracted much attention due to its most distinct merit of enhancing the weak signal by exploiting the noise energy. During the past few decades, SR has been explored experimentally in a large variety of fields, such as physics, biology, optical systems, and large mechanical fault diagnosis.[2–6]

The cooperative effect of noise, the periodic driving in a bi-stable system, and the application of the SR system for detecting a weak signal accompanied with heavy background noise were investigated by Jung in 1991.[7] Signal amplification in a nano-mechanical Duffing resonator via SR was proposed by Gammaitoni in 1995.[8] Lutz applied SR in nonlinear signal detection in 2001.[9] Gandhimathi and Mankin studied the condition for noise energy induced signal energy to enhance weak signal detection performance.[10,11] Saikia presented a modified adaptive SR model to detect faint signals with strong noise in sensors.[12] Some other researchers discussed the issues on coupling in SR models.[13–19] Besides, SR systems with many new potential functions, like the tri-stable potential, were also explored by researchers.[20–22]

However, for these existing SR models, the output SNR is not high enough and the detection effect is still not satisfactory. The detection effect of SR refers to the noise utilization or the enhancement extent on the periodic input signals, whose evaluation index is mainly the SNR or SNRgain of the system response tracking periodic input signal in this study. In other words, the greater the noise utilization or the enhancement extent on the periodic input signals, the greater SNR or SNRgain of the system response is, and vice versa. Thus, it is necessary to search new resonance models to further improve the capability of utilizing the noise to enhance the input signal through the application of SR. Based on the studies of predecessors and by combining the coupling and tri-stable potential function, a novel coupled tri-stable stochastic resonance (CTSSR) model is proposed in this paper to improve the output SNR and detecting performance of SR systems.

This paper is organized as follows. In the next section, the principle of tri-stable stochastic resonance (TSR) is described. Then we propose our novel model and analyze the effects of the system parameters on the output SNR. In Section 3, by comparing this new system with some other existing SR models in the aspects of SNR and time-frequency domain, we prove the merits of CTSSR compared to the conventional SR models. The last section is devoted to the conclusion.

2. CTSSR
2.1. Tri-stable stochastic resonance model

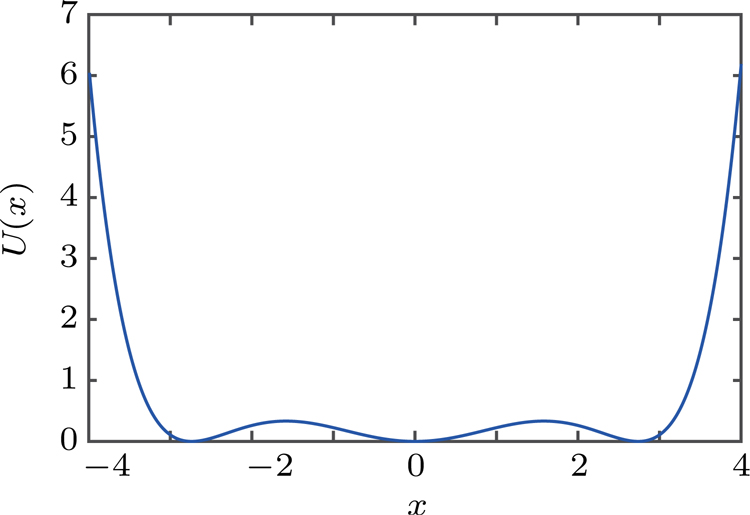
The basis of the tri-stable SR phenomenon can be described as follows. A particle is driven by a weak periodic signal and the Gaussian white noise in a tri-stable potential containing three potential wells and two potential barriers. The periodic oscillation can be enhanced when the noise is at a suitable level, which can be explained by the equation[22]

where with represents the noise term, in which D denotes the noise intensity and ξ (t) depicts the Gaussian white noise with zero mean and unit variance; is a periodic signal, in which A is the amplitude, with being the driving frequency, and ϕ is the phase.

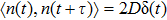
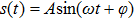
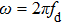
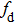
For the TSR model, U(x) represents a potential function

where a, b, and c denote the parameters of the tri-stable potential that owes three wells and two barriers as shown in Fig. 1.

Fig. 1. (color online) The tri-stable potential function U(x) in CTSSR model.
2.2. CTSSR model

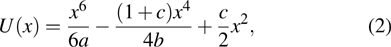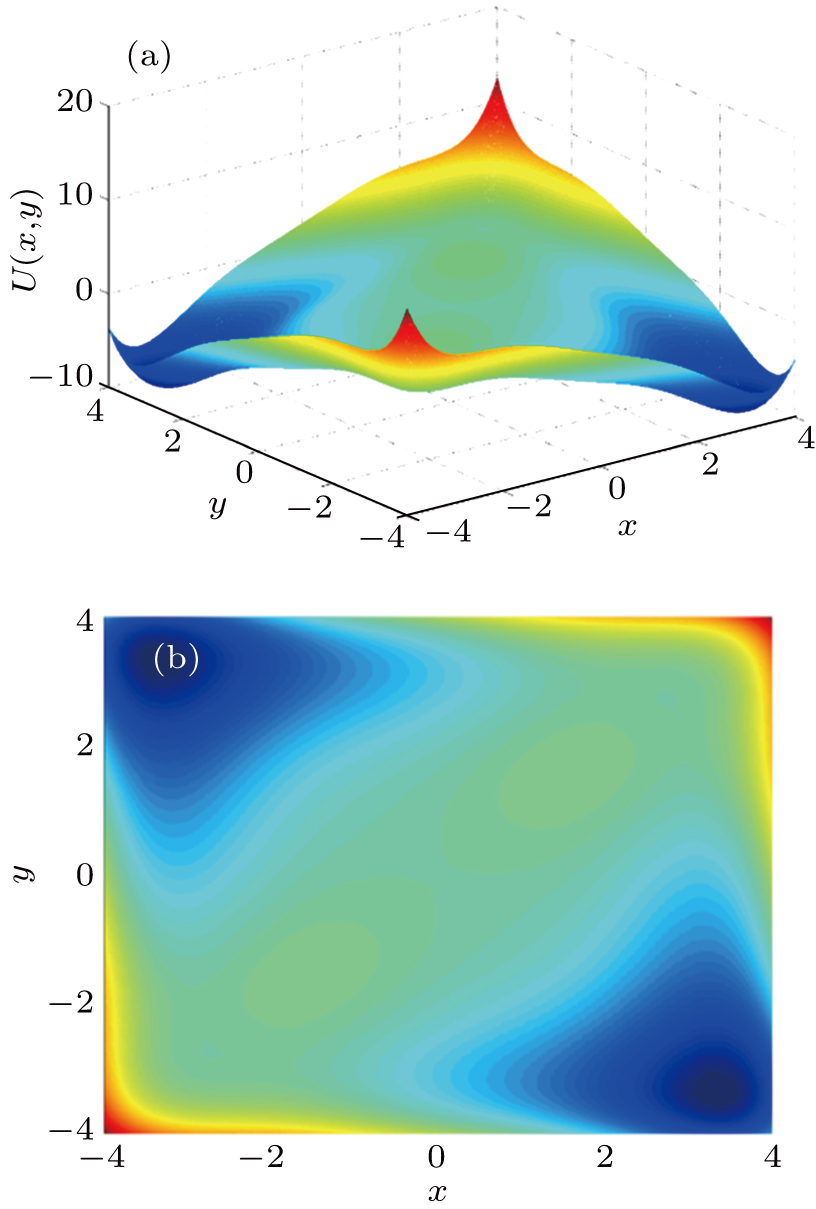
Although the output SNR is improved by using the method of tri-stable resonance, it is still not satisfactory. When the intensity of noise becomes high, the detecting performance will be poor. In order to obtain higher SNR and excellent performance, based on the traditional TSR model, we propose a novel model, CTSSR, which can be illustrated as follows:

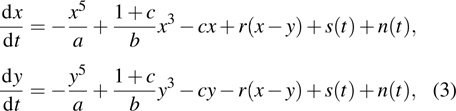where the first equation represents the controlled subsystem, the second equation shows the controlling subsystem, r is the coupling coefficient, while s(t) and n(t) depict the original sinusoidal signal and the additional white Gaussian noise, respectively.

Under this circumstance, the potential function evolves into a new form

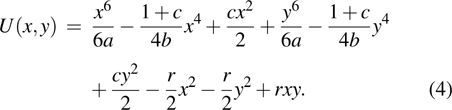Comparing Eq. (2) with Eq. (4), we can obviously observe that the dynamic behavior of the potential function in CTSSR, as illustrated in Fig. 2, is much more complicated than the classic one. As a result, our proposed model has ensemble priority compared to the traditional SR models in nature.

Fig. 2. (color online) The potential function of CTSSR: (a) front view, (b) top view.
2.3. Numerical implementation of CTSSR

In order to meet the demand for application in practical engineering, we need to convert the continuous system into a discrete form for convenience and high efficiency. We utilize the fourth-order Runge–Kutta (RK4) algorithm to implement the discretization of the continuous system. By selecting a calculation step h, according to Eq. (3), the output discrete time series x[n] and y[n) can be calculated as follows:

where x[n] is selected as the output series to perform the subsequent calculations, one of which is the signal-to-noise of the output signal, SNRout. By calculating the power spectrum of discrete x[n] via fast Fourier transform (FFT), SNRout can be obtained as
where N denotes the length of the time series, depicts the power of the driving frequency in the calculated spectrum, and the item Ai represents the total power of noise. Furthermore, to more effectively and clearly evaluate the performance of the system, unlike the traditional definition, i.e., the ratio of SNRout to SNRin, SNRgain is defined in a new form to judge the system’s performance in another way, whose expression is
where SNRin means the signal-to-noise of the input noise signal, and Psout, Pnout, Psin, Pnin represent the power of output useful signal, output noise, input useful signal, and input noise, respectively. Based on this definition, we can determine whether the input useful signal has been strengthened according to the value of SNRgain (positive or negative), instead of numerical comparison with 1. Besides, from the formula, we can see that this measure index indicates a comparison of relative intensity of the useful signal component between the original noise signal and the output signal processed by the CTSSR system.

2.4. The effects of the system parameters

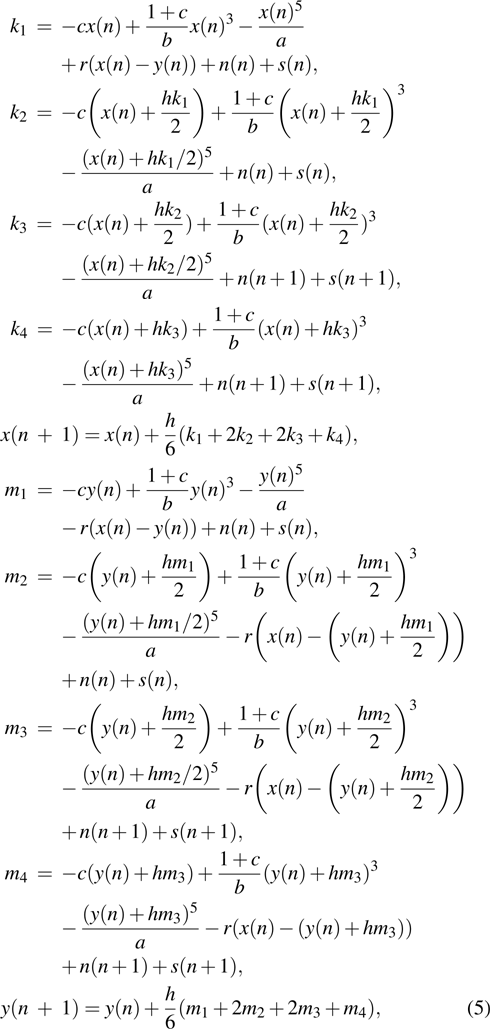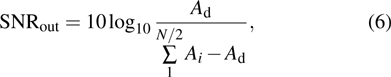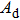
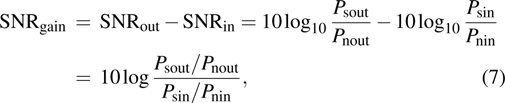In this study, the intensity of the input useful signal is constant, so when the noise intensity increases, SNRin will decrease, and SNRout and SNRgain will vary accordingly. Then an optimal noise intensity in this system corresponds to an optimal SNRin, leading to the highest SNRgain which obviously signifies the occurrence of stochastic resonance. Herein, with a view to the definition of SNRgain and analyzing the SR models from the point of view of SNR thoroughly, we focus on the changes of SNRgain with SNRin to evaluate the performance of the SR models. Besides, the four parameters in the CTSSR system would have an impact on the system’s performance and are variable at the same time. It is extremely hard to seek out a set of optimal parameters. Thus, we adopt the single variable method to investigate the influence of each parameter on the system SNRgain, by which we select a set of parameters that are relatively optimal to conduct the weak signal detection. In our numerical simulation, the amplitude of sinusoidal signal A is 0.3 A, the driving frequency f is 0.01 Hz, the initial phase is 0°, sampling frequency is 10 Hz, and step size h equals to 1/fs.

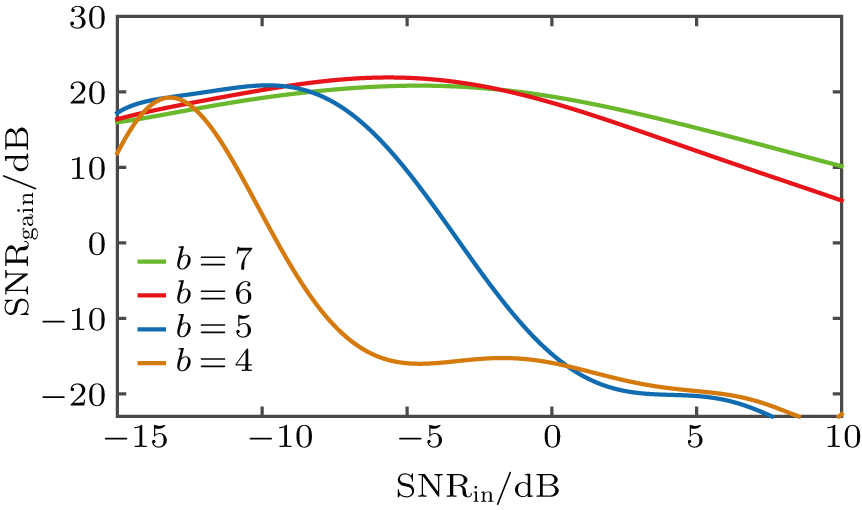Firstly, we explore the effects of the parameter b. SNRgain as a function of SNR of the input signal with noise with different system parameter b and a = 25, c = 0.5, r = 0.5 is shown in Fig. 3. Herein, the values of SNRgain are the averages of the repeated 100 calculations. It is illustrated evidently that the peak shifts to the right and the SNRgain under strong background noise decreases when b increases. Besides, when b = 4 or 5, although SNRgain under strong background noise is relatively high, it is low when . Considering this factor, we set b = 6 to conduct the following studies.

Fig. 3. (color online) SNRgain as a function of SNRin of input noise signal with different system parameter b and a = 25, c = 0.5, r = 0.5.

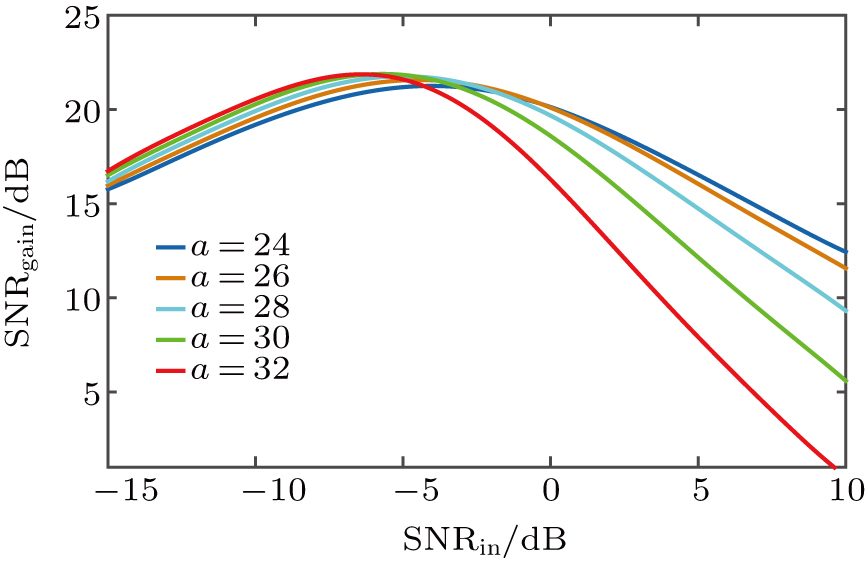Then, the simulation experiment aiming to study the parameter a is performed, as shown in Fig. 4. As we can observe, with the increase of a, the position of the peak shifts to the right and the SNRgain under the strong noise environment increases, which is opposite to the trend with b. So a higher value of a is more suitable for weak signal detection under strong noise. However, there is still a problem we need to take into account: the ability of detecting a weak signal under relatively weak noise will fall rapidly when the value of a is too high. Hence we fix a = 30 to explore the effects of parameter c.

Fig. 4. (color online) SNRgain as a function of SNRin with different system parameter a and b = 6, c = 0.5, r = 0.5.

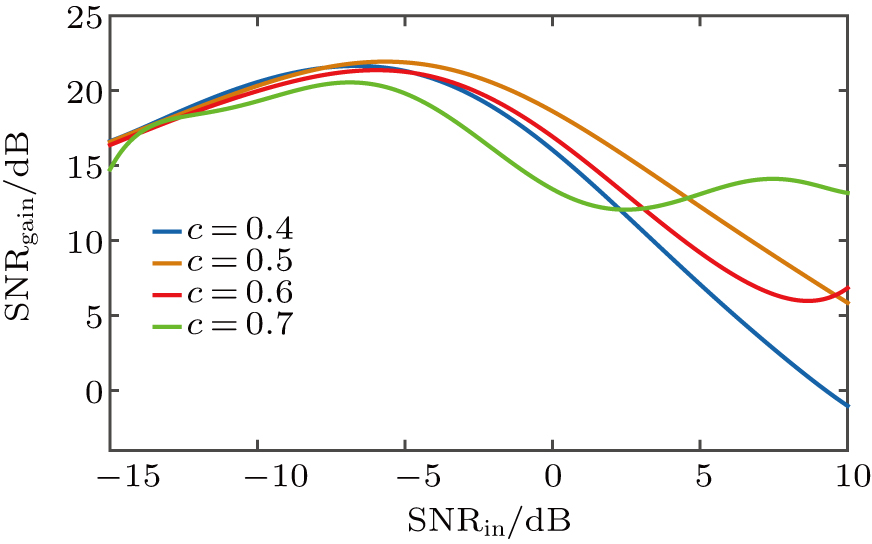Figure 5 shows the SNR versus SNRin with different system parameter c. After an in-depth analysis, it can be concluded that the influence of parameter c on the SNR under strong noise is so faint that we ought to concentrate on the value of SNR under a relatively weak noise environment to select a relatively optimal value of parameter c. Hence, in view of the higher SNR among the range of (−5, 0) of SNRin, we fix c = 0.5.

Fig. 5. (color online) SNRgain as a function of SNRin with different system parameter c and a = 30, b = 6, r = 0.5.

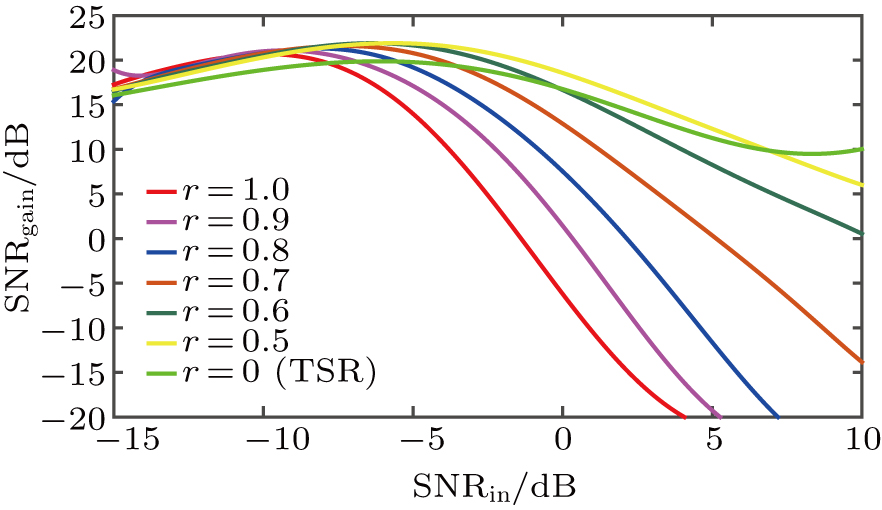
At last, we focus on the effects of r on system SNRgain, which is shown in Fig. 6. From Fig. 6, we draw the conclusion that the position of the peak really shifts to the right when r increases, indicating that the system with a higher value of r has a higher SNR under stronger noise. Thus we can choose a suitable value of r according to the intensity of the background noise to meet our needs. However, the noise intensity is usually high in an actual situation and the performance under strong noise is usually concerned. Therefore, the value of r should be high. Then we select several different relatively high values of r to conduct a thorough study on it, as illustrated in Fig. 7.

Fig. 6. (color online) SNRgain as a function of SNRin with different system parameter r with a = 30, b = 6, c = 0.5 of CTSSR.
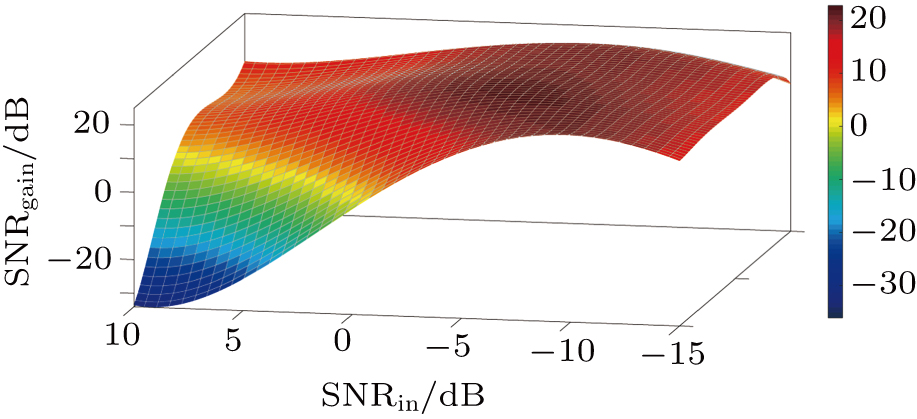
Fig. 7. (color online) SNRgain as a function of SNRin with different r.

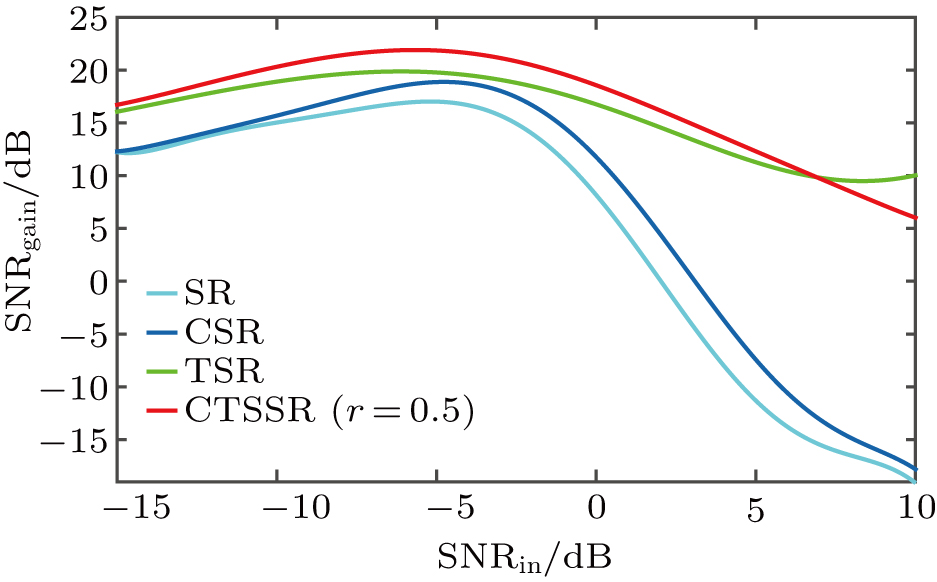
From Fig. 7, we unexpectedly find that it is not true that the higher the value of r, the better the performance of the system is. The peak really shifts to the left when r increases, but there is a problem that the system with a too high r would perform badly in detecting range. It is worth mentioning that the system performs very well synthetically when r equals to 0.5. Accordingly, we choose this value finally to construct a relatively optimal system. As a result, the values of parameters a, b, c, and r have been determined to carry out weak character signal detection.

3. Comparison with other SR models

In order to prove the superiority of the CTSSR, we adopt the above parameters to conduct simulation experiments to compare it with other existing SR models, including bistable SR (SR) (a = 1 and b = 1, it is widely considered as a set of empirical values in the field of stochastic resonance which can induce excellent performance of the system), coupled bistable SR (CSR) (with four variable parameters a, b, r, and SNRin, it is difficult to seek out optimal values of the parameters in the system, and there are no studies which have ever discussed this. Accordingly, we intend to seek out an optimal value of r on the basis of keeping a = 1 and b = 1 and then make the comparison. 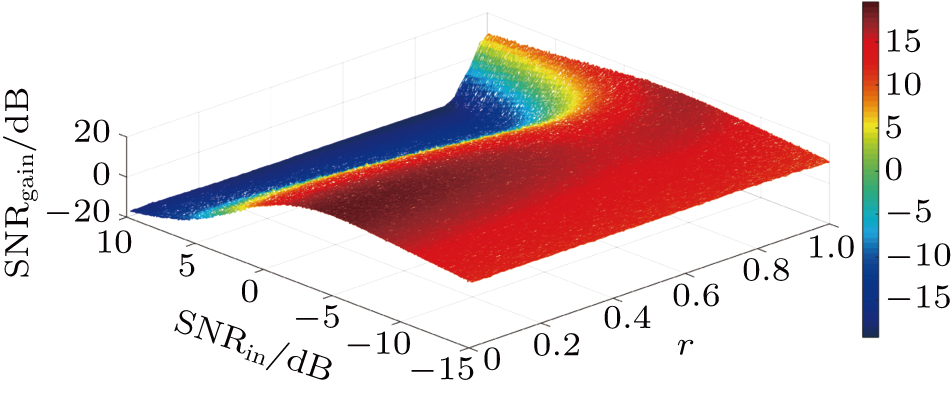Finally, r is determined as 0.25 in consideration of maximum SNRgain and range within which the system has excellent performance ( ), as shown in Fig. 8), and TSR (comparison with TSR is implemented under the condition that the two systems’ parameters a, b, and c are the same, by which we mean to explore the effects of r). At first, we make the comparison in the aspect of SNRgain, as illuminated in Fig. 9.

Fig. 8. (color online) SNRgain as a function of SNRin with different system parameter r with a = 1, b = 1 of CSR.
Fig. 9. (color online) SNRgain as a function of SNRin of different systems.

The superiority of CTSSR (r = 0.5) in contrast to other SR models is obvious and significant. Among almost all the range of SNRin, the SNRgain of CTSSR is the highest, indicating that the CTSSR has not only an excellent performance in improving the SNR in weak signal detection, especially under the strong noise environment, but also a better performance in detecting range. In other words, the SNR of the CTSSR system could maintain high in a wider range. Besides, we can observe that the ranking by performance in SNR from high to low is: CTSSR, TSR, CSR, and SR.

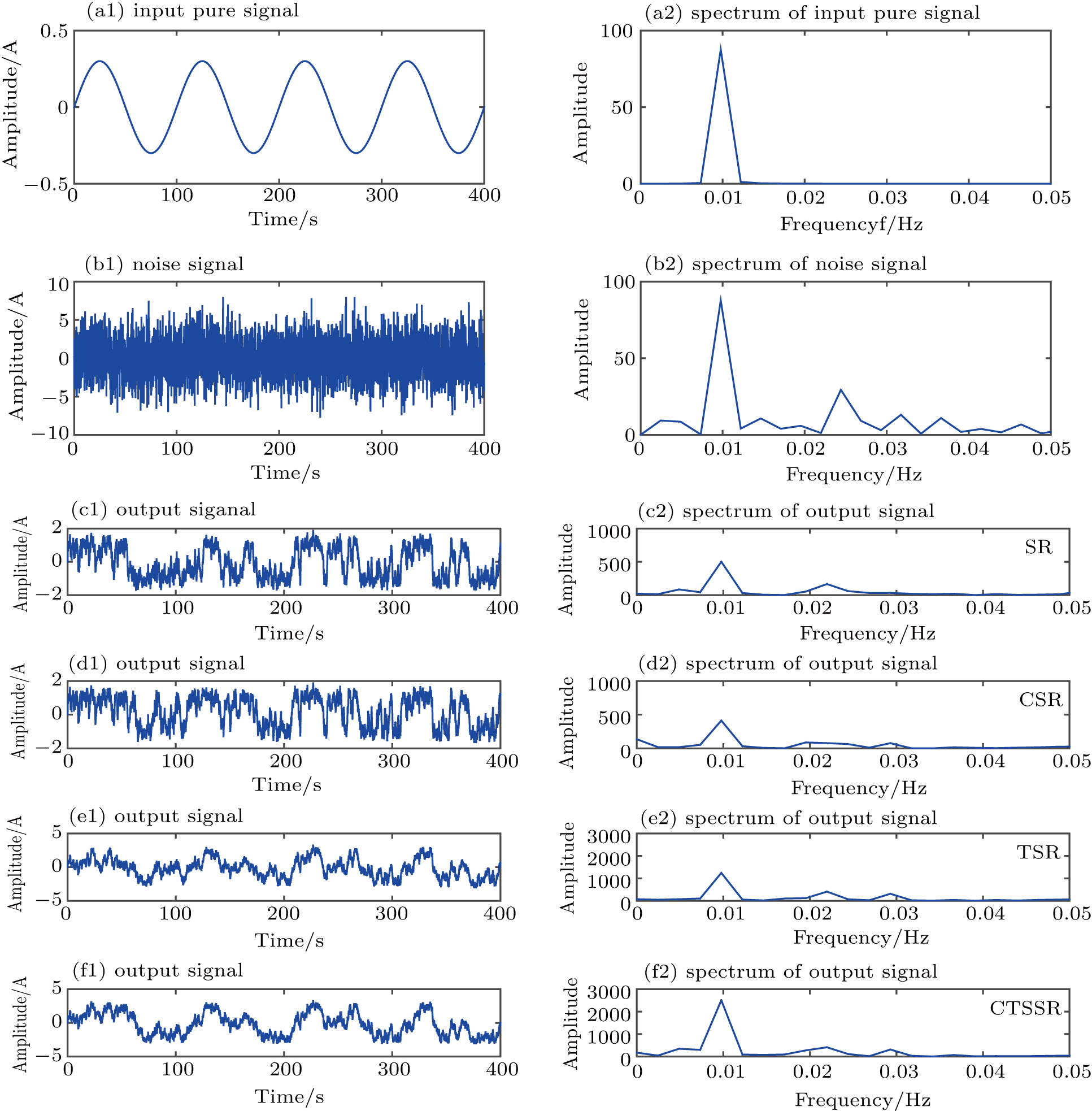
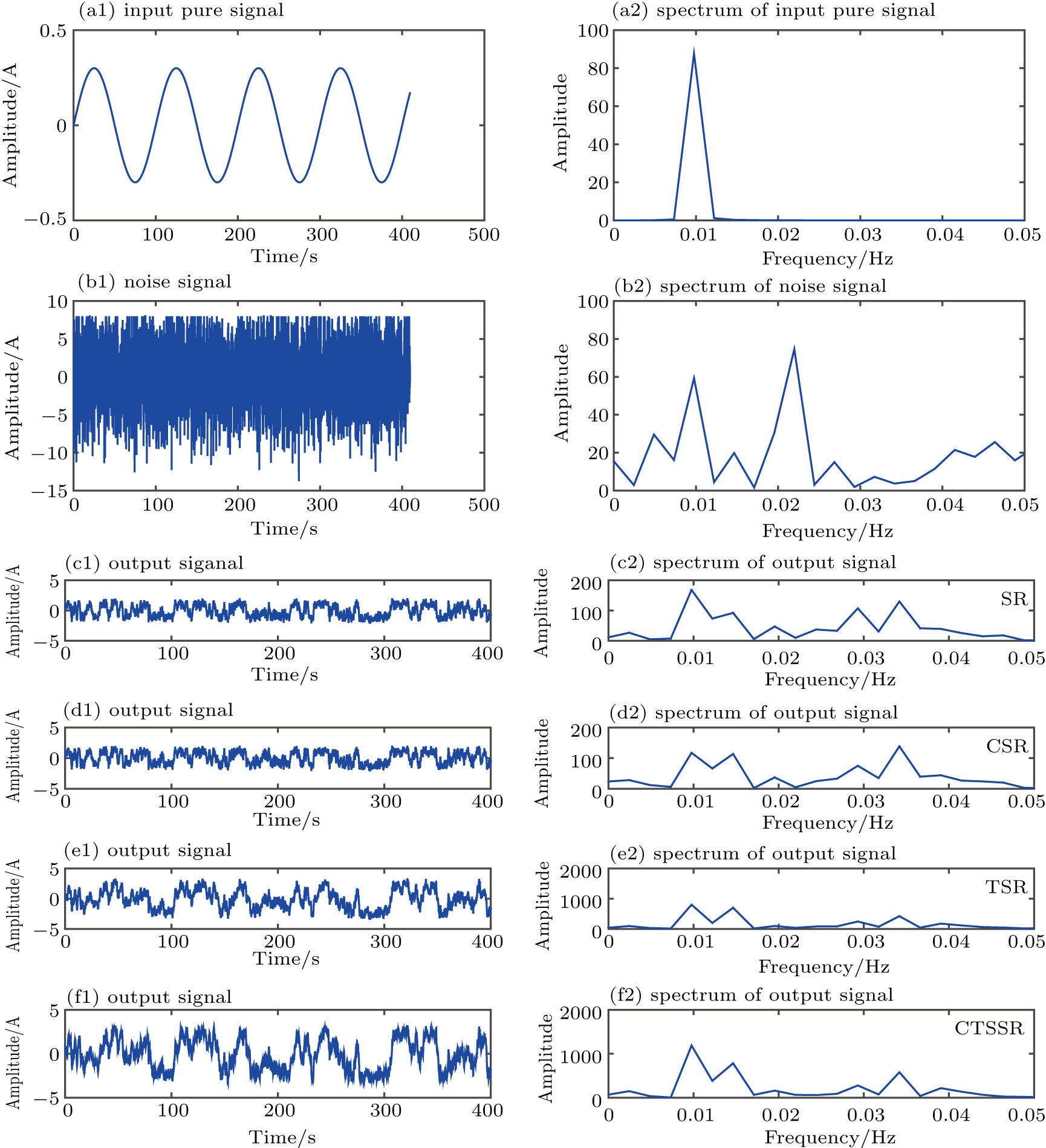
In the aspect of SNR, we are informed that the CTSSR is much better than the others. Furthermore, we implement a study in time domain and frequency domain to compare their performance. Based on the above conclusion that the CTSSR has better performance not only under relatively weak noise, but also under strong noise, to confirm this superiority, we choose different values of noise intensity D to conduct simulation experiments in both time domain and frequency domain. Firstly, we set noise intensity D = 3.0. Figures 10(a) and 10(b) show the original signal without white Gaussian noise and the noise signal with white Gaussian noise and their spectra. We can see that it is pretty hard to distinguish the original sinusoidal signal in Fig. 10(b). Figures 10(c)–10(f) show the output signals and their spectra processed by the SR, CSR, TSR, and CTSSR, respectively. We can intuitively draw the conclusion that the performance of SR and CSR is worse than that of CTSSR under the strong noise background, and the performance of TSR is nowhere near as excellent as that of CTSSR, although it is better than that of the two others. Thus, the superiority of CTSSR is explained by a flagrant contrast. In addition, we can prove that the merits of coupling and multi-stable state by contrasting these subfigures. That is to say, by contrasting Fig. 10(c) to Fig. 10(e), or by contrasting Fig. 10(d) with Fig. 10(f), we can be informed that the complexity of potential that is a symbol of complexity of system’s dynamics is equivalent to the performance of the system. Analogously, if we compare Fig. 10(c) with Fig. 10(d) or Fig. 10(e) with Fig. 10(f), we will be conscious that coupling could play a powerful role in improving the performance of the SR system. These two conclusions support the superiority of CTSSR naturally.

Fig. 10. (color online) (a) The original sinusoidal signal and its spectrum. (b) The noise signal and its spectrum. (c)–(f) The output signals with their spectra processed by SR, CSR, TSR, and CTSSR, respectively, when D is equal to 3.0.

By increasing the noise intensity D to 6.0, we obtain a new telltale figure, as shown in Fig. 11. At first, we can find out that the original signal has already been overwhelmed in the strong noise from Fig. 11(b). Obviously, it is impossible to distinguish the sinusoidal signal out from the SR and CSR systems (Figs. 11(c) and 11(d)). Moreover, if we analyze Figs. 11(e) and 11(f), we will find that the coordinate value is hardly the highest in the frequency spectrum of TSR when f = 0.01 Hz. Usually, it could result in an erroneous judgment. On the contrary, we can still determine the frequency of the sinusoidal signal from Fig. 11(f). So, the advantage of the CTSSR system is proved once again. Hereto, we have proved the merits of the system we put forward from two perspectives: time-frequency domain and SNR.

Fig. 11. (color online) (a) The original sinusoidal signal and its spectrum. (b) The noise signal and its spectrum. (c)–(f) The output signals with their spectra processed by SR, CSR, TSR, and CTSSR, respectively, when D is equal to 6.0.
4. Conclusion

In this paper, a novel SR model CTSSR is proposed. We study the effects of the system parameters on its characteristics firstly and then select a set of system parameters that are relatively optimal according to its performance in SNR. Finally, the comparisons between the CTSSR and other SR models in SNR and time-frequency domain are carried out. The results of numerical experiments on SNRgain show that the SNRgain of CTSSR is higher than that of other SR models including SR, CSR, and TSR under strong background noise. It is confirmed by numerical experiments in the time and frequency domain that the ability of our proposed system in detecting a weak signal is better than that of the others, especially when the noise intensity is high. In view of all its merits, it has been proved theoretically that the proposed model is beneficial to detect a weak signal overwhelmed in strong noise. We hope it has a broad prospect of application to engineering in the future.

Reference
[1] Benzi R Sutera A Vulpiani A 1981 J. Phys. A: Math. Gen. 14 L453
[2] Xiao W Gang H Chun Y Rong L De G Fu W 1994 Acta Phys. Sin. (oversea edition) 3 667
[3] Duan F Abbott D 2005 Phys. Lett. 344 401
[4] Yang Y B Tao W M Huang J M Xu B H 2012 Chin. Phys. 21 301
[5] Wang C J 2010 Chin. Phys. 19 112
[6] Liu J Wang Y G Zhuo Q Q Liu J 2016 Chin. Phys. 25 100501
[7] Jung P Hänggi P 1991 Phys. Rev. 44 8032
[8] Gammaitoni L Marchesoni F Santucci S 1995 Phys. Rev. Lett. 74 1052
[9] Lutz E 2001 Phys. Rev. 64 051106
[10] Gandhimath V M Rajasekar S Kurths J 2006 Phys. Lett. 360 279
[11] Mankin R Laas K Laas T Reiter E 2008 Phys. Rev. 78 031120
[12] Saikia S 2014 Physica 416 411
[13] Neiman A Schimansky-Geier L 1995 Phys. Lett. 197 379
[14] Lin M 2008 Acta Phys. Sin. 57 2048 in Chinese
[15] Lin M Fang L M Zhu R G 2008 Acta Phys. Sin. 57 2638 in Chinese
[16] Kenfack A Singh K P 2010 Phys. Rev. 82 046224
[17] Min L 2011 Acta Phys. Sin. 60 020501 in Chinese
[18] Yu H T 2012 Acta Phys. Sin. 61 068702 in Chinese
[19] Yang T Zhang H 2016 Int. J. Non-Linear Mech. 67 42
[20] Li J Chen X He Z 2013 Journal of Sound & Vibration 332 5999
[21] Han D Li P An S Shi P 2016 Mechanical Systems & Signal Processing s70 995
[22] Shi P Li P An S Han D 2016 Discrete Dynamics in Nature and Society 2016 1