† Corresponding author. E-mail:
The structural, electronic, and optical properties of Zn3(VO4)2 are investigated using full potential linearized augmented plane wave (FP-LAPW) method within the framework of density functional theory (DFT). Various approaches are adopted to treat the exchange and correlation potential energy such as generalized gradient approximation (GGA), GGA+U, and the Tran–Blaha modified Becke–Johnson (TB-mBJ) potential. The calculated band gap of 3.424 eV by TB-mBJ is found to be close to the experimental result (3.3 eV). The optical anisotropy is analyzed through optical constants, such as dielectric function and absorption coefficient along parallel and perpendicular crystal orientations. The absorption coefficient reveals high absorption (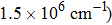
Metal vanadates normally denoted as M3(VO4)2 where M is a transition or alkaline earth metal, such as Mg3(VO4)2, Zn3(VO4)2, Co3(VO4)2, and Ni3(VO4)2, show interesting magnetic,[1] photocatalytic,[2] and light emission properties.[3,4] These compounds show orthorhombic crystal symmetry and lie in space group Cmca. Zn3(VO4)2 is one example of ternary oxide phosphor due to its large band gap of about 3.25 eV.[5,6] It has three polymorphs: α-, β-, and γ-phases. Among them, α-Zn3(VO4)2 is a stable phase at room temperature,[7] which has orthorhombic crystal structure with lattice parameters a = 6.088 Å, b = 11.489 Å, and c = 8.280 Å.[8]
Extensive experimental work has been conducted to investigate the structural and photonic properties of Zn3(VO4)2,[4,8–14] but rarely is theoretical work done to study this novel material. Electronic and magnetic properties of other metal vanadates such as Co3(VO4)2 and Ni3(VO4)2 have been studied theoretically in the last decade,[1,15–18] but very few reports related to the electronic band structure of Zn3(VO4)2 are found,[19–21] while the optical properties have not been reported until now to the best of our knowledge. The interesting photonic and photocatalytic properties of Zn3(VO4)2 motivate us to study the electronic and optical properties of Zn3(VO4)2 in detail.
In density functional theory (DFT), different basis functions, such as augmented plane wave (APW), projector augmented wave (PAW),[22,23] and full potential linearized augmented plane wave (FP-LAPW),[24,25] are chosen to solve the Kohn–Sham equation. The ab-initio calculations of the electronic structures of Zn3(VO4)2 and Mg3(VO4)2 have been performed using the PAW method under different exchange correlation potential functionals (GGA, GGA+U, TB-mBJ).[19] It was noted that the band gap of these materials depends strongly on the exchange correlation potential energy used for calculations. In the present study, the full potential linearized augmented plane wave (FP-LAPW) method with the same exchange correlation functionals is adopted to investigate the structural and electronic properties of Zn3(VO4)2, and a comparison is made between PAW and LAPW methods. Moreover, the optical and photoluminescence properties of Zn3(VO4)2 are also investigated.
Calculations are carried out using GGA, GGA+U, and TB-mBJ approximations as the exchange correlation potential energy implemented in the Wien2k package.[26] In this study, Hubbard potentials U for Zn and V are taken as 4.7 eV and 3.25 eV, respectively. Normally, it is observed that the GGA approximation underestimates the band gap compared to the experimental band gap, which is its main disadvantage. To resolve this shortcoming, other methods such as GGA+U and TB-mBJ approximations are used. These approximations work well for the systems containing strongly correlated 3d, 4f, or 5f electron orbitals. Compared to GGA or GGA+U, the TB-mBJ approximation gives the band gap energy in close agreement with the experimental data.
For the crystal potential, the muffin-tin model is adopted in which the unit cell is divided into two regions: core and valence. The electron density lying inside the muffin-tin radius (RMT) is treated as the core whereas outside is the valence. In the core states, the electronic wave functions are considered as atomic-like wave functions (spherical harmonics type), while in the valence states, the wave function is taken in the form of plane waves plus local orbitals (LO), therefore named as full potential LAPW. In comparison to the LAPW method, the PAW method assumes a pseudo potential in the core states and plane waves in the valence states. In the present study, the non-overlapping sphere of radius RMT around each atom is chosen in a way that no charge leaks out from the core and the total energy convergence is ensured to the desired energy, ∼0.0001 eV between the energy steps. The RMT for Zn, V, and O atoms are taken as 1.62 a.u., 1.58 a.u., and 1.2 a.u., respectively. A mesh of 19×19×12 k points for electronic and optical calculations is made with 
Before the calculations for the electronic structure and optical properties, we have optimized the Wyckoff positions of all atoms in the unit cell with a convergence criterion of 0.05 mRyd/Å. The optimized positions along with experimental[8] and reported theoretical[19] Wyckoff positions of different atoms are presented in Table
| Table 1.
Optimized positions of atoms in a unit cell. . |
Figure
The bandgap of Zn3(VO4)2 is calculated by using GGA, GGA+U, and TB-mBJ exchange correlation functionals as shown in Fig.
 | Fig. 2. (color online) Calculated band structures of Zn3(VO4)2 by using (a) GGA, (b) GGA+U, and (c) TB-mBJ approximations. |
| Table 2.
Calculated band gap and static dielectric function in x and z directions using GGA, GGA+U, and TB-mBJ approaches. . |
The electronic distribution is well described by the total density of states of Zn3(VO4)2 and the partial density of Zn, V, and O using GGA, GGA+U, and TB-mBJ exchange potentials (Fig.
 | Fig. 3. (color online) Calculated (a) total and (b) partial density of states for Zn3(VO4)2 using GGA, GGA+U, and TB-mBJ approximations. |
Fig.
The optical properties of Zn3(VO4)2, i.e., dielectric function and absorption, are described in x and z crystal orientations with respect to the photon polarization direction. Being a property of the anisotropic crystal, the dielectric function shows slightly different behaviors in the prescribed directions (table
As ε2(ω) is strongly connected to the electronic transitions, it can be investigated with the help of the electronic partial density of states as illustrated in Fig.
Real and imaginary dielectric functions of Zn3(VO4)2 in two crystallographic directions x and z are studied by using GGA, GGA+U, and TB-mBJ approaches (Fig.
 | Fig. 5. (color online) (a) Real part and (b) imaginary part of the dielectric function, and (c) absorption coefficient versus energy using GGA, GGA+U, and TB-mBJ approximations. |
The static dielectric function ε1(0) is an important parameter which is calculated at the zero frequency limit. It has a strong relationship with the bandgap energy as described by the Penn model[28]
The absorption coefficient α (ω) can be calculated directly with dielectric function ε (ω) by using the following relation:[28]
The threshold energy of absorption for Zn3(VO4)2 is calculated by using all mentioned approximations, which lies in the range 2.3–2.9 eV in x and z crystal orientations, respectively (Fig.
The structural, electronic, and optical properties of Zn3(VO4)2 are calculated by using FP-LAPW method. GGA, GGA+U, and TB-mBJ approaches are used for the exchange correlation potential energy. The indirect bandgaps calculated by using these methods are 2.703 eV, 3.094 eV, and 3.424 eV, respectively. Among these methods, TB-mBJ gives the best results that match the theoretical and experimental studies. It is found that the V-3d states have a major contribution to the conduction band whereas hybridized Zn-3d and O-2p states participate in the valence band. The static dielectric function calculated by using these approximations is 5.179, 4.764, and 3.744, respectively. The absorption coefficient is very high (∼106 cm−1) in the ultraviolet region, which implies that this material is suitable for exciting high-energy photons and can be utilized for photoluminescence and photo catalysis applications. Moreover, an optical anisotropy is observed for different crystal orientations.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |





