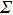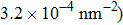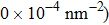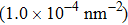Cite this Article
Fang Gang, Sheng Nan, Jin Tan, Xu Yousheng, Sun Hai, Yao Jun, Zhuang Wei, Fang Haiping. Hydrophobic nanochannel self-assembled by amphipathic Janus particles confined in aqueous nano-space. Chinese Physics B, 2018, 27(3): 030505  
Permissions
Hydrophobic nanochannel self-assembled by amphipathic Janus particles confined in aqueous nano-space
Fang Gang1, 2, 3, Sheng Nan1, Jin Tan2, Xu Yousheng4, Sun Hai5, Yao Jun5, †, Zhuang Wei2, ‡, Fang Haiping1, §
Division of Interfacial Water and Key Laboratory of Interfacial Physics and Technology, Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Shanghai 201800, China
State Key Laboratory of Structural Chemistry, Fujian Institute of Research on Structure of Matters, Chinese Academy of Sciences, Fuzhou 350002, China
University of Chinese Academy of Sciences, Beijing 100049, China
School of Light Industry, Zhejiang University of Science and Technology, Hangzhou 310023, China
School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266555, China

 

† Corresponding author. E-mail: yaojun@upc.edu.cn wzhuang@fjirsm.ac.cn fanghaiping@sinap.ac.cn

Abstract

Hydrophobic nanochannel plays a significant role in many physical, biological, and geological phenomena and exhibits impressive applications due to both its ubiquitous distribution and great ability to transport hydrophobic molecules, including various oils and gases. Based on theoretical modeling, we herein reveal that the amphipathic Janus nanoparticles have a large probability to self-assemble into uninterrupted hydrophobic nanochannels inside the aqueous nano-space, although there are large portions of the Janus nanoparticles to be hydrophilic. The key to this observation is the attractions between the hydrophobic regimes on neighboring amphipathic Janus particles through hydrophobic interaction in aqueous nano-space. More surprisingly, the permeation efficiency of hydrophobic molecules through the uninterrupted hydrophobic channel in Janus particles aggregate is even higher than that in the aggregate of hydrophobic particles. We note that the proposed amphipathic Janus particles can be transported to the appropriate positions by the water since the hydrophilic regimes still remain a strong particle–water interaction. We also note that most natural subsurface rocks are not completely hydrophobic or hydrophilic but have complex surfaces with inhomogeneous wetting property. Our work therefore provides a detailed molecular level understanding of the formation of underground strata as well as the new insight for constructing the artificial hydrophobic channels for various applications, such as the design of proppants to enhance the recovery of the unconventional oil/gas.

PACS: 05.65.+b;05.60.-k;83.10.Rs
Keyword:amphipathic Janus particle;self-assembly;uninterrupted hydrophobic channel;water blockage
1. Introduction

Hydrophobic nanochannel, which provides an efficient way to transport hydrophobic molecules, plays an essential key role in a plethora of important physical processes ranging from the energy fuel storage,[1,2] nanofluidic channel,[3–5] hydrophobicity-based gating and separation,[6–8] to oil and shale gas exploitation.[9] One of the most direct mechanisms of the hydrophobic channel formation is through the self-assembly[10–13] of hydrophobic nanoparticles in aqueous solutions. However, a solid particle in nature rarely possesses a completely hydrophobic surface. Instead, most of them have a mixed surface with both hydrophobic and hydrophilic regimes.[14] Moreover, in the practical application, due to the weak interaction with water, it is very difficult to insert the hydrophobic nanoparticles into a confined nano-space. For example, in the hydraulic fracturing for the exploitation of oil and shale gas, proppants are widely used to prop the fractures and help the escape of oil/gas under the huge pressure underground. The hydrophilic particles are usually used as proppants since they can be easily inserted into the fractures by the water flow owing to their strong water–particle interaction. It is clear that a hydrophobic channel cannot be formed by those hydrophilic particles. In fact, a big and well-known problem encountered while using these hydrophilic proppants is that, together with water, they usually block the permeation of the hydrophobic oil/gas (which is called water blocking[15]) and thus greatly reduce the oil/gas recovery.[16,17] We note that there are many hydrophobic channels, such as carbon nanotubes,[18] fabricated and studied in the past several decades.[19–26] However, these artificial hydrophobic nanochannels still remain unavailable for many practical applications.

A nanoparticle with an inhomogeneous surface wetting property (so called amphipathic Janus particle[27–29]) may provide a new way to address the challenge. Amphipathic Janus particles have exhibited impressive potential in a wide range of applications, such as controllable pore,[30,31] emulsion polymerization,[32] water-repellent fibers,[33] and colloid surfactant.[34] The aggregating behavior of amphipathic Janus particles in an interface has been studied both theoretically and experimentally.[35–38] In the confined space, very recently, Fernandez et al.[39] theoretically studied the assembly process of the two-dimensional model Janus disks in a confined channel-like environment and received an energetically stable morphology. Little attention, however, has been paid to the formation of the hydrophobic nanochannel aggregated by the amphipathic Janus particles in aqueous nano-space, especially on the behavior of the permeation of hydrophobic molecules through the hydrophobic nanochannel.

We herein show, based on the theoretical modeling, that amphipathic Janus particles have a large probability to self-assemble into an uninterrupted hydrophobic nanochannel in the confined aqueous nano-space. Although the amphipathic Janus particles possess some hydrophilic regimes on the surface, the hydrophobic regimes on neighboring amphipathic Janus particles attract each other through hydrophobic interaction, and therein the uninterrupted hydrophobic channel spontaneously emerges. More surprisingly, the permeation efficiency of hydrophobic molecules through the uninterrupted hydrophobic channel of aggregated Janus particles is even higher than the permeation efficiency through the hydrophobic channel of aggregated hydrophobic particles. The hydrophilic regimes on the Janus particles still have a strong interaction with water so that the particles can be inserted into the nano-space by the water flow. We therefore provide a detailed molecular level understanding of the formation of underground strata due to the amphipathic property of most natural subsurface rock. Furthermore, our work suggests a possible new treatment to construct artificial hydrophobic channels for various applications, including the design of proppants to enhance the recovery of unconventional oil/gas.

2. Method

Two sets of MD simulations are performed and the details of the simulations are displayed as follows to figure out the self-assembly process of the nanoparticles in confined aqueous nano-space as well as their performance in enhancing hydrophobic molecule flux through a water layer.

The first set of self-assembly simulation systems are performed in the NVT ensemble using Gromacs 4.5.4.[40] GMX forcefield is applied.[41] The common SPC/E water model[42] is used as well. A constant temperature is maintained by the velocity-rescale method with the coupling time of 1 ps. The temperature of the simulation is set to be 300 K. The simulation time is 100 ns with the timestep of 2 fs. The simulation data is collected with the frequency of per 1000 steps. The whole simulation box is set to be 5.200 × 6.000 × 23.191 nm3 accordingly. The periodic boundary condition is applied to all three directions. The long-range electrostatic interaction is calculated by the particle-mesh Ewald (PME) method with a real space cutoff of 1.2 nm. The cutoff distance of the van der Waals (vdW) interaction is 1.2 nm as well. The Lennard–Jones parameters of the carbon atom on methyl (-CH3) and the oxygen on hydroxyl (-OH) are εcc= 0.180 kcal/mol, σcc= 3.786 Å and εoo= 0.203 kcal/mol, σoo= 2.955 Å. The initial velocity is generated according to the Maxwell distribution at the temperature of 300 K. Using the untied atom model, the methyl (-CH3) in our systems is represented by the single C atom according to the parameters in the forcefield.

Many parameters in the second set of simulations keep the same as the first one. However, the whole simulation box is set to be 5.200 × 6.000 × 40.000 nm3, namely, there is enough empty space on the right for gas to diffuse. The methane here is also denoted by the single sphere with the parameters of εcc= 0.302 kcal/mol and σcc= 3.710 Å. The main simulation time is set to be 200 ns with the timestep of 2 fs after the optimization process for 100 ps.

The Molcal package[43] is used to draw the hydrophobic nanochannel among the particle configurations according to the vdW interaction distance of the atoms consisting the nanochannel. The detailed description of this method has been presented (Fig. S3).

3. Results and discussion
3.1. Self-assembled configurations of the nanoparticles

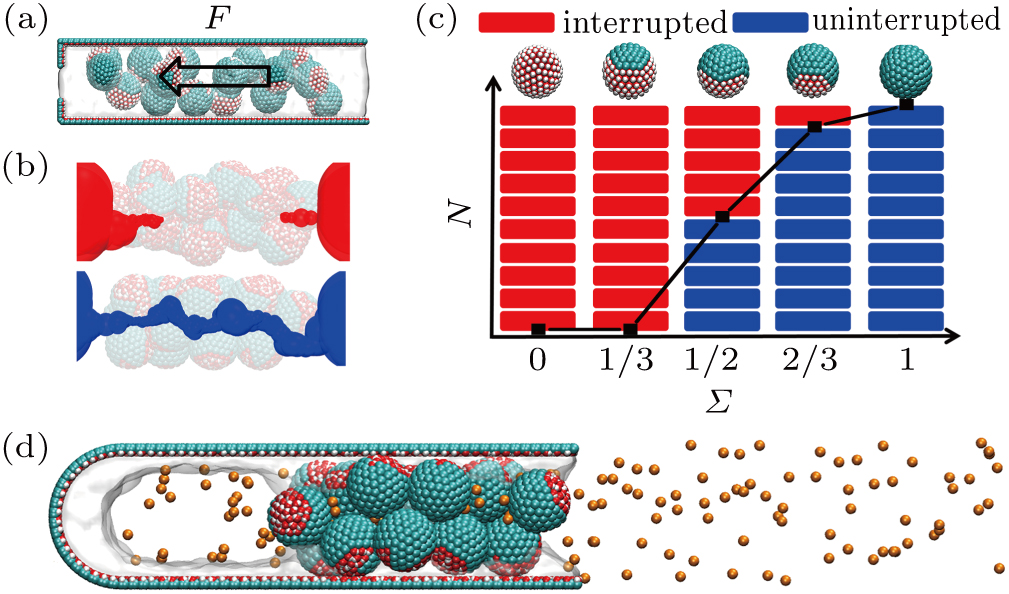
Three types of the model amphipathic Janus particles, with the hydrophobic area of nearly 2/3 (pattern-1), 1/2 (pattern-2), and 1/3 (pattern-3) on the surface, are used in our study. The surfaces of the particle are modified using methyl (-CH3) and hydroxyl (-OH) to adjust the local hydrophobicity. Considering the affinity of hydrophilic groups to each other during the preparation,[44] we design the patterns with localized amphipathic regimes on the particle surface (Fig. S1). For comparison, we also prepare the hydrophilic and hydrophobic particles where the surface is completely hydrophilic or hydrophobic.

We first study the aggregated configurations of those particles in a nano-size space,[45] which determine the methane permeability since the capillary effect is significant in the micro-pores and water can completely block the hydrophilic fractures. The simulation system is composed of 16 particles soaked in water (Fig. 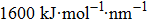1(a)). The particles and water are confined by a model fracture of 5.7 nm vertical separation distance (details of fracture construction and particle positioning are given in Fig. S2). Initially, the particles are placed randomly but do not overlap with each other or with the inner surface of the nano-space. For each type of particle, 10 sets of initial configurations with different particle positions and orientations are used (to the best of our capability) to generate a statistically reasonable result. To consider the influence of water flow during the hydraulic fracturing, a constant force with the magnitude of toward the left side is applied to the particle group in our simulation. The force is equally distributed to the particles, driving them to the left side of our system. 100 ns MD simulations are performed.

Fig. 1. (color online) Proportion of forming an uninterrupted hydrophobic nanochannel inside the self-assembly particle configurations and its application in enhancing the gas permeation. (a) Initial configuration of the first set of simulations. The system is composed of fracture and 16 particles socked in the water (OH groups: red and white, carbon atoms and CH3 groups: green). The water is represented by the transparent part. A small force towards the left side has been applied to the particles. (b) Example of forming interrupted and uninterrupted hydrophobic nanochannels inside the particle assemblies. The red and blue segments stand for the interrupted and uninterrupted nanochannels, respectively. (c) Number of the systems forming interrupted and uninterrupted hydrophobic nanochannels inside the aggregated particle configurations for each kind of particle in all 10 sets of systems. Red and blue blocks denote the number of the system forming interrupted and uninterrupted nanochannels, respectively. represents the proportion of the hydrophobic regime on each particle surface. N denotes the number of the systems with uninterrupted hydrophobic nanochannels (together with the black line). (d) Main scheme of the simulation system to test the permeability of the methane through the blockage caused by the particle configuration together with the water. Typical result of 200 ns is shown for the pattern-1 system. The orange spheres represent the methane molecules.

For the patterned as well as the fully hydrophobic systems, the hydrophobic regimes of the particles are likely to associate together and generate the tortuous and water-repelling nano-crevice (namely, hydrophobic nanochannel). The typical configurations of the interrupted and uninterrupted hydrophobic nanochannels inside the particle assemblies are presented in Fig. 1(b). In Fig. 1(c), for pattern-1 (pattern-2) particles, 9(5) out of 10 sets of simulation trajectories have the uninterrupted hydrophobic nanochannels connecting two ends of the assemblies (see also Fig. S3). No uninterrupted hydrophobic nanochannel exists inside the assemblies of pattern-3 systems. As a comparison, the assemblies of pure hydrophobic particles always have the uninterrupted nanochannels while those of pure hydrophilic particles have no hydrophobic nanochannel. We also note that it is quite a bit harder for the fully hydrophobic particles flowing with the fluid into the fractures (Fig. S4). The properly engineered Janus particles are therefore the optimized candidate for extracting methane confined in the fracture. In the following, we carry out a detailed analysis for the methane permeability in the micro-pore jammed by water and the aforementioned proppant particles.

3.2. Permeability of methane

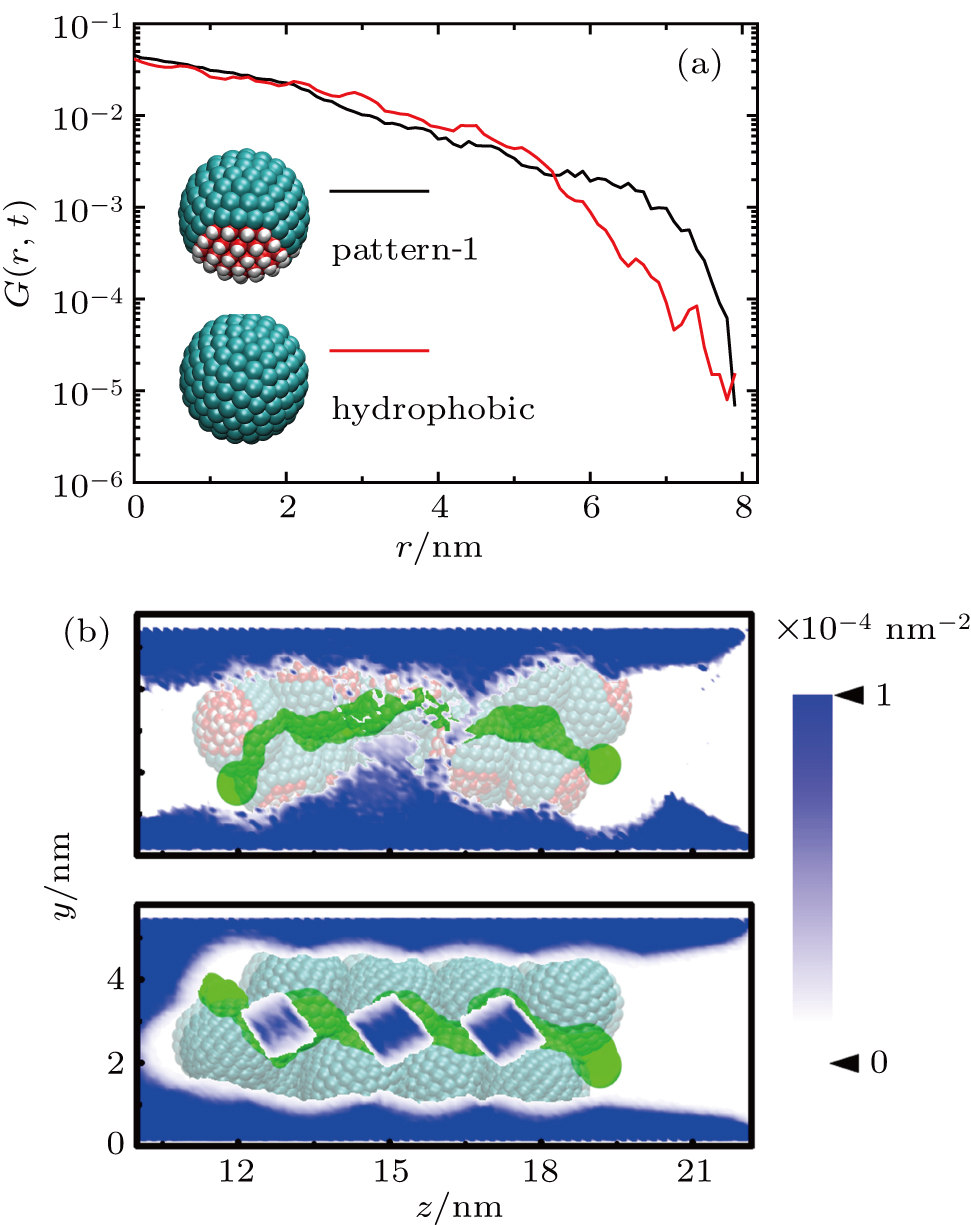
We now study the molecular details of methane permeation through these hydrophobic nanochannels. The aggregated particle configurations obtained from previous simulations are inserted into a tube-like fracture opened at one end. The space between the hydrophilic inner wall of nano-space and the particle assembly is filled with methane molecules, which are separated from the particle assembly by a cubical water body (Fig. S5). The geometry of a typical pattern-1 system at 200 ns is shown in Fig. 1(d). The average numbers of the methane molecules escaping from the blocking region with respect to time are presented in Fig. 2. Intuitively, the completely hydrophobic assembly is much more permeable compared to the completely hydrophilic assembly. The striking observation here, however, is that some of the partially hydrophilic assemblies such as pattern-1 and pattern-2 can be more permeable than the completely hydrophobic one despite the weaker connectivity of their hydrophobic nanochannels. As shown in Fig. 2, pattern-1 and pattern-2 systems have the fast escaping rate. For the pattern-1 system, the average escaping number of the methane is 82.6 in 200 ns, similar to pattern-2 systems of 90.3. As a comparison, the average escaping number in the hydrophobic system is only about 69.9 in 200 ns, much lower than the other two systems. The detailed escaping number of each system and the average result of all systems have also provided (Fig. S6).

Fig. 2. (color online) Escaping numbers of the methane in different particle configurations. Number of the methane gas permeating out of the blockage versus the simulation time in the typical pattern-1, pattern-2, and hydrophobic systems. t and n are the simulation time and the number of the escaping methane molecules, respectively. The blue, purple, and orange colors correspond to the results of pattern-1, pattern-2, and hydrophobic systems. Symbol and line are used to represent one typical result and the averaged result of these three systems, respectively.
3.3. Configuration of the water body

To explain the unexpected observations of permeability, we next examine the configuration of the water body in the tube.[46] Within ∼20 ns the initial cubical water bodies in all the systems gradually collapse and reach the converged shapes. This stable stage then lasts till the end of the simulations (see the Appending Movies).

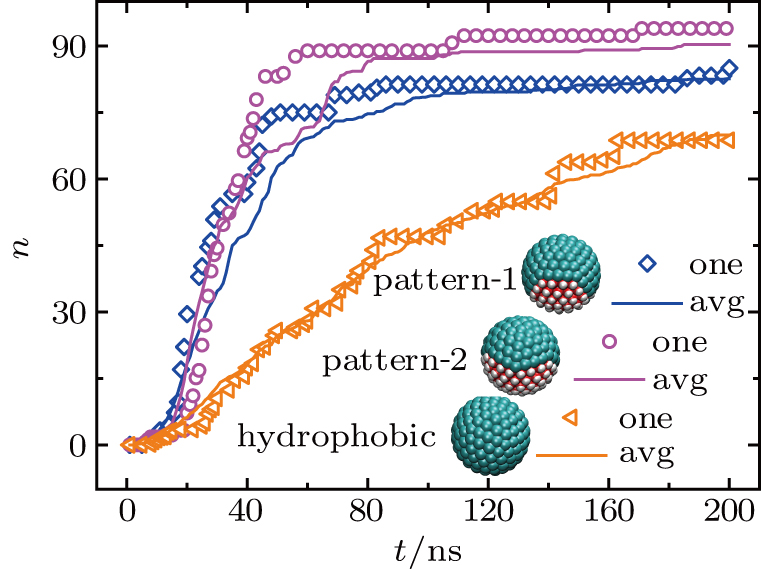
For the typical system with the pattern-1 particles, the water blockage between the methane molecules and the nanoparticle assembly is broken after 20 ns (Fig. 2), which leads to the fast methane molecules escaping (∼85.0 in 200 ns). The number of the escaped methane molecules increases quickly from t = 20 ns to t = 50 ns, and becomes constant afterward. Similar results are observed for pattern-2 system. In these two systems, sizable hydrophilic regions are formed in the fracture within the particle assemblies. Water molecules are absorbed into these hydrophilic regions as well as onto the inner surface of the fracture, resulting in the shrinking or destruction of the initial water blockage.

In the complete hydrophobic system, on the other hand, no hydrophilic region exists. Water molecules are only absorbed onto the fracture surface. The water blockage remains intact during the whole simulation. A methane concentration gradient exists in the water body, which drives the permeation of methane gas across the water blockage.[47] After all, methane can still permeate through the complete hydrophobic system, but the permeation is much slower comparing to the patterned systems with uninterrupted hydrophobic nanochannels.

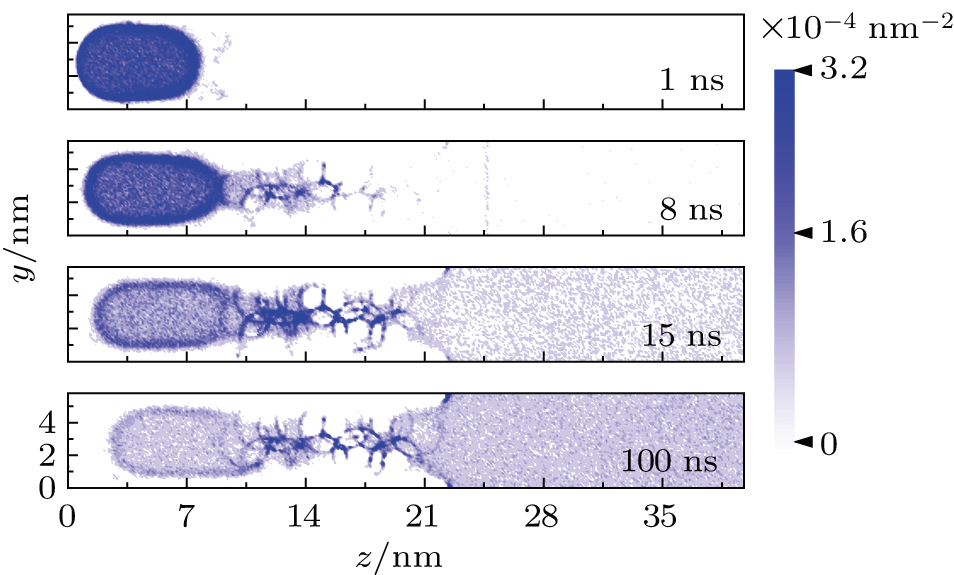
3.4. Time evolution of methane density distribution

To study the methane diffusion in the confined fracture, we calculate the time dependent spatial density distribution of the methane at four different moments 1 ns, 8 ns, 15 ns, and 100 ns. The normalized density (average over 1 ns) of the methane gas is projected to the yz plane. The density plot for the pattern-1 system is presented in Fig. 3. Plots for other systems are also provided (Fig. S7).

Fig. 3. (color online) Diffusion process of the methane in the typical pattern-1 system. Density distributions of the methane gas in the pattern-1 system versus the simulation time. The figure shows the average distributions of the methane gas per ns at the simulation time around 1, 8, 15, and 100 ns. Different color gradients stand for the different densities of the methane gas. The blue color represents the highest density ( of the methane gas around and the white regions stands for the lowest density ( .

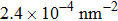
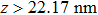
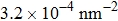
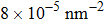
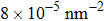
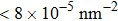
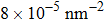
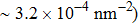
At 1 ns, the density of the methane gas in the blocking region from 0 to 8 nm in the z direction is higher than and no methane molecule exists in the free diffusion region (out of the fracture) where . The methane gas has a higher density, nearly , at the region near the fracture surface due to the attraction. At 8 ns, the density inside the blocking region decreases, while that in the particle region increases to a magnitude of more than . No methane exists in the diffusion region so far. At 15 ns, the methane density inside the blocking/particle region continues to decrease/increase compared to 8 ns. The density in the free diffusion region increases to less than . At 100 ns, the density in the blocking region and the free diffusion region reaches a dynamic equilibrium. The balanced density of the methane gas in both blocking and diffusion regions is . The methane density is up to near the fracture surface, and becomes extra high ( inside the hydrophobic nanochannel in the particle assembly.

3.5. Confined methane diffusion within the hydrophobic nanochannels

Discussions in the previous sections established that with the same amount of water, certain assemblies formed by amphipathic Janus particles can absorb water into their hydrophilic nano-crevices, which leads to the thinner water blockage and therefore faster methane permeation. In the section, we demonstrate that even after methane molecules pass through the water blockage and reach the hydrophobic nanochannels in the particle assemblies, their permeation is still faster for some of the patterned systems with an uninterrupted nanochannel than the completely hydrophobic one.

The self-diffusion behavior of methane within the particle assemblies is described using van Hove distribution G(r, t).[48,49] This function is defined as the average probability to find a particle at the position r at the time t, given that the particle is located at the origin point at t = 0. G(r, t) of the methane inside the hydrophobic nanochannels along the diffusion direction are calculated for the typical pattern-1 and hydrophobic systems at the time interval of 2 ns (Fig. 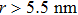4(a)) (see also Fig. S8). For the diffusion distance , G(r, t) of the pattern-1 system is always larger than that of the hydrophobic one, which means that methane molecules diffuse faster in the pattern-1 system compared to the completely hydrophobic system. This is due to the existence of some residual water inside the completely hydrophobic assemblies (Fig. 4(b)),[50] which forms the clusters and retards the methane diffusion (Fig. S9, Fig. S10, and the Appending Movies).

Fig. 4. (color online) Self-diffusion difference of the methane in the hydrophobic nanochannel between pattern-1 and hydrophobic systems. (a) Self-diffusion behavior of methane gas inside the particle configurations for hydrophobic and pattern-1 systems by using van Hove distribution G(r, t). The difference between pattern-1 and hydrophobic systems in the diffusion direction are shown within 2 ns. The black and red lines correspond to the result of pattern-1 and hydrophobic systems, respectively. (b) Density distributions of water around the particle configurations in pattern-1 and hydrophobic systems. Blue and white colors represent the highest and lowest density , respectively. The particle assemblies and the uninterrupted hydrophobic nanochannels shown as the green segments are also represented.

We note that the amphipathic Janus particle is easy to be carried with the fracturing fluid because of the sufficient friction between the particle and water. The moving ability of the particles with the water has a positive relationship with the hydrophilic proportions on each particle surface (Fig. S4).

4. Conclusion

Based on the theoretical modelling, we show that amphipathic Janus particles have a large probability to self-assemble into an uninterrupted hydrophobic nanochannel inside aqueous nano-space, and the probability has the positive relation with the hydrophobic proportion on each particle surface. Although the amphipathic Janus particles possess some hydrophilic regimes on the surface, the hydrophobic regimes on neighboring amphipathic Janus particles attract each other through hydrophobic interaction, and therein the uninterrupted hydrophobic channel spontaneously emerges. Surprisingly, the permeation efficiency of hydrophobic molecules through the uninterrupted hydrophobic channel of aggregated Janus particles is even higher than the permeation efficiency through the hydrophobic channel of aggregated hydrophobic particles. This is because the aggregated hydrophobic particles only repel and can hardly break the residual water layer in the nano-space, while the Janus particles can tear the residual water layer by adsorbing them on the hydrophilic parts. We note that the hydrophilic regimes on the Janus particles still have a strong interaction with water flow so that the particles can be transported to the appropriate positions by the water. Our work provides a detailed molecule level understanding in the formation of underground strata due to the amphipathic property of most natural subsurface rock, as well as providing new thinking and practical guidance to construct artificial hydrophobic channels for various applications, including the design of proppants to enhance the recovery of unconventional oil/gas.

Supplementary material

Detailed structures of five types of model particles, the geometry of the self-assembly simulation system, detailed information of using the Molcal package to draw the hydrophobic pathway in the particle configurations and the results, ability of different particles moving with the water fluid, geometry of methane permeating the simulation system, escaping numbers of the methane in all these 10 sets of simulations with different types of particles and the average results of them, distribution of the methane with the simulation time in pattern-2, pattern-3, hydrophilic, and hydrophobic systems, the van Hove distribution of the methane inside the hydrophobic assemblies in the pattern-1 and hydrophobic systems, comparison of van Hove distributions of the methane inside the hydrophobic pathway with and without water cluster, reason for the water trapped inside the particle assemblies in the hydrophobic system, and self-assemblies of the simple mixture of completely hydrophilic and hydrophobic particles are contained in the Supplementary material.

Supplementary movies are also provided.

Reference
[1] Liu C Fan Y Y Liu M Cong H T Cheng H M Dresselhaus M S 1999 Science 286 1127
[2] Comotti A Bracco S Distefano G Sozzani P 2009 Chem. Commun. 0 284
[3] Xie Q Xin F Park H G Duan C H 2016 Nanoscale 8 19527
[4] He J X Lu H J Liu Y Wu F M Nie X C Zhou X Y Chen Y Y 2012 Chin. Phys. 21 054703
[5] Gong X J Fang H P 2008 Chin. Phys. 17 2739
[6] Jiang C J Lesbani A Kawamoto R Uchida S Mizuno N 2006 J. Am. Chem. Soc. 128 14240
[7] Smirnov S N Vlassiouk I V Lavrik N V 2011 ACS Nano 5 7453
[8] Trick J L Wallace E J Bayley H Sansom M S P 2014 ACS Nano 8 11268
[9] Wang S Javadpour F Feng Q H 2016 Fuel 181 741
[10] Chandler D 2005 Nature 437 640
[11] Sánchez-Iglesias A Grzelczak M Altantzis T Goris B Perez-Juste J Bals S Van T G Donaldson J S H Chmelka B F Israelachvili J N 2012 ACS Nano 6 11059
[12] Guo P Tu Y S Yang J R Wang C L Sheng N Fang H P 2015 Phys. Rev. Lett. 115 186101
[13] Deng L Zhao Y R Zhou P Xu H Wang Y T 2016 Chin. Phys. 25 128704
[14] Wan R Z Wang C L Lei X L Zhou G Q Fang H P 2015 Phys. Rev. Lett. 115 195901
[15] Hanasaki I Nakatani A 2006 J. Chem. Phys. 124 144708
[16] Xu C Y Kang Y L You Z J Chen M J 2016 J. Nat. Gas Sci. Eng. 36 1208
[17] Shen Y H Ge H K Li C X Yang X Y Ren K Yang Z H Su S 2016 J. Nat. Gas Sci. Eng. 35 1121
[18] Iijima S 1991 Nature 354 56
[19] Hong E H Lee K H Oh S H Park C G 2003 Adv. Funct. Mater. 13 961
[20] Zhang Z Y Liang X L Wang S Yao K Hu Y F Zhu Y Z Chen Q Zhou W W Li Y Yao Y G 2007 Nano. Lett. 7 3603
[21] Ren Z F Huang Z P Xu J W Wang J H Bush P Siegal M P Provencio P N 1998 Science 282 1105
[22] Liu J Shi G S Guo P Yang J R Fang H P 2015 Phys. Rev. Lett. 115 164502
[23] Zhou Y H Guo W Jiang L 2014 Sci. China-Phys. Mech. Astron. 57 836
[24] Zhang Q L Jiang W Z Liu J Miao R D Sheng N 2013 Phys. Rev. Lett. 110 254501
[25] Lu H J Nie X C Wu F M Zhou X Y Kou J L Xu Y S Liu Y 2012 J. Chem. Phys. 136 174511
[26] Lu S Yao Z H Hao P F Fu C S 2010 Sci. China-Phys. Mech. Astron. 53 1298
[27] Walther A Müller A H E 2013 Chem. Rev. 113 5194
[28] Hu J Zhou S X Sun Y Y Fang X S Wu L M 2012 Chem. Soc. Rev. 41 4356
[29] Shah A A Schultz B Kohlstedt K L Glotzer S C Solomon M J 2013 Langmuir 29 4688
[30] Alexeev A Uspal W E Balazs A C 2008 ACS Nano 2 1117
[31] McConnell M D Kraeutler M J Yang S Composto R J 2010 Nano Lett. 10 603
[32] Walther A Hoffmann M Müller A H E 2008 Angew. Chem. Int. Ed. 47 711
[33] Synytska A Khanum R Ionov L Cherif C Bellmann C 2011 ACS Appl. Mater. Inter. 3 1216
[34] Tu F Q Lee D 2014 J. Am. Chem. Soc. 136 9999
[35] Binks B P Fletcher P D I 2001 Langmuir 17 4708
[36] Glaser N Adams D J Böker A Krausch G 2006 Langmuir 22 5227
[37] Park B J Brugarolas T Lee D 2011 Soft Matter 7 6413
[38] Chen X M Dong W Zhang X R 2010 Sci. China-Chem. 53 1853
[39] Fernández M S Misko V R Peeters F M 2014 Phys. Rev. 89 022306
[40] Hess B Kutzner C van der S D Lindahl E 2008 J. Chem. Theory Comput. 4 435
[41] Cornell W D Cieplak P Bayly C I Gould I R Merz K M Ferguson D M Spellmeyer D C Fox T Caldwell J W Kollman P A 1995 J. Am. Chem. Soc. 117 5179
[42] Berendsen H J C Grigera J R Straatsma T P 1987 J. Phys. Chem. 91 6269
[43] Bai Q F Perez-Sanchez H Zhang Y Shao Y H Shi D F Liu H X Yao X J 2014 Phys. Chem. Chem. Phys. 16 15874
[44] Yang J R Shi G S Tu Y S Fang H P 2014 Angew. Chem. Int. Ed. 53 10190
[45] Li H B Fang H P Lin Z F Xu S X Chen S Y 2004 Phys. Rev. 69 031919
[46] Chen J G Wang C L Wei N Wan R Z Gao Y 2016 Nanoscale 8 5676
[47] Wen B H Qin Z R Zhang C Y Fang H P 2015 Europhys. Lett. 112 44002
[48] Hopkins P Fortini A Archer A J Schmidt M 2010 J. Chem. Phys. 133 224505
[49] Lin B H Meron M Cui B X Rice S A Diamant H 2005 Phys. Rev. Lett. 94 216001
[50] Zeng X P Wu J B Li S B Chau Y Y He G H Wen W J Yang G Z 2014 Sci. China-Phys. Mech. Astron. 57 829