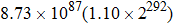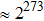Cite this Article
Liu Zeyu, Xia Tiecheng, Wang Jinbo. Image encryption technique based on new two-dimensional fractional-order discrete chaotic map and Menezes–Vanstone elliptic curve cryptosystem. Chinese Physics B, 2018, 27(3): 030502  
Permissions
Image encryption technique based on new two-dimensional fractional-order discrete chaotic map and Menezes–Vanstone elliptic curve cryptosystem
Liu Zeyu1, Xia Tiecheng1, †, Wang Jinbo2
Department of Mathematics, Shanghai University, Shanghai 200444, China
Science and Technology on Communication Security Laboratory, Chengdu 610041, China

 

† Corresponding author. E-mail: xiatc@shu.edu.cn

Abstract
Abstract

We propose a new fractional two-dimensional triangle function combination discrete chaotic map (2D-TFCDM) with the discrete fractional difference. Moreover, the chaos behaviors of the proposed map are observed and the bifurcation diagrams, the largest Lyapunov exponent plot, and the phase portraits are derived, respectively. Finally, with the secret keys generated by Menezes–Vanstone elliptic curve cryptosystem, we apply the discrete fractional map into color image encryption. After that, the image encryption algorithm is analyzed in four aspects and the result indicates that the proposed algorithm is more superior than the other algorithms.

PACS: 05.45.Ac;05.45.Df;05.45.Gg
Keyword:chaos;fractional two-dimensional triangle function combination discrete chaotic map;image encryption;Menezes-Vanstone elliptic curve cryptosystem
1. Introduction

Accompanied with the studying of discrete dynamic behavior, its applications have attracted a great deal of attention in secure communication field and a lot of work has been done in recent years.[1–9] For example, Li and Chen[10] have found that the fractional-order Chen system behaves chaotically. The hyperchaotic Lorenz system and Lorenz system have been modified into fractional order one[11,12] and applied in image encryption based on their fractional-order chaotic behavior. Compared with the fruitful results of image encryption utilizing the chaos of continuous fractional calculus, few works have referred to the discrete fractional calculus (DFC) and its applications.

The fractional difference was studied theoretically by Miller and Ross in 1989 as a groundbreaking work,[13] and the fractional integral was given as a fractional integral summation. After that, the theory of the fractional difference equations on time scales was developed.[14] For example, Atici and Eloe focused on the initial value problem,[15] Atici and Senguel referred to the discrete calculus of variations,[16] Holm proposed the Laplace transform[17] and Ortigueira et al. studied signal processing based on the discrete-time derivatives.[18,19] In recent years, Wu et al.[20–22] contributed on the applications of the discrete fractional calculus on an arbitrary time scale, theories of delta difference equations were used to reveal the discrete chaos behavior.

Elliptic curve cryptography (ECC) is an increasingly popular method for securing data and communication via public key encryption. ECC[23,24] has some advantages such as less computing, small storage capacity, and narrow bandwidth. Many public-key algorithms, such as Diflle–Hellman, EIGamal, and Schnorr, can be implemented in elliptic curves over finite fields. While sub-exponential algorithms can solve the integer factorization problem, only exponential algorithms are known for the elliptic curve discrete logarithm problem (ECDLP), so the ECC can achieve the same level of security with smaller key sizes and higher computational efficiency.[25] The Menezes–Vanstone elliptic curve cryptosystem (MVECC) is one of the famous elliptic curve public-key cryptosystems.[26]

Inspired by the work of the discrete dynamics behaviors,[27,28] one of the main goals is to introduce applications of the discrete fractional calculus on an arbitrary time scale[15,16,29] and to expose the discrete chaos behaviors of the fractionalized chaotic map by taking advantage of the theories of delta difference equations.

With the rapid development of transmitting images on the internet and information hiding, information security has attracted a great deal of attention in recent years. Image encryption is one of the widely used methods to protect image information, which can be implemented in optics and has become a more and more popular research area, nowadays. Many encryption methods within fractional derivatives have been proposed in recent years, such as the fractional-order hyperchaotic Lorenz system,[11] fractional-order Lorenz systems,[12,30] fractional-order Chen chaotic system,[31] synchronization of fractional chaotic systems[32] and delayed fractional-order chaotic logistic system.[33]

In Refs. [34]–[36], a new image encryption method based on fractional chaotic time series within the fractional-order difference was proposed, while the two-dimensional chaotic map within the fractional-order difference has seldom been proposed in color image encryption. It is well known that one-dimensional chaotic maps have the advantages of simplicity and high efficiency.[37] While the proposed two-dimensional fractional-order chaotic map can be converted into a more robust algorithm in image encryption due to more parameters being added in the equations.

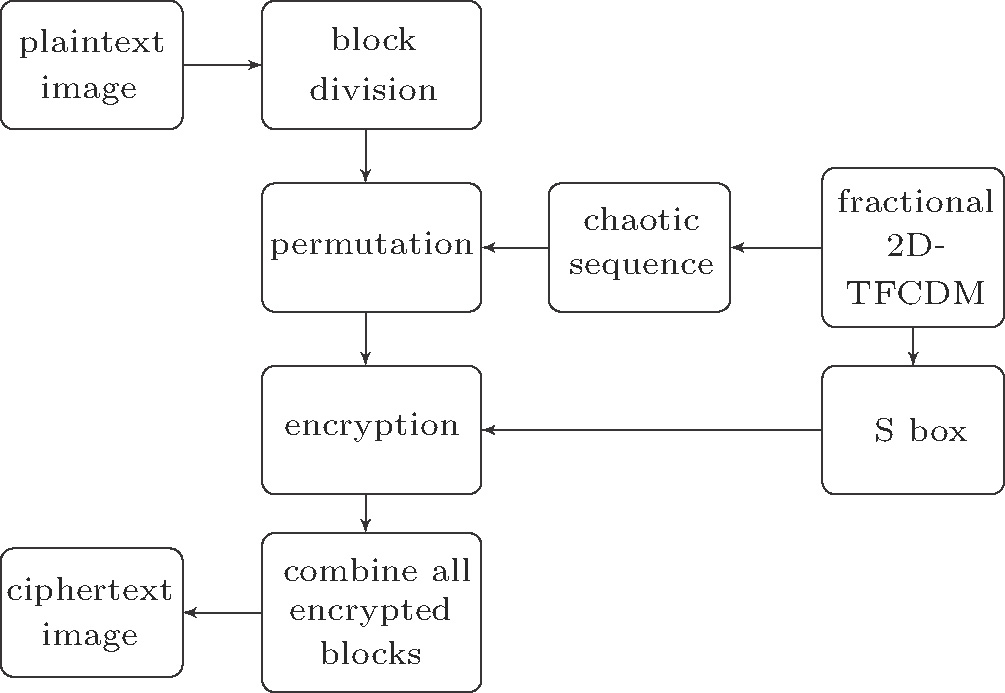
The main purpose of this paper is to introduce a new discrete two-dimensional fractional-order map and detect its chaos behaviour. In addition, we apply the map into the color image encryption and decryption with the keys enciphered by MVECC. This paper has eight sections: the definitions and the properties of the DFC are introduced in section 2. In section 3, we give the introduction of ECC and the operations on it, and then, the description of MVECC is given in the next section. In section 5, the fractional 2D-TFCDM on time scales from the discrete integral expression is given. The bifurcation diagrams, the largest Lyapunov exponent plot, and the phase portraits of the map are also displayed with different difference orders and initial points. After that, we give the application in the color image encryption. In section 7, the results in image encryption in section 6 are analyzed by commonly used methods. In the last Section, some conclusions are given.

2. Preliminaries

Let us briefly recall the fractional calculus definitions firstly. The definitions of the fractional sum and difference are given as follows. Within the DFC, the function f(t) is changed as a sequence f(n). Let denotes the isolated time scale and ( fixed). The difference operator is defined as .

3. Introduction to elliptic curve
3.1. Elliptic curve operations

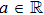
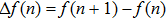
Let P = (x, y), then the negative of the point P is 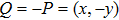where P + Q = O.[40]

If points and lie on an elliptic curve E defined in Eq. (7), then the sum P + Q results a third point R which also lies on E. Their sum is given as follows:[40] where and

The scalar multiplication is defined as where k is an integer.

4. Menezes–Vanstone elliptic curve cryptosystem

MVECC is a cryptosystem that uses the elliptic curves for “masking”, the plaintexts and ciphertexts are allowed to be arbitrary pairs of (nonzero) elements (i.e., they are not required to be points on 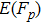), it makes MVECC a more efficient technique than ElGamal technique.[41]

If user A wants to encrypt and send message M to user B, then they go through the following steps:

1) User A and user B make an agreement on an elliptic curve and the base point α.

2) User B selects a private key k firstly and generates a public key γ = kα ( ).

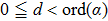
3) When user A wants to send a message to user B, he chooses a random private key d ( ), and then computes his public key β = dα. On the other hand, user A computes the secret key (c1, c2) by After that, he calculates the ciphered message by

4) The ciphertext is sent to user B. When user B wants to decrypt the ciphertext firstly, he computes the secret key by , then computes the following equations: to obtain the plaintext .[25]

Any adversary who only knows β and γ without the private keys d and k will find tht it is very difficult to solve the ECDLP to get the plaintext x. What is more, if # E has only one big prime divisor, the EC is called a secure EC.[40] Hence, MVECC is an efficient and secure technique.

5. Fractional 2D-TFCDM

From the fractional calculus,[20–22] we notice the application of the DFC to fractional generalizations of the discrete chaotic maps. In a recent paper,[42] the following 2D-TFCDM was introduced: which can be written into the form

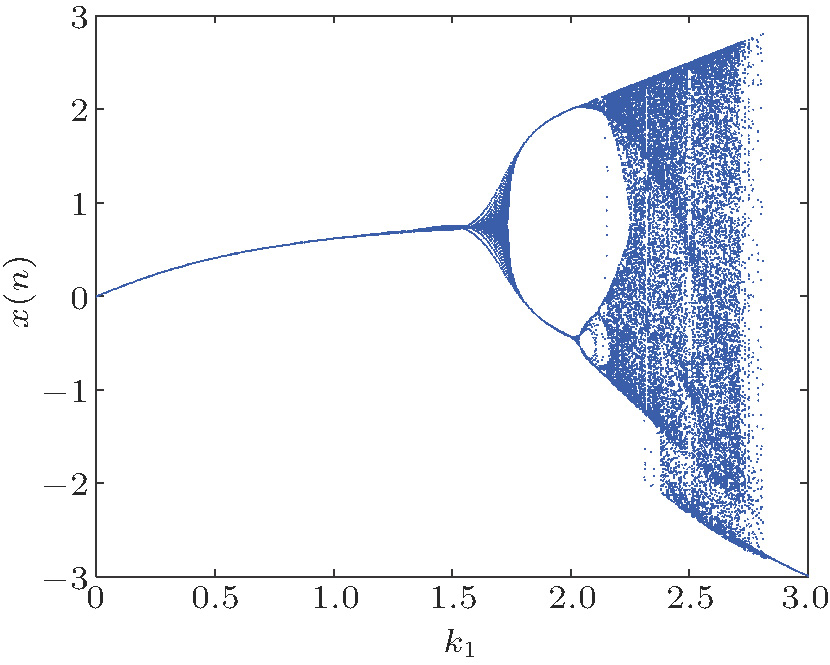
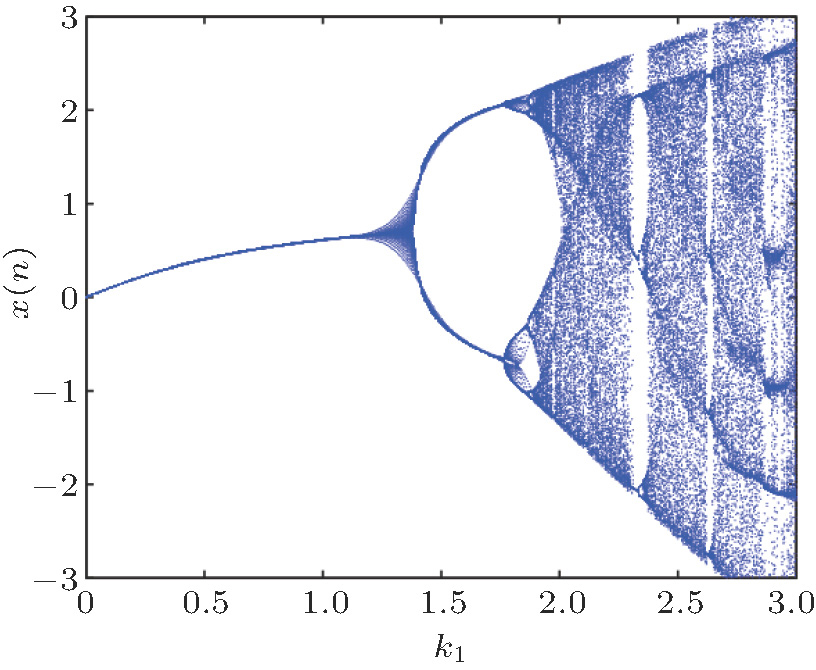An explicit numerical formula of equation (19) can be given as the bifurcation diagram, the largest Lyapunov exponent plot are given in Figs. 1–4.

Fig. 1. (color online) The bifurcation diagram of the 2D-TFCDM of variable k1 for ν = 1.
Fig. 2. (color online) The bifurcation diagram of the fractional 2D-TFCDM of variable k1 for ν = 0.8.
Fig. 3. (color online) The largest Lyapunov exponent of the 2D-TFCDM of variable k1.
Fig. 4. (color online) The largest Lyapunov exponent of the fractional 2D-TFCDM of variable k1 for ν = 0.8.

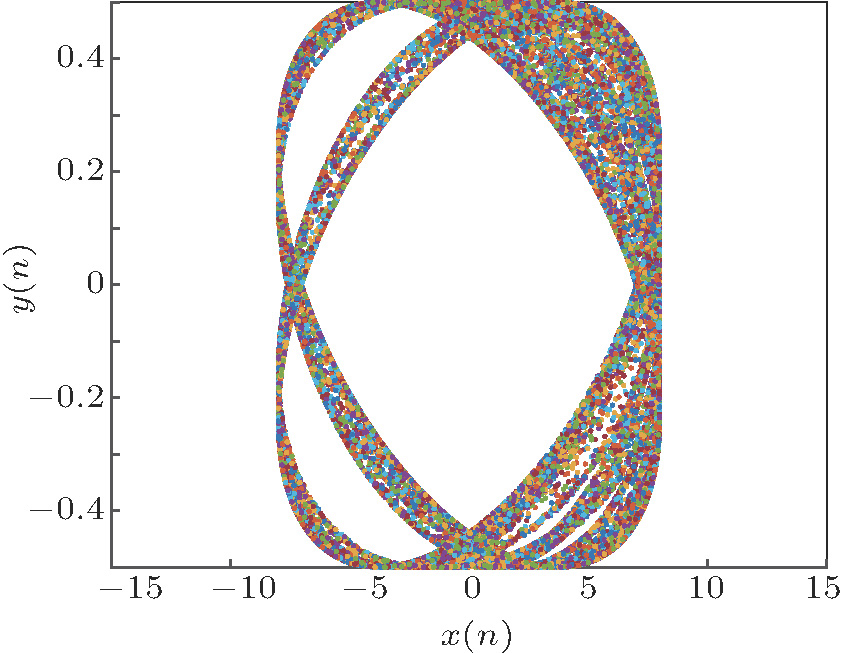
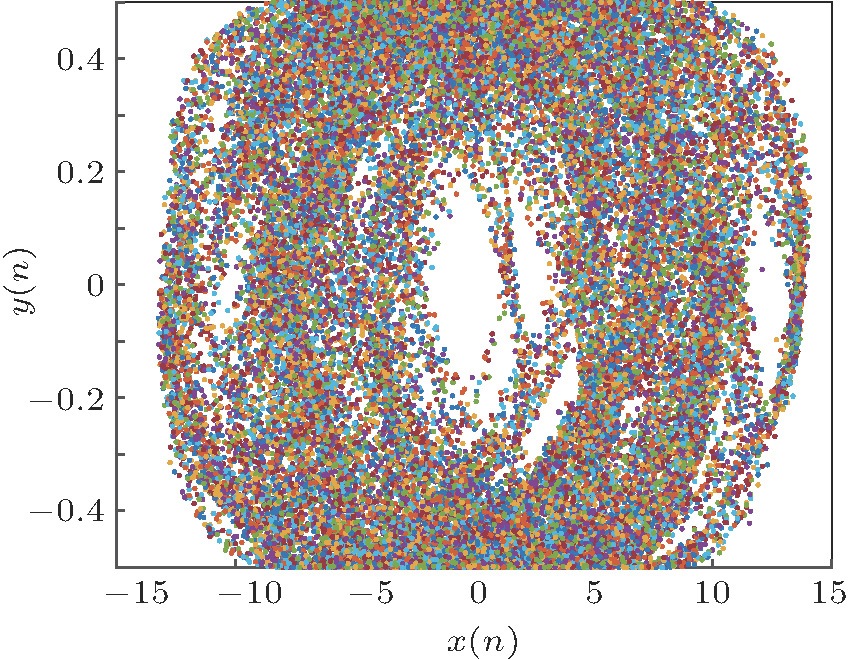
We choose 201 different initial values and derive the phase portraits of the integer map in Fig. 5. After that, more general chaos of the map is considered with the fractional difference order ν = 0.8 and ν = 0.6 in Figs. 6 and 7.

Fig. 5. (color online) The phase portraits of the 2D-TFCDM for k1 = 8, k2 = 0.5, and ν = 1.
Fig. 6. (color online) The phase portraits of the 2D-TFCDM for k1 = 8, k2 = 0.5, and ν = 0.8.
Fig. 7. (color online) The phase portraits of the 2D-TFCDM for k1 = 8, k2 = 0.5, and ν = 0.6.
6. Applications

The fractionalized chaotic map can also be applied in information security fields. Exploit Eq. (17) to be an algorithm, set the initial values x0, y0, the order ν and the coefficients k1, k2 of the chaotic system as keys for R, G, B components, respectively. The encryption algorithm proposed in this paper is divided into three parts.

6.1. Generation of new keys based on an elliptic curve in a finite field

Suppose that E is an elliptic curve defined over F100363 with parameters a = 1,b = 6 in Eq. (7). Since #E = 100801 is a prime, obviously, according to Ref. [40], it is a safe elliptic curve. Set , α = (2,4),d = 3565, then dα = (91292,60309)=β, the secret key k = 2513, , γ = kα = (73187,17539), ν = 2.382985485, and then the ciphertext is ((73187,17539),7123,45600), calculate . x0 = 9.8392, y0 = 5.5268, k1 = 0.6809, k2 = 9.2569, set , , , , then Set , , , , then , , , , are taken as the keys of the next step encryption.

6.2. Permutation procedure based on fractional 2D-TFCDM

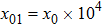
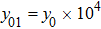
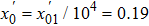
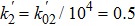
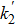
By using Eq. (17), utilizing , , , , and as the keys, we can obtain the encrypted figure.

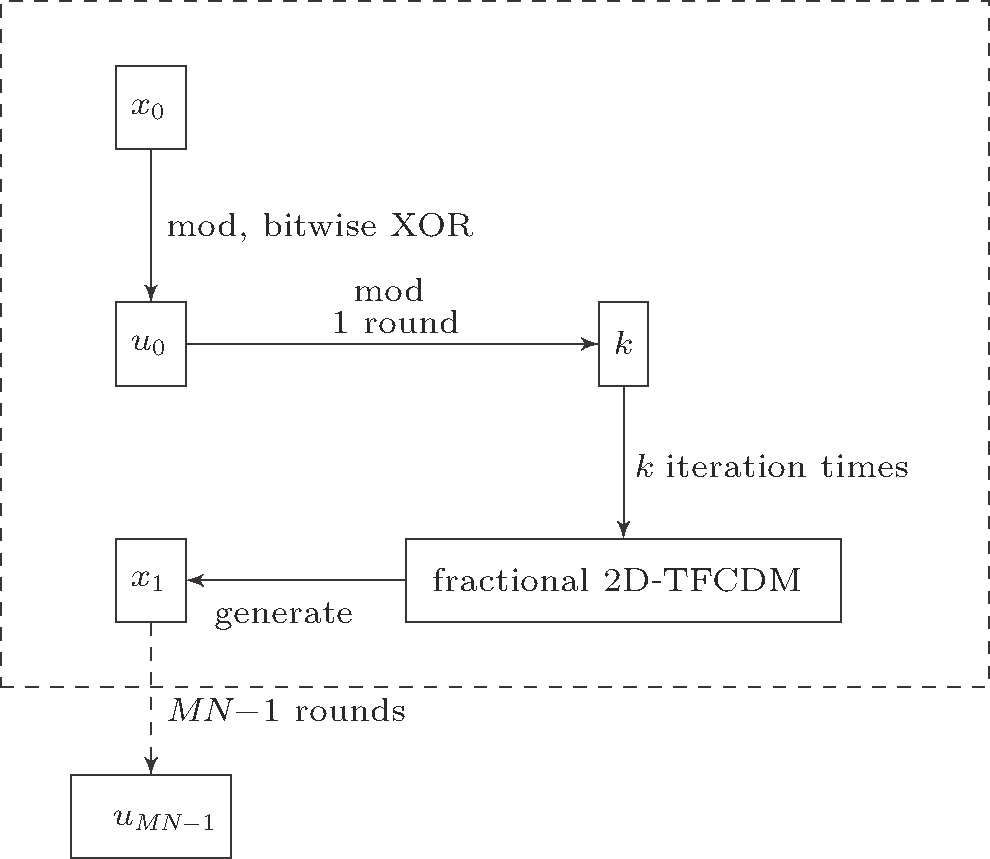
The procedure of permutation can be subdivided into the following four steps:

1) Set x0 equal to x(1), do an iteration operation for 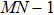times by using Eq. (17), here M and N represent length and width of the original picture V, respectively. Generate the one-dimensional real number chaotic sequences x(i), .

2) Reorder x(k) by the bubble sort to get , record the change of the subscript of x(k) as z(k).

3) Change the M × N original picture V into 1 × MN sequence v(k), reorder v(k) the same as x(k) according to z(k) then get .

4) Change 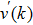into m × n figure as , the is the encrypted figure we needed.

By reversing this process, we can decrypt to obtain the original figure.

6.3. Encryption method based on fractional 2D-TFCDM

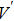
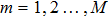
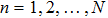
1) Do all permutation steps in Section 6.2 to generate the chaotic sequence x(i) and image . Change M × N original picture into 1 × MN sequence u(i), that i = N(m − 1) + n, ( , ). Another M × N image is used as a key image (K-image). Change the K-image into 1 × MN sequence w(i) as well.

2) Set i = 0.

3) Retain only the integer part of as , do modulus operation between and 256 as described in the following:

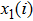
4) Consider the following formula: where is the XOR operation and represents the encrypted pixel value. The inverse form of Eq. (21) is

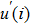
5) Compute the number k according to then, iterate the chaotic map k(i) times to get the new x(i + 1), return to step 3), until i = MN.

6) Change into an M × N figure as , the is the finally encrypted figure.

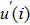
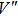
The decryption procedure has two parts as follows:

I) Do the same step in the encryption process until the step 4) is changed into Eq. (22).

II) Reverse the procedure in section 6.2 to remove the permutation effect.

Figure 8 displays the process of encryption in Sections 6.2 and 6.3. The working principle of the S box is illustrated in Fig. 9. The original, encryption, and decryption of an image are shown in Figs. 10–17. The width and height of some original images are not equal.

Fig. 8. The proposed encryption method.
Fig. 9. The S box.
Fig. 10. (color online) Pine. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 11. (color online) Lena. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 12. (color online) Yacht. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 13. (color online) House. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 14. (color online) Cornfield. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 15. (color online) Tiffany. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 16. (color online) Ground. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 17. (color online) Island. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.

In the process of encryption and decryption of Section 6.1, the keys are different, however, in Section 6.2, they are the same.

7. Analysis of results in applications
7.1. Key space

In the algorithm proposed in this paper, the initial values x0, y0, the order ν, and the coefficients of chaotic system k1, k2 can be used as the secret keys, so there are five secret keys. Assume that the precision of x0 and y0 is 2 × 10−17 and 3 × 10−17, respectively. Similarly, the secret keys are added 6 × 10−17, 8.9 × 10−16, 6 × 10−17 to decrypt the encrypted images, respectively. The secret keyʼs space is . When the size of the original image is 512 × 512, the key space of the K-image is 256 × 256 × 28 = 224. The key space is 1.10 ×2292 in total.

7.2. Statistics analysis

The statistical property is significant to an encrypted image, a good encryption method should be robust against any statistical attack.

7.2.1. Correlation of the plain and cipher images

In an ordinary image, the correlation coefficient of adjacent pixels is usually high for the reason that the adjacent pixels values are close. A good encryption algorithm should make the correlation of adjacent pixels nearly equal to zero. The closer to zero the correlation coefficients are, the better the encryption algorithm is. The correlation coefficients are calculated according to and the results are displayed in Table 1. The correlation along the x direction of the original and the encrypted figure from Sailboat to Tiffany are shown in Figs. 18–25.

Fig. 18. (color online) Analysis of the correlations of Pine (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
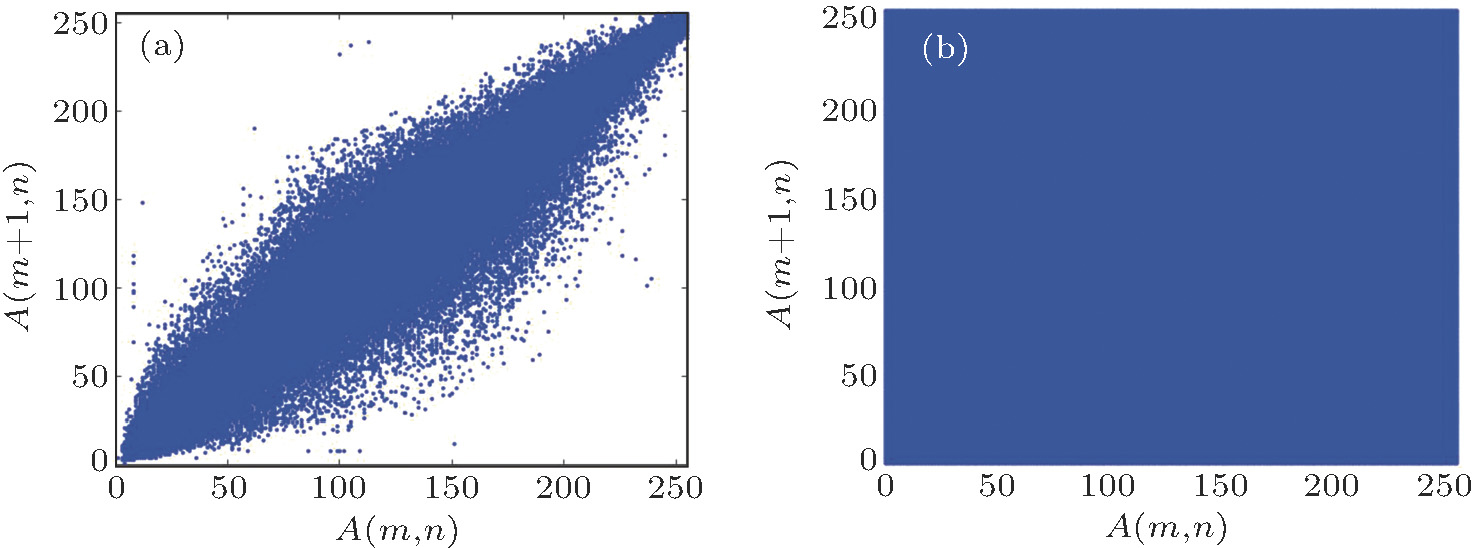Fig. 19. (color online) Analysis of the correlations of Lena (x-direction). (a) Plain image (x direction); (b) encrypted image (x direction).
Fig. 20. (color online) Analysis of the correlations of Yacht (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
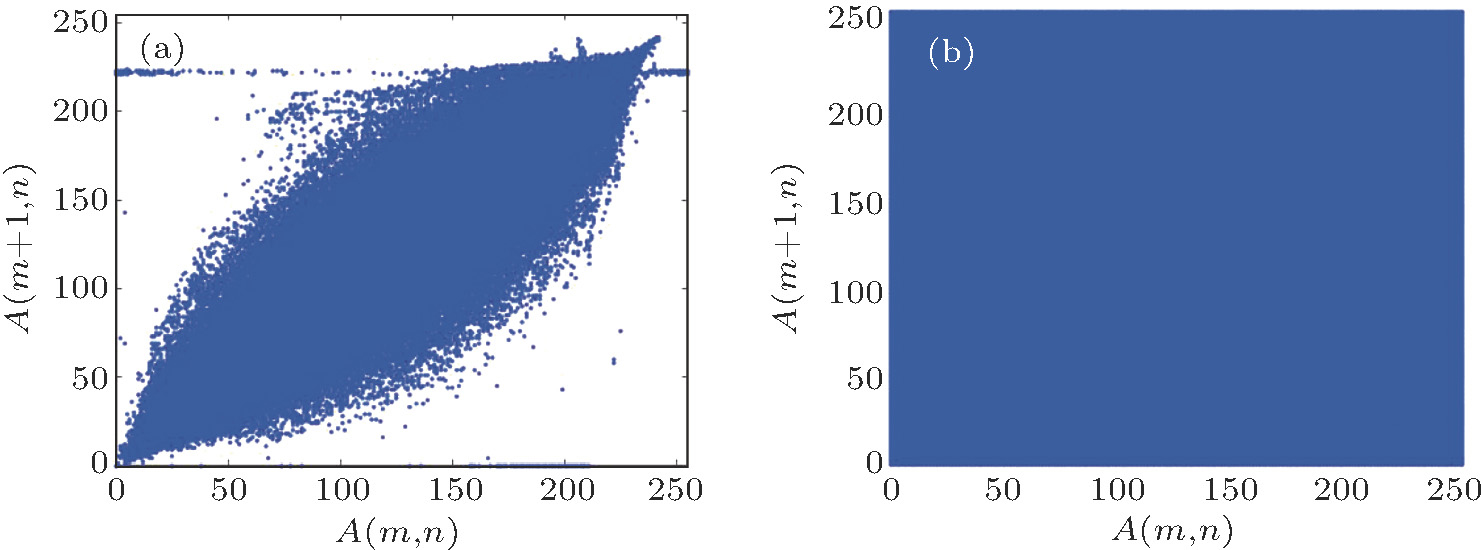Fig. 21. (color online) Analysis of the correlations of House (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
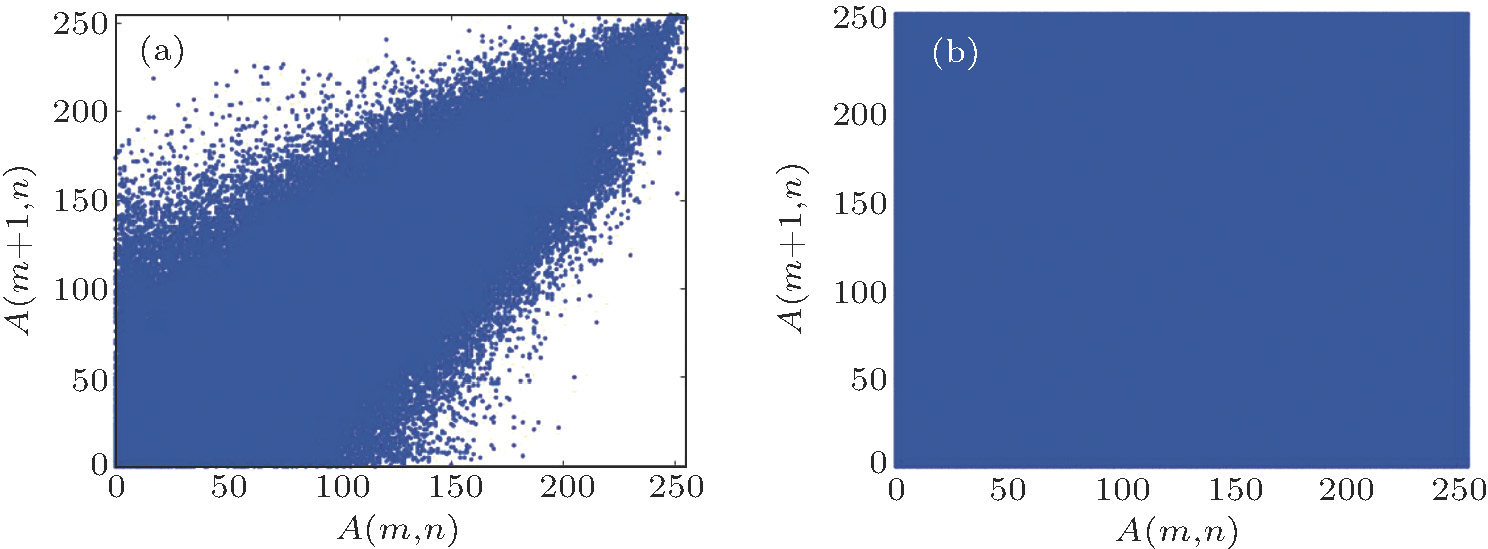Fig. 22. (color online) Analysis of the correlations of Cornfield (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
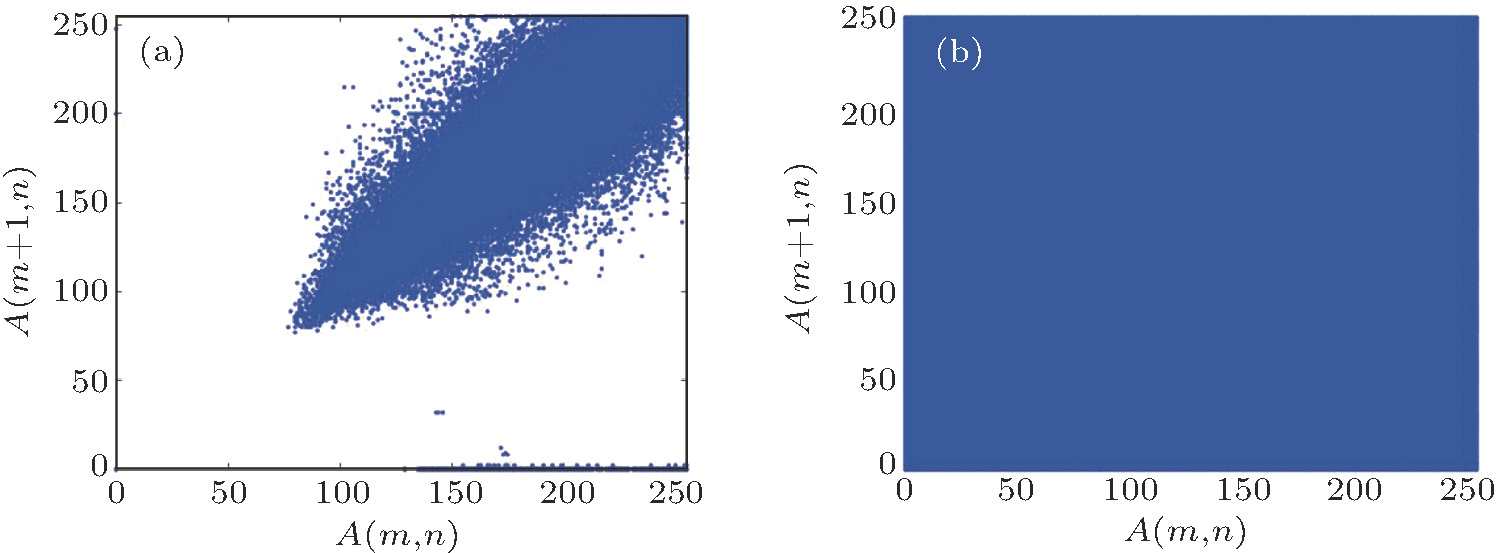Fig. 23. (color online) Analysis of the correlations of Tiffany (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
Fig. 24. (color online) Analysis of the correlations of Ground (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
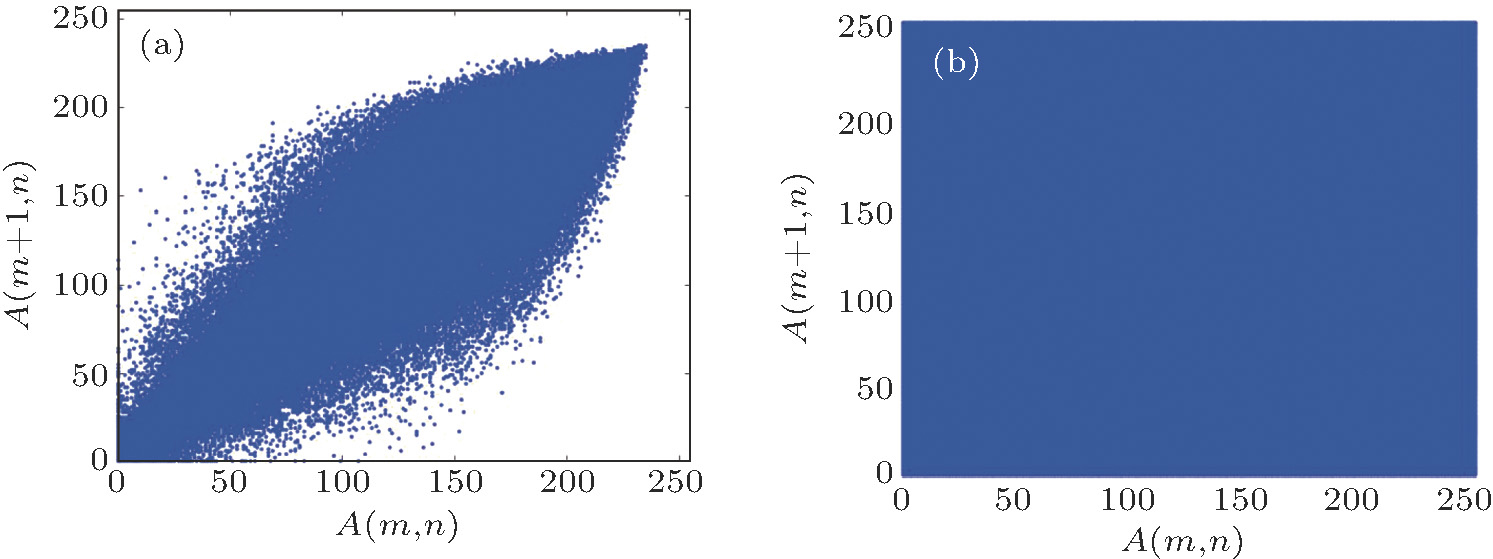Fig. 25. (color online) Analysis of the correlations of Island (x direction). (a) Plain image (x direction); (b) encrypted image (x direction).
Table 1.

Correlation coefficients of image.

.

Obviously, the correlation of the original image has a linear relationship, however, the encrypted image is stochastic. We can find in Table 1 that the correlation coefficients of the encrypted image are nearly equal to 0. The correlation coefficients of the original image are all larger than 0.9, which indicates a high relativity between the two adjoining pixels. It shows that the encryption process make the pixels of the image almost independent of each other.

From Table 2, we can observe that most correlation coefficients of an encrypted image are more near to 0 than the one in other work. In consequence of this, the proposed encryption algorithm is superior to other methods.

Table 2.

Comparison of correlation coefficients of image.

.
7.2.2. Histogram

The distribution of colors inside the image is shown by a histogram. The adversary can obtain some effective information from the regular histogram. Therefore, an encrypted image should be uniformly distributed in an image encryption method with good encryption effect. Figure 26 shows the histogram of Pine. Similarly, the histograms of seven other cases are shown in Figs. 27–33.

Fig. 26. (color online) The histogram of Pine. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 27. (color online) The histogram of Lena. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
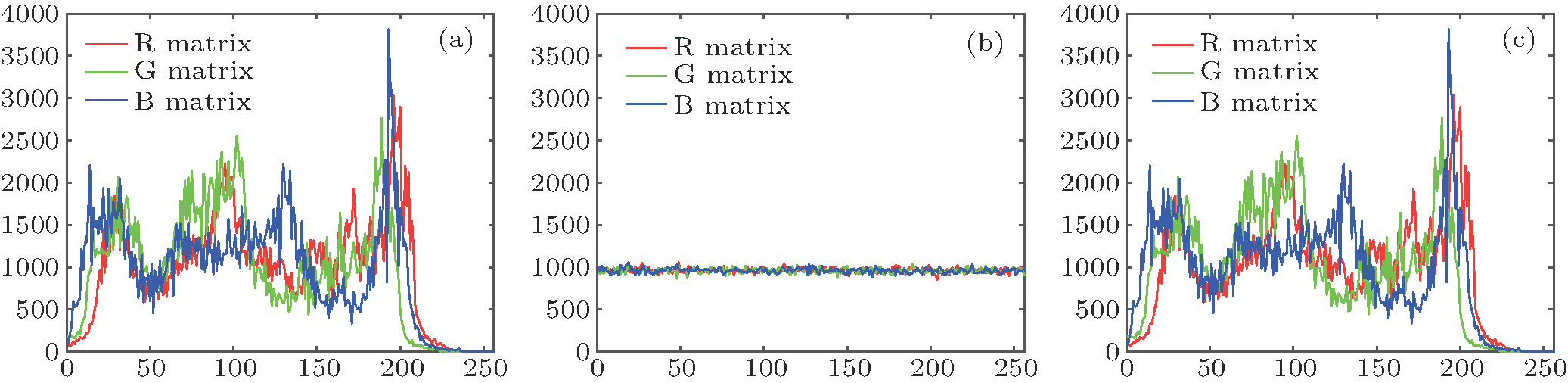Fig. 28. (color online) The histogram of Yacht. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 29. (color online) The histogram of House. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 30. (color online) The histogram of Cornfield. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 31. (color online) The histogram of Tiffany. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 32. (color online) The histogram of Ground. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
Fig. 33. (color online) The histogram of Island. (a) The original figure, (b) the encrypted figure, and (c) the decrypted figure.
7.2.3. Information entropy

Entropy is a measure of unpredictability of information content. The information entropy is the most important feature of randomness and can be used to measure the degree of uncertainty of a system. It is defined as where expresses the probability of symbol mi and n is the number of bits that is required to represent the symbol. When the pixel values of an image are in the range of 0–255, according to Eq. (28), the ideal information entropy is 8 bits for an ideally random image. Therefore, the closer to 8 bits the information entropy is, the better the encryption scheme is. The data of the information entropy are shown in Table 3. The result means that the encrypted images are very close to the random images.

Table 3.

Information entropy.

.

In Table 4, we can find that the information entropy of encrypted Lena of the proposed algorithm is closer to 8 than other algorithms.

Table 4.

Comparison of information entropy.

.
7.3. Sensitivity analysis

The different range between two images can be measured by two criteria: number of pixels change rate (NPCR) and unified average changing intensity (UACI). They are defined as Here, W and H represent the width and height of the image, respectively, and T1 and T2 represent the two images to be analyzed.

7.3.1. Key sensitivity

We encrypt the image by using the keys x0 = 0.19, y0 = 0.06, ν = 0.7123456, k1 = 8, and k2 = 0.5. Figure 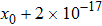34(a) represents the normally recovered image. Figure 34(b) decrypts the encrypted image using with other correct secret keys, but it failed. The decrypted image is apparently different from the original image. Similarly, the secret keys are added separately to decrypt the encrypted images. The results are shown in Figs. 34(c)–34(f). Table 5 lists the key space of the proposed algorithm and other algorithms as a comparation. The NPCR and UACI between Figs. 34(a) and Figs. 34(b)–34(f) are calculated in Table 6, respectively.

Fig. 34. (color online) The test of key sensitivity. (a) The normally recovered image, (b) , (c) , (d) , (e) , and (f) .
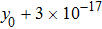
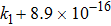
Table 5.

Comparison of key spaces.

.
Table 6.

NPCR and UACI between Figs. 34(a) and Figs. 34(b)–34(f).

.

In contrast with other algorithms, the key space of the proposed algorithm is larger.

It can be observed from Table 6 that all NPCR are higher than 90% and most of UACI are higher than 30%. We cannot recognize the object inside Figs. 34(b)–34(f), so that the encryption method is sensitive to the secret keys.

7.3.2. Plaintext sensitivity

By encrypting two original images with one pixel difference and comparing the two encrypted images, the attackers can obtain effective information. A good encryption method should ensure that the two encrypted images are completely different even if there is only one pixel difference.

The results are shown in Tables 7–14, Figure 10(a)(x,y) indicates that the pixel value of coordinate (x,y) is different from the pixel values in the same position as that in Fig. 10(a), and it was set as the original image. After encryption, the NPCR and UACI are calculated according to Eqs. (30) and (31).

Table 7.

NPCR and UACI between cipher-images with slightly different plain-images (Pine).

.
Table 8.

NPCR and UACI between cipher-images with slightly different plain-images (Lena).

.
Table 9.

NPCR and UACI between cipher-images with slightly different plain-images (Yacht).

.
Table 10.

NPCR and UACI between cipher-images with slightly different plain-images (House).

.
Table 11.

NPCR and UACI between cipher-images with slightly different plain-images (Cornfield).

.
Table 12.

NPCR and UACI between cipher-images with slightly different plain-images (Tiffany).

.
Table 13.

NPCR and UACI between cipher-images with slightly different plain-images (Ground).

.
Table 14.

NPCR and UACI between cipher-images with slightly different plain-images (Island).

.

The ideal values of NPCR and UACI are 99.61% and 33.46%, respectively.[43] From Table 15, it is calculated that the NPCR and UACI of the proposed algorithm are nearer to the ideal values than other algorithms.

Table 15.

Comparison of NPCR and UACI.

.
7.4. Resistance to known-plaintext and chosen-plaintext attacks

In section 6.3, the iteration times of the next round are determined by the last round encrypted image pixel. In Eq. (21), x2(i), produced by the fractional 2D-TFCDM, is dependent on the iteration times k(i−1) and decides the iteration times k(i). Consequently, the corresponding keystream is different when different plaintexts are encrypted. For the resultant information is related to those chosen-images, the attacker cannot obtain useful information by encrypting some special images. As a result, the attacks proposed in Refs. [44]–[46] are ineffective on the new scheme. While, the proposed scheme can primely resist the known-plaintext and the chosen-plaintext attacks.

8. Conclusions

In this paper, the fractional 2D-TFCDM was obtained from the 2D-TFCDM and new chaotic dynamics behaviors with the proposed map were found. We also found that the map can be applied in color image encryption and decryption. Finally, the encryption algorithm was analyzed in four aspects. The proposed algorithm is superior to others in almost all aspects.

Reference
[1] Chai X L Gan Z H Lu Y Zhang M H Chen Y R 2016 Chin. Phys. 25 100503
[2] Chai X L Gan Z H Yuan K Lu Y Chen Y R 2017 Chin. Phys. 26 020504
[3] Ye G D Huang X L Zhang L Y Wang Z X 2017 Chin. Phys. 26 010501
[4] Xu L Gou X Li Z Li J 2017 Opt. Laser. Eng. 91 41
[5] Teng L Wang X Y Meng J 2017 Multimedia Tools Appl. 1
[6] Enayatifar R Abdullah A H Isnin I F Altameem A Lee M 2017 Opt. Laser Eng. 90 146
[7] Li Y Wang C Chen H 2017 Opt Laser Eng 90 238
[8] Ismail S M Said L A Rezk A A Radwan A G Madian A H Abu-ElYazeed M F Soliman A M 2017 IEEE The 6th International Conference on Modern Circuits and Systems Technologies pp. 1–4 https://doi.org/10.1109/MOCAST.2017.7937642
[9] Zhao J F Wang S Y Zhang L T Wang X Y 2017 J. Electr. Comput. Eng. 2017 8672716
[10] Li C Chen G 2004 Physica 341 55
[11] Wang Z Huang X Li Y X Song X N 2013 Chin. Phys. 22 010504
[12] Radwan A G Abd-El-Hafiz S K AbdElHaleem S H 2012 IEEE, International Conference on Engineering and Technology (ICET)
[13] Miller K S Ross B 1988 Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and their Applications
[14] Bohner M Peterson A 2012 Dynamic Equations on Time Scales: An Introduction with Applications Springer
[15] Atici F M Eloe P W 2009 Proc. Am. Math. Soc. 137 981
[16] Atici F M Sengul S 2010 J. Math. Anal. Appl. 369 1
[17] Holm M T 2011 Comput. Math. Appl. 62 1591
[18] Ortigueira M D Coito F J V Trujillo J J 2013 IFAC Proceedings Volumes 46 629
[19] Ortigueira M D 2000 IEEE, Proceedings-Vision, Image and Signal Processing 147 71
[20] Wu G C Baleanu D Zeng S D 2014 Phys. Lett. 378 484
[21] Wu G C Baleanu D 2015 Nonlinear Dyn. 80 1697
[22] Wu G C Baleanu D 2014 Nonlinear Dyn. 75 283
[23] Koblitz N 1987 Math. Comput. 48 203
[24] Miller V S 1985 Conference on the Theory and Application of Cryptographic Techniques Berlin, Heidelberg Springer
[25] Araki K Satoh T Miura S 1998 International Workshop on Public Key Cryptography Berlin, Heidelberg Springer
[26] Ma C 2014 National Defense Industry Press
[27] Yan Z Y 2005 Phys. Lett. 342 309
[28] Yan Z Y 2006 Chaos 16 013119
[29] Atici F M Eloe P W 2007 Int. J. Differ. Equ. 2 165
[30] Paral P Dasgupta T Bhattacharya S 2014 International Conference on Communications and Signal Processing ICCSP
[31] Wu X Li Y Kurths J 2015 PloS One 10 e0119660
[32] Xu Y Wang H Li Y Pei B 2014 Commun. Nonlinear Sci. Numer. Simulat. 19 3735
[33] Wang Z Huang X Li N Song X N 2012 Chin. Phys. 21 050506
[34] Wu G C Baleanu D Lin Z X 2016 J. Vib. Control. 22 2092
[35] Liu Z Y Xia T C 2017 Appl. Comput. Inf. DOI:10.1016/j.aci.2017.07.002https://doi.org/10.1016/j.aci.2017.07.002
[36] Liu Z Y Xia T C Wang J B 2017 J. Vib. Control. DOI:1077546317734712 https://doi.org/10.1177/1077546317734712
[37] Elnashaie S S E H Abashar M E 1995 Chaos. Soliton. Fract. 5 797
[38] Abdeljawad T Baleanu D 2011 J. Comput. Anal. Appl. 13 574
[39] Chen F Luo X Zhou Y 2011 Adv. Differ. Equ. 2011 713201
[40] Xiao Y 2006 Research on Elliptic Curve Cryptography Wuhan Huazhong University of Science and Technology Press in Chinese
[41] Dawaheh Z E Yaakob S N Othman R R B 2016 J. Theor. Appl. Inf. Technol. 85 290
[42] Li P Min L Hu Y Zhao G Li X 2012 IEEE 6th International Conference on Information and Automation for Sustainability (ICIAfS)
[43] Guo F M Tu L 2015 The Application of Chaotic Theory in Cryptography Beijing Beijing Institute of Technology Press in Chinese
[44] Xiao D Liao X Wei P 2009 Chaos Soliton. Fract. 40 2191
[45] Li C Li S Chen G Halang W A 2009 Image Vision. Comput. 27 1035
[46] Rhouma R Solak E Belghith S 2010 Commun. Nonlinear Sci. Numer. Simulat. 15 1887