† Corresponding author. E-mail:
We show that the global monopole spacetime is one of the exact solutions of the Einstein equations by treating the matter field as a non-linear sigma model, without the weak field approximation applied in the original derivation by Barriola and Vilenkin. Furthermore, we find the physical origin of the topological charge in the global monopole spacetime. Finally, we generalize the proposal which generates spacetime from thermodynamical laws to the case of spacetime with global monopole charge.
The global monopole charge resulted from the breaking of global O(3) symmetry belongs to those eccentric objects like cosmic strings and domain walls, and plays an important role in modern physics.[1] Generally speaking, the global monopole charge is one kind of topological defect which can be produced by the phase transition in the early universe. There are a series of important investigations about this kind of topic before. For instance, Harari and Loustò found that the gravitational potential of such topological defect is negative;[2] the same topic in the d S/Ad S spacetime was explored in Ref. [3] and the scholars found that the gravitational potential can be either repulsive or attractive, depending on the value of the cosmological constant. In addition, a new class of cold stars called D-stars (defect stars) were proposed in Refs. [4]–[6], in which the authors argued that the theory has monopole solutions in the case that the matter field disappears. Besides, the global monopole charge has also been considered in cosmology, see Refs. [7]–[10] for more details. Moreover, the global monopole spacetime was first found by Barriola and Vilenkin in 1989[11] in which this category of spacetime was derived by applying the weak field approximation.
In Ref. [12], the general bulk/boundary correspondence, a generalized version of the Ad S/CFT correspondence, was proposed. In order to find the evidence to support their proposal, the authors put forward the thermodynamics on the bulk where the topological charge was constructed. However, it should be noted that the authors’ proposal of this new physical concept (namely the topological charge) was based on some mathematical tricks and the physical origin of the topological charge was missed in this proposal.
In this paper, we prove that the global monopole spacetime is an exact solution of the Einstein equations if the matter field is applied as the free nonlinear sigma model which has been introduced in Ref. [13]. Additionally, we show that our work can be applied to higher-dimensional spacetime as well as another maximum symmetrical spacetime. Furthermore, the difficulties in Ref. [12] are investigated in our work by showing that the physical background of the topological charge is the sigma model (either linear or non-linear one, depending on the topological structure of the spacetime), and this topological charge will be reconstructed in a more reasonable way inspired by Ref. [14].
This paper is organized as follows. In Section
In this section, we show that the global monopole spacetime can be derived as an exact solution of the Einstein equations if one applies the matter field as the non-linear sigma model. This section contains three parts, in part 1, the matter field is introduced; in part 2, a derivation of the global monopole spacetime is presented; in part 3, the general properties of the Lagrangian which could be applied to derive the global monopole spacetime are discussed.
As discussed before, the matter field is considered as the non-linear sigma model whose Lagrangian is
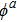
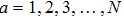
Applying the variational principle
The metric ansatz we apply here is
Furthermore, inspired by Ref. [14], we can construct the topological charge of this spacetime as
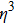
In this subsection, we would like to discuss a class of Lagrangian which could be used to derive the global monopole spacetime. To begin with, we choose the following ansatz for the Lagrangian:
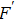
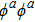
Following Ref. [11], we propose the ansatz of the scalar ϕa as
 |
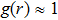
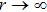
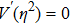
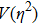
In this section, the method proposed above is generalized to more general cases. Firstly, it will be applied to higher-dimensional spacetime, and secondly, other classes of symmetrical spacetime with the global monopole charge will be derived.
In this case, the metric ansatz of the n-dimensional spacetime is
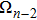
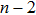
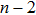
Besides, the matter field applied here is still the non-linear scalar field, meaning that equation (
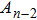
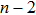
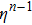
We derive the global monopole-like spacetime in the plane-symmetric case in this subsection. Firstly, we introduce the metric ansatz as
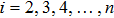
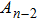
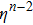
We apply our proposal to the hyperbolically symmetric case in this subsection, and the metric ansatz is
Using the Einstein equations (
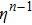
In Ref. [12], while the authors constructed the black hole thermodynamics with the topological charge in formula, it is interesting to investigate the matter field in the spacetime that plays an important role in the thermodynamics. In our proposal, we suggest that the matter field is the sigma model, and for convenience, we propose the first law of thermodynamics in the plane case as
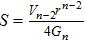
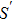
Indeed, there is a quasi-local version of such black hole thermodynamics, which is the so-called unified first law
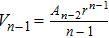
In the quasi-local version of thermodynamics, the quasi-local energy E can be defined as the so-called Misner–Sharp energy
Besides, there are a series of works which generate the spacetime construction from thermodynamics by using the unified law and treating the spacetime as an adiabatic system.[21–23] These works can be summarized as follow: one can derive the structure of the spacetime once there is a work term defined by Eq. (
There was a try before. In Ref. [24], the authors put forward a similar method by using the Komar mass and the ADM mass, rather than the Misner–Sharp mass to generate the spacetime from thermodynamics. In that work, the authors applied their proposal to the global monopole spacetime successfully. However, when they generated the global monopole spacetime, some subtle trick was applied, which may cause argument.
Here, we argue that the original method can be applied to the spacetime with the global charge exactly. We consider the plane case first and choose the metric ansatz for convenience as
Our next task is to find f(r). To do this, we need to apply the so-called geometric surface gravity, which was first proposed in Ref. [17] and generalized to higher-dimensional spacetime in Ref. [22], defined as
Here, we generalize the method that one can derive the spacetime structure from thermodynamics to the spacetime with global monopole charge, which is not the maximum symmetrical spacetime, and the topological charge plays a center role in the work term.
The global monopole spacetime was first presented in Ref. [11], in which the matter field is treated as an approximate one. Thus, one of our works is deriving this spacetime exactly and revealing that the matter field which can be used to derive this spacetime is the non-linear sigma model. Moreover, the derivation is also generalized to higher-dimensional spacetime (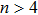
Our another work is that we reconstruct the topological charge which was first proposed in Ref. [12]. We find that the physical origin of the topological charge is the sigma model (both the linear one and the non-linear one). Moreover, our result can match the original proposal well in the plane-symmetric case, so it could be claimed that our work is an apposite generalization of the construction in Ref. [12].
Moreover, we investigate the thermodynamics of the spacetime by applying the Misner–Sharp energy in our discussion, and then we construct the unified first law for this class of spacetime. We propose that the global monopole spacetime can be generated from the unified first law.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |

