† Corresponding author. E-mail:
Separability is an important problem in theory of quantum entanglement. By using the Bloch representation of quantum states in terms of the Heisenberg–Weyl observable basis, we present a new separability criterion for bipartite quantum systems. It is shown that this criterion can be better than the previous ones in detecting entanglement. The results are generalized to multipartite quantum states.
Quantum entanglement is a fascinating phenomenon in quantum physics. In recent decades, much works have been devoted to understand entanglement as it plays important roles in many quantum information processing. Nevertheless, there are still many problems remain unsolved in the theory of quantum entanglement. One basic problem is to determine whether a given bipartite state is entangled or separable. Although the problem is believed to be a nondeterministic polynomial-time hard problem, there are a number of operational criteria to deal with the problem, for example, the positive partial transpose (PPT) criterion,[1,2] realignment criteria,[3–7] covariance matrix criteria,[8–10] correlation matrix criteria,[11–13] and so on. More recently, some more separability criteria have been proposed.[14–19] Among them, Li et al.[14] presented separability criteria based on correlation matrices and the Bloch vectors of reduced density matrices. By adding some extra parameters, reference [19] present a more general separability criterion for bipartite states in terms of the Bloch representation of density matrices.
The state of two quantum systems A and B, acting on the finite-dimensional Hilbert space 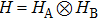
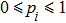
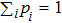
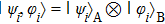

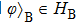
In this article, we put forward a new Bloch representation in terms of the Heisenberg–Weyl (HW) observable basis.[21] It is one of the standard Hermitian generalization of Pauli operators, constructed from HW operators.[22–25] They have distinct properties from those of Gell–Mann matrices,[21] Based on the Heisenberg–Weyl representation of density matrices, we give a new separability criterion for bipartite quantum states and multipartite states. By example, we show that this criterion has advantages in determining whether a quantum state is separable or entangled.
HW observable basis First, we briefly introduce the HW-operator basis.[21] The generalized Pauli “phase” and “shift” operators are given by 
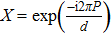
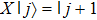
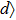
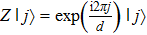
The phase-space displacement operators for d-level systems are defined by
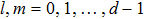
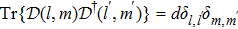
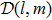
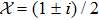
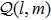
Note A brief guidance on how to prepare a manuscript is also given at the end of this template (after the Reference section).
A state 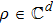
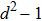
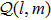
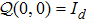
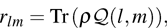 |
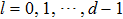
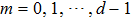

Proof According to Eq. (
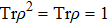

Now consider bipartite states 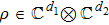
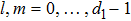
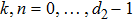
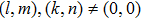
Similar to (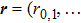
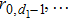
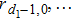
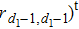
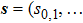
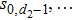
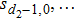
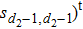
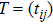
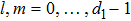
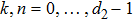
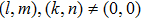
Let us consider the following matrix:
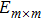
Proof Since ρ is separable, from Ref. [13] there exist vectors 
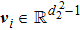
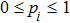
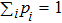
Accounting to that for any vectors 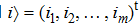
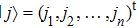
For high-dimensional quantum states, let us consider the following 2 × 4 bound entangled state[28] as an example:
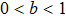
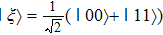
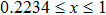
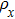
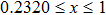
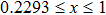
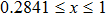
Here, instead of (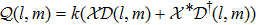
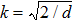
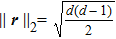
We now generalize our result in Theorem 
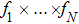

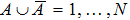

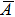
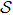
For any state ρ in 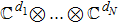
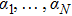
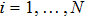

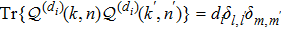
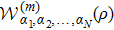
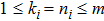
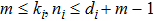
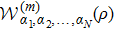
Proof Without loss of generality, we assume
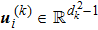
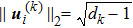
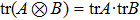
As for tripartite case, by taking m=1, and 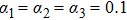
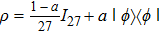

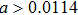

We have studied the separability problem based on the Bloch representation of density matrices in terms of the Heisenberg–Weyl observable basis. New separability criteria have been derived for both bipartite and multipartite quantum systems, which provide more efficient ways in detecting quantum entanglement for certain kinds of quantum states. These criteria can experimentally implemented.
In Ref. [19] the traceless Hermitian generators of SU(d) satisfying the orthogonality relations have been used in the Bloch representation of density matrices. While in this paper we have adopted the same approach as the one used in Ref. [19] but used the Heisenberg–Weyl observable basis[21] in the Bloch representation of density matrices. An interesting fact here is that the ability of detecting quantum entanglement can be improved by using different observable basis in the Bloch representation. Hence our results are complementary to the ones obtained in Ref. [19] in detecting entanglement for some quantum states. Just like the case that one needs different witnesses to detect the entanglement of different quantum states, we need to measure the quantum systems with suitable local observable sets in entanglement detection. The choices of suitable observable basis depend on the detailed entangled states to be detected. It would be more interesting if such state-dependent choices of observable basis can be analytically derived optimally. It is also possible to improve such separability criteria by taking into account measurement outcomes of more observable bases simultaneously, similar to the cases that involve all the mutually unbiased bases,[32,33] or mutually unbiased measurements,[34] or general symmetric informationally complete positive operator-valued measurements.[35]
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |

