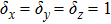Genes are the carriers of genetic information, and the expression of genes is the basic process of life system. Many genes and proteins are involved in the life process and they constitute rather complicated regulatory networks. Although regulatory networks are very complex, recent research has shown that these complex gene regulatory networks can be decomposed into many typical small network motifs, such as auto-regulation motifs, feedback motifs, feed-forward loops, etc.^[1]

Random fluctuations in gene transcriptional regulatory networks are unavoidable, as whether chemical reactions occur is probabilistic and the numbers of many genes, RNAs and proteins are all small in each cell.^[2] Noise and fluctuations have permeated into all levels of the biological system, from the basic molecular, sub-cellular processes to the kinetics of tissues, organs, organisms and populations.^[3] There is a large amount of random noise in DNA replication, transcription regulation and protein translation in organisms. It is very well known that the internal noise and the external noise are both inevitable in a biochemical reaction system.^[4–6] The internal noise that comes from stochastic fluctuations of random chemical reaction events^[7–10] in biochemical systems can result in gene mutation and evolution,^[11] cell-to-cell variability,^[7,12,13] and even different observable phenotypes.^[11]

A large number of motifs exist in the gene transcription regulatory networks, i.e., auto-regulation motif, feedback motif, feed-forward loop. We can find that the number of units that make up these simple modules is relatively few, so the noise should not be ignored. It is recognized that feedback loops and noise play important roles in a wide variety of biological processes, such as galactose regulation,^[14] calcium signalling,^[15,16] p53 regulation,^[17] cell cycle,^[18,19] and cell fate decision in budding yeast.^[20,21] Some studies indicated that positive feedbacks tended to magnify noise and negative feedbacks typically attenuated noise.^[22–24] However, most of the positive feedback loops are bistable where stationary noise in a real system is rarely observed, and only transition rate can be measured. The difficulty in predicting the transition rate lies in the fact that noise and transient kinetics (e.g. due to step-response) have often similar effects on transition rate and it is difficult to distinguish between them. Some researchers have pointed out that the gene expression noise is a key factor in determining the rate of transition in the bistable range.^[25] Nevertheless, other studies have shown that the positive feedbacks can attenuate noises and strong correlation does not exist between the feedback signals (negative or positive) and the noise attenuation characteristic.^[26,27]

As typical of biological motif, the feed-forward loop consists of two input transcription factors and a target gene. One of the transcription factors regulates the other, conjointly regulating the target gene. Each of the transcription interactions among three genes in the feed-forward loop can be either activation (positive) or inhibition (negative), therefore the feed-forward loop has eight possible structural types with different activation and repression interactions. According to the different regulatory functions between direct regulation branch and indirect control main path, four of them are considered as coherent feed-forward loops (CFFL), the other four structures are called incoherent feed-forward loops (IFFL). The effects of transcription factors are integrated in the promoter region of target gene. The expression of target gene is modulated on the basis of the concentration of transcription factors bound to their inducers. This modulation is described by the cis-regulatory input function, including AND-gate logic and OR-gate logic. In the past decades, more and more attention has been paid to the functions, structures, as well as noise characteristics of feed-forward loops.^[22,28–42] The regulation mechanisms of feed-forward loops in cell fate decisions in budding yeast were studied.^[20] It is found that the coherent feed-forward loop responds only to persistent stimuli and rejects transient input pulses as shown in Ref. [28]. The noise characteristics of the feed-forward loop in the steady state have been studied by using the Langevin formalism and numerical simulation.^[32] Furthermore, the principle of noise decomposition and the mechanism of noise transmission in a coherent feed-forward transcriptional regulatory loop has been studied in our recent work.^[43]

However, in our research above, only the kind of coherent feed-forward loop with OR-gate logic was considered, but the AND-gate logic was not taken into account. In addition, the incoherent feed-forward loops with AND-gate logic were not explored either. In order to obtain more general observations about the fluctuation decomposition and noise propagation in the feed-forward transcriptional regulatory loop, we will investigate the stochastic dynamic behaviors of these various types of feed-forward transcriptional regulatory loops. The rest of this paper is organized as follows. In Section 2, the mathematical models of twelve kinds of feed-forward loops are presented first. Then the relevant theoretical and simulation methods are introduced to calculate variances and normalized variations of all components for the twelve kinds of motifs. Theoretical expressions of noise propagation and decomposition are obtained. Furthermore, in Section 3, we analyze the fluctuations and noise propagations in the twelve kinds of feed-forward loops. Three important findings are summarized. The underlying biophysical mechanisms are also supplied. Finally, some conclusions are drawn from the present study and discussed in Section 4.

A feed-forward loop is composed of three components: two transcription factors X and Y, where the former regulates the latter, and a target gene Z, where X and Y both bind the regulatory region of Z and jointly modulate the transcription rate (Fig. 1). Below, X means the upstream factor, Y represents the intermediate component, and Z is the downstream element. Each of the three sides of the feed-forward loop is corresponding to activation or inhibition, so there are eight kinds of feed-forward loops.^[28] Four of them are called coherent feed-forward loops, that is, the direct regulation branch (from X to Z) and the indirect control main path (from X through Y to Z) play the same regulatory function. The other four structures are named incoherent feed-forward loops, i.e., the direct and indirect control paths are acting in reverse.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Twelve different types of feed-forward loops, including coherent feed-forward loops with AND-gate logic, coherent feed-forward loops with OR-gate logic, and incoherent feed-forward loops with AND-gate logic.

For coherent feed-forward loops, the efficacy of the transcription factors X and Y is integrated in the promoter region of target gene Z, thus the expression level of Z is regulated according to the transcriptional concentrations of X and Y bound to their inducers. This modulation is represented by the cis-regulatory input function.^[44–46] Cis-regulatory input functions contain (i) AND-gate logic, in which both X and Y are needed in order to express target gene Z, (ii) OR-gate logic, in which either X or Y is adequate to express downstream gene Z.

Therefore, the feed-forward loop consists of twelve different types as shown in Fig. 1, including coherent feed-forward loops with AND-gate logic (Figs. 1(C1a)–1(C4a)), coherent feed-forward loops with OR-gate logic (Figs. 1(C1o)–1(C4o)), and incoherent feed-forward loops with AND-gate logic (Figs. 1(I1a)–1(I4a)).

In order to study the general noise characteristics of twelve different types of feed-forward loops, the theoretical formulas of noise in various kinds of feed-forward loops are derived by using the linear noise approximation, numerical results by Gillespie simulation,^[47] and their results are compared with the analytic results.

2.1. Deterministic model and steady state

In accordance with the biochemical reaction rules,^[28] a set of ordinary differential equations is established for the mathematical modelling of relevant gene regulatory networks.^[28] The process of generation and annihilation of upstream factor X is considered, the feed-forward loop model has three variables. Take a kind of coherent feed-forward loop with AND-gate logic (Fig. 1(C1a)) for example, the kinetic process can be described by the following equations:

where variables x, y, and z are the concentrations of X, Y, and Z, respectively; α_x is the protein production rate for X, α_y, and α_z are the maximum levels of activated protein production for Y and Z, which are both set to be ten; the Hill coefficient n and the corresponding Hill constants K_xy, K_xz, K_yz are all set to be unity; δ_y and δ_z are the degradation and dilution rate of Y and Z, which are both set to be unity.

No matter what initial states the system starts from, it eventually tends to be a steady state, that is, the attractor of the system. The feed-forward loop has an attractor as the attracting fixed point

in Eqs. (1)–(3).

2.2. Stochastic model and analytical expression of noise

In the case of a small number of molecules, the random noise can be described accurately by the master equation. A theoretical deduction about the noise formula is given below, proceeding from the master equations. The numbers of the expression productions are expressed as N_i, . is defined as the size of system then the numbers of the expression productions of X, Y, and Z are correspondingly denoted as , , , where is set to be 100 throughout the paper. In order to characterize the noise, the linear noise approximation is used below.

In the case that the Hill coefficient n = 1, the Hill constants , the joint probability distribution of coupled ordinary differential equations Eqs. (1)–(3) conform to the following master equation:^[48,49]

where symbol E is defined as , , which represents a step operator. It is difficult to solve the master equation exactly, so a systematic approximation method has to be adopted here. The numbers of Y and Z are approximated by setting and by using van Kampen’s -expansion method. The joint probability distribution is described by . Collecting the terms of in the expansion of Eq. (4) reproduces the concentration form of the macroscopic rate equation and collecting the terms of gets a linear Fokker–Planck equation,where A is the stationary Jacobian matrix and B is the stationary diffusion matrix.

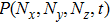
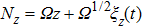
Consequently,

The linear noise approximation is summarized by^[50,51]

where matrix C contains the variances C_xx, C_yy, , which describes the fluctuations of X, Y, and Z. Substituting Eqs. (6) and (7) into Eq. (8), we obtain In order to quantify the noise propagation near the steady state, equation (8) is normalized aswith , , and .

To measure how the balance between production and elimination of N_i is affected by N_k,^[2,52–56] the logarithmic gain is defined as , where N_i and N_k indicate the numbers of the expression productions, i, , is the pure production rate and is the pure elimination rate of the expression production. H_ik is a common method of evaluating the sensitivity as a response to change in parameter N_k, also known as logarithmic gain, susceptibility,^[57] or sensitivity amplification.^[58] Considering the constant transition rate and death rate, we can obtain the logarithmic gains as follows:

Under the steady state (i.e., , the average lifetime τ_i is determined by the total rate of elimination. Accordingly, it can be obtained that , .

Therefore, the drift matrix A is rewritten as . Its normalized formation M is represented as

To obtain theoretical expressions of noise propagation, we substitute Eq. (13) into Eq. (14), and then solve Eq. (12) for the normalized variations V_xx, V_yy, and V_zz here, and we have From the accompanied signal transduction in the network, it is seen that the noise is also transmitted along these pathways. The upstream factor X has contributions to the total noise in the downstream element Z via one-step (branch road, i.e., ) and two-step (main road i.e., ) propagation, respectively. The intermediate component Y also delivers a part of noise to Z through one-step propagation (i.e., ). It is worth noting that the analytic expression of total noise in Z seems to be complex. However the third term on the right-hand side describes the two-step propagation noise from X to Z.

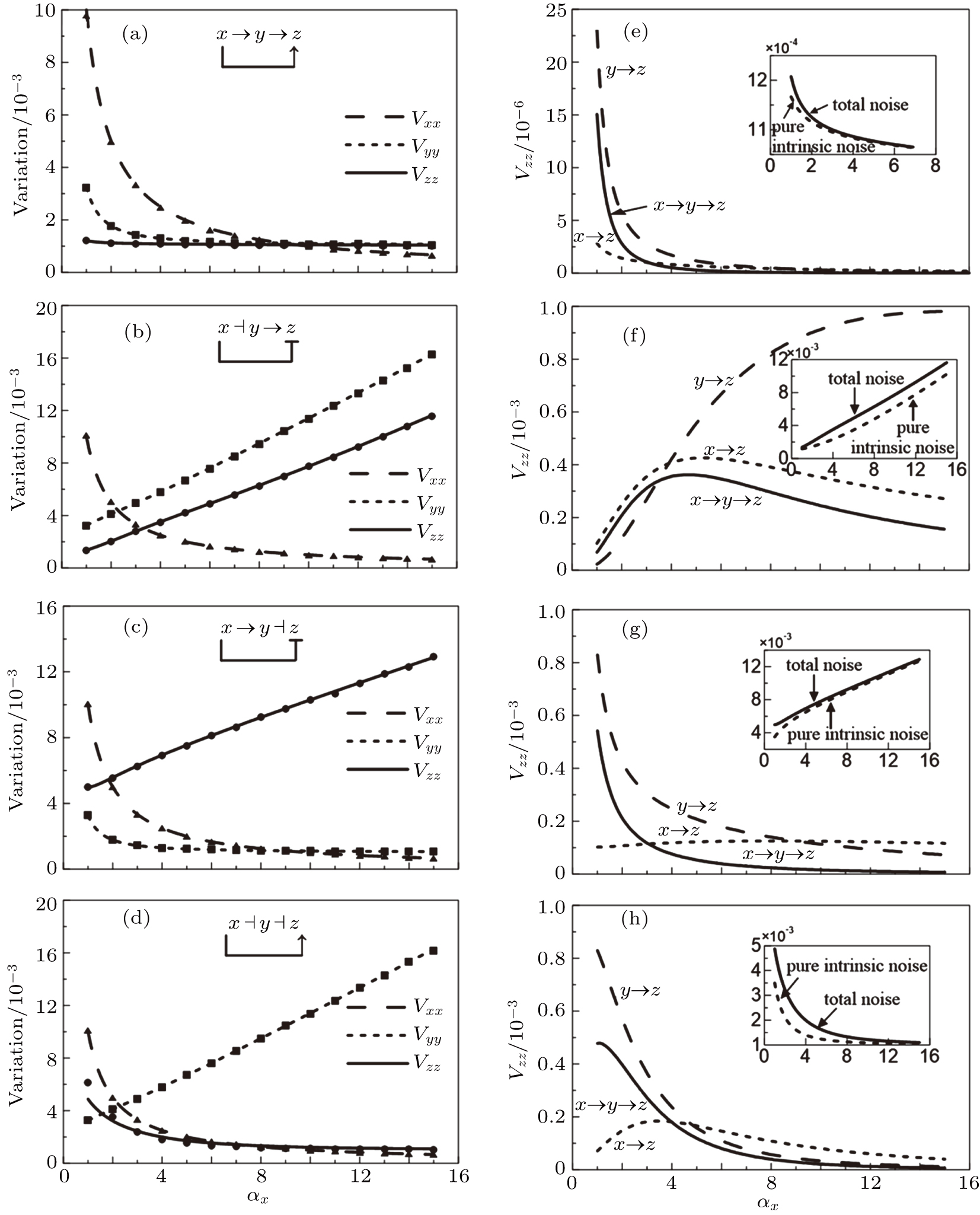
The method we proposed in the present article allows us to calculate the contributions of different components to the total variability of a system output. According to the theoretical formulas of the variance and the normalized variance obtained by the above calculations, we can make a more profound analysis about how the noise propagates in the feed-forward loop. Some interesting results for the twelve kinds of the feed-forward loops are found by the noise decomposition method (Fig. 1).

3.1. Noise propagation mechanism of incoherent feed-forward loops with AND-gate logic

In a biological system, incoherent feed-forward loops are also as common as coherent feed-forward loops. Hence we study noise characteristics of different nodes in these small gene networks as observed in Eqs. (15)–(18). The normalized variations of each element in a variety of situations are derived, which can present a global feature. Based on the theoretical formula of noise propagation obtained above, the total noise and noise decomposition of incoherent feed-forward loop with AND-gate logic are plotted in Figs. 2(a)–2(d) and 2(e)–2(h), respectively.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. ((a)–(d)) Normalized variations of different genes for four different types of incoherent feed-forward loops of AND-gates. Lines represent theoretical predictions, and solid markers refer to simulations using the Gillespie method. ((e)–(h)) Noise decompositions of downstream factor Z in four different types of incoherent feed-forward loops of AND-gates.

As illustrated in Figs. 2(b) and 2(d), the total noise of Y (i.e., monotonically increases with the increase of α_x in this kind of feed-forward loop. At the same time, the total noise of Z (i.e., exhibits an upward trend in the two types of feed-forward loops shown in Figs. 2(a)–2(b). In particular, in Fig. 2(d), the total noise of Z appears to have a minimum point of noise when α_x increases. When the biological system is at this minimum, the stochastic noise is minimal, which is most favorable for the propagation of signals.

As shown in Figs. 2(e)–2(h), an important characteristic is that the two-step propagation noise from X (i.e., ) is negative in the incoherent feed-forward loops. With the increase of α_x, the two-step propagation noise from X gradually increases, and finally approaches to zero. This may be that the total noise of X is large in the case of small concentration of X, and the noise of Z is suppressed and reduced through indirect transmission in the main road.

As demonstrated in Eq. (18), the noise component of two-step propagation consists of four terms. Combining this mathematical expression and Table 1 (see AND-gate logic in IFFL), it is found that each term has plus sign due to the operation for logarithmic gains in these terms. Therefore, the two-step propagation noise is negative.

Table 1.

	Figure Option ViewDownloadNew Window
	Table 1. H matrices corresponding to twelve different types of feed-forward loops.

This novel result indicates that the noise control function for downstream regulation not only is related to the positive or negative regulation property, but also is associated with the regulation step-number in the pathway. Even though the regulation sign is positive, mediated by intermediate factors, upstream factors can still implement the noise suppression control, hence indirectly reducing the randomness of downstream factors.

3.2. Noise propagation mechanism of coherent feed-forward loops with OR-gate logic

The noise characteristics and noise decomposition of coherent feed-forward loops with OR-gate logic have already been investigated in our recent work.^[43] Several other types of coherent feed-forward loops with OR-gate logic are further considered here. According to the theoretical Eqs. (15)–(18), we can derive the total noise and noise decomposition of coherent feed-forward loops with OR-gate logic, and the results are plotted in Figs. 3(a)–3(d) and 3(e)–3(h), respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) ((a)–(d)) Normalized variations of different genes for four different types of coherent feed-forward loops of OR-gates. Lines represent theoretical predictions, and solid markers refer to simulations using the Gillespie method. ((e)–(h)) Noise decompositions of downstream factor Z in four different types of coherent feed-forward loops of OR-gates.

As demonstrated in Fig. 3(b)–3(c), the total noise of Z monotonically increases with the increase of α_x in each of the two types of feed-forward loops when the control of branch is negative. At the same time, the total noise of Y shows an upward trend in each of the two types of feed-forward loops, see Figs. 3(b)–3(d).

As observed from the noise decomposition diagram of downstream factor Z, i.e., Figs. 3(e)–3(h), it is found that the total noise of Z mainly originates from its internal noise. Unlike the previous results, the one-step propagation noise from X (i.e., ) is nonmonotonic as plotted in Figs. 3(f)–3(h). With the increase of α_x, the one-step propagation noise from X changes from small to largest, then decreases, and there exists a strongest point. This result indicates a nonlinear behavior of random noise of coherent feed-forward loops with OR-gate logic. It means that the randomness of downstream factors can be optimized under the one-step propagation, reflecting the diversity and flexibility of noise control. In addition, from Fig. 3(f) it follows that the two-step propagation noise from X also first increases and then decreases.

From Eq. (17), the noise component of one-step propagation is just one term. Based on this mathematical expression of one-step propagation noise and Table 1 (see OR-gate logic in CFFL), it can be deduced that the noise term is exactly a nonmonotonic function of α_x. In addition, this nonmonotonic curve also originates from a competition mechanism of molecular number. On one hand, with α_x increasing, the average number of X is enhanced. On the other hand, the molecular number joining the reaction in the branch is reduced largely and then is raised. Therefore, a maximum value is observed for one-step propagation noise from X to Z.

3.3. Noise propagation mechanism of coherent feed-forward loops with AND-gate logic

According to the theoretical Eqs. (15)–(18), the normalized variances for different kinds of coherent feed-forward loops with AND-gate logic are illustrated in Figs. 4(a)–4(d). It is found that total normalized noise levels of X is reduced with the increase of the production rate α_x of upstream factor, which is consistent with our recent study,^[43] but the total noise levels of Y and Z are different. For the two types of feed-forward loops shown in Figs. 4(b) and 4(d), the total noise levels of Y increases monotonically with α_x increasing.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. ((a)–(d)) Normalized variations of different genes for four different types of coherent feed-forward loops of AND-gates. Lines represent theoretical predictions, and solid markers refer to simulations using the Gillespie method. ((e)–(h)) Noise decompositions of downstream factor Z in four different types of coherent feed-forward loops of AND-gates.

Interestingly, the total noise level of Z exhibits a monotonic upward trend for the feed-forward loop when the regulation property of branch road is negative as exhibited in Figs. 4(b) and 4(c). Moreover, for the twelve kinds of feed-forward loops, the total noises of the downstream factor Z all increase monotonically if the regulation of the branch is negative. This result is consistent with the principle of concentration-driven-noise. As the concentration of upstream factor X increases, the concentration of downstream factor Z is suppressed because the branch road is negatively regulated. With the decrease of the molecule number in Z, the fluctuation V_zz becomes larger.

In order to further explore how the noise propagates in the feed-forward loop, the noise decomposition results of downstream factor Z are described in Figs. 4(e)–4(h). It is shown in Figs. 4(e)–4(h) that the total noise of Z mainly comes from internal noise, which is consistent with our recent research result,^[43] but the one-step and two-step propagation noises are different. It is found from Fig. 4(f) that the one-step propagation noise from Y increases with the increase of α_x, while the two-step propagation noise from X first increases and then decreases, exhibiting a non-monotonic property.

The transmission mechanisms of complex signals in biological systems have been investigated widely.^[59,60] It is well known that noise is unavoidable for these cellular systems.^[61–63] Therefore, more and more studies focused on the mechanism of noise propagation in a biochemical network.^[64,65] In this paper, the noise characteristics and propagation mechanisms of twelve kinds of feed-forward gene transcriptional regulatory loops are investigated. The theoretical formulas of total noise and noise decomposition are theoretically derived by using linear noise approximation. Our approach is widely applicable and does allow us to disentangle the different contributions to system output resulting from the different components in a system. Three general results of noise transmission in these feed-forward loops are found. (i) For incoherent feed-forward loops with AND-gate logic, the two-step noise propagation of upstream factor is negative. (ii) For coherent feed-forward loops with OR-gate logic, the one-step propagation noise of upstream factor is non-monotonic. (iii) For all feed-forward loops, if the branch road of the feed-forward loop is negatively controlled, the total noise of downstream factor monotonically increases. The potential mechanisms and biological relevances are presented.

Due to lack of experimental data, it is difficult to build a quantitative feed-forward loop model. Only a coarse model of feed-forward loop is used to explore the qualitative behaviors. In order to check the robustness of our observations, the theoretical results are further investigated in a much wider range of parameters.

First, for incoherent feed-forward loops with AND-gate logic, we study the two-step propagation noise in order to verify whether upstream factors can inhibit signal noise indirectly by reducing the randomness of downstream factors. As an example, a kind of incoherent feed-forward transcriptional regulatory network (Fig. 1(I2a)) is chosen. Figure 5 shows the numerical results for a ten-fold increase or decrease in certain parameters. The funnel-shaped curves are observed. In most of the cases, the change of parameter value only adjusts the position of valley in each of these noise curves. It should be pointed out that when we change α_z, the dependence of two-step propagation noise on α_x is unchanged. In particular, by our sensitivity analysis, it can be seen that the two-step propagation noises are still negative when adjusting these parameter values.

Fig. 5.

Figure Option ViewDownloadNew Window

Fig. 5. Two-step propagation noises for parametric variation of incoherent feed-forward loop of AND-gates. To change the parameters of the lower right corner of the figure, different graphics can be obtained. Solid lines indicates that , , , n = 1, the short dotted line represents a ten-fold reduction in parameters, the long dotted line represents a ten-fold increase in parameters. The short dotted line represents n = 2, solid line indicates n = 4, the long dotted line represents n = 6.

Second, for coherent feed-forward loops with OR-gate logic, it is found that the one-step propagation is non-monotonic. When the control parameter is at a moderate value, the noise intensity of downstream factor is magnified. In contrast, the further reduction or enlargement of control parameters, the randomness of the downstream factors can be optimized under the first-order propagation. In view of coherent feed-forward gene regulation network with OR-gate logic (Fig. 1(C2o)), the one-step propagation noise from X is investigated. The parameters are changed accordingly as shown in Fig. 6, and the numerical results for a ten-fold increase or decrease of certain parameters are plotted. The bell-shaped curves are observed. It can be seen that the non-monotonic property of one-step propagation noise remains unchanged when the parameter values are changed.

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. One-step propagation noises for parametric variation of coherent feed-forward loop of OR-gates. To change the parameters of the lower right corner of the figure, different graphics can be obtained. Solid line indicates that , , , n = 1, the short dotted line represents a ten-fold reduction in parameters, the long dotted line denotes a ten-fold increase in parameter. The short dotted line refers to n = 2, solid line indicates n = 4, the long dotted line refers to n = 6.

Third, for all kinds of feed-forward loops, as the concentration of upstream factor increases, the concentration of downstream factors will be suppressed if the regulatory branch is negatively regulated. According to the inverse relation of the square root of noise to molecular number, it is obvious that the noise of downstream factor is enhanced with upstream component increasing.

Fourth, it should be pointed out that the gap between the total noise and internal noise seems small in these results, however under different parameter values, it is noticed that the total noise may not be dominated by the internal noise. In particular, when the production rate and degradation rate of Z are adjusted, the propagation noise becomes large, close to the internal noise.

It should be pointed out that we discuss the noise propagation varying only the expression level of the upstream factor α_x. However, the effect of other factors can be studied in a similar way. In particular, we can give some qualitative predictions if δ_x and α_x are fixed while another reaction rate is selected as the control parameter. (i) When treating α_y as the parameter, for incoherent feed-forward loop of AND-gates, the steady state value of X is a constant and the normalized variation V_xx is unchanged. Moreover, based on Table 1 (see AND-gate logic in IFFL), it can be deduced that the propagation weight in the noise term of one-step propagation noise in Eq. (17) is also unchanged. Hence the one-step propagation noise does not vary with the change of α_y. (ii) When regarding α_z as the parameter, the steady state values of X and Y are constant. From Eqs. (15) and (16), the normalized variations and V_yy are also fixed values. As observed from the expressions of propagation weight in one-step and two-step, we find that the noise components transmitted from X to Z directly and indirectly are both independent on α_z. Therefore, the adjustment of different reaction rates has different roles in noise transmission. However, as a typical stimulus-response system, we put our emphasis on the production rate α_x of upstream factor in the feed-forward loop in our work. Hence, the production rate α_x is considered as a stimulus on feed-forward loop which can be controlled experimentally.

The noise decomposition algorithm allows us to investigate in detail how the noise propagates through a reaction system and affects the cellular process. What can a biologist learn from our results in gene circuit design? A simple discussion for the biological meaning of the noise propagation in feed-forward loop is provided below.

The structure of the control network determines the function and dynamics of the network. While the topological properties of the control network are always unknown, it is necessary to predict the network structure from the dynamical behaviors of biological network. An especially interesting topic is how to deduce the corresponding network from the underlying stochastic dynamics. For example, the authors have shown that for a genetic system with a single transcription factor (an activator can act as an inhibitor when bound to sites downstream of the TATA box), the precise amount by which noise changes with expression is specific to the regulatory mechanism of transcription and translation that acts on each gene.^[66] Moreover, for feed-forward loops with two transcription factors, the previous theoretical and experimental research also has shown that the different feed-forward loops exhibit different relationships between mean expression and noise.^[67] Our work provides a systematic study about how the noise is distributed and controlled in the feed-forward gene transcriptional regulatory loops. The theoretical method of noise propagation through these three-node, feed-forward loops may allow researchers to understand the role of noise on cellular signal transduction in more complex biological networks. If we can design genetic circuits and measure these noise components, perhaps the network structure can be inferred with higher precision.

We believe that these results will motivate the further investigation on the transmission of biological noise and potential function on evolution. Obviously, it is a challenge to verify these theoretical observations with the real biological systems or experiments. However, with the development of yeast genetics, time-lapse fluorescent microscopy, single cell assays, and microfluidic devices, it is possible to trace the dynamics of key proteins in some simple synthetic gene circuits. Therefore, the stochastic noise and propagation mechanism could be tested by this single cell technology.