† Corresponding author. E-mail:
Stochastic characterization of radiation interaction is of importance to cell damage. Microdosimetry is to investigate the random structures of particle tracks in order to understand the dose-effect in cellular scales. In the review, we introduced the basic concepts of microdosimetry as well as the experimental methods (TEPC) and Monte Carlo simulations. Three basic biophysical models are interpreted and compared, including the target model, linear-quadratic model, and microdosimetric-kinetic model. The bottlenecks in the current microdosimetry research are also discussed, which need the interdisciplinary contributions from biology, physics, mathematics, computer science and electric engineering.
The ionizing radiation is a double-edged sword that has brought damage as well as benefits to human beings since the x-ray was discovered by Roentgen in 1895. The radiation therapy can kill primary tumors but may lead to the risks of secondary cancers several years after treatments.[1] The heavy ions of galactic cosmic rays may cause health risks to flight attendants and astronauts.[2,3] The cohort study for workers in nuclear industry illustrated the evidence of health risks, such as leukemia, lung cancers, cardio-cerebrovascular diseases and other non-cancer diseases.[4,5] The current system of radiation protection is based on the publications of International Commission on Radiological Protection (ICRP),[6] and the No. 60 publication is adopted in GB18871-2002, which is the basic standards of China for protections against ionizing radiation and for safety of radiation sources.[7,8] By reviewing available data relevant to cancer risks of the workers and the public from exposures to low levels of irradiation, ICRP concluded that the evidence supports the assumption of linear-no-threshold (LNT), where the cancer risk of irradiation is linearly dependent on the low dose without thresholds.[9] According to the LNT risk model, even the smallest doses have abilities to initiate cancer risks to humans.
The research on health risks associated with low levels of radiation exposures has several challenges. The first is that epidemiological investigations on low-level exposures require a large population and long-time follow-up visits.[2–5] The traditional low-dose studies are based on the estimations from high-dose cohorts of bomb survivors or nuclear accident survivors.[10–12] The extrapolation from cancer risks of high doses to low doses requires two assumptions.[9] One is the linear-no-threshold risk model. Another is that the risk units are individual targeted cells without effects from multi-cellular tissue levels. The second challenge is that the stochastic characterization of radiation interaction becomes substantial at low-dose levels, and the uncertainties are nontrivial for radiation effects on individual cells.[13,14] When the radiation ray interacts with a medium, it deposits energy in the path with discrete events. The spatial and magnitude distributions of energy deposition are non-uniform, and the track structures of energy deposition influence biological effects of irradiation. The third challenge is the tissue cell responses to radiation exposures, where non-targeted cells may be affected by targeted neighbors (bystander effects),[15] and the dose-effect may differ by time and by space.[9] Therefore, the investigations on dose-effects of low-level irradiation require contributions from different fields including biology, chemistry, physics, mathematics and computer science.
The subject matter of microdosimetry is to understand radiation biology through energy fluctuations in radiosensitive sub-regions of cells.[13,16] Microdosimetry was founded by Rossi around the 1960s,[16,17] and the concepts of probability distributions were originally introduced to describe random variables. To measure the energy distributions of micro regions, Rossi and his colleagues developed the theory of ionization pulse methods for the tissue-equivalent proportional counter (TEPC).[13,16] Keller proceeded to develop the theory and apply it in radiobiology.[14] In radiation protection and radiation therapy, the absorbed dose defined in macrodosimetry is the statistical average disregarding fluctuations, under which the energy depositions in micro domains may differ by several orders of magnitudes.[13,16] The deviations of microdosimetry from macrodosimetry are important for small volumes, low doses, or heavy-ion radiations. In addition, the clinical biological effectiveness (RBE) is frequently characterized by linear energy transfer (LET or L), which is also the statistical average of energy depositions per unit length in charged particle trajectories. Given the stochastic characterization, the RBE in subcellular volumes can no longer be quantified by LET, and the probability distribution of linear energy in microdosimetry is recommended.[14] Therefore, microdosimetry is the combination of biology and physics. Experimentally, it provides the techniques to measure the distribution of energy packages (doses) in micro regions.[13] Theoretically, it provides biophysical models to understand the dose-effects of radiobiology.[18–23] In this review, the concepts, simulations and measurements of microdosimetry are introduced, and three of the basic biophysical models on radiobiology are discussed.
In microdosimetry, the specific region is regulated as a spherical site of a diameter d, and the energy imparted is described by the term of specific energy z.[13,14,23] The specific energy z is defined as the imparted energy ε in the specific region per mass 

 |
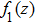


Microdosimetry quantities can be measured by the tissue-equivalent proportional counter (TEPC) (see TEPC section),[14] which facilitates the application of biophysical models to radiobiological experiments. However, if the subcellular structures like DNA are smaller than the TEPC measuring limit of 100 nm, Monte Carlo (MC) simulations are the alternative to provide the information of energy distributions in nano scales. The common MC simulation codes include MCNP, GEANT4, PHITS, and FLUKA.[25–31] In the MC simulation for macrodosimetry like MCNP, the details of particle interactions in nanometer scales are disregarded, and a large number of collisions are grouped to several steps. Comparing to other MC codes, GEANT4 developed the special package (G4DNA) to simulate particle tracks in nanometers.[26,28] The track structure codes from the ab initio physical mechanism provide adequate biological molecular information for radiation damage at cellular levels. Previous work found that the low-energy electrons (less than 1 keV) have high relative biological effectiveness (RBE), which produce approximately 50% ionization in the nano scale. However, the simulations of low-energy electrons consume extremely long computer time since atomic reactions are nearly elastic with little energy dissipation. Furthermore, the physical models of those track structure codes depend on the data of reaction cross sections, and the experimental data are available until the electron energy is less than 250 eV. Therefore, the theoretical estimation of cross-sections and the cutoff for low-energy electrons bring deviations to microdosimetry simulations, although the track structure codes provide significant impacts on the process of radiation protection.
The target-hit model has been widely used in radiobiology to understand the dose-effect relation of cell survival fractions and to quantify the radio-sensitiveness of cells.[13,14,23] In this model, the cell becomes inactive if its radiosensitive subcellular units (termed “targets”) are hit. The curve of cell survival fraction versus dose is determined by two factors: one is the minimal hit targets to inactivate a cell, and another is the minimal hits to inactivate a target. For the simplest case (one target & one hit), a cell contains one target, and it can be killed once the target is hit. Given the stochastic characterization of irradiation interaction with cells, the inactive cells follow the Poisson distribution in cell population. Given the cell survival fraction S after irradiation, the change of S as a function of the lag time 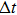
 |


 |
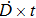



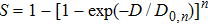

 |


In the linear–quadratic (LQ) model, the principle target for the radiation effect on a cell is deoxyribonucleic acid (DNA) with the structure of double strands held together by base pairs.[13,16,23,32] The cell lesion owing to the single strand breaks (SSBs) is repairable, given that the damaged sites can be repaired using the opposite strands as a template. By the contrast, if the breaks happen in two strands and the damaged sites are just opposite one another or a few bases apart, it leads to the double strand break (DSB), which is the most important lethal lesion resulting in cell killing. One DSB may be triggered by one single hit of energy deposition or the combination of two hits. The DSB probability of the one-hit event is linearly dependent on the irradiation dose D, and the two-hit combination is dependent on the dose square 
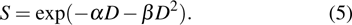 |


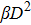

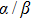

The LQ model can be derived from the theory of microdosimetry.[16,23] The function of macro dose-effect η can be quantified by
 |


 |

 |

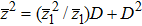
 |
The microdosimetric-kinetic (MK) model is developed by Hawkins,[19–22] which examined the relations between RBE and LET in radiobiological experiments. By regarding the subcellular structures as spherical domains, it considers the DNA repairing inside and between those domains. The model assumes two types of DNA lesions after irradiation.[19–22] Type I is unrepairable lesion produced by single track of ionizing radiation (one hit). The average number of lethal lesions per domain for the type-I lesion is 

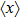
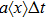
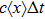
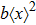
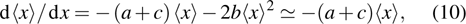 |

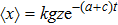
 |

 |

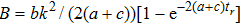
 |

MK model found that the linear relationship between RBE and LET maintained at the low dose level for low LET, but for high LET the linear dependence failed due to the departure of cell lesions from Poisson distribution, which is important for radiation protection on heavy ions and cosmic rays.
Microdosimetry theory provides an equivalent experimental model to evaluate energy distributions in sensitive subunits of cells since the direct measurements are impossible. According to Fano theorem, the density of the medium with certain component proportions does not change the distributions of particle fluencies and energy depositions in an isotropic irradiation field.[14,23,34] Thus, the equivalent gas in microdosimetry can represent the solid of the same element components, which have the same energy deposition per unit mass (absorbed doses). Assuming the particle fluency follows Poisson distributions, the relative fluctuations in the equivalent gas (R) to the solid (r) is
 |


Tissue-equivalent proportional counter (TEPC) is the microdosimetric detector based on this theory, where the centimeter-size probe of a proportional counter detects the energy fluctuations of the tissue-equivalent gas.[14,23,34] The pulse spectra from the signal of the proportional counter is as follows:
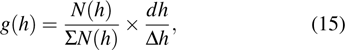 |


 |

The statistic characterization of energy depositions of irradiation is from the stochastic interactions of irradiation with medium, and the macrodosimetry disregards the fluctuations by statistical averages. For the situations of small volumes, low doses, or heavy-ion radiations, the fluctuation deviations from the averages are important for the radiation protection and radiation therapy. Microdosimetry is aimed to quantify energy depositions in micro regions, where energy fluctuations lead to large deviations from the absorbed doses in macro scales. The application of microdosimetry theories on biophysical models provides the insights on the radiation effects in radiobiology. The target model is the early approach to consider the stochastic nature of energy depositions in radiobiology, which is simple to apply on the experimental fitting of cellular survival curves. LQ model considers both lethal lesions and sublethal lesions for cell damage. The ratio of linear parameter α and quadratic parameter β is critical for the clinic estimation of biologically effective dose (BED) in radiotherapy. LQ model also has the background of microdosimetry theory, where the fluctuations of specific energy z as well as the interaction matter result in the parameters of the linear and quadratic terms. Microdosimetric kinetic model proceeds to develop the linear-quadratic formula, which includes the dynamics of DNA damage and repairs, such as diffusing lesions (domains) on the strands, DSB transformation and lesion persisting time. With the combination of MC simulations and biophysical models, microdosimetry can provide substantial details on energy distribution in subcellular structures. However, the purpose of microdosimetry is to find essential parameters to understand radiobiology from the complicated structures of particle tracks, and more work is needed for the connection between physical characteristics of track structures and the radiobiological effects on subcellular levels.
There are several challenges in the process of microdosimetry. The first is that the size resolution of TEPC measurement is down to the limit of 100 nm, which prohibits the developments from the micro scale of cells to the nano scale of DNAs. The second is the experimental data of the reaction cross sections are unavailable for low-energy electrons (less than 250 eV), which leads to the deviations of different MC code simulations on low doses. The low-energy electrons usually have high RBE and thus are important to the DNA damage in the nano scale. The third is that imaging resolutions for the sensitive marks of biological damage are limited by the microscopic techniques. DSBs can be identified through the fluorescent images of γ-H2Xs foci, but it is hard to separate the individual sites from the clusters of bright spots in the microscopic imaging. The fourth is that the computer time of MC simulations is extremely extended for low-energy electrons, and current strategies of computer algorithms are to set cutoff values for low-energy limit. Therefore, microdosimetry is the interdisciplinary area, whose improvement needs continuous support from other fields, such as biology, physics, mathematics, computer science and electric engineering.
We thank Yang H, Pei H and Zhou G for helpful discussions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |

