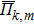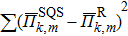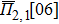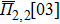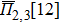† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11647010 and 11704020), the Higher Education and High-quality and World-class Universities (Grant No. PY201611), and the Fund for Disciplines Construction from Beijing University of Chemical Technology (Grant No. XK1702).
The electronic structure and thermoelectric (TE) properties of PbSxTe1−x(x = 0.25, 0.5, and 0.75) solid solution have been studied by combining the first-principles calculations and semi-classical Boltzmann theory. The special quasirandom structure (SQS) method is used to model the solid solutions of PbSxTe1−x, which can produce reasonable electronic structures with respect to experimental results. The maximum ɀT value can reach 1.67 for p-type PbS0.75Te0.25 and 1.30 for PbS0.5Te0.5 at 800 K, respectively. The performance of p-type PbSxTe1−x is superior to the n-type ones, mainly attributed to the higher effective mass of the carriers. The ɀT values for PbSxTe1−x solid solutions are higher than that of pure PbTe and PbS, in which the combination of low thermal conductivity and high power factor play important roles.
Thermoelectric (TE) materials have attracted much research interest in recent decades due to their widespread application prospects for waste heat recovery. The performance of a specific TE material is evaluated by a dimensionless figure-of-merit, ɀT = σS 2T/(κ l + κ e), where S is the Seebeck coefficient, σ is electrical conductivity, T is the absolute temperature, and κe and κl are electronic and lattice thermal conductivities, respectively. For an excellent TE material with high conversion efficiency, it should combine simultaneously high values of power factor (PF), S 2σ, and low thermal conductivity. Many methods have been proposed and implemented to improve the ɀT values, such as formulating new structures,[1] the fabrication of superlattices or quantum dots,[2–4] doping foreign elements,[5–8] and the formation of solid solution alloying.[9,10]
PbX (X = Te and S) is one of the best materials for thermoelectric generators intended for operation at middle temperatures (from 400 K to 800 K). The high band degeneracy in the PbX materials is favorable for a high Seebeck coefficient.[11,12] Meanwhile, the strong anharmonic coupling between LA and TO phonon modes indicates that the lattice thermal conductivity can be reduced to a very low level.[13,14] Most studies have been performed to clarify or improve the performance of PbX.[15–21] For example, Dmitriev et al.[15] studied the PbTe using three-band model method and found a peak ɀT value of 0.7 and 0.6 for p-type and n-type at 700 K, respectively. Wang et al.[16] have then successfully synthesized n-type PbS with ɀT value of 0.7 at 850 K. Jin et al.[17] proposed a simple hydrothermal route for the synthesis of PbS–PbTe core-shell heterostructured nanorods, which produce the maximum PF of 294 μW/mK2. Ibanez et al.[18] investigated the n-type (PbTe)1−x(PbS)x nanocomposites and obtained the ɀT value of ~ 1.1 at 710 K. Korkosz et al.[19] studied the solid solution p-type (PbTe)0.88(PbS)0.12 and found that the phonon scattering from solid solution defects can reduce the thermal conductivity, which leads to a high ɀT value of 1.6 at 800 K. It is revealed that the solid solution is an effective way to improve TE performance, since it tends to cause the distortion of electronic bands[22] and introduce the nano-precipitates.[23]
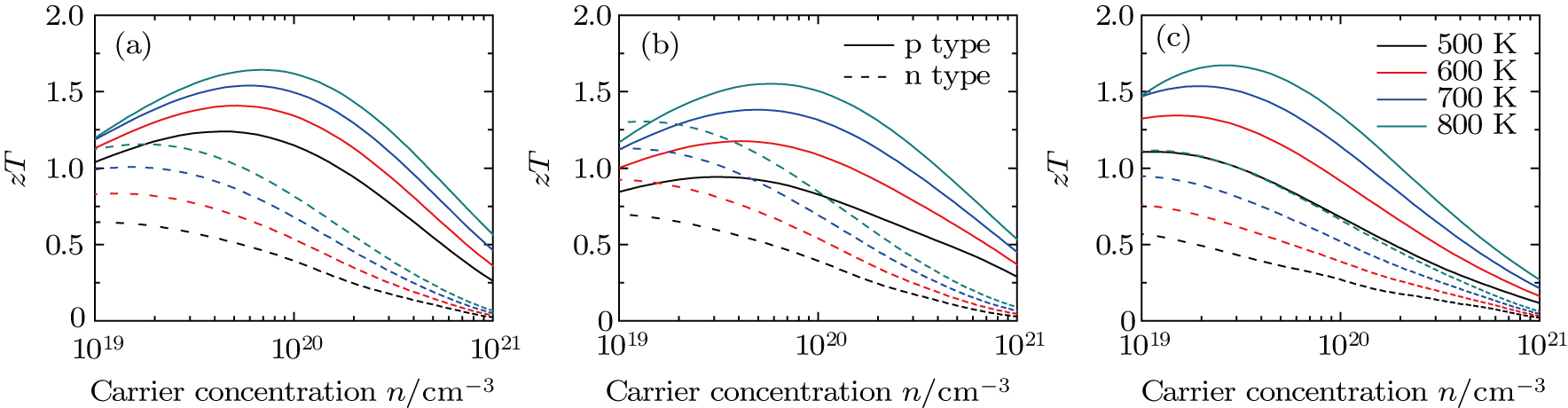
In this study, we investigate the TE properties of n-type and p-type PbSxTe1−x solid solutions based on the first-principles calculations and special quasi-random structure (SQS) method.[24] The SQS method has been successfully combined with first principles to study the electronic and thermodynamic properties of disordered phases,[25–27] the basic idea of which is to produce an SQS with configurational correlation functions (CF) very close to those of solid solutions. Balancing the limitation of computer capability and calculation accuracy, we take the maximum usage of SQS-32 cell to model the disorder phase. The maximum ɀT value of 1.67 is obtained for p-type PbS0.75Te0.25 with a carrier concentration of 2.57 × 1019 cm−3 at 800 K, while the maximum ɀT value of n-type is 1.30 for PbS0.5Te0.5 with a carrier concentration of 1.34×1019 cm−3. We believe that these valves provide reliable reference for PbSxTe1−x solid solutions since the SQS structures are very close to the real disorder state. In comparison with pure PbTe and PbS, it also provides some understanding of the effects of Te/S ratio upon electronic and TE properties.
In the SQS method,[24] the pseudo-spin, Si = ±1, is introduced to assign the atom sites of the configuration occupied by A or B atom. The configurational correlation function, f(k, m), is defined to group these lattice sites. The f(k, m) have k vertices, where k = 1, 2, 3,… responds to point, pair, and triplet, …, respectively, and span a maximum distance of m, where m = 1, 2, 3, …, is the first, second, and third nearest neighbors, etc. These correlation functions are the average product of the spin variables over all sites of a figure. The aim of the method is to find the optimum SQS with correlation functions best satisfying the condition,
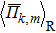
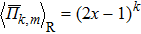
The PbSxTe1−x (x = 0.25, 0.5, and 0.75) solid solution structures are produced using the ATAT package,[28] and the corresponding electronic structures are calculated by density functional theory (DFT) as implemented in the Vienna ab initio Simulation Package (VASP).[29] The electron–ion interaction is described by the projector-augmented-wave (PAW) method.[30] The generalized-gradient approximation (GGA) with Perdew, Burke, and Ernzerhof (PBE) form[31] is used to describe the exchange–correlation function. The plane-wave cutoff energy is 500 eV, and the energy convergence criterion is chosen to be 10−5 eV. The integration over the Brillouin Zone (BZ) is done with 5 × 5 × 5 Monkhorst–Pack grid meshes[32] for all the SQS-32 structures to ensure the Hellmann–Feynman forces on each ion to be less than 0.02 eV⋅Å−1. The thermoelectric transport properties are calculated through the semi-classical Boltzmann theory and the rigid-band approach as implemented in the Boltz-Trap code,[33] where the constant scattering time approximation (CSTA) is used. The CSTA method does not involve any assumption about the possible strong doping and temperature dependence of relaxation time, τ, which has been successfully applied in predicting electrical transport properties for many TE material.[34–36] In this way, the Seebeck coefficient, S, is independent of τ, while the electrical conductivity, σ, and electronic thermal conductivity, κe, can only be evaluated with respect to the parameter τ.
The special quasi-random structures containing 32 atoms in the unit cell have been produced for three fractions, x = 0.25, 0.5, and 0.75, as shown in Fig. 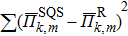
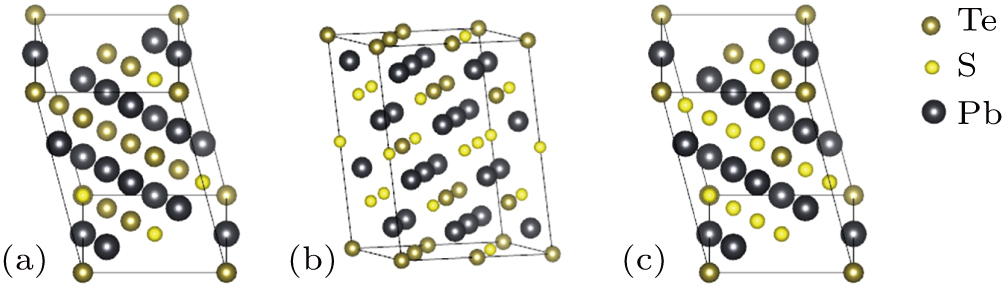 | Fig. 1. (color online) The special quasi-random structures of PbSxTe1−x solid solution with (a) x = 0.25, (b) x = 0.5, and (c) x = 0.75, respectively. The number of atoms in the SQS unit cell is 32. |
| Table 1.
Pair and multi-site correlation functions of SQS-32 structures. The number in the square bracket next to |
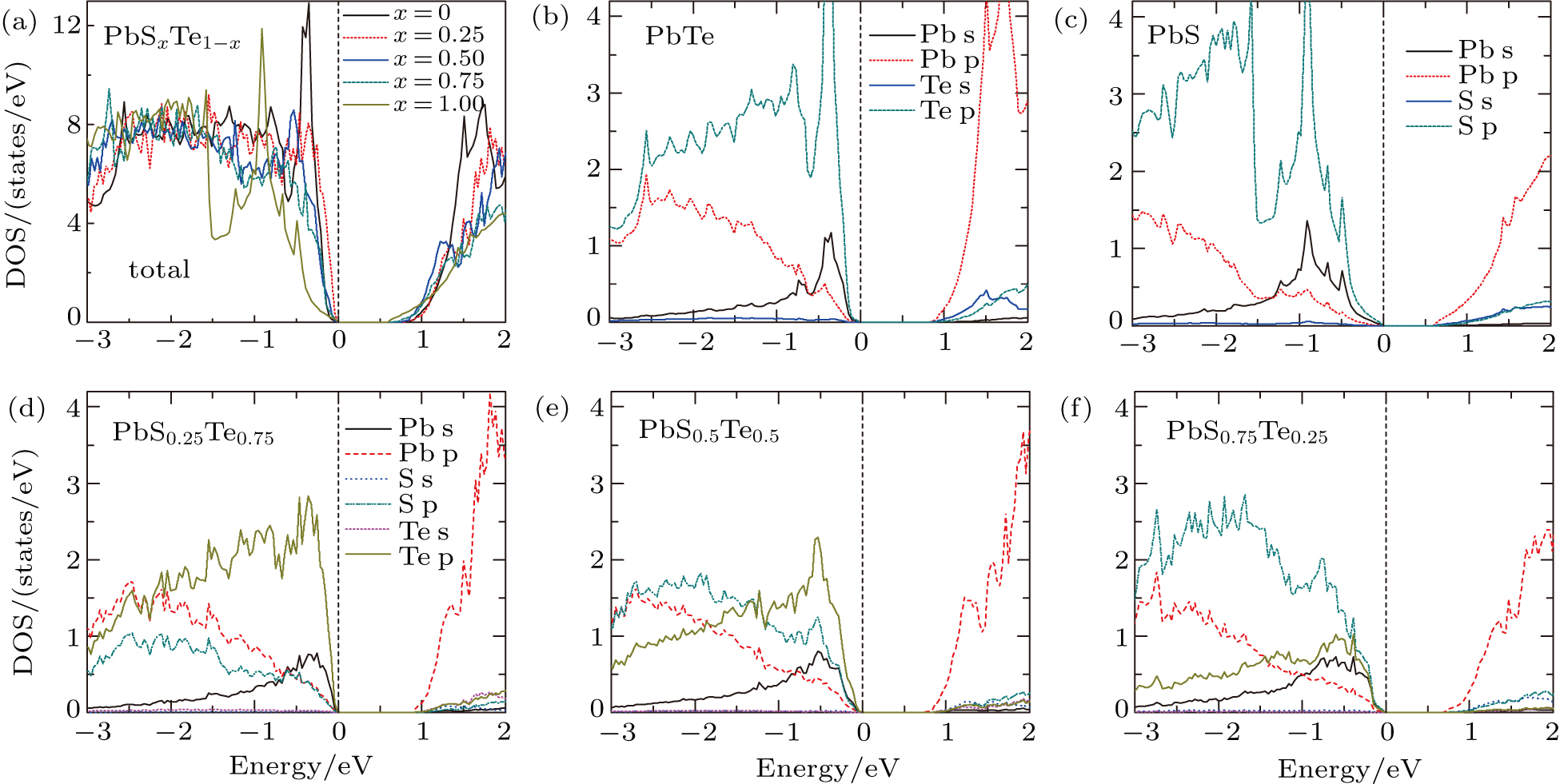
The total density of states (DOS) and projected DOS of PbSxTe1−x solid solution are shown in Fig.
For metals or degenerate semiconductors with parabolic band, the S is defined as[47]
Through the electronic structure, we can directly get the σ/τ ratio as a function of carrier concentration and temperature. The electrical conductivity, σ, can then be calculated by σ = (σ/τ) × τ. It is known that the τ is proportional to 1/T and n
−1/3 as a typical electron–phonon regime. The experimental data is used to simulate the behavior of τ. For p-type PbSxTe1−x, we use the data from Korkosz et al.,[19] in which the (PbTe)0.88(PbS)0.12 solid solution was synthesized. In this reference, the Seebeck coefficient is reported to be about 125 μV/K at 400 K. By comparing with the calculated values of S, we obtain the carrier concentration of n = 2.42 × 1020 cm−3. Using the experimental electrical conductivity of 1.00 × 105 S/m, we obtain a relaxation time of τ = 3.86 × 10−5T
−1n
−1/3. For n-type, we use the same method and choose the data from Ibánez et al.[18] at 710 K. Similarly, we obtain the τ=2.31 × 10−5T
−1n
−1/3. Then the electrical conductivities for PbSxTe1−x solid solutions can be obtained according to σ=(σ/τ) × τ, which are shown in Figs.
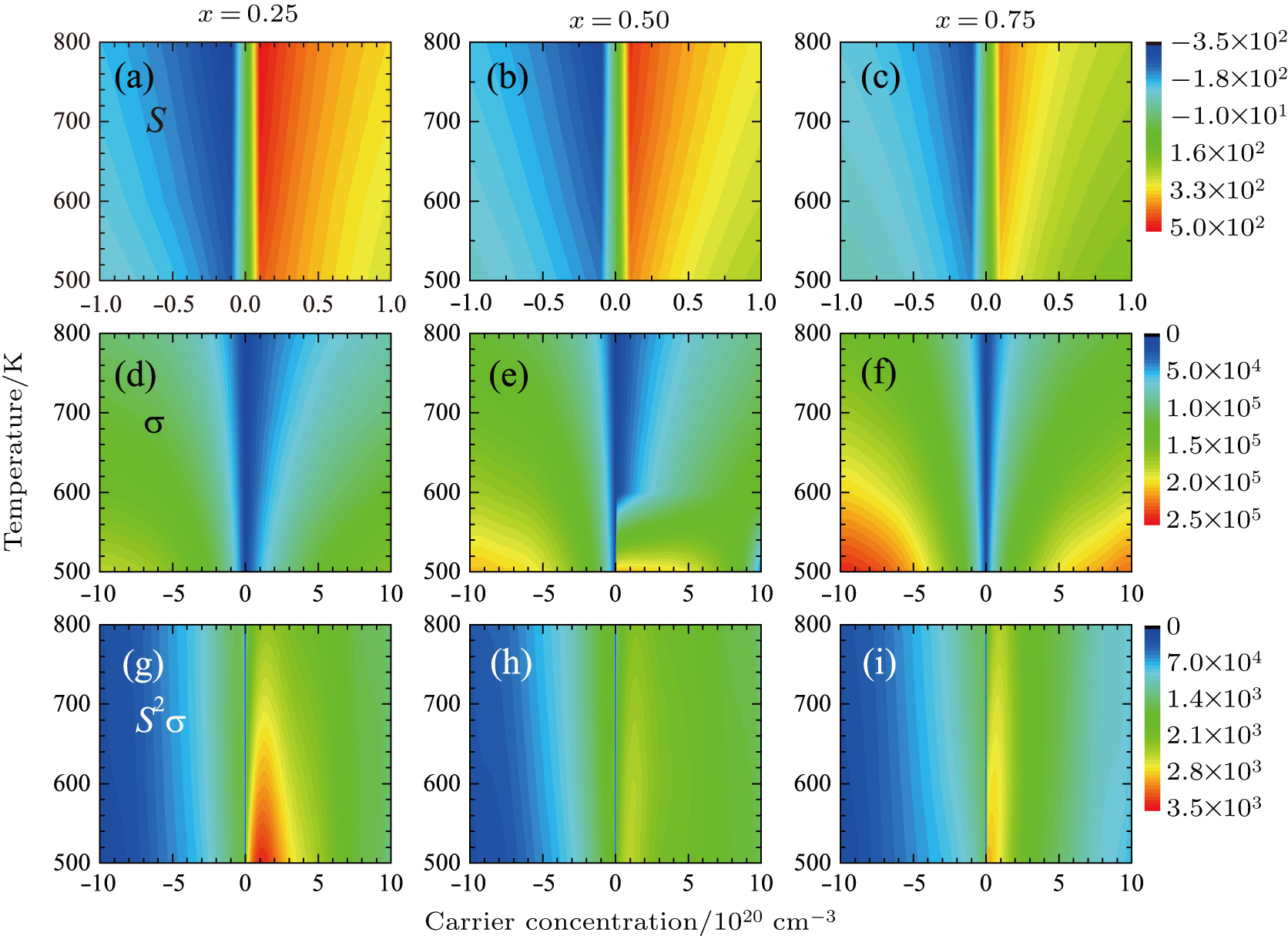
The power factor (PF), S2σ, can be easily obtained from the product of Seebeck coefficient and electrical conductivity, which are shown in Figs.
The electronic thermal conductivity, κe, was estimated according to the Wiedemann–Franz relation, κe = LσT, where L = 1.8 × 10−8 W⋅Ω/K2 is the standard Lorenz number. As shown in Fig.
The ɀT values of PbSxTe1−x can be calculated by the relations of ɀT = σS
2T/(κ
l + κ
e). The experimentally determined lattice thermal conductivity of PbS0.12Te0.88
[19] is used in the present calculations. According to the experimental results, as temperature increases from 500 K to 800 K, κl decreases from ~ 1.0 W⋅m−1⋅K−1 to ~ 0.75 W⋅m−1⋅K−1 following the typical 1/T scaling. In Fig.
In summary, the electronic structure and thermoelectric properties of PbSxTe1−x solid solution (x = 0.25, 0.5, and 0.75) have been systematically studied by combining the first-principles calculations and semi-classical Boltzmann theory. The special quasi-random structure method is used to produce SQS-32 unit cell to model the PbSxTe1−x solid solution, where the configurational correlation functions match well with those of random phases. The band gap shows a tendency of decline with increasing fraction x. The effective mass of carriers for p-type PbSxTe1−x is larger than that of n-type, leading to a higher Seebeck coefficient for p-type. At a typical temperature of 800 K, the ɀT reaches the maximum value of 1.67 for p-type PbS0.75Te0.25 with a carrier concentration of 2.57 × 1019 cm−3, while the maximum ɀT value of n-type is 1.30 for PbS0.5Te0.5 with a carrier concentration of 1.34 × 1019 cm−3. In general, the performance of p-type PbSxTe1−x is better than the n-type one. Compared to the pure PbTe or PbS, the thermoelectric performances of PbSxTe1−x solid solution are enhanced to a great extent.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |