† Corresponding author. E-mail:
We focus on molecular dynamics simulated two-dimensional complex plasma crystals. We use rigid walls as a confinement force and produce square and rectangular crystals. We report various types of two-row crystals. The narrow and long crystals are likely to be used as wigglers; therefore, we simulate such crystals. Also, we analyze the electric fields of simulated crystals. A bit change in lattice parameters can change the internal structures of crystals and their electric fields notably. These parameters are the number of grains, grains charge, length, and width of the crystal. With the help of electric fields, we show the details of crystal structures.
Suspended macroscopic grains in plasma environment make it complex. The grains acquire a large quantity of negative charge and can form crystal inside a plasma. In laboratories, a lower electrode prevents grains from falling. Negative grains repel each other to infinity unless a confinement force makes them close together. In a typical experiment, a negative electrode plays the confinement force role.[1–4] Also, uniform grains with equal mass and spherical shape are very common.[5–9]
Conditions for crystallization is given by Coulomb coupling parameter:[10–13]
 |
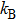
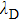
In most papers, spring force is used as confinement force:[19–23]
 |


Mirzanejhad and Bahadory[28] suggested an application for complex plasma crystals: they considered it as an electrostatic wiggler for free-electron laser, FEL. The FEL needs a long and strong transverse electric field. So, long complex plasma crystals with strong transverse electric field are better than a normal one for this purpose. In the present work, square, rectangle, and two-row crystals are simulated. These types of crystals can be long, and the transverse electric field of two-row crystals can be strong. We analyze the electric fields of these crystals and show that the electric fields of similar crystals differ a lot. Usually, crystals in laboratories are not complete and even small changes in grain positions leads to significant effects on the electric field in them. We discuss the effects of distance between rigid walls in two directions, grain number, and charge of each grain on the lattice type and number of rows in the crystals.
It must be noted that grain charge depends on the plasma parameters. For example, if plasma density or plasma temperature changes, grain charge will change. Sometimes, we use a normal quantity of grain charge and then we switch to another normal charge for comparison. We do not discuss experimental setup nor parameters that lead to a certain charge.
In a complex plasma, each charged particle has a screened Coulomb potential:[29–33]
 |
 |

Grains repel each other due to the force described in Eq. (
We use a molecular dynamics simulation. One of our purposes is to produce the crystals with arbitrary geometries and various sizes. In our simulations, grain charge, distance, and mass are normalized to electrons charge, Debye length, and grain mass respectively.
Figure
 | Fig. 1. Two square crystals. (a) n = 16, 





|
By selecting different values of length a and width b, square crystals become rectangular. Figure
By increasing rectangle length and reducing its width, the number of grain rows decreases. With the help of simulation, we can predict suitable distances for obtaining particular cases, such as three-row grains in crystal. Factors that affect the number of rows are n, q, a, and b. By increasing n and q, the number of grain rows increases. For constant a, by increasing b the number of rows increases and conversely for constant b, by reducing a the number of rows increases. A rectangular crystal that has just two rows of grains is a two-row crystal. The two-row crystals are part of a hexagonal lattice and in ideal conditions, each grain is located in the middle of two grains in the top row and bottom row. We simulate two-row crystals by a different method from the method reported previously.[24] Rigid walls assumption that is used in the present work is simpler and surprisingly gives more complete crystals than by the previous method.
Figure 



Except the length, figures
We are interested in long and narrow two-row crystals because they are suitable for FELs.[25] Narrow two-row crystals have strong transverse electric field that is essential for an electrostatic wiggler in FEL. On the other side, narrowing is equivalent to a small quantity of b, and small b leads to crystals with only one row. Our simulations are useful for predicting suitable conditions for the experimental setup. One of the long and narrow crystals is shown in Fig. 


In an ideal crystal, the frequency of longitudinal electric field Ex is twice the frequency of transverse electric field Ey; also the number of Ey peaks is equal to the number of grains in the crystal. The electric fields of crystals like those in Fig.
 | Fig. 5. (a) Longitudinal and (b) transverse electric fields in the middle of the crystal shown in Fig. |
The electric field components Ex and Ey of the crystals shown in Figs.
 | Fig. 6. (a) Longitudinal and (b) transverse electric fields in the middle of the crystal shown in Fig. |
Another thing is that grains have small oscillations, and so, all fields are momentary. We cannot produce 100% perfect crystals.
Finally, figure
We report molecular dynamics simulations of 2D complex plasma crystals with arbitrary shapes. A rigid walls assumption is used; it is especially suitable for right-angle crystals. Two-row crystals are produced with this simple and new method. It is the second method of simulating the two-row crystals and the first method is explained in our previous work.[24]
The parameters that have influence on inside structures of crystals are obtained. These parameters are the number of grains, grains charge, length and width of the crystal. We can prognosticate the internal structure of a crystal: square, hexagonal, or something else. In right-angle crystals, by increasing n, q, and b the number of grain rows increases and by increasing a the number of rows decreases. It is shown that boundary effects are of short range and boundaries do not change the internal structure usually.
We report long and narrow crystals that are a good candidate for electrostatic wigglers in FELs. Production of ideal crystals are complex and even in the computer, we can achieve the ideal two-row crystals approximately. Any little disordering at the grain position leads to a large irregularity in electric field. The electric field components Ex and Ey show the hidden details of these disorderings and also asymmetries that cannot be seen from grain positions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |
























