† Corresponding author. E-mail:
Cavity optomechanical systems provide powerful platforms to manipulate photons and phonons, open potential applications for modern optical communications and precise measurements. With the refrigeration and ground-state cooling technologies, studies of cavity optomechanics are making significant progress towards the quantum regime including nonclassical state preparation, quantum state tomography, quantum information processing, and future quantum internet. With further research, it is found that abundant physical phenomena and important applications in both classical and quantum regimes appeal as they have a strong optomechanical nonlinearity, which essentially depends on the single-photon optomechanical coupling strength. Thus, engineering the optomechanical interactions and improving the single-photon optomechanical coupling strength become very important subjects. In this article, we first review several mechanisms, theoretically proposed for enhancing optomechanical coupling. Then, we review the experimental progresses on enhancing optomechanical coupling by optimizing its structure and fabrication process. Finally, we review how to use novel structures and materials to enhance the optomechanical coupling strength. The manipulations of the photons and phonons at the level of strong optomechanical coupling are also summarized.
High quality-factor optical and mechanical modes can be coupled to each other through the radiation pressure. The cavity field localization results in a stronger optomechanical interaction, compared to that of a traveling light wave impacting on the macroscopic objects.[1] At the mesoscale, the eigenfrequencies of the cavity modes are sensitive to the variation of the effective cavity length, depending on the position of the movable mirror, which is modeled as a mechanical resonator. Based on these two aspects, modern cavity optomechanics mainly explores the interactions between the cavity field and the mechanical mode.[2] Any system, in which the mechanical motion gives a backaction on the dynamics of the cavity field (e.g., dissipation of the cavity fields) and vice versa, can be considered as a generalized optomechanical coupling system, and be included in the modern cavity optomechanics.[3]
Typical microcavities of the cavity optomechanical systems (COMS) are formed by, for example, Fabry–Pérot mirrors, whispering-gallery, photonic-crystal system or LC-oscillators. Although the geometric shapes of these cavities are different, the theoretical models, describing the optomechanical coupling, always have the same expression with the radiation pressure interaction. Here, the optical force is proportional to the intracavity photon number, which can be controlled by the power of the external control field.[4] When the power of the control field is strong enough, the optomechanical coupling can be linearized, and the optomechanical coupling strength, called as effective optomechanical coupling strength, can be enhanced by the control field. From then on, the COMS becomes a powerful platform to manipulate cavity field (photons) and mechanical motion (phonons), and is also applied for on-chip optical interconnect, precise measurement, and quantum information processing.[5–8]
In the classical regime, based on the linearized optomechanical coupling, many experiments have been devoted to studying cavity-optomechanically induced transparency (COMIT), which is similar to electromagnetically induced transparency (EIT), observed in atomic systems. The COMIT usually is from destructive interference between two different excitation pathways. This can be used to control light propagation on a chip, and to produce slow and fast light.[9] It even enables the complete stop or on-chip storage of the propagating light pulse via microfabricated optomechanical arrays.[10–16] Recently, optomechanical interactions are proposed to strongly break the reciprocity of light propagation. This motivates extensive study of magnetic-free and low-loss nonreciprocal devices,[17–19] such as optical isolators,[20–27] circulators,[28–32] and nonreciprocal phase shifter.[33] The nonreciprocal conversions between microwave and optical photons with optomechanical interaction are also explored for signal routing and protection.[34–36] Besides the control of classical light transmission, the optomechanical interaction can also be used to manipulate the mechanical properties, for example, controlling the phononic structures[37] and shifting mechanical frequency or decay rate by optical force.[38–40] Similar to the nonreciprocal light propagation, the optomechanical interaction can also induce a nonreciprocity of the mechanical motion (or called a sound wave).[41,42] Thus, the cavity optomechanical systems are powerful platforms to realize acoustic nonreciprocal devices,[43,44] such as sound isolators and acoustic circulators. By introducing multi-mode optomechanical interactions, e.g., two optical modes interacting with the same mechanical mode, one can achieve chiral cooling,[45] as well as phonon routing.[46,47] In particular, the mechanical resonator can be simultaneously coupled to optical and electronic cavities. This can be used for wideband wavelength conversion and energy transfer between microwave and optical fields.[48–57]
In the quantum regime, the linearized optomechanical systems have been used to generate nonclassical states for both the optical and mechanical modes. For example, it was recognized that cavity optomechanical systems can be used to generate squeezed light, which is closely related to quantum-limited displacement sensing,[58,59] owing to proposals for increasing the displacement sensitivity of large scale gravitational-wave observation with squeezed light.[60–65] Because the equivalence between an optomechanical system and Kerr systems,[66,67] the mechanism for generating squeezed light in optomechanics[68–71] is similar to that studied in Kerr nonlinear medium.[72,73] Recent researches show great interests in engineering a squeezed state of the macroscopically moving object,[74] i.e., squeezing the mechanical motion at large scales.[75,76] These are related to the study of decoherence of macroscopic quantum systems and the realization of ultrasensitive sensing of force and motion.[77] A crucial step for quantum manipulation of the macroscopic mechanical resonators is to cool the mechanical mode to its quantum ground state, in which the thermal noise is greatly reduced. Theoretical and experimental works show that the resolved sideband approach is a promising way to realize ground-state cooling.[78–96] In an opposite way, the optomechanical interaction can also be used to amplify the mechanical oscillation,[97–102] and generate phonon lasing with nonclassical phonon correlation.[103] The quantum-optical-control techniques are used to conditionally generate single-phonon Fock states of the mechanical resonator.[104] The nonclassical nature of these phonon states is verified by performing a Hanbury Brown and Twiss-type experiment without requiring full state reconstruction. Optomechanical interaction can also simultaneously modulate the optical field and the mechanical motion, for example, creating an entanglement between the mechanical oscillator and the cavity field.[105] The non-classical correlations between single-photons and -phonons from an optomechanical system were reported. These realize a full quantum protocol involving initialization of the resonator in its quantum ground state of motion and generation of correlated photon-phonon pairs.[106] Very recently, a cross-correlation technique was used to distinguish optically driven motion from thermally driven motion. This allows us to observe the quantum backaction up to room temperature.[107] The mechanical mode can interact simultaneously with two electromagnetic cavity modes with different wavelengths, (e.g., optical wave and microwave), and be used for the storage and transfer of a quantum state with high fidelity.[108–114] Fundamentally, the mechanical resonator can be optomechanically coupled to any electromagnetic mode in a wide frequency range.[115–119] Thus, the coherent-quantum-state transfer via optomechanical coupling allows one to overcome intrinsic limitations of both microwave and optical platforms.[120–122] These findings are very important for the study of exciting physics (e.g., quantum phenomena of macroscopic objects) and preparation of new generation quantum devices for applications in the real world.[123]
The studies reviewed above are mainly based on the linearized optomechanical coupling. Recently, much more attention has been paid to the nonlinear optomechanical coupling, which is a typical attribute of the cavity optomechanical systems.[124–126] Based on the optomechanical nonlinearity, manipulations of the optical field and the mechanical motion are widely studied for generating optical bistability[127–130] or multi-stability,[131–136] realizing chaotic optical fields with blue-sideband pumping,[137–139] slowing light with a high-order sideband.[140–152] For the manipulations of the mechanical resonator, the optomechanical nonlinearity has been explored to observe the stochastic resonance phenomenon and the chaos transfer between two optical fields.[153] When three-body interaction is considered, e.g., two mechanical modes are coupled to the same optical mode, these two indirectly coupled mechanical oscillators can be synchronized.[154–168] In the quantum regime, nonlinear optomechanical coupling strength is a key parameter for preparing nonclassical states of photons[169–171] and phonons.[172–177] Theoretical works reveal that optical antibunching[178–183] and photon blockade[184–188] can be observed in the single-photon strong optomechanical coupling regime, where the nonlinear optomechancial coupling strength is larger than the decay rates of both the cavity field and the mechanical mode. This is also required when other nonclassical states (e.g., NOON state) are engineered in optomechanical systems.[189–200] There are many studies for fundamental physics under the strong coupling condition, including, e.g., the observations of phonon number jump[201–203] and phonon-phonon Josephson effect.[204,205] Motivated by the importance of strong coupling for the single-photon optomechanics, great efforts have been made to achieve strong optomechanical coupling. However, it is still a great challenge for experiments. In this article, we will review the mechanism that was theoretically proposed and experimentally studied to enhance the single-photon optomechanical coupling strength for the COMS. We hope that the works, summarized here, could motivate more fantastical ideas and experimental improvements to achieve strong optomechanical coupling in the future.
The paper is organized as follows. In section
As schematically shown in fig.











Because the displacement of the right mirror (mechanical resonator) is much smaller than the cavity length, the cavity frequency modulated by the position of the movable mirror can be treated with Taylor expansion, that is


Applying a unitary transform 



To explore the quantum nonlinear behavior of optomechanics, the effects of the radiation pressure interaction should be observed at the single-photon level. This requires that the single-photon optomechanical-coupling strength g exceeds the cavity decay rate κ. Here we review several theoretical proposals to enhance optomechanical coupling strength for potential applications, such as nonclassical photon (phonon) state preparation, single-photon source, and the quantum state reconstruction.
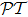
The system with 








Considering a mechanical resonator optomechanically coupled to the optical field of the passive cavity in 




The Hamiltonian in Eq. (








The optomechanical interaction can be used to generate squeezed light. Interestingly, it has been proposed in Ref. [217] that the squeezed cavity mode can be used to enhance the optomechanical coupling strength. As schematically shown in fig.
Besides squeezed state enhanced optomechanical coupling, the single-photon optomechanical interaction can also be enhanced via a parametric driving field applied to the mechanical resonators. This scheme results in an exponential enhancement of the single-photon coupling constant g, and the enhancement can be controlled by the amplitude and detuning of the driving field.[236] It enables true quantum nonlinearity even when the single-photon coupling g is much smaller than the cavity-damping rate κ.
The optomechanical coupling can also be enhanced by indirect coupling, e.g., mediated by two-level quantum emitters, as schematically shown in fig.
Recently, superconducting quantum interference devices (SQUID) were explored for all-electrical realizations of analogs to optomechanical systems.[245] Two transmission-line resonators (resonator A, and B) are coupled to each other through the SQUID terminating resonator A.[246] The coupling mechanism is that the magnetic field in resonator B, threading the SQUID loop of resonator A, changes the phase across the SQUID. This introduces an optomechanical-type interaction. Here, the effective optomechanical coupling strength is tunable, and depends on the properties, including the bias conditions of the SQUID and the detailed geometry of the coupling (e.g., inductive coupling or galvanic coupling). The device is a promising candidate for realizing the single-photon strong coupling, and could be used in microwave-photon-based quantum simulation.[247]
Very recently, ultrastrong coupling between the two-level systems and cavity fields has been realized in, for example, semiconducting and superconducting devices, especially towards the deep-strong coupling where the interaction strengths are comparable to the bare frequencies of the light and the matter.[248] In the deep-strong coupling regimes, the states of the whole system are dressed by virtual photons,[249–254] which are negligible in weak and strong coupling regimes. It has been proposed that such virtual photons can be further explored to enhance the single-photon optomechanical coupling strength. The system is now a hybrid device of a matter, cavity, and mechanical resonator, where a mechanical mode is coupled to a cavity-QED system. The matter represents a general two-level system, including superconducting qubit, quantum dot, and NV-center. The interaction between the cavity field and a matter degree of freedom (modeled as a two-level system) is described by the quantum Rabi model with anti-rotating wave term. A recent work[255] shows that the photons, dressing the ground state of the strongly coupled cavity-QED system, can induce single-photon optomechanical coupling strength through the virtual radiation-pressure effect. Moreover, a modulation of the optomechanical interaction is also introduced to observe variations similar to the Casimir force.[256–261] As a result, one can observe the amplified ground-state occupation, where the displacement can be resolved from thermal and vacuum fluctuations. This requires a sufficiently large optomechanical coupling. Such a device may also allow an effective quantum nondemolition measurement.
Another promising approach to enhance single-photon optomechanical coupling is to exploit collective optomechanical interactions, where many mechanical resonators are embedded to a single optical cavity.[262] This approach is similar to that using an ensemble of cold atoms, instead of a single atom, to enhance the optical-matter coupling strength. As schematically shown in fig.
In Ref. [263], the authors showed in detail that the collective motion of a periodic array of identical scatterers, placed inside a cavity field, can couple very strongly to the optical field. In this configuration, the array is transmissive in contrast to the usual reflective optomechanics approach. Regardless of whether the scatterers are atoms or mobile dielectrics, the coupling strength under this configuration scales superlinearly (
Optomechanical crystals are also deeply explored to enhance the coupling between the optical field and the mechanical resonators at the nanoscale. In optomechanical crystals, imperfections induce extra loss of energy. This reduces the optomechanical coupling strength. In Ref. [264], the authors quantify the role of disorder in a paradigmatic one-dimensional optomechanical crystal with full phononic and photonic band gaps, and anti-intuitively find that such disorder can be exploited as a resource to enhance the optomechanical coupling beyond engineered structures. This study provides a new tool to enhance the single-photon optomechanical coupling strength.
For a conventional optomechanical system, where a mechanical membrane is inserted into an optical Fabry–Pérot cavity, the optomechanical coupling strength is proportional to the electric susceptibility of the membrane resonator. Ref. [265] shows a method to enhance the optomechanical coupling via the refractive medium, which results in a tunable susceptibility. In particular, a tunable ultra-large refractive index without absorption can be obtained by doping atoms or spins into the membrane. If these atoms or spins are driven appropriately, then the giant susceptibility without additional absorption can greatly enhance the optomechanical coupling strength. Possible implementation of this scheme is proposed by using Er3+ dopants at low temperature, and Cr3+ in a Ruby membrane at room temperature. This scheme can also support a tunable and wide-range coupling strength.
In the microwave domain, it has been proposed to realize single-photon strong or ultrastrong optomechanical coupling by using a dynamical Casimir effect. References [266] and [267] describe a hybrid optomechanical scheme involving a SQUID. This structure has been proposed and deeply explored as a displacement detector,[268–271] but without the cavity mode. However, in Ref. [266], it was evaluated in the context of ultrastrong coupling or time-dependent external flux driving. By modulating an external flux applied to the SQUID loop, the variation of effective inductance of the SQUID modulates the frequency of the cavity mode non-adiabatically. This results in photon production from the quantum vacuum, and can be viewed as a nonlinear 
Benefiting from the development of the modern micro/nono-fabrication, one can design and fabricate the optical cavity and mechanical resonator with a very high Q-factor. The structure of the cavity optomechanical systems becomes much richer and the optomechanical coupling strength is more controllable. In this section, we review experimental progresses on engineering optomechanical coupling in different types of optomechanical systems, including Fabry–Pérot, whispering-gallery, photonic-crystal, and electromechanical systems. Engineering the optomechanical coupling strength by using novel material is also summarized here. To give an intuitive understanding of the importance of the optomechanical coupling strength, we review its application, for example, controllable photon or phonon transport with the improvement of the coupling strength.
The optomechanical interactions have been well studied in the typical Fabry–Pérot cavity structure, in which one mirror is fixed while the other one can move and works as the mechanical oscillator. In 1983, the optomechanics based on Fabry–Pérot cavity structure was proposed and realized,[279] where the frequency of the mechanical resonator is 1 Hz. The authors studied the typical hysteresis cycle of transmitted powers, also known as the bistable behavior induced by the radiation pressure. Due to the strong classical noise of laser and the weak radiation pressure, the experiment has not reached the quantum regime. The modern cavity optomechanical experiment began in the late 90s, based on the improvement of micro/nano fabrication technology. It uses the narrow linewidth laser and a high-quality-factor cavity to enhance the optical backaction. Besides the optical aspect, the mechanical resonators with high quality factor and frequency are also fabricated to reduce the Brownian noise. These advancements make it possible to do experiments approaching the standard quantum limit.[280–282]
To further enhance the mechanical frequency, a silicon doubly-clamped (1 mm×1 mm×60 mm) beam with a mirror coated upon its surface (working as a back mirror of a single-ended Fabry–Pérot cavity) was designed and fabricated.[283] The effective mass of the mechanical resonator is 





Towards this direction, an all-optical trap for a gram-scale mirror structure[286] and the self-cooling of the micromirror resonator in a cryogenic environment[287] are studied. Moreover, the processing technology of the micromirror was further developed to obtain a high-quality-factor mechanical resonator with exceptionally low intrinsic absorption for the optical modes.[288,289] The frequency of fundamental mechanical modes was improved to approach MHz. The mechanical quality factor reaches up to 
With these improvements, opto-mechanical normal mode splitting was observed. This provides unambiguous evidence for achieving strong coupling between a micromechanical resonator and an optical cavity field.[88] Based on the linearized strong optomechanical coupling strength, the mechanical quantum state tomography was demonstrated using short optical pulses.[172,290] Despite that the mechanical resonator was initialized in a thermal state, this structure allows us to observe the quantum features of a mechanical oscillator. Further, the preparation and reconstruction of mechanical quantum states were experimentally studied.[291] In 2015, Kalman filters for optimal state estimation of cavity optomechanical systems were also realized.[292] This laid a fundamental basis for preparation, measurement, and real-time control of macroscopic quantum states.
Besides the experimental setup that the mirror acts as the mechanical resonator to construct the optomechanical system, the optomechanical system can also be formed by placing a mechanical membranae inside the Fabry–Pérot cavity. It means that the mechanical resonator has been separated from the optical cavity, this leads to flexible and individual control of each component. The optomechanics was demonstrated in a cavity modulated by an SiN membrane (1 mm×1 mm×50 nm) on a silicon chip inside the cavity.[293] The lowest resonance frequency of such membranae is 134 kHz, with an effective mass 40 ng. These parameters correspond to the mechanical quality factor up to 
To further reduce the noise of the laser, a passive filter cavity was used to remove classical laser noise in a cryogenic optomechanical system. The future requirements for laser cooling of the mechanical element close to its ground state were discussed.[295] After that, reference [296] reported measurements of the motion sidebands, produced by a mechanical oscillator, which is cooled close to its quantum ground state with the resolved-sideband cooling scheme. The mechanical mode was fabricated with an effective mass 43 ng, a resonant frequency 705.2 kHz, and a mechanical linewidth 0.1 Hz, while the optical mode has a linewidth of 165 kHz with an optical finesse 


Another advantage of the Fabry–Pérot cavity optomechanical system is its powerful ability to construct the hybrid optomechanical devices with other quantum systems, e.g., cold atomic ensembles. A hybrid optomechanical system was realized by coupling the ultracold atoms to a micromechanical membrane.[298] These atoms were first trapped in an optical lattice, driven by a laser retroreflection from the membrane surface. The coupling between membrane vibrations and atomic motion was induced by the lattice laser. The dissipative rate of the membrane could be engineered by coupling to the laser-cooled atoms. With atomic hybridization, the cooling of the membrane vibrations from room temperature to 650±230 mK has been reported.[299] By coupling the membrane vibrations to the atomic motion, mature atomic laser cooling technology makes it possible to relax the constraints of pure cavity optomechanical or feedback cooling techniques.
These investigations indicate that the Fabry–Pérot cavity optomechanical system becomes more and more mature for controlling both the optical field transport and mechanical oscillation. The optomechanically induced transparency was demonstrated in a cavity optomechanics formed by a semitransparent membrane in the middle of a Fabry–Pérot cavity.[300] A weak probe field was completely transmitted when the red detuning of the pump field equals to the frequency of the mechanical resonator. The COMIT can be used to delay the transport of the probe light. The similar but totally different phenomenon is electromagnetically induced amplification. It has also been observed with a blue sideband detuning pumping. A topological energy transfer in an optomechanical system was proposed and realized in the Fabry–Pérot cavity optomechanical system to control the transport of phonons.[301] The adiabatic topological operation allows for non-reciprocal energy transfer between two different mechanical modes.
In order to overcome the extra dissipation induced by suspended coating mechanical oscillator, mechanical oscillators with high-quality-factor were further explored. For example, a monolithic high-reflectivity cavity mirror from a single silicon crystal, avoiding the coating thermal noise problem, was designed and fabricated.[302] Additionally, to obtain a high-frequency mechanical resonator, a micropillar geometric shape was designed.[303] This structure can support mechanical mode with high-quality-factor (up to 

The Whispering–Gallery–Mode cavity takes advantage of the long lifetime of photons and small mode volume. Due to total reflection, the light transports along the circumferential direction of the toroid, and the vector of its momentum becomes opposite. This results in a radiation pressure on the cavity wall. The Whispering–Gallery–Mode cavity optomechanical devices provide a powerful platform for the experimental study of dynamical optomechanical interaction, which could be used to manipulate the transport of the optical field and the mechanical motion. Here we review the improvement of optomechanical interaction by engineering its geometric structure and the fabrication process.
In Ref. [311], the excitation of the mechanical mode in the Whispering–Gallery–Mode cavity was observed. The radiation pressure was the excitation source of the observed mechanical oscillations. The reported effective mass of the mechanical resonator in this device is about 50 ng. The frequency and decay rate are 4.4 MHz and 1.25 kHz, respectively. The quality factor of the mechanical resonator reaches 3500. The decay rate of the optical field in a microtoroid is about 10 MHz. It has been proposed that the resolved sideband cooling is a promising way to cool the mechanical motion to the ground state. Such a proposal requires that the frequency of the mechanical mode should be larger than the decay rate of the optical cavity to suppress the heating rate and obtain a net cooling rate. Reference [312] proposed a spoke-anchored toroidal resonator to enhance the mechanical frequency and reduce the clamping losses of the mechanical resonator. The effective massive of the mechanical resonator is also reduced due to its spoke structure. This results in a low-pump threshold excitation of the mechanical motion. Both of these improvements in turn result in a higher optomechanical coupling strength compared to that of the conventional microtoroid cavity. Devices, fabricated in the spoke-anchor manner with radius 515 mm in this work, exhibits optomechanical coupling rates as high as 3.4 kHz for a mechanical resonance frequency of 78 MHz, an optical decay less than 10 MHz, and a critically resolved-sideband factor for ratio 11 between the mechanical frequency and the cavity decay rate. Although the single-photon optomechanical coupling has been improved through spoke-anchored design, it is still much smaller than the decay rate of the cavity, corresponding to the weak coupling regime. An externally strong pump is tailored to obtain a strong and linearized optomechanical coupling. As a result, a quantum-coherent coupling between the optical photons and the mechanical motion has been observed, at the same time, the mechanical oscillator was cooled to an average occupation of 1.7 motional quanta.
To further improve the coupling strength and mechanical quality factor, the geometric dimensions can be optimized by reducing the thickness of both the spokes and the pillars.[313] Such a device consists of a toroidal boundary, supported by four spokes. The outer torus is connected to the silicon chip via silica bridges. This design can decouple the radial motion from the clamping area in the centre of the disk, resulting in an ultralow dissipation rate. The measured mechanical quality factor is up to 
Another method to enhance the optomechanical coupling is to separate optical cavity from mechanical resonator. This scheme presents maximum flexibility to engineer the parameters of the optical field and mechanical resonator simultaneously. As reported in Ref. [48] a doubly clamped, high-stress Si3N4 nanomechanical beam is coupled to a silica microdisk resonator via evanescent near-field. The bevel for the edge of the disk was optimized to minimize the decay rate of the cavity field through finite-element simulation of the electromagnetic field distribution of the fundamental optical mode, confined in the microdisk resonator. The Si3N4 material holds a high elastic modulus and may be the best material to make mechanical resonator with high quality factor. The beam, used in this work, has dimensions of 90 mm×700 nm×100 nm, and the microdisk has a diameter of 76 mm. Under this structure, the optomechanical coupling strength was improved to 
Besides the evanescent near-field optomechanical coupling, the optical gradient force was also explored to enhance the optomechanical coupling strength.[38,314,315] The double-disk was separated by a nanoscale gap region on a silicon chip for cavity optomechanics. The structure features a gradient-force-induced optomechanical coupling, which enables improvement of the optomechanical coupling strength. As reported in Ref. [154] two double-disk optomechanical cavities are coupled closely enough in space to induce energy transfer between these two double-disk optomechanical systems. As a result, the frequency synchronization of two mechanical oscillators was observed under distance by a few hundred nanometers. Here, the mechanical oscillators are not directly coupled. Instead, the optical cavity fields work as the bus to connect these two resonators. These results pave a path toward reconfigurable synchronized oscillator networks.[163,316]
Combining the spoke structure and optical gradient force in a double disk,[317] a novel optomechanical system was then proposed and the optomechanical coupling strength is further improved. In Ref. [318], a resonant cavity sensitive to the optical gradient forces, was designed. In this design, two vertically stacked ring cavities are held by a very thin pedestal. This structure results in a high sensitivity even to small changes in the distance between the rings. The spokes are designed to enhance the mechanical rubbing of the cavity, and to increase the sensitivity to the optical forces between the rings. The gap between the top and the bottom resonator is about 640 nm. The Si3N4 material is chosen to introduce a relatively small refractive index. This makes strong optomechanical coupling possible for relatively large gaps between the top and the bottom resonators. As a result, the optomechanical coupling strength is greatly improved and transverse mode profiles are changed into symmetric and antisymmetric combinations which lead to two supermodes with distinct resonant frequencies.
With the increase of the optomechanical coupling strength, the Brillouin-scatter effect becomes much more important, and is widely explored in micro bottles[319] and microspheres.[23] Required by the momentum and energy conservation, Brillouin-scattering induced transparency was explored to generate ultralow-power and footprint slow-light. It also enables non-reciprocal light transport. In Ref. [320], a multi-channel cavity optomechanical system was designed and fabricated with two separated wave guides. This structure allows the control of non-linearity of optical force, all-optical signal amplification and wavelength reuse. A bovine-eye like cavity system was also reported with a high mechanical quality factor and gigahertz frequency.[321] By using diamond materials, the system can be hybridized with spins and further explored to study many-body interactions.[322]
In this section we will review recent developments for improving optomechanical interaction in photonic crystal systems. Besides the optical cavities, the mechanical resonators can also be fabricated in the nano-structure film through periodic patterning.[323] This results in a localized photon-phonon interaction in a single device. Three main aspects motivate the developments of optomechanical crystal. (i) The periodic nanostructures support a high quality mechanical resonator with small mass. (ii) The localized optical and mechanical mode could induce a strong optomechanical coupling. The basic mechanism is similar to that using collective mechanical mode to enhance the optomechanical strength. (iii) Flexible photonic crystal drilling provides more freedom for developing complex optomechanical structure. In addition to the basic study of two-body linear optomechanical interaction, e.g., state conversion and storage, the optomechanical crystal would also allow the observation and study of non-traditional collective dynamics.
In Ref. [324], the zipper cavity optomechanical crystal was designed and fabricated. The mechanical resonator has a mass of pg order of magnitude. Compared to the Fabry–Pérot cavity and Whispering–Gallery–Mode cavity, the mechanical mass has been greatly reduced. The optomechanical coupling is exponentially proportional to the slot gap between the beams. Under the zipper-like structure, the in-plane differential motion of the nanobeams is strongly coupled to the optical cavity field, whereas common motion is nearly decoupled. Especially, the beam widths are on the order of the wavelength of light, resulting in an optomechanical coupling strength several orders of magnitude larger than that obtained in the Fabry–Pérot cavity or Whispering–Gallery–Mode structures. In addition, a flexible design of the geometry shape can greatly vary the mechanical stiffness and frequency, in turn, resulting in a stronger optomechanical coupling strength. A silicon nitride (Si3N4) film, having a thickness of 400 nm, was first deposited on a silicon wafer using a low pressure chemical vapor deposition method. A zipper-shaped pattern was then generated by the electron beam lithography. The patterned zipper cavity consists of beams of length 

With the development of the zipper cavity, an accordion-like optomechanical crystal was fabricated by patterning holes in a quasi-one-dimensional nanobeam.[325] Such a structure can support much more abundant optical and mechanical modes with high quality factor. The mechanical frequency is improved to gigahertz. The experiment demonstrated an optomechanical coupling between 200-THz photons and 20-GHz phonons in a planar optomechanical crystal. The breathing mode, accordion mode, and Pinch mode were calculated via finite element methods. The mechanical spectroscopy of this device was detected through a taper waveguide coupled to the optical mode. The basic parameters for different mechanical modes were obtained and had a good correspondence to the results obtained from simulations. The frequency for the pinch mode is 0.8 GHz, with quality factor less than 103. The frequency for the accordion mode is 1.4 GHz with quality factor about 103. The breathing has a frequency 2.25 GHz and the quality factor is less than 
To further increase the optomechanical coupling in photonic crystal devices, the slot-mode-coupled optomechanical system was designed and fabricated. In Ref. [326], the quality factor of the optical mode was improved and became larger than 106. The optical field is evanescently coupled to a localized mechanical mode with gigahertz. The device was still designed in a nanobeam structure, whereas the pore sizes were changed. The optical and mechanical modes can be free of mutual interferences by using separated nanobeams to provide the optical cavity and mechanical resonator, independently. Such structure supports typical mechanical mode with frequency 1.38 GHz and its effective mass is only 1.8 pg. The size optimization in turn enables a large zero-point optomechanical coupling strength, for example, the single-photon optomechanical coupling strength is larger than 300 kHz in an Si3N4 nanobeam at 980 nm and about 900 kHz in an Si nanobeam at 1550 nm. The large coupling strengths to GHz mechanical resonators was achieved in the Si3N4 nanobeam. This paves the way for wide-band optical frequency conversion. The Si3N4 material has a broad optical transparency window and allows it to operate throughout the visible and near-infrared. For example, a frequency conversion between 1300 nm and 980 nm, using two optical nanobeam cavities coupled either side to the breathing mode of a mechanical nanobeam, has attracted a great deal of attention.
Recently, two-dimensional phononic-photonic band gap optomechanical crystal, instead of one-dimensional periodic mechanical structures, has been proposed to expand the mechanical frequency to microwave X-band and to introduce a strong optomechanical coupling. These two-dimensional-planar structures can support photonic and phononic band gaps simultaneously.[327] Another kind of two-dimensional device demonstrated a planar snowflake structure.[328] The snowflake lattice was used to tailor the properties for both the optical fields and the acoustic waves. The strong optomechanical coupling, that exists between localized optical and mechanical modes, was characterized through two-tone optical spectroscopy. The mechanical frequency is about 9.3 GHz, and the single-photon optomechanical coupling strength is evaluated as 220 kHz. The snowflake 2D light optomechanical structure can also be expanded to realize multibody photon and acoustic interaction. It could allow us to capture and store optical pulses, or filter and route optical signals through microwave photons. Benefiting from the snowflake 2D structure, the thermal conductivity of the mechanical vibrator can be greatly reduced. This platform allows the studies of the macroscopic quantum physics in future.
The designed 2D-snowflake structure can also effectively reduce the decay rate of the mechanical resonator. Thus, it has been used to optimize the optomechanical crystal cavity with an acoustic radiation shield.[329] This results in a nanobeam with an experimentally realized intrinsic mechanical frequency at 5.1 GHz, and a mechanical Q-factor of 6.8×105 measured at 10 K. The single-photon optomechanical coupling strength has also been improved to 1.1 MHz. Besides the conventional Si and Si3N4 materials, the diamond material has also been used to engineer the optomechanical interaction.[330] The extremely high stability and hardness of the diamond provide a powerful platform for measuring the signal under extreme conditions. On the other hand, the NV center has been widely explored for solid-state quantum information processing. So, the diamond optomechanical crystal could be further explored to study the hybrid optomechanical system with spins.
Microwave cavity electromechanics is a part of nano-electromechanics and micro-electromechanics; it mainly studies the interaction between electric field and mechanical motion in the microwave domain. Microwave cavity electromechanical systems are effective platforms to explore and interpret macroscopic quantum behavior using mechanical oscillators. Cavity electromechanics was originated from circuit quantum electrodynamics (cQED)[248] and developed for observing the quantum effects in nano-elctromechanical systems and exploring gravitational waves. At the same time, the quantum characters of microwave fields have been experimentally demonstrated using cQED. Such as, Josephson junctions are used to create artificial atoms (qubits) and design superconducting resonators with tunable frequencies. The coherent coupling between single microwave photon and qubit has already been experimentally realized.[248] This leads to a general considerations of achieving strong interaction between microwave photons and mechanical motion, where the quantum characters of mechanical motion and microwave radiation pressure could be observed. In practice, a superconducting circuit with a mechanical element is typically associated with the Hamiltonian that describes a Fabry–Pérot cavity optomechanical system. Mechanical motion changes the resonant frequency of the superconducting circuit and in turn introduces the dispersion coupling between microwave photon and mechanical resonator.
The microwave cavity-electromechanical system has many attractive features. For example, the superconducting circuit is compatible with current semiconductor technology. It facilitates the integrated circuit design and production. The circuit resonator can be designed flexibly and the structures of the mechanical oscillators (e.g., nanobeam and tympanic-membrane) are diverse. These features allow the superconducting microwave circuit to generate specific optomechanical interactions, for example, the qubit mediated nonlinear and strong coupling. The electromechanical systems are also good platforms to study multimodes optomechanical interactions. The localization of interacting photons, phonons, or photon-phonon polaritons in mulitmodes optomechanical systems also recently emerges. With photon and phonons, exotic phenomena, thought to exist only in strongly interacting electronic systems (such as Mott transitions, Fractional Hall effect, spin-charge separation, interacting relativistic theories, and topological physics) can be reproduced and understood in more detail. The quantum simulator with photon-phonon polaritons is also a relatively new and fantastic research subject. Since the microwave cavity electromechanical system can be compatible with cryogenic technology, the experiment can be carried out at low temperatures (usually less than 1 K). This greatly eliminates the impact of random thermal fluctuations upon mechanical quantum states. Similarly, the microwave cavity, formed by the lithographic superconducting film, is very stable compared to the optical microcavity, so the frequency locking and stabilization techniques can also be avoided.
Here we introduce several typical achievements in cavity-electromechanical systems, e.g., preparation and transfer of quantum states of microwave fields or mechanical modes. In Ref. [331], a capacitive elbow coupler was used to couple the microwave photons and measure the nanomechanical motion. The microwave cavity was formed by a 5-


To improve the electromechanical coupling strength, in Ref. [332], the high stress SiN mechanical resonator was coated with Al. The nano-mechanical oscillator interacted with the superconducting microwave resonator through the capacitive coupling. The high stress SiN-nano-mechanical oscillator has a very low dissipation rate, and its quality factor can reach 106. The mechanical resonator has a resonant frequency at 5.57 MHz and a decay rate of 25 Hz. The resonant frequency of the superconducting microwave cavity is 5.01 GHz with the decay rate 494 kHz. The single-photon coupling strength has been increased to 7.5 kHz/nm. The quantum non-destructive measurement of the nanomechanical oscillator was then experimentally observed. With such electromechanical structure, thermomechanical vibrations at 25 mK were measured and a number of about 20 phonons were obtained in the equilibrium.[333] The frequency of the nanometer mechanical resonator is as high as 67 MHz with the quality factor about 
In order to further improve the coupling strength of the optical field and mechanical resonator, the tympanic capacitive mechanical oscillator was designed.[334] The single-photon coupling intensity 100 MHz/nm is two orders higher than that obtained in Ref. [294]. The intrinsic frequency of the optical cavity is 7.5 GHz with a decay rate 170 kHz. The frequency of the tympanic mechanical vibrator is 10.69 MHz with the decay rate of 30 Hz and a quality factor of 
To further reduce the mass and improve the mechanical frequency, a superconducting cavity mechanical system in the silicon insulator platform[335] was designed and fabricated. The mechanical quality factor was also increased to 
In general, the cavity-electromechanical system plays an important role in the control of the microwave signal transport, mechanical oscillator cooling, macroscopic quantum state preparation, etc. The coupling of the microwave cavity electromechanics with the optical cavity will further extend the application of the system to quantum information processing, for example, coherent quantum state transfer. High compatibility with low-temperature environments also makes it easy to integrate with the superconducting quantum circuits.[248] This supports a powerful platform to construct the hybrid quantum system.
In Table
| Table 1.
Summary of the parameters for current optomechanical experiments in microwave and optical domains. In the table, |
Besides conventional mechanical resonators, two dimensional materials,[342] ferromagnetic magnons,[343] plasmonic molecules,[344] and levitate particles[345] were also extensively explored to construct novel optomechanical systems. The superfluid optomechanical systems, consisting of a miniature optical cavity filled with superfluid helium, support strong optomechanical coupling, which is close to serval Kilohertz.[346,347] However, the decay rates of the optical modes are enhanced when the cavity is soaked into the superfluid helium,[348,349] which is harmful for achieving the strong single-photon optomechanical coupling. To overcome this problem, the superfluid helium resonator was coupled into the microwave cavity[350,351] with very low loss, instead of the optical ones. The acoustic motion of superfluid He is parametrically coupled to the superconducting microwave resonator, and thus a gram-scale and sideband-resolved optomechanical system is formed.[352] In the microwave domain, the superfluid He resonator offers extremely low losses with quality factors as high as 1.4 
By engineering an optomechanical structure and using novel material, great advances have been achieved on enhancing the optomechanical coupling strength for different types of optomechanical systems and there is a great possibility to realize strong single-photon coupling in future. These advances will enable new avenues to understand cavity optomechanics and to detect gravitational waves in small scale.[356]
The rapid progress in cavity optomechanics has been made in recent years with great achievements, including ground-state cooling of the mechanical resonator, optomechanical induced transparency, squeezed optical field, coherent state transfer, and photon-phonon entanglement. Most of the applications reported now are mainly based on the linearized optomechanical coupling, which is always induced by a strong control field. The intrinsic nonlinearity of optomechanical interaction has recently attracted a great deal of attention, especially at the single-photon level. Theoretical studies reveal a number of important applications for the quantum information process, for example, non-classical states preparation, single-photon source, phonon number transition, quantum state reconstruction, and multiphonon process, in the strong single-photon optomechanical coupling regime, where the coupling strength is comparable to the mechanical frequency, and at least to be larger than the decay rates of both the cavity field and the mechanical mode. In experiment, most of the optomechanical platforms hold a weak optomechanical coupling strength, except for the BEC-cavity optomechanical system. Thus, engineering optomechanical interaction towards strong coupling is a promising and urgent project.
In principle, two research directions should be further explored to realize this goal. One is to enhance the single-photon optomechanical strength. Along this direction, many talent mechanisms have been proposed and shown the great enhancement of the optomechanical coupling strength. Most of these methods show the possibility to be experimentally realized in the near future. Another direction to achieve single-photon strong coupling is to engineer the device structure and materials. Great efforts have been made to optimize the device structure (e.g., spoke, double disk, snowflake, and accordion-like patterns) in conventional Fabry–Pérot, Whispering–Gallery–Mode, Photonic-crystal, and LC-resonator cavity optomechanical systems. New materials include plasmon nanomechanics, superfluid helium films, molecular vibration, monolayer or multilayer graphene, carbon nanotube, optically levitated nanosphere, NV-center, and ferromagnetic magnons. Benefiting from optimizations of the structure and material parameters, the single optomechanical coupling strength for both the contentional and novel optomechanical systems has been greatly improved and shown great potential towards the strong regime.
Although realization of the strong single-photon optomechanical coupling in experiments still challenges current technology, important applications with the improvements of optomechanical coupling strength have extensively been explored, e.g., optomechanical nonlinearity induced optical chaos, mechanical synchronization, slowing light with high-order sidebands, which are summarized in the corresponding sections. We hope the works reviewed in this paper can further motivate more great ideas and experimental designs to achieve strong single-photon optomechanical coupling, which plays a key role in applications of quantum communication, sensing, and computing.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] | |
| [119] | |
| [120] | |
| [121] | |
| [122] | |
| [123] | |
| [124] | |
| [125] | |
| [126] | |
| [127] | |
| [128] | |
| [129] | |
| [130] | |
| [131] | |
| [132] | |
| [133] | |
| [134] | |
| [135] | |
| [136] | |
| [137] | |
| [138] | |
| [139] | |
| [140] | |
| [141] | |
| [142] | |
| [143] | |
| [144] | |
| [145] | |
| [146] | |
| [147] | |
| [148] | |
| [149] | |
| [150] | |
| [151] | |
| [152] | |
| [153] | |
| [154] | |
| [155] | |
| [156] | |
| [157] | |
| [158] | |
| [159] | |
| [160] | |
| [161] | |
| [162] | |
| [163] | |
| [164] | |
| [165] | |
| [166] | |
| [167] | |
| [168] | |
| [169] | |
| [170] | |
| [171] | |
| [172] | |
| [173] | |
| [174] | |
| [175] | |
| [176] | |
| [177] | |
| [178] | |
| [179] | |
| [180] | |
| [181] | |
| [182] | |
| [183] | |
| [184] | |
| [185] | |
| [186] | |
| [187] | |
| [188] | |
| [189] | |
| [190] | |
| [191] | |
| [192] | |
| [193] | |
| [194] | |
| [195] | |
| [196] | |
| [197] | |
| [198] | |
| [199] | |
| [200] | |
| [201] | |
| [202] | |
| [203] | |
| [204] | |
| [205] | |
| [206] | |
| [207] | |
| [208] | |
| [209] | |
| [210] | |
| [211] | |
| [212] | |
| [213] | |
| [214] | |
| [215] | |
| [216] | |
| [217] | |
| [218] | |
| [219] | |
| [220] | |
| [221] | |
| [222] | |
| [223] | |
| [224] | |
| [225] | |
| [226] | |
| [227] | |
| [228] | |
| [229] | |
| [230] | |
| [231] | |
| [232] | |
| [233] | |
| [234] | |
| [235] | |
| [236] | |
| [237] | |
| [238] | |
| [239] | |
| [240] | |
| [241] | |
| [242] | |
| [243] | |
| [244] | |
| [245] | |
| [246] | |
| [247] | |
| [248] | |
| [249] | |
| [250] | |
| [251] | |
| [252] | |
| [253] | |
| [254] | |
| [255] | |
| [256] | |
| [257] | |
| [258] | |
| [259] | |
| [260] | |
| [261] | |
| [262] | |
| [263] | |
| [264] | |
| [265] | |
| [266] | |
| [267] | |
| [268] | |
| [269] | |
| [270] | |
| [271] | |
| [272] | |
| [273] | |
| [274] | |
| [275] | |
| [276] | |
| [277] | |
| [278] | |
| [279] | |
| [280] | |
| [281] | |
| [282] | |
| [283] | |
| [284] | |
| [285] | |
| [286] | |
| [287] | |
| [288] | |
| [289] | |
| [290] | |
| [291] | |
| [292] | |
| [293] | |
| [294] | |
| [295] | |
| [296] | |
| [297] | |
| [298] | |
| [299] | |
| [300] | |
| [301] | |
| [302] | |
| [303] | |
| [304] | |
| [305] | |
| [306] | |
| [307] | |
| [308] | |
| [309] | |
| [310] | |
| [311] | |
| [312] | |
| [313] | |
| [314] | |
| [315] | |
| [316] | |
| [317] | |
| [318] | |
| [319] | |
| [320] | |
| [321] | |
| [322] | |
| [323] | |
| [324] | |
| [325] | |
| [326] | |
| [327] | |
| [328] | |
| [329] | |
| [330] | |
| [331] | |
| [332] | |
| [333] | |
| [334] | |
| [335] | |
| [336] | |
| [337] | |
| [338] | |
| [339] | |
| [340] | |
| [341] | |
| [342] | |
| [343] | |
| [344] | |
| [345] | |
| [346] | |
| [347] | |
| [348] | |
| [349] | |
| [350] | |
| [351] | |
| [352] | |
| [353] | |
| [354] | |
| [355] | |
| [356] |



















