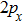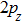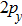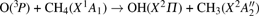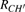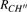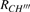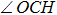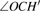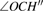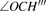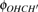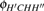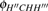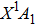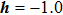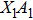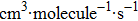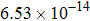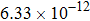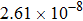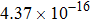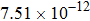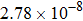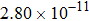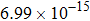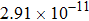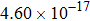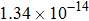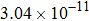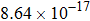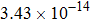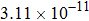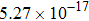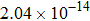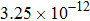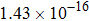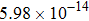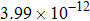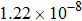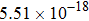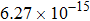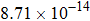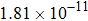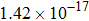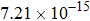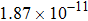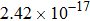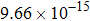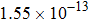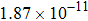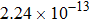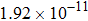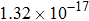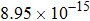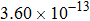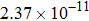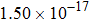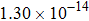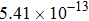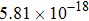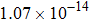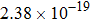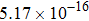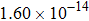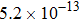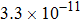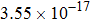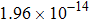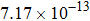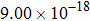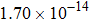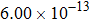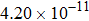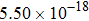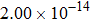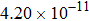† Corresponding author. E-mail:
This paper represents an attempt to extend the mechanisms of reactions and kinetics of a methane combustion reaction. Three saddle points (SPs) are identified in the reaction 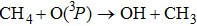
The reaction of ground-state atomic oxygen with methane is an important initial step of oxidation in combustion processes.[1–5] Since methane is the simplest organic fuel and stored in not only various minerals but also atmosphere as the most abundant hydrocarbon, its combustion has attracted considerable interest, both from experimental and theoretical perspectives.[6–18] The 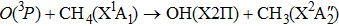
The title reaction has been extensively investigated experimentally, and a considerable body of work was devoted to the experimental characterization of the OH molecule produced in related processes via molecular beams, like the reactions of O atom with saturated, unsaturated, cyclic and aromatic hydrocarbons, in which reactions a small amount of OH radical rotational excitation has been found.[26,27] It was interpreted as resulting from a direct reaction mode and a favored near-collinear O–H–C approach of the O atom to the C–H bond under attack. This point was also confirmed by Ausfelder et al.[11] They used isotope substitution to provide confirmation of the nuclear framework dynamics of this reaction and studied influences on the nascent product OH or OD radicals rotation with fine-structure state partitioning. The absolute rotational energy release is found to be essentially independent of the hydrogen isotope for all observed OH and OD product levels, which indicates a near-collinear abstraction mechanism for this hydrogen-abstraction with the product rotation determined primarily by the geometry at the point of repulsive energy release. As for the other product CH3 radical, the ν2 out-of-plane bending vibrational distribution was determined by Suzuki and Hirota[28] in an infrared diode laser absorption kinetic spectroscopy experiment. Their results suggested that the CH3 moiety was gradually relaxed to a planar structure during these reactions. Laser photolysis of NO2 has been combined with laser-induced fluorescence detection of the nascent OH product to investigate the dynamics of the reactions of O(3P) with methane.[10] The OH spin–orbit (SO) states were found to be nonstatistically populated, which was interpreted by a direct abstraction mechanism with a preferentially collinear C–H–O approach of the O(3P) atom to the C–H bond under attack.
The kinetics of the methane combustion reactions have been studied and the reaction rate coefficients were determined in the temperature range from 298 K to 2500 K. However, it is considerably less reliable due to the uncertainties in the reaction stoichiometry and tunneling effects.[29,30] The experimental data for the reaction was reexamined by Cohen[31] at temperatures below about 600 K. It was found that the values for rate coefficient were overestimated by factors of approximately 2 to 3 in the 250 K–400 K temperature range, with the error increasing as the temperature decreases, and a new expression of the experimental results was proposed as 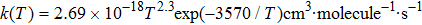
Theoretical studies of this reaction have been carried out using various ab initio and dynamical methods;[1,32–34] however, all studies were based on the reaction channel with only one transition state (TS). The ground PES, constructed by Gonzaleza and coauthors[35] using the PMP4 calculations, was employed to obtain the barrier height of 13.3 kcal/mol for SP1st (3A″). The OHC bending angle is 180.0° and the imaginary frequency is 2259i cm−1. In 2012, high accuracy was achieved by using a high-level electron correlation method to obtain the barrier height of 14.08 kcal/mol and the OHC bending angle of 179.3° at the SP1st (3A″), which was taken as a benchmark value.[34] Later, a new full-dimensional analytical PES-2014[32] for O(3P) + CH4 was accurately constructed based on the CCSD(T) = FULL/aug-cc-pVQZ level, and the barrier height obtained was 14.0 kcal/mol with the corresponding OHC bending angle of 180.0°. The thermal rate coefficients of the reaction were also obtained with ring polymer molecular dynamics (RPMD)[15,36–38] and with variational transition state theory calculations on this new surface.[33] The TST (transition state theory) transmission coefficients were obtained by the least-action tunneling (LAT) approximation. In the classical high-temperature limit regime, the RPMD rate theory result agrees with the experiment perfectly, although it overestimates the experimental rate coefficients in the low-temperature regime;[15,36–38] however, there are still somewhat uncertain aspects in the previous theoretical studies. First, rough estimation of the barrier height extracted from experimental data by Arrhenius plots gives 8.7 kcal/mol to 11.7 kcal/mol,[2,33,39,40] which is much lower than previous theoretical reported values.[32,34,35] Second, since the approach of O(3P) along a C–H bond leads to Jahn–Teller conical intersections,[3,41–45] which are not isolated geometries but form a seam. They are widespread in polyatomic systems and make the SPs more and more elusive, representing a theoretical challenge.[16,17,34,46]
One of the reasons is the inadequacy of a single-configuration reference wave function for the post-Hartree–Fock calculations.[46] The geometries and roles of SPs in the reaction CH4 + O(3P) have not been clarified in previous studies. In order to better understand the reaction mechanism and clarify the role of the SPs, recently our group reported an SP1st (3A″) with the ab initio method and kinetic calculation to obtain a fairly accurate description of the regions around the 3A″ TS in the O(3P) attacking a near-collinear H–CH3 direction with a barrier height of 12.53 kcal/mol,[47] which is lower than those reported before.[32,34,35] Until now, there were few accurate ab initio works about the 3A′ state PES reported due to the existence of a conical intersection, which allows the system to relax to lower electronic states and poses a considerable theoretical challenge.[48–50] To accurately study the combustion reaction 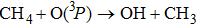
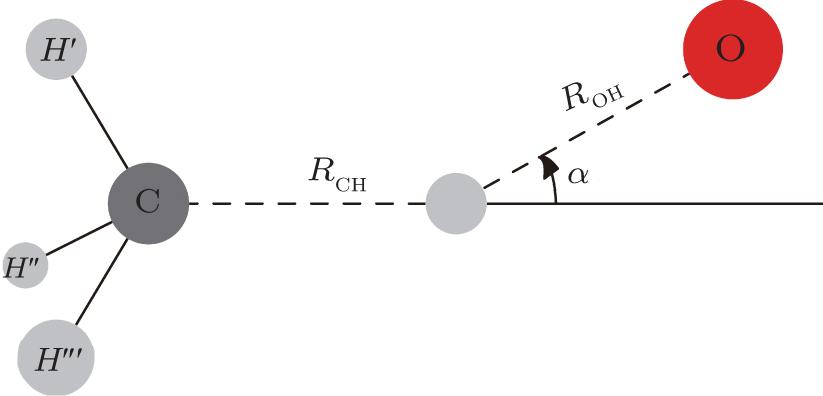
In this work, we present an extensive theoretical study on hydrogen-abstraction reaction of CH4 + O(3P) based upon the accurate ab initio electronic structure calculations, which are performed using the MOLPRO 2008.1 program package.[51] Since the Cs symmetry is the most relevant for all the stationary point geometries (reactants, products, complexes in the entrance and exit channels, and saddle points), for computational convenience, the reaction system is placed in the Cs symmetry and the internal coordinates are employed in most calculations. The coordinates are defined in Fig. 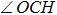

These calculations are based upon the dual-level strategy.[21,52] The details of this computational scheme can be found elsewhere, thus only a brief outline will be given here. As the first step, extensive electronic structure determinations, including the geometry optimizations and vibrational frequencies are performed using the State-Averaged Complete Active Space SCF (SA-CASSCF),[53,54] in which the high level multireference SCF energies and wave functions for a series of ground and excited states are calculated by a state-averaged variational calculation. The selection of the active space is crucial in the CASSCF and icMRCI+Q calculations.[55,56] Here various active spaces in CASSCF calculations have been tested and finally the active space, which consists of twelve orbitals, referred to as (14e, 12o), is chosen for the present calculations. The active space (14e, 12o) is also used for the subsequent icMRCI calculations, and this choice is sufficient to describe the CH bond-breaking and OH bond-forming accurately. It should be noted that the 2s electrons of C and O are put into the closed shell, which means that both 2s orbitals are doubly occupied in all reference configuration state functions, but still are correlated in the icMRCI calculations to account for the core–valence correlations (called CV). The rest of the inner electrons are kept frozen and not correlated. A comparison with the frozen-core and all-electron results for the title reaction have been made, and the result of all-electron is better than that of the frozen-core.[32,34,47,57] The 1s orbitals of carbon and oxygen are not correlated but optimized at the SA-CASSCF level. A reasonable consideration of the basis set dependence is performed. To obtain the CV effects contribution to the energies, especially barriers,[32,58] the cc-pCVDZ basis sets are chosen but modified.[47,59–61]
Since the SA approach included each of the states in question with equal weight and the configuration space is equivalent for all states, SA-CASSCF calculation with 0.5, 0.5 weighting on one root in 3A′ and one in 3A″ symmetries, respectively, is performed using the orbitals obtained with the unrestricted Hartree–Fock method as the starting guess to obtain the orbitals in this work. At the same level, the corresponding frequency calculations of the optimized geometries are also done to prove the characters of minima without imaginary frequencies, the SP1st and SP2nd with only one and two imaginary frequencies, respectively.
The intrinsic reaction coordinate (IRC) calculations are performed by starting from the saddle point geometry at this level in order to identify a given transition state connecting the desired reactant and product.[62] The numerically gradient vector and hessian matrix including rotational partition functions were evaluated at each point along the IRC by harmonic vibrational frequencies calculations. As for the locating of SP2nd, which is also a minimum energy crossing point between 3A′ and 3A″ electronic states, three vectors were evaluated at the SA-CASSCF level: non-adiabatic derivative coupling, gradient of the lower state, and gradient of the upper state.[49,50,63]
In our earlier calculations for the title reaction with SP1st (3A″), only stationary points and each point in the IRC were calculated to evaluate relative energy by using the subsequent icMRCI method, which is for more sophisticated calculations of the single point energy. The calculated potential energy curve (PEC) of ab initio single point energies obtained from higher-level electronic structure calculations might not be as smooth as the counterpart from lower-level IRC calculations, and further rate calculations on the title reaction showed that this does not lead to significant variations of the maximum length of the reaction coordinate. We therefore decided to calculate a few symmetry unique geometries by the icMRCI method in the present work. These geometries were chosen carefully to represent the entrance and exit valley regions most accurately. The icMRCI is a direct MRCI procedure performed in an internally contracted configuration basis, and the MRCI wave functions include all single and double excitations relative to the CASSCF reference functions.[53,54] A large amount of correlation energy is described via single and double electron excitations, and further correlation energy due to higher excitations is approximated by the Davidson correction (+Q).[64] There are at least two reaction channels/transition states (3A′ and 3A″) involved in the title reaction.[25,46] Therefore, two reference states (3A′ and 3A″) are required and used for generating the internally contracted pairs in the icMRCI procedure.
The canonical unified statistical (CUS) theory,[65–67] which considers a complex region between two bottlenecks and does not give a bound even in classical mechanics, and the canonical variational transition-state (CVT) theory is employed in our present work for the kinetic calculations using the general polyatomic rate constants code POLYRATE 2015 program.[68]
The general equation for rate constant calculations in CUS is:
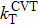
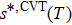
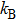
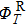

The CUS theory recrossing factor is
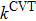
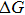
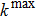
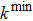
The reaction path is calculated by the Euler steepest-descent method from −5.0 Bohr on the reactant side to +3.0 Bohr on the product side. The rotational partition functions of each point on the reaction path are obtained by ab initio frequency calculations classically, and the vibrational modes are treated as quantum mechanical separable harmonic oscillators, with the generalized normal-modes defined in redundant curvilinear coordinates. The geometries, gradient vector, and Hessian matrix of all points along IRC are obtained from CASSCF, while the energy is obtained from icMRCI +Q. The energy splitting between two electronic states for OH, between 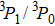
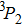
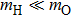
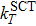
The ground state of the O atom (3P) has the electronic configuration 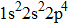

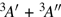

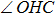
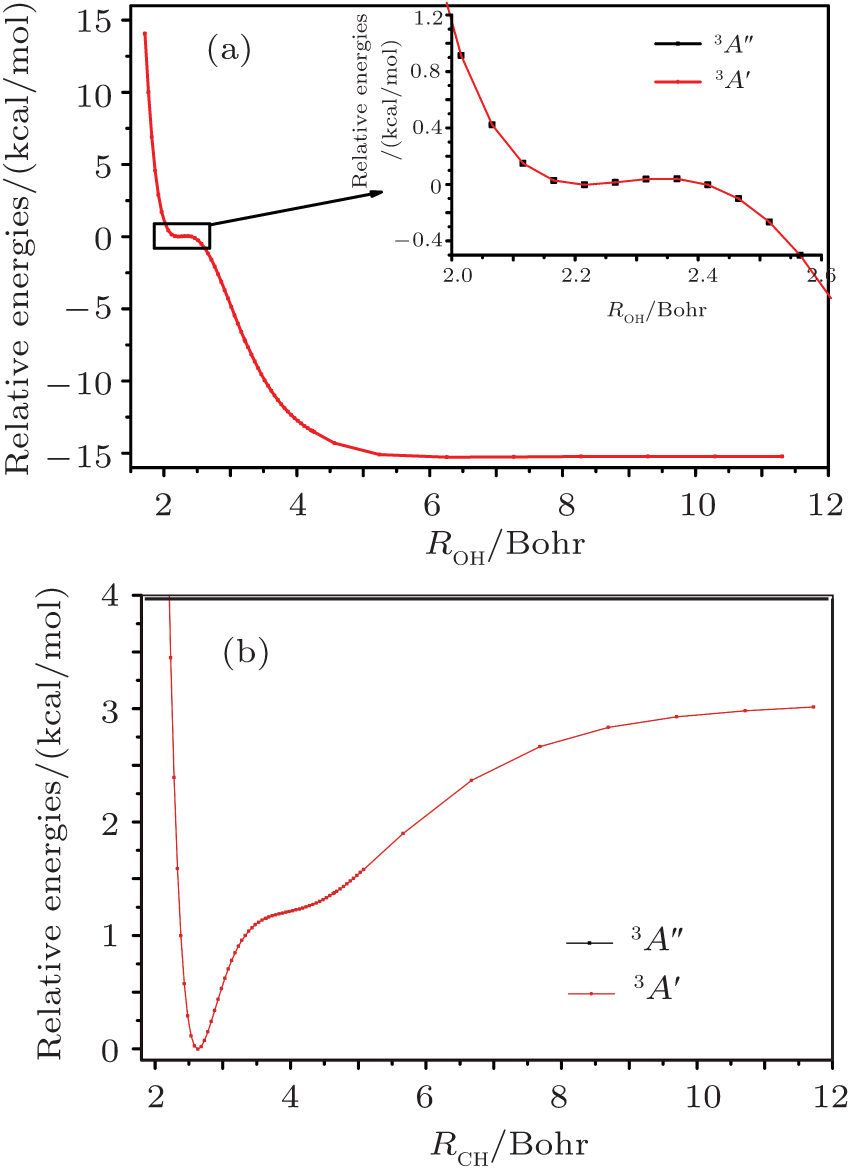
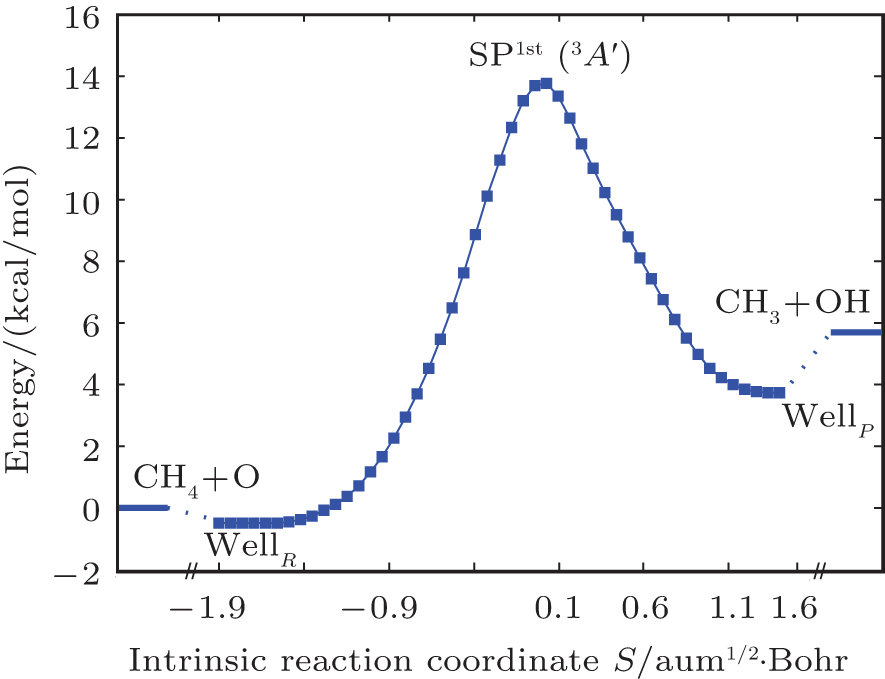
When the distance between C and O is smaller than 9.0 Bohr, the weakly-bound van der Waals (vdW) interaction of the ground-state O atom with methane along the H3C–H–O axis is helpful for orienting the system towards H3CH…O (WellR, 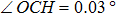
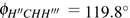
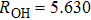
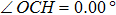
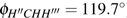
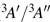
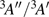
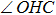
Under Cs symmetry as the O(3P) atom approaches the methane along a C–H bond after WellR, two SP1st are found in the two respective surface of symmetries 3A″ and 3A′ with the length of breaking C–H bonds of 2.644 Bohr and 2.649 Bohr, respectively, and they are almost identical in energy but slightly different in the OHC bending angle and the tilt of the methyl group. The length of the breaking C–H bond in the two Cs symmetry SP1st is about 25.0% longer than the corresponding equilibrium distance in CH4 molecule, while the length of the forming O–H bond in SP1st geometry is about 20.0% longer than the corresponding equilibrium distance of OH. The geometry parameters and the relative energies of SP1st (3A′ and 3A″, respectively) and SP2nd (3E) are listed in the following Table
| Table 1.
Properties of saddle points (SPs) on the reaction path of |
The calculated barriers on both surfaces are around 14 kcal/mol, and the corresponding harmonic vibrational frequencies, performed at CASSCF levels, are 2284i and 2376i[47] in unit cm−1, respectively, for SP1st (3A′) and SP1st (3A″), while the single point calculations at the icMRCI+Q(14e,12o)/optCVDZ level give the barrier heights of 13.28 kcal/mol and 12.53 kcal/mol. The TST calculations in the next rate constant prediction lead to zero-point corrections of 1.46 kcal/mol for the 3A′ state and 1.56 kcal/mol for the 3A″ state. Therefore, including zero-point correction energy reduces the barrier to around 11.07 kcal/mol and 11.72 kcal/mol, respectively. Both 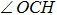
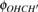
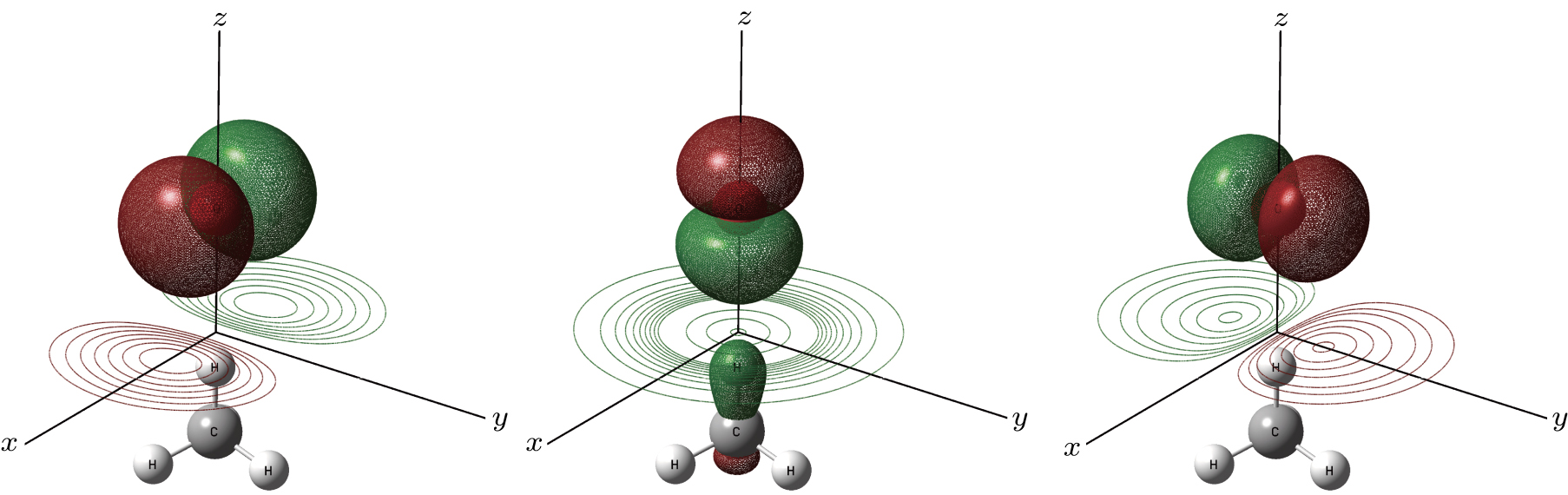
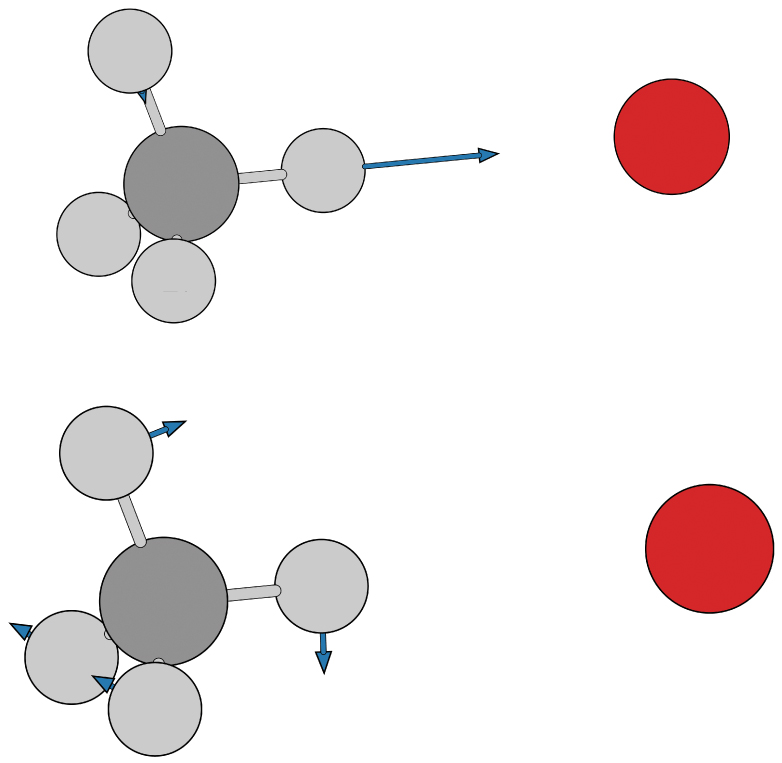
The second order saddle point SP2nd (3E) with linear configuration is found by the optimization of lower-energy points of degeneracy with lower symmetry. This structure presents two imaginary harmonic vibrational frequencies, which are presented in Fig. 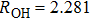
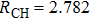
The minimum energy path for SP1st (3A′) is affirmed by an IRC calculation in Fig.
The TST, CVT, and CUS calculations were applied into this reaction with a single saddle point and two potential energy wells. Moreover, these calculations are based upon dual-level strategy extensive electronic structure determinations. The geometries, gradient vector, and Hessian matrix of all points along IRC are obtained from CASSCF, while the energy is obtained from icMRCI+Q//CASSCF(14e,12o)/optCVDZ. The SO coupling calculations for the O(3P) atom and CH4 molecular have been performed using SO pseudopotentials. The obtained energy splitting between two electronic states for OH is 118.2 cm−1, whereas 140.2 cm−1 and 259.9 cm−1 for 
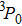
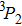
It should be noted that more symmetry unique geometries in the entrance and exit valley regions, calculated with the icMRCI method, were added in the present rate constant calculations of the 3A″ and 3A′ surfaces, respectively. The contribution to the rate from 3A″ and 3A′ surfaces have been calculated separately and summed to give the total rate. In Fig. 
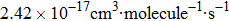
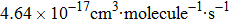
 | Fig. 4. (color online) Arrhenius plot for the reaction of 
|
| Table 2.
Thermal rate coefficients (in unit |
The calculated rate constants of 600 K for the title reaction are 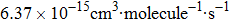

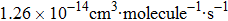
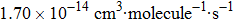
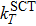
The conventional TST in the present work locates the transition state dividing surface at the SP1st(3A′) and it seems to overestimate the rate constants, presumably due to the neglect of barrier recrossing. Since the harmonic approximation, which leads to an overestimation of the variational effects, is used in the present CUS/CVT calculations, their results could not perfectly match the experimental data at high temperature.[33,38] Our CUS/SCT results are larger at lower temperatures than theirs with CUS/LAT on PES-2014 and smaller at higher temperatures, but both results are in accordance with the available experimental data.
In the present work, we have presented two SPs1st and one SP2nd on an ab initio PES of 
The thermal rate constants for this hydrogen-abstraction reaction are calculated with several dynamical methods including using the canonical unified statistical theory method over a large temperature range. These calculated rate constants of CVT and CUS are in agreement with experimental results; however, TST results are much higher and present noticeable difference in the Arrhenius plots, indicating the important role played by tunneling. The reasonably good agreement with available experimental results confirms the accuracy of our present work. The rate coefficient obtained from CUS/CVT is significantly lower than its previous RPMD result at low temperature below the crossover temperature, suggesting underestimation of the tunneling contribution. It may be attributed to the inaccuracies of CUS and CVT.
This theoretical study will play an important role in shaping our deeper understanding of SPs and bimolecular reactions with polyatomic molecules. Further work on the construction of the global PESs for 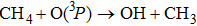
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] |