† Corresponding author. E-mail:
Mutually unbiased bases, mutually unbiased measurements and general symmetric informationally complete measurements are three related concepts in quantum information theory. We investigate multipartite systems using these notions and present some criteria detecting entanglement of arbitrary high dimensional multi-qudit systems and multipartite systems of subsystems with different dimensions. It is proved that these criteria can detect the k-nonseparability (k is even) of multipartite qudit systems and arbitrary high dimensional multipartite systems of m subsystems with different dimensions. We show that they are more efficient and wider of application range than the previous ones. They provide experimental implementation in detecting entanglement without full quantum state tomography.
Quantum entanglement is one of the most intriguing features of quantum mechanics which lies at the heart of quantum information sciences.[1,2] It has wide applications in quantum information processing.[3–12] The separability problem, namely distinguishing separable states from entangled states, is a challenging task whose complexity scales very unfavorably with the size of the system.[13] A possible approach is to consider sufficient criteria for entanglement. For bipartite systems, various separability criteria have been proposed.
When it comes to multipartite systems, the situation becomes much more complicated, because they exhibit a much richer structure than the bipartite case.[13] Although the detection of multipartite entangled states is a harder challenge, it is worthy of study because they have advantages when performing some tasks.[14] Many attempts have been made to frame multipartite entanglement detection, such as witnessing genuine multipartite entanglement,[15–18] detecting k-nonseparable states,[19–22] etc. The main challenge for high-dimensional multipartite systems is not only to develop mathematical tools for entanglement detection, but also to find schemes whose experimental implementation requires minimal effort, that is to say, we need to detect entanglement with as few measurements as possible, specifically independent of full state tomography.
The notion of mutually unbiased bases (MUBs) was first introduced under a different name.[23] Many quantum information protocols depend upon the use of MUBs,[24] such as quantum key distribution, the reconstruction of quantum states, and so on. The concept of MUBs was generalized to mutually unbiased measurements (MUMs)[25] due to the open problem of the maximum number of MUBs for non-prime power dimensions which limits its applications.[26] The construction of a complete set of d + 1 MUMs were found[25] in a finite, d-dimensional Hilbert space, no matter whether d is a prime power. Symmetric informationally complete positive operator-valued measures (SIC-POVMs) is another related topic in quantum information, which has many helpful connections with MUBs, such as operational link,[27] quantum state tomography,[28–30] and uncertainty relations.[31] Since it has some similar limitation as MUBs, in Ref. [32], the authors generalized the concept of SIC-POVMs to general symmetric informationally complete measurements (GSIC-POVMs), which were constructed without requiring to be rank one.
These quantum measurements have been used to detect entanglement recently. In Ref. [33], the authors availed of MUBs and obtained separability criteria in arbitrarily high-dimensional quantum systems. Later some separability criteria for d-dimensional bipartite systems using MUMs were constructed.[34,35] We obtained separability criteria for high dimensional and multipartite systems via MUMs.[36] A separability criterion for d-dimensional bipartite systems using GSIC-POVMs was given in Ref. [37]. Recently, Shen, Li, and Duan proposed three separability criteria for d-dimensional bipartite quantum systems via the MUBs, MUMs, and GSIC-POVMs, which are said to be more powerful than the corresponding ones mentioned above.[38]
The separability criteria mentioned above are of practical significance as they provide experimental implementation in detecting entanglement of unknown quantum states which only depend on some local measurements. What is more, they are an efficient way of characterizing bipartite entangled states. But few of them are referred to entanglement for multipartite systems, which are significant both in theoretical and experimental aspects.
In this paper, we study the separability problem and propose some criteria detecting entanglement for multipartite qudit systems and multipartite systems of different dimensional multi-level subsystems via MUBs, MUMs, and GSIC-POVMs. We show that the criteria in Ref. [38] are the special case of ours for two-qudit systems. In addition, our criteria can be applied to a wider range of multipartite systems and are more efficient than the former ones for multipartite systems. They also provide experimental implementation using only some local measurements.
The details of the notions of MUBs, MUMs, and GSIC-POVMs have been studied in original works.[25,26,32] Here we will briefly review the definitions of these measurements and the notions of k-separability and an operator used in the sequel.
Two orthonormal bases in Hilbert space 



Kalev and Gour generalized the concept of MUBs to mutually unbiased measurements[25] which include the complete set of MUBs as a special case. Two measurements on a d-dimensional Hilbert space,
 |
 |





A set 




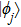



 |



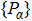
For multipartite systems, there are various kinds of classification for multipartite entanglement. Next we introduce the notion of k-separable state for later use. An N-partite system is described by the following Hilbert space
 |






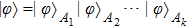


When N is an even number, there are two different classes of bipartite partitions 



 |
 |

 |






In this section, we present three separability criteria using MUBs, MUMs, and GSIC-POVMs. Inspired by the operator (
It is worth noting that Theorem 1 in Ref. [38] is the corollary of Theorem 1. When m=2, 

Next, we present the separability criteria using MUMs and GSIC-POVMs, which are more powerful than that via MUBs due to the fact that the complete set of MUMs and GSIC-POVMs always exist in all finite dimensions.
Note that when the conditions are limited to only two subsystems with the same dimension and the complete sets of MUMs, that is, m = 2, 

 |
When m = 2 and 
For Theorems 1, 2, and 3, the dimensions of subsystems are not required to be the same, so we can straightforwardly detect k-nonseparable states (k is even) with respect to a fixed partition. The sets Sk of all k-separable states with respect to a fixed partition have nested structure, that is, each set is embedded within the next set: 


The criteria given by Theorems 1–3 are much better than the previous ones in Refs. [33,34,37], and Ref. [38]. First, they are more powerful than the main result (inequality (

In recent years, people gradually recognized the significance of multipartite quantum states with higher dimensions. Maximally entangled qudits have been proved to violate local realism more strongly and are less affected by noise than qubits.[43–45] Qudit states also have benefit in quantum communication, since they are more secure against eavesdropping attacks and more reliable in quantum processing.[46,47] From the experimental viewpoint, the entangled qudits can be physically realized in linear photon systems,[48] etc. So it is important to characterize entanglement in multipartite systems, and it is still under intensive research.
In this paper, MUBs, MUMs, and GSIC-POVMs have been used to study the entanglement detection of arbitrary high dimensional multipartite systems. We have presented separability criteria given in Theorems 1–3 to detect entanglement of quantum states in 
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] |

