† Corresponding author. E-mail:
The reversible transfer of unknown quantum states between light and matter is essential for constructing large-scale quantum networks. Over the last decade, various physical systems have been proposed to realize such quantum memory for light. The solid-state quantum memory based on rare-earth-ion-doped solids has the advantages of a reduced setup complexity and high robustness for scalable application. We describe the methods used to spectrally prepare the quantum memory and release the photonic excitation on-demand. We will review the state of the art experiments and discuss the perspective applications of this particular system in both quantum information science and fundamental tests of quantum physics.
The development of quantum information science provides unique techniques and methods to perform many tasks that cannot be achieved by using the conventional schemes based on classical physics. Photons are the natural carriers of quantum information, so optical quantum processing is at the heart of photonic quantum technologies. The storage and retrieval of a quantum state of photons, which is often defined as quantum memory, is an essential ingredient for construction of photonic quantum networks. For instance, quantum memories are the cores of the quantum repeater architectures,[1] which can in principle extend the transmission of quantum information to an arbitrarily long distance. In quantum computation with linear optics, quantum memories can store qubits to maintain synchronization for parallel operations.[2] Indeed, quantum memories may find applications in any assignment that requires the synchronization of several independent and probabilistic events such as creation of deterministic photons through a probabilistic single photon source.
Optical quantum memory has attracted the interest of many groups in the world because of its great prospects. Different media systems have been employed to implement quantum memory, such as atomic ensembles,[3] single atoms,[4] and solid-state crystals.[5] Research of light and its interaction with different systems promotes the research in other disciplines, such as material science, atomic spectroscopy, electron and nuclear spin manipulations. Therefore, quantum memory also provides a link to explore some fundamental tests of quantum physics. Resent years have seen significant progress in quantum memory research, including the extension of the storage time, enhancement of capacity and attempts to build a simple quantum network based on quantum memories; Refs. [6–8] for a review. The solid-state quantum memories are proven to have the longest coherence time. Meanwhile, the simplifying setup makes them robust and scalable. These characteristics lead them to be promising and outstanding candidates for the practical construction of quantum networks. Due to the rapid progress in the field of solid-state quantum memory, particularly over the past decade, we endeavor to track a report of the most recent advances in this field.
The article is organized as follows. In Section
In addition to the long optical[9] and hyperfine coherence time,[10–12] the rare-earth-ion-doped crystals (REICs) also benefit from the large inhomogeneous broadening[13,14] of the optical transition. However, the inhomogeneous broadening also results in the rapid decay of the atomic coherence after photon absorption. Therefore, most memory protocols are dedicated to solve the dephasing problem in the REICs. Commonly used protocols include the electromagnetically induced transparency (EIT),[15] controlled and reversible inhomogeneous broadening (CRIB),[16,17] atomic frequency comb (AFC),[18] and the embedded quantum memory originating from the DLCZ protocol.[19,20] It is worth noting that to date, none of the protocols with a specific medium has shown the best performance for all desired indicators; therefore, a suitable memory protocol should be chosen considering the specific requirements of the application.
For example, as the primary impetus of the quantum memory research, most quantum repeater protocols require a long-term on-demand quantum memory,[21,22] but this does not mean that memories based on two-level AFC protocol are useless in this field. In 2014, Tittle’s group proved that it is possible to employ quantum memories with spectral multiplexing and fixed storage times to complete the quantum repeater task.[23] Their main idea was to use many modes in the frequency domain or other degrees of freedom (DOFs)[24] to ensure a near-unity probability of a successful Bell-state-measurement (BSM) at the central elementary links, supplemented by mode conversion and feedforward control. This protocol can significantly accelerate the entanglement distribution rate compared to the direct transmission of single photons, so these quantum memories with predetermined storage time can also be used to construct quantum communication channels. Furthermore, the two-level AFC protocol may find applications in tasks such as quantum computing because of their low noise ratio, which lead to a high write-read fidelity.
In 2008, Gisin’s group achieved the goal of storing the weak coherent pulses at the single photon level (SPL) in the Nd3+:YVO4 crystal by using the AFC protocol.[25] This protocol is based on shaping an inhomogeneously broadened optical transition |g〉 → |e〉 into a periodic series of narrow and highly absorbing peaks with periodicity Δ, where an additional ground state |aux〉 is used as the population storage reservoir. After the bandwidth-matched photon is absorbed by the atomic frequency comb, the collective atomic state has the following form:[18]
Two years later, Lauritzen et al. reported the storage of telecommunication-wavelength light at SPL in an erbium-doped crystal by using the CRIB protocol.[26] This protocol is based on controlling the inhomogeneous broadening by applying the electric field. A narrow absorption line is prepared by spectral hole burning technologies and is then broadened by the external electric field because of the Stack effect. The spectral width of the broadened line should match the bandwidth of the photon to be stored. After the signal photons are absorbed (t = 0) by the broadened line, the atoms that have detuning δ with respect to the central frequency gradually accumulate phase exp(−iδτ) at the time t = τ. A polarity inversion of the electric field is applied at this moment and therefore the atoms invert their detuning later. At time t = 2τ, atoms have accumulated the opposite phase exp(iδτ) which leads to collective rephasing and the photon is re-emitted. When the electric field varies longitudinally along the propagation of the signal photons, a modified CRIB protocol is proposed as gradient echo memory (GEM).[27,28]
Following the pioneering works on storing quantum light with low efficiencies, many experimental studies have been performed seeking a higher storage efficiency.[29–31] An impressive 69% storage efficiency was realized at a storage time of 1.3 μs in the Pr3+:Y2SiO5 crystal using the GEM protocol.[31] The longitudinally varying electric field avoids the re-absorption of the re-emitted photon to achieve a high efficiency. The storage efficiency of the AFC protocol can also be enhanced by using an impedance matched cavity.[32] This was demonstrated by Sabooni et al. in 2013.[33] They used a cavity-enhanced AFC protocol in a Pr3+:Y2SiO5 crystal with weak absorption and obtained an efficiency of 56%.
Multiplexed operation of the quantum memory can significantly enhance the data rate in quantum-repeater-based quantum channels.[21–23] In REICs, the temporal multimode capacity is always related to the value of the storage bandwidth. In 2010, the coherent and reversible mapping of 64 temporal modes to the solid-state ensemble of rare-earth ions was reported with a 100-MHz AFC.[34] Laboratoire et al. improved this value to 1064 classical laser pulses with a 0.93-GHz storage bandwidth,[35] also employing the AFC protocol. Multiplexing in the frequency domain has also been demonstrated with at least 26 spectral modes stored in the Ti:Tm:LiNbO3 waveguide supplemented with frequency-selective recall.[23]
Compared to the temporal and frequency modes, quantum information always favors being encoded in the polarization DOF which has stronger anti-disturbance against the environment. This has motivated the research of storing the polarization qubits in the REICs. In 2012, three different groups, including ours, reported polarization qubit storage experiments. We used two crystals sandwiching a half wave plate (HWP) to store the photons with arbitrary polarizations.[36] The compact design of the memory hardware reduced the complexity of the memory setup and improved the stability compared to the device presented in Refs. [37] and [38], thereby a process fidelity of 99.9% was achieved. This is the highest fidelity ever achieved for the storage of polarization qubits, which makes it ultra reliable for quantum error-correction applications in large-scale quantum computation.
In 2015, our group conducted the first experiment of storing the three-dimensional (3D) orbital angular momentum (OAM) in the REIC, accompanied by a certification of the high spatial-multimode capacity of the solid-state system.[39] The OAM entanglement source is generated by a spontaneous parametric down conversion (SPDC) process, which is naturally entangled in the DOF of OAM with a convenient setup. However, the spectral bandwidth of the state is much larger than the bandwidth of the storage device. Two efforts were made to solve this problem. First, two etalons were introduced into the entanglement source to limit the bandwidth of the source to approximate 700 MHz. Then we used acousto–optic modulators (AOMs) and two electro–optic modulators (EOMs) to program the preparation of the AFC, which increase the storage bandwidth to approximately 1 GHz.
As shown in Fig.
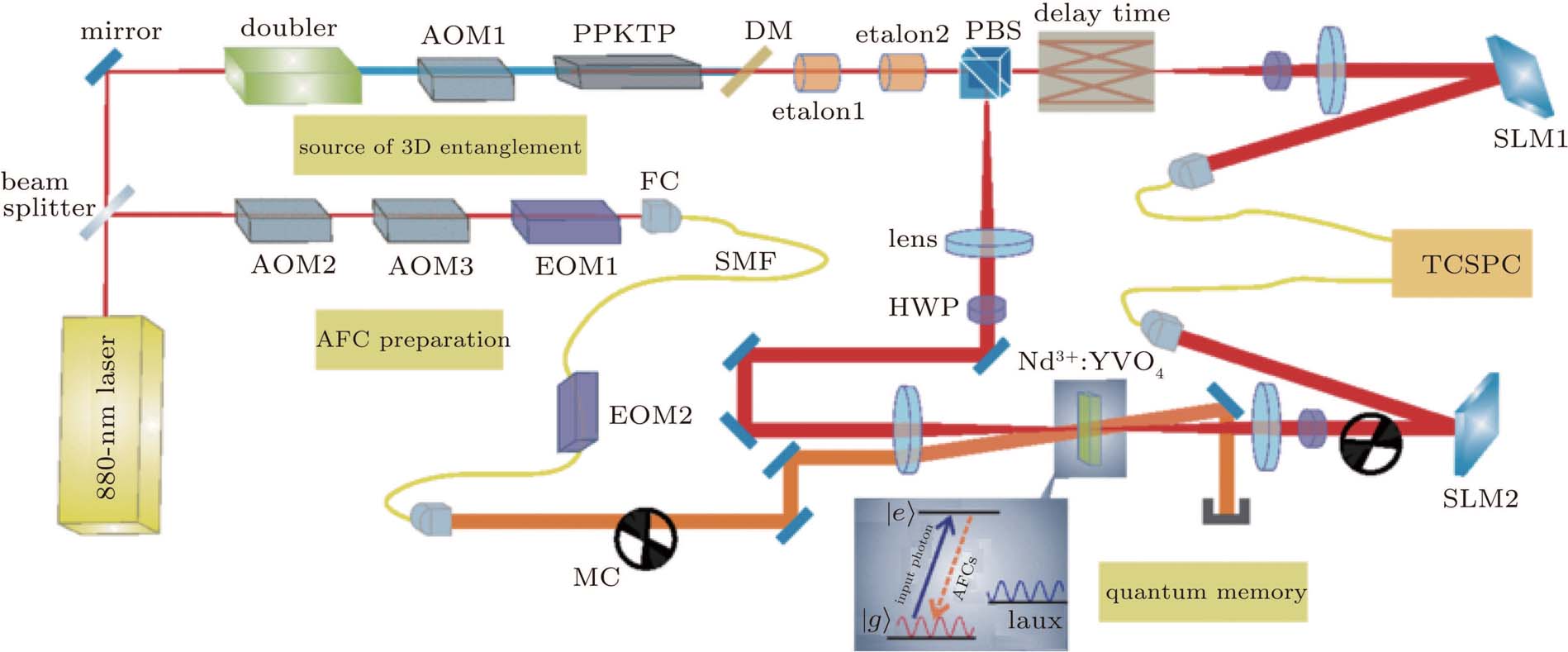 | Fig. 1. (color online) Diagram of the experiment of storage three-dimensional entanglement. The photon pairs were generated in the 20-mm PPKTP crystal via spontaneous parametric down-conversion (SPDC). The photon-pair source was spectrally filtered by the two etalons to match the bandwidth of the memory crystal and separated by the polarized beam splitter (PBS). The signal photons were stored in the Nd3+:YVO4 crystal using the AFC protocol. The OAM state of the signal and idler photons are analyzed by two spatial light modulators (SLMs). The phase-locked mechanical choppers (MCs) were used to protect the single-photon detector (SPD) during the AFC preparation procedure (from Ref. [39]). |
The high dimensionality and spatial-multimode capacity of the memory were also explored. Weakly coherent pulses were modulated by an SLM to have superposition states in high-dimensional spaces before the memory device. The retrieved photon states from the memory were analyzed by using another SLM. To completely characterize the memory performance in three dimensions, we performed quantum process tomography for qutrit operations. The fidelity before and after the memory is 0.993 ± 0.002, proving the memory itself is ideal. The visibility of the superposition states was used to assess the memory performance for states in higher-dimensional spaces. The visibility of the stored states exceeded 0.95 for a |l ≤ 25|, demonstrating the high reliability of the memory for the total of 51 spatial modes. For the future applications in quantum repeaters, the temporal modes and spectral modes are all limited by the AFC bandwidth, but the spatial multimode capacity in the DOF of OAM shows no dependence on the AFC bandwidth.
Indeed, the different DOFs of photons are often independent, so it is possible to involve multiple DOFs of photons as quantum information carriers, which will greatly enhance the capacity of quantum memory and lead to a low storage time requirement in the quantum repeater framework. There have been several attempts to create this type of versatile quantum memory. Saglamyurek et al. showed essentially arbitrary spectral and temporal manipulations in the wide-band Tm:LiNbO3 waveguide.[41] By dividing the absorption area to several AFCs with different tooth spacing, they demonstrated sequencing, time-to-frequency multiplexing and demultiplexing, splitting, interfering, temporal and spectral filtering, compressing and stretching as well as on-demand selective delaying by using this quantum memory. Two years later, erbium-doped optical fiber was used to perform a spectral-temporal manipulation of a heralded photon with an ultra-wide bandwidth.[42] Multiplexed quantum memories of time-bin and polarization qubits was also characterized in 2016 by Gisin’s group.[43] Recently, our group demonstrated the first quantum memory that can be multiplexed in time, frequency and spatial domain simultaneously (manuscript in preparation).
Storing a single photon is the basic and fundamental step towards elementary quantum networks based on quantum memory. The single photon sources can be split into the heralded and deterministic single photon types. Storing the herald single photons created via SPDC.[37,44,45] has already been realized by many groups. Further, we demonstrated the mapping of a deterministic photon source to a solid-state system. In 2015, we realized a solid-state quantum memory of the deterministic photons emitted from the semiconductor self-assembled quantum dot (QD)[46] for the first time. The single photon source from QD completely eliminates the multiphotons in principle. Moreover, the enhanced photon emission rate can greatly accelerate the data rate of quantum repeaters.[22] The main challenge is the wavelength matching of the two independent systems. The memory crystal is Nd3+:YVO4 crystal which has an optical transition at 879.7 nm, while the emission lines of InAs/GaAs QDs are random, depending on the chemical composition and the dot size in a wide range of approximately 900 nm–1200 nm. Methods including QD sample fabrication, QD selection and local heating of the selected QD were employed to move the emission line of QD to the storage window of the memory crystal. The experimental setup is shown in Fig.
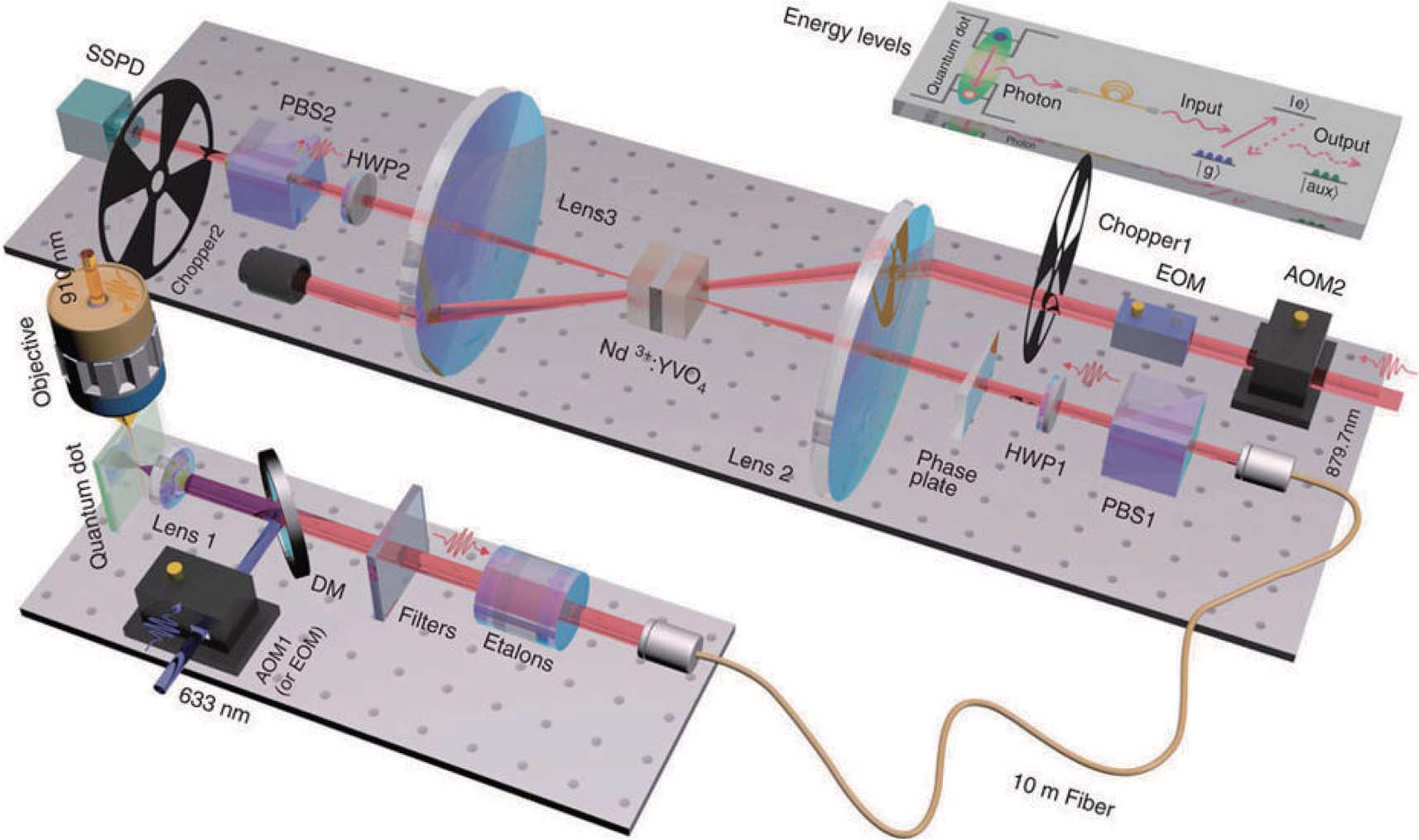 | Fig. 2. (color online) The experimental setup of storing deterministic single photons emitted from a quantum dot in a solid-state crystal. Two separated optical tables were used for generation of single photons and quantum memory separately, which were connected by a 10-m fiber (from Ref. [46]). |
Storage of photonic entanglement is an important part of the effort toward the implementation a quantum repeater, which supports the entanglement distribution and quantum cryptography. In 2011, storage of energy–time entanglement[48] and time–bin entanglement[49] were both realized with an Nd3+:YVO4 crystal and an erbium-doped fiber. The entanglements were both generated by the SPDC process and were stored reliably, as proved by the violation of the Clauser–Horne–Shimony–Holt (CHSH) inequality[50] using the Franson-type set-up.[51] In the waveguide quantum memory, the bandwidth of the memory device has been increased in recent years,[41,52] thus providing a promising method for multiplexing in the frequency domain. The experimental verification of the heralded entanglement between two independent quantum memories in the solid-state system was also completed in 2012.[53] Entanglement between two memory crystals was realized by coherently storing a photon (signal) in two crystals, which is heralded by another photon (idler) from SPDC. The impressive process also includes quantum teleportation from a telecom-wavelength photon to a solid-state quantum memory[54] and storing hyperentanglement[55] in the rare-earth-ion-doped solids. All of these works have advanced the research of the construction of an elementary quantum network based on quantum memories.
To obtain a long storage time using the REICs, a long-lived collective spin excitation (or the spin-wave storage) should be utilized. In fact, both the CRIB and the AFC protocols show the capacity of spin wave storage. The main challenge is the signal-to-noise ratio (SNR), especially for the storing signal at SPL. To transfer the optical excitation to the long-lived spin excitation, a strong control field is needed. However, the spectral separation between the signal field and the control field is much closer in REICs than that of alkali atomic systems which have already been used in spin-wave storage. Scattering from the control field is thus more likely as it propagates through a dense solid-state crystal, which greatly decreases the SNR.
We introduce the spin-wave storage by using the AFC protocol as an example, which is often defined as the full AFC protocol.[18] As shown in Fig.
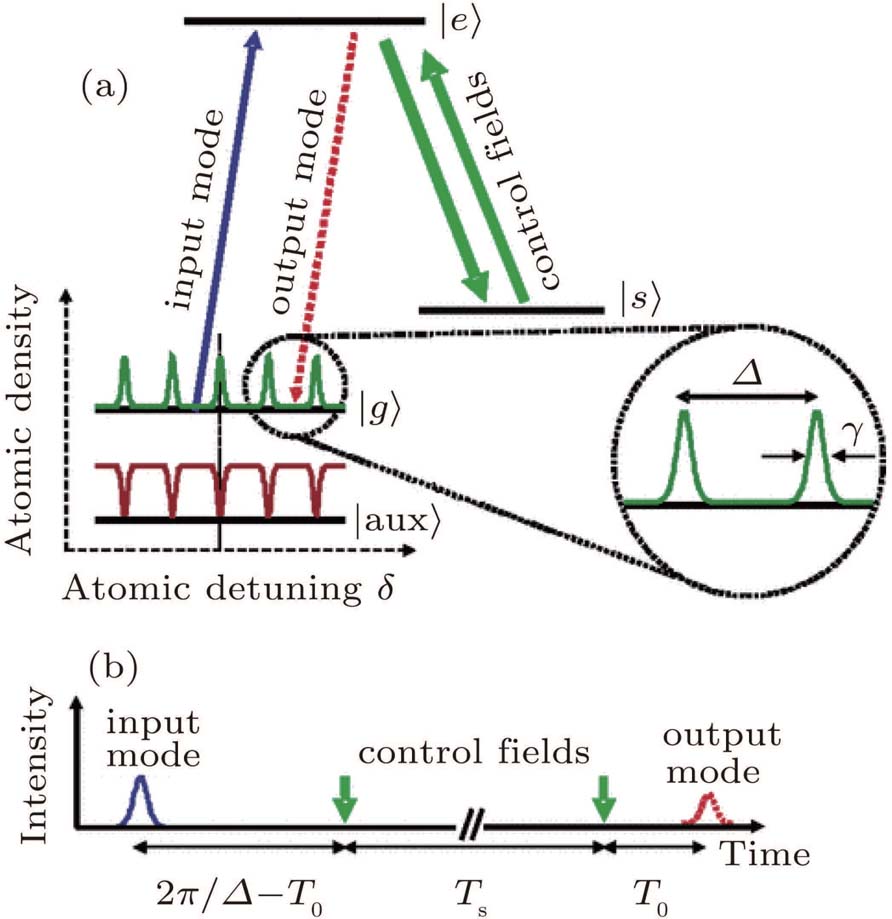 | Fig. 3. (color online) The principles of the full AFC protocol. (a) The required energy levels of the protocol. (b) The sequence diagram of the full AFC protocol (from Ref. [18]) |
Only a few studies investigated the spin-wave storage[57,58] before 2013 and all of these works used bright classical pulses. In 2013, the first spin-wave storage experiment with a signal at SPL was achieved in the 151Eu3+:Y2SiO5 crystal.[59] To suppress the noise caused by the control fields, the spatial and temporal separation of the control field and the signal pulse was applied, but the suppression was not sufficient. They further used the diffraction grating and a Fabry Perot (FP) cavity to spectrally filter the noise. The memory crystal can also be used as a spectral filter using the hole burning techniques.[60] In 2015, Riedmatten’s group used a second memory crystal as a filter and successfully stored the time–bin qubits with the full AFC protocol in a Pr3+:Y2SiO5 crystal, which has an SNR over 10 for the signal at SPL.[61] The efficiency of spin-wave storage was also improved in recent years. By applying a low fineness but impedance matched cavity,[62] a two-level AFC storage efficiency of 53% and the spin-wave storage efficiency of 12% were achieved using a 153Eu3+:Y2SiO5 crystal. In 2016, a 31% spin-wave storage efficiency was achieved using the spectral-hole memory at SPL.[63] The protocol is also based on the slow light effect, but its excellent SNR and ability to work at quantum regime make it promising for use in long-lived quantum storage. The spin transfer efficiency can be further enhanced by chirped adiabatic control fields.[64] The two-level storage efficiency can also be improved by designing the absorption line shape in the atomic frequency comb[65] such that a high retrieval efficiency can be expected. We should point out that the most efficient memory with an on-demand retrieval using REICs was completed by the EIT protocol,[66] but the strong noise makes the protocol unsuitable for storing quantum light.
Demonstration of the capacity to store single photons is another challenge. Since the spin states separation is small, the spin-wave storage bandwidth is just several megahertz which make it difficult to obtain a good SNR. Similar to the two-level storage experiment, it is easy to consider the single photon from SPDC, but the natural bandwidths of the sources are four or five orders of magnitude larger than the required memory bandwidth. Cavity-enhanced SPDC is a solution for obtaining a source with a bandwidth of several MHz. By placing the nonlinear crystal into a cavity, the probability of generating resonant photon pairs is enhanced and the bandwidth is simultaneously restricted. The experiment of the cavity-enhanced SPDC was reported in 2013,[67] with the signal photons at the absorption window of the Pr3+:Y2SiO5 crystal and idler photons at the telecommunication window of fibers. The bandwidth of the source is approximately 2 MHz. Then, the two-level storage of the source was realized in 2014 by using the AFC protocol.[68] By improving both the quality of the source and the memory performance, mapping of the correlated single photon onto a spin collective excitation has just been reported this year by the same group.[69] Not long ago, they reported a source of frequency-bin entanglement using the same cavity-enhanced SPDC setup,[70] in which the frequency bins are separated by approximately 500 MHz. The storage of the source remains difficult because several AFCs must be prepared and the spin transitions of all optical excitations must be applied simultaneously.
The experiments mentioned above are all read-write quantum memory which means that the external quantum sources of light are mapped in the quantum memory. The external source should be generated with the required bandwidth that matches the quantum memory. In practice, it is possible to combine the single photon source with the storage media in a single system. The scheme was proposed by Duan, Lukin, Cirac, and Zoller (DLCZ) for creating long-lived, long-distance entanglement between atomic ensembles.[19] It is based on the creation of a single collective spin excitation (spin-wave) by spontaneous Raman scattering, heralded by a Stokes photon. The excitation can then be retrieved to the anti-Stokes photon by a resonant read control pulse. The single photon source generated by the DLCZ protocol is similar to the source via SPDC in many ways, especially in the aspect of a Stokes photon heralding a single anti-Stokes photon. The main difference is that heralded atomic excitation is long-lived and can be retrieved at a long time. This characteristic makes the protocol suitable for the implementation of a quantum repeater. It has made impressive progress in the atom system, including long duration and efficient retrieval of a collective atomic excitation,[71,72] entanglement with two remote ensembles,[73] and demonstration of entanglement swapping between two pairs of nodes.[74] Recently, a quantum secure direct communication[75] was realized by employing this type of inherent quantum memory.[76]
The conventional DLCZ scheme is always in a temporally single mode, which makes it have a low capacity of carrying quantum information. REICs have the required Λ energy levels. Moreover, due to their wide inhomogeneous broadening, it appears that temporal multimodes can be introduced in this scheme. However, the weak oscillator strengths are the drawback of the REICs, which make the off-resonant Raman scattering difficult. Using the resonant excitation will introduce the rapid inhomogeneous dephasing of the generated collective spin excitation, resulting in a low readout efficiency of the anti-Stokes photons. It is natural to consider using the same methods mentioned above to overcome the dephasing problem, for instance, tailoring the absorption line as an AFC.[20] This was first proposed in 2011, but it was just this year that two groups performed experimental verifications, in which they proved the non-classical correlation between photons and spins in REICs.[77,78] The crystals that they used were the Pr3+:Y2SiO5 crystal and the 151Eu3+:Y2SiO5 crystal, respectively. Both of these studies showed that the AFC-based DLCZ protocol has the capacity of storing the multiple temporal modes. We should mention that another embedded quantum memory protocol of the rephased amplified spontaneous emission (RASE) has proven the ability to carry the non-classical correlation between the ASE field and the RASE field accompanied by a spin-wave storage,[79,80] which inherently supports temporal multimodes. Earlier in 2016, Sellar’s group experimentally verified this protocol in the Pr3+:Y2SiO5 crystal, in which quantum correlations were demonstrated in the continuous variable regime using heterodyne detection techniques.[81]
Although the spin population time T1 in the REICs is long, e.g., T1 ∼ 100 s in Pr3+:Y2SiO5,[56,82] stochastic magnetic interactions between the dopant ions and the host matrix lead to a reduced coherence time (T2) of the spin state. For instance, the nuclear coherence time of the Pr3+:Y2SiO5 crystal is approximately 500 μs, which limits the total storage time to the order of μs. There are several possibilities for increasing the spin coherence time by an external magnetic field and dynamic decoupling (DD).[10,11] The first method is called the zero first-order Zeeman shift (ZEFOZ) technique, in which the specific 3D magnetic field makes the chosen spin transition insensitive to the perturbations induced by the host matrix. The dynamic decoupling is analogous to the photon echo technique mentioned above but for spin transition. The applied ratio-frequency pulses can theoretically rephase all the spin decoherence, thereby making T2 close to T1. Usually, the two methods are coordinated with each other to enhance the spin coherence time to a considerable value.
Choosing the ZEFOZ magnetic field and the spin specific transition is a challenging and complex work, so we briefly introduce the methods to provide a better understanding of the process. First of all, the effective spin Hamiltonian of a non-Kramers ion inside a single crystal is[83]
In 2004, Fraval et al. proposed the method of extending the hyperfine coherence time in the Pr3+:Y2SiO5 crystal by applying a static magnetic field.[10] They have achieved the phase memory time of 82 ms in the specific spin transition. Then, through combination of the dynamic decoupling sequences with the critical point of the magnetic field, a 30-s spin coherence time was realized.[11] Experiments have also been conducted in other crystals, such as Tm3+:YAG[85] and Pr3+:La2(WO4)3 crystals.[86] Both of these obtained an enhancement of the hyperfine coherence time to several hundred milliseconds. A long coherence time of more than one second was also realized in the 167Er3+:Y2SiO5 which has an optical transition near the telecommunication window.[87] This was achieved by applying a sufficiently large magnetic field to suppress the electron spin flip. This crystal enables a suitable candidate for spin-wave storage at telecommunication wavelengths. The first long-duration optical memory with dynamic decoupling in REIC was reported in 2005.[88] The Pr3+:Y2SiO5 crystal was used to store the coherent pulse with the storage time of greater than one second. Storing light with a high fidelity using DD was realized in 2013 using the Pr3+:La2(WO4)3.[89] Storage of the image for a time of one minute was also reported using the Pr3+:Y2SiO5 crystal in 2013. In this experiment, optimization of the ZEFOZ field and optimization of the preparation were implemented by a self-learning evolutionary strategy.[90]
In fact, nuclear spin states of Eu3+:Y2SiO5 are particularly attractive for the spin-wave storage and manipulation due to their extremely long observed lifetime of 23 days.[91] The spin coherence characteristics of the Eu-doped crystal were studied by Sellars’s group in 2006.[83] In 2016, they reported a nuclear spin coherence time of six hours.[84] This extraordinary coherence time was achieved by optimally choosing a large ZEFOZ magnetic field combined with dynamic decoupling.[84] The “frozen core” effect[92] that is beneficial for a long coherence time at the existence of a strong magnetic field was also observed. The preservation of quantum coherence of an hour-long timescale is a remarkable result for the development of quantum information science. Further research into the storage and retrieval of optical signals using the spin-wave technology may make the remote entanglement distribution easier.[93,94] Instead of using the quantum repeater architecture, the task could be simplified by the generation of entanglement and physically transport the memory device. The key point in this scheme is to maintain a stable magnetic field during transport. Although this new scheme has less complexity of the instrument, it shows the better performance in the aspect of transmission losses compared with the fiber transmission at the distance of hundreds of kilometers, which will find applications in quantum communication and tests of quantum mechanics.
Probing the foundations of quantum mechanics has been a long-standing goal because quantum mechanics predicts microscopic phenomena with undeniable success. Quantum memories, which connect the quantum optics and the matter system, provide a powerful method to test some fundamental questions.[45,95–98] For instance, light-matter entanglement through a quantum memory with an approximate unity efficiency followed by Bell state measurement can offer a promising approach to close detection and locality loopholes in the tests of Bell inequality.[99] In addition to the Bell inequality focus on the local realism, the question of the location of the boundary between the quantum and classical domains is of wide importance, in which the scale of involved particles is considered. In other words, whether quantum superposition and entanglement can exist in macroscopic systems is at the heart of the question.[100]
Leggett–Garg-type inequalities (LGtI)[101,102] aimed at providing a quantitative criteria for characterizing the boundary. In 2015, our group presented the first experiment violation of the LGtI using quantum memory in an REIC.[45] Instead of using the assumption of noninvasive measurements[103] or ideal negative measurements,[104,105] the assumption of stationarity[106–108] was used which can be tested experimentally. When stationarity holds, LG-like inequalities can then be formulated as follows:
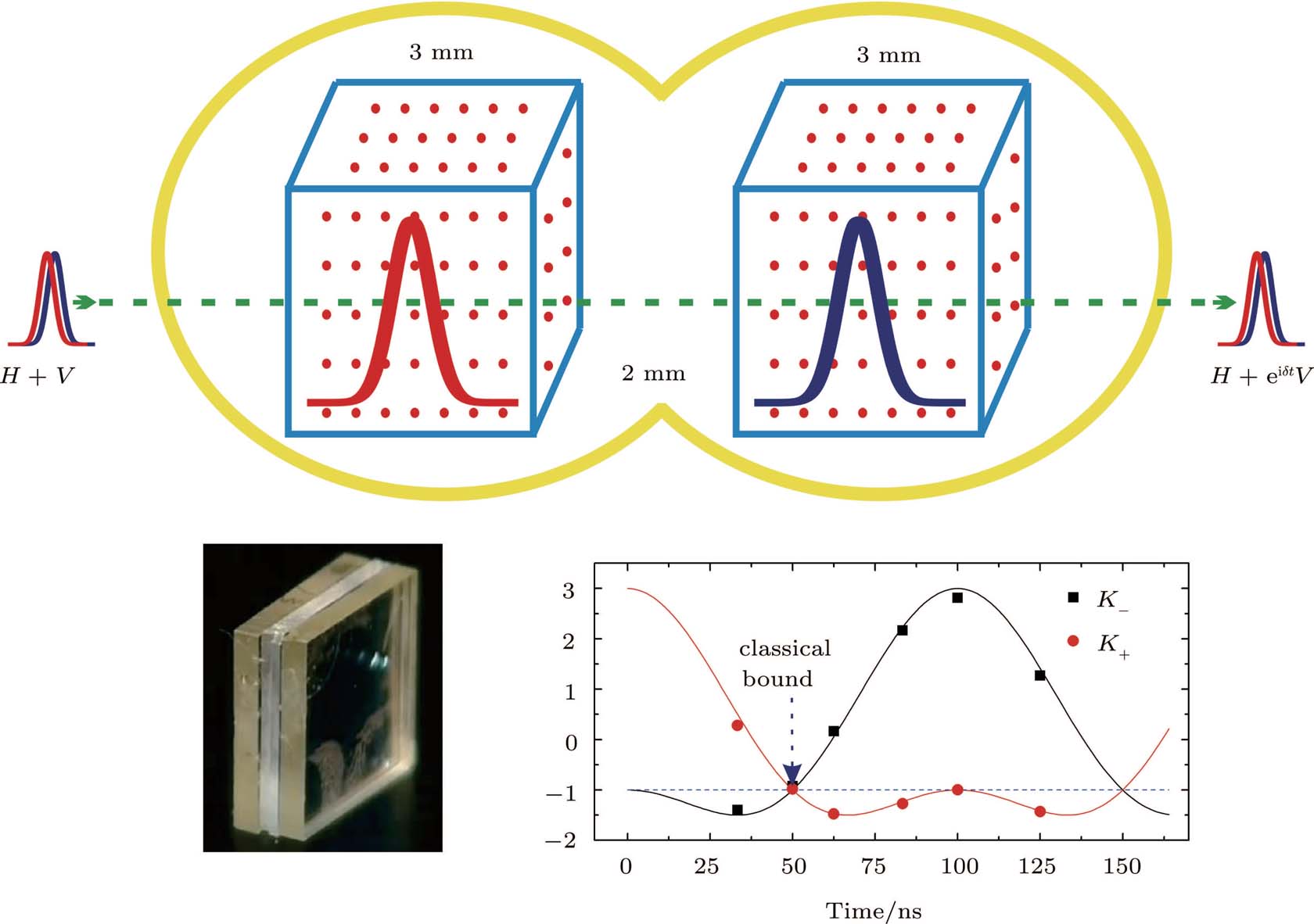
The experimental violation of LGtI was tested by the generation and probing delocalized atomic excitation over the two macroscopically separated crystals. The two pieces of Nd3+:YVO4 crystals sandwiching an HWP were used to store a herald single photon generated via SPDC with arbitrary polarization. Two crystals ware prepared of two AFCs with the same periodicity Δ, but a frequency detuning δ was set between the AFCs. The appropriate polarization states of the single photons were chosen before the memory crystals and the photons were then absorbed by two crystals. This lead to the evolution of the atomic excitation of the two ensembles.
The assumption of the stationarity and the violation of the LGtI were examined independently. The stationarity was verified from the time translation invariance of the system evolution with memory, completed by Markovian behavior of the evolution without the memory effects.[108] Choosing the dichotomic observable M(t), a violation of the LGtI was found. The evolution of K− and K+ are shown in Fig.
Although the quantum state involved two delocalized excitations over a millimeter scale in the experiment, the considered states are of low disconnectivity (D = 1)[109] and can only be treated as a microscopic excitation in macroscopic objects. There are also experimental works that aim at improving the macroscopicity. Last year, Tiranov et al. reported the demonstration of light–matter micro–macro quantum correlation.[95] They used dozens of atomic excitations and the quantum correlation was verified by the Clauser–Horne–Shimony–Holt (CHSH) Bell inequality and quantum state tomography. Earlier in this year, Zarkeshian et al. found substantial entanglement among more than two hundred atomic ensembles in a solid.[96] They also created a multi-particle entangled state by storing a single photon in the wide-band AFC, in which the lower bound of the number of entangled ensembles was derived. All of these works promote the research of exploration of the boundary between the classical world and the quantum world.
To conclude, we have reviewed several recent advances in the solid-state quantum memory, as well as some typical applications in fundamental tests of quantum physics by using REICs. It is worth noting that there are other useful techniques that may further improve the performance of the quantum memories, such as the growth of high-quality crystals,[110,111] studies of spectroscopic properties[112–114] of rare-earth ions in optical crystals and research of integrated photonic memories.[115] Moreover, many other new memory protocols[116,117] are proposed which may have distinctive advantages in REICs. However, so far, excellent performances have been obtained by using different media and different protocols. Challenges remain to be solved to combine these benchmarks into a single and simple media for practical use. We note that the specific quantum information processing tasks can also provide a less strict requirements of the quantum memories by using special designs of some protocols such that existing quantum memories may find applications. For example, a semihierarchical quantum repeaters protocol will reduce the requirement of the storage time to a moderate value of tens of milliseconds.[118] By employing the robust and ease-of-use solid-state quantum memories in these novel protocols of quantum information processing, the construction of memory-based quantum networks is no longer a theoretical wonder.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] | |
| [60] | |
| [61] | |
| [62] | |
| [63] | |
| [64] | |
| [65] | |
| [66] | |
| [67] | |
| [68] | |
| [69] | |
| [70] | |
| [71] | |
| [72] | |
| [73] | |
| [74] | |
| [75] | |
| [76] | |
| [77] | |
| [78] | |
| [79] | |
| [80] | |
| [81] | |
| [82] | |
| [83] | |
| [84] | |
| [85] | |
| [86] | |
| [87] | |
| [88] | |
| [89] | |
| [90] | |
| [91] | |
| [92] | |
| [93] | |
| [94] | |
| [95] | |
| [96] | |
| [97] | |
| [98] | |
| [99] | |
| [100] | |
| [101] | |
| [102] | |
| [103] | |
| [104] | |
| [105] | |
| [106] | |
| [107] | |
| [108] | |
| [109] | |
| [110] | |
| [111] | |
| [112] | |
| [113] | |
| [114] | |
| [115] | |
| [116] | |
| [117] | |
| [118] |