† Corresponding author. E-mail:
We propose an arbitrated quantum signature (AQS) scheme with continuous variable (CV) squeezed vacuum states, which requires three parties, i.e., the signer Alice, the verifier Bob and the arbitrator Charlie trusted by Alice and Bob, and three phases consisting of the initial phase, the signature phase and the verification phase. We evaluate and compare the original state and the teleported state by using the fidelity and the beam splitter (BS) strategy. The security is ensured by the CV-based quantum key distribution (CV-QKD) and quantum teleportation of squeezed states. Security analyses show that the generated signature can be neither disavowed by the signer and the receiver nor counterfeited by anyone with the shared keys. Furthermore, the scheme can also detect other manners of potential attack although they may be successful. Also, the integrality and authenticity of the transmitted messages can be guaranteed. Compared to the signature scheme of CV-based coherent states, our scheme has better encoding efficiency and performance. It is a potential high-speed quantum signature scheme with high repetition rate and detection efficiency which can be achieved by using the standard off-the-shelf components when compared to the discrete-variable (DV) quantum signature scheme.
A quantum signature is the development or extension of a digital signature. In classical cryptography schemes, the digital signature has a great importance by guaranteeing the proof of the source and the integrity and authenticity of messages. Accordingly, digital signatures have been applied in a wide variety of fields, for example, electronic government affairs, electronic medical and electronic payment. Its security is based on computational complexity. Nevertheless, in theory, any cryptography scheme on account of computational complexity can be compromised. The well-known RSA public key cryptography system has been proven to be quickly cracked via future quantum computers,[1,2] and hence the demand for a more secure cryptography system has become even more urgent. Quantum cryptography can be a powerful solution to this problem and it is the product of the combination of the fundamentals of quantum mechanics and classical cryptography theory. Unlike the mathematics-based classical cryptography, the security of quantum cryptography is guaranteed by the quantum non-cloning theorem and Heisenberg’s uncertainty principle, which serve as the internal condition and the external protection, respectively. Designing the secure quantum cryptography protocols based on the special properties of the quantum state is an important research direction of quantum cryptography. Quantum cryptography protocols can be subdivided into QKD, quantum secret sharing (QSS), quantum secure direct communication (QSDC), quantum identity authentication (QIA), quantum signature (QS), quantum coin flipping (QCF), quantum money (QM),[3] quantum private query (QPQ),[4–6] and quantum secure computation (QSC),[7,8] among which the latter four have recently become hot topics and QS is an important foundation of the secure quantum information system and quantum cryptography schemes.
So far, quantum signature schemes have been extensively researched for realizing different purposes, for instance, arbitrated quantum signature (AQS),[9–18] quantum homomorphic signature (QHS),[19,20] quantum blind signature (QBS),[21–24] quantum group signature (QGS),[25–28] quantum proxy signature (QPS),[29] quantum digital signature (Q-DS),[30–32] and quantum dual signature (QDS).[33,34] Among these schemes, we focus on the AQS scheme. The frame of the AQS scheme was initially raised by Zeng and Keitel[9] by employing three-particle entangled Greenberger–Horne–Zeilinger (GHZ) states. Curty et al.[11] investigated and argued that the proposal[9] was not clearly operationally defined and ambiguous. Later Zeng gave a more detailed demonstration and presentation[12] of the previous scheme.[9] Next, instead of GHZ triplet states, Li et al.[13] exploited two-particle entangled Bell states to design an AQS scheme, which shows the advantages referring to a better efficiency in transmission and a low complexity in implementation. Zou and Qiu claimed that the above schemes cannot guarantee the disavowal from the receiver and presented an AQS scheme[14] with a public board. Choi et al.[15] also pointed out the security problem on AQS schemes. Li et al.[16] proposed an AQS protocol replacing the quantum one-time pad with the chained CNOT operations. Yang et al. put forward an AQS protocol[17] with cluster states, which can achieve an efficiency with 1. Note that these above-mentioned schemes are based on discrete variable (DV) quantum states.
Up to now, quantum signatures can be categorized into two forms, i.e., a DV-based quantum signature and a CV-based quantum signature. The DV-based quantum signature schemes have achieved a great deal of success, which belong to quantum cryptography schemes. Undeniably, the DV-based quantum cryptography schemes have also lots of limitations and difficulties and they are facing more and more challenges.[35] For one thing, the production and the detection of a single photon are tricky and the generation of entangled photon pairs is also very troublesome. The production efficiency of a single photon is very low and it may suffer from the potential photon number splitting attack.[36] Furthermore, the detection of a single photon is confronted with severe limitations. Correspondingly, in practical experiments, weak laser is applied to replace single photon.[37] For another, the communication rate of DV-based quantum cryptography is relatively low. Under such a circumstance, the CV-based quantum cryptography, which uses strong light replacing the single photon or entangled photon pairs, comes out. Compared to the DV-based quantum cryptography, the CV-based quantum cryptography has the strengths[35] referring to simple preparation, superior transmission rate, high detection efficiency and repetition rate and easy implementation in the experiments. In the CV-based quantum communication protocols, the messages are encoded onto the amplitude and phase of CV-based quantum states and can be transmitted with a greater communication rate, such as CV-based quantum teleportation.[38] The required manipulations and measurements can be realized in quantum optics in a simple and efficient way, and the shift amount in the quadrature phase space can be measured by homodyne detection. Therefore, investigations into the CV-based quantum cryptography are of great significance. In the last couple of years, Zeng et al.[39] initially researched the CV quantum signature algorithm with CV entangled states in 2007, which is a true quantum signature algorithm using a key-pair, i.e., public verification key and private signature key, and exploits a quantum circuit to compare the original states and the decoded states. It provides a fresh idea and a more efficient method to explore quantum signatures. In 2016, we proposed an AQS scheme based on CV coherent states,[18] which serve as the carrier of the signing messages. Its security is guaranteed by the CV-QKD and the CV-based quantum teleportation, which show a potential high-speed AQS algorithm with high communication rate and detection efficiency. In the same year, Huang et al.[40] raised CV-based QIA with a two-mode squeezed vacuum state and coherent state. It is worth mentioning that an AQS scheme is of a better application when compared with a true signature scheme, especially with the reduced requirements on the trustworthiness of the arbitrator.[9]
Motivated by the structure of the AQS with CV-based coherent states, we suggest an AQS scheme with CV-based squeezed vacuum states, which are the simplest squeezed states. The proposed scheme makes the following contributions.
(i) Compared to the above-mentioned DV-based quantum signature schemes, the primary advantage is that the amount of information contained in CV-based quantum states is much larger. Moreover, the CV-based squeezed vacuum states, the carrier of the transmitted messages, are easy to generate and convenient to use. Most importantly, the essential operations, preparation (degenerate parametric process), transmission, manipulation and measurement can be efficiently executed in quantum optics.
(ii) Compared to the existing CV-based quantum signature schemes,[18,39] the proposed AQS scheme is of a better application than a true quantum signature scheme. Additionally, the effect of squeezed states is in principle better than that of coherent states in terms of the encoding efficiency and the communication quality.
(iii) The proposed scheme can be implemented by using sources of an optical parametric oscillator (OPO), beam splitter (BS), amplitude (AM), and phase modulators (PM), which are compatible with standard telecommunication technology.
The rest of this paper is arranged as follows. Section
For a secure quantum signature scheme, there are a few rules[9] to be expected to be accomplished.
i)
ii)
iii)
To simplify the scheme design and the subsequent security analyses, the classical communication is assumed to be performed in the authenticated channel, and the quantum channel from the sender to the recipient is also authenticated. Note that the current error correction and privacy amplification techniques[41] may be employed to realize the authenticated channels and the former can be achieved by communicating 
















As the first stage to the quantum signature scheme, we state how the secret keys and the CV-based quantum entangled states are created and assigned.
As the critical stage to the quantum signature scheme, we elaborate on how to create the signature of the transmitted message. This phase can ensure the integrality and reliability of the message and deter the possible disavowal attacks from Alice.
 | Fig. 2. (color online) The phase space presentation of the squeezed vacuum state 

|
| Table 1.
Encoding and phase angle transformation process. . |
The variances of a vacuum state are given by
 |

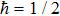
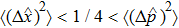
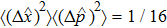
 |
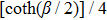

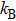
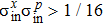
 | Fig. 3. (color online) The relationship 



|
Generally, the Gaussian state can be fully characterized by parameters r, β, angle θ in the coordinates, and the displacement α0. Setting 

 |
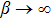
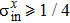
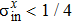
Equation (



As the last stage to the quantum signature scheme, the purpose is to verify the validity of the signature 

To implement quantum teleportation[38] in real experiments, the following inequalities should be satisfied
 |
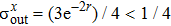
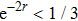
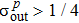
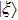
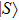
The above-described procedure is the application of the quantum teleportation with the CV-based squeezed vacuum states which is generally evaluated by calculating fidelity F denoting the overlap of the input and output states. F = 0 means that the teleported state is orthogonal to the input state and F = 1 means that 

 |


If an input state is a mixed state (the mixed squeezed vacuum state is regarded as a squeezed thermal state), the fidelity is expressed as
 |


 |
 |
 |
In fact, the comparison of the input squeezed vacuum state 













 |
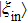

 |
For 




To begin with, we recall that Charlie serves as an important role in the proposed AQS scheme. In the initial stage, Charlie creates the CV-based EPR entangled state and the secret key Ka (Kb) shared with Alice (Bob). In the verification stage, Charlie defines the verification parameter t for comparing the secret quantum states 

From the expression in Eq. (






 |
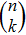
 |
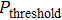
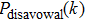
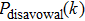

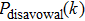
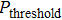
For the purpose of their benefit, a dishonest Bob or an external attacker may try to forge Alice’s signature. In what follows, we show that any attempt to forge the signature 
Assume that Bob is dishonest and (is) in an attempt to forge Alice’s signature 





The dishonest participant generally has more right than an external attacker. We have analyzed that the forgery strategy from the dishonest Bob is impossible to succeed, and hence the attacker is bound to be unsuccessful in our scheme. This is because there is no information about the keys Ka and Kb via the exposure of the public parameters 






From the application’s point of view, the scheme should satisfy that the receiver Bob cannot repudiate his receiving of the signature 



 |


 |

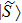
Based on the cryptanalysis in Ref. [53], another disavowal attack strategy by Alice may be successful. For example, when Charlie, sends 





In Subsection 3.2, we have demonstrated that Bob’s forgery strategy by obtaining the key Ka is impossibly successful. However, based on the cryptanalysis in Ref. [53], another forgery attack strategy by Bob without Ka may be successful. For example, we assume that Bob has a valid message-signature pair (








In principle, when playing the role of information carrier, squeezed states are better than coherent states. In our scheme, the original binary-valued messages are encoded onto the CV-based squeezed vacuum states, as listed in Table
We have proposed an AQS scheme with CV-based squeezed vacuum states, which requires three participants to jointly complete the initial phase, the signature phase and the verification phase. In the initial phase, the secure keys are prepared and distributed to the legal participants. In the signature phase, the signature is finally generated by employing the unitary phase transformation and the CV-based quantum encryption algorithm. In the verification phase, the validity of the yielded signature is verified via the comparison of the transmitted messages and the recovered messages with the fidelity and the BS technology. The security of our scheme is ensured by the CV-based quantum teleportation and the CV-QKD. Security analyses demonstrate that the proposed scheme can deter the disavowal and forgery attack strategies with the shared keys. However, it is not resistant to Alice’s disavowal and Bob’s forgery strategies in the circumstance of known message attack, which will be improved in the future study. In addition, the scheme has better coding efficiency and communication performance. Therefore, the proposed AQS scheme may be practical for the general authentication system and the voting mechanism.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] |






















