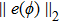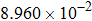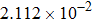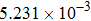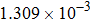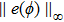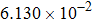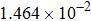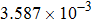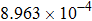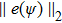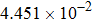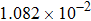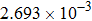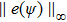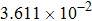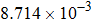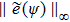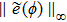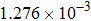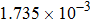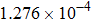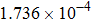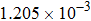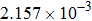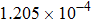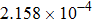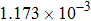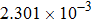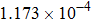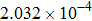In this paper, we consider the following one-dimensional Zakharov system (ZS)^[1] 1 which describes the interaction between high-frequency Langmuir and ion acoustic waves in a plasma. Here, , the unknown complex function ϕ denotes the slowly varying envelope of the highly oscillatory electric field, and the unknown real function ψ represents the fluctuation of the ion density about its equilibrium value. With initial and Dirichlet boundary conditions 2 the Dirichlet initial-value Zakharov equations (1) possess mass and global energy conservation laws (GECL): 3 where .

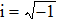
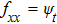
Extensive mathematical and numerical studies have been developed for the Zakharov system during recent decades. Mathematically, the existence and uniqueness, the wellposedness and the regularity of smooth solutions, and the collision of solitons were established by Hadouaj, Bourgain, Colliander, and Fang.^[2–6] Numerically, such as the spectral method,^[7–11] the symplectic and multi-symplectic method,^[12,13] the finite element method,^[14] and the finite difference method^[15–19] have been carried out for the Zakharov system. Nowadays, structure-preserving methods have been more and more popular and successfully applied to various PDEs.^[20–23] To the best of our knowledge, there have been few approaches which can preserve the local energy of the Zakharov system in the literature. This motivates our study to introduce energy-preserving methods for solving the Zakharov system.

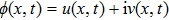
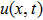
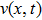
As we all know, the GECL (3) depends on the suitable boundary conditions, such as the periodic or homogeneous boundary conditions. However, in practice, the boundary conditions may not be always suitable in many cases. Actually, the Zakharov system admits a local energy conservation law, which is more essential than the global energy conservation law (3) in physics. Let , where and are real-valued functions. Introducing some intermediate variables, the Zakharov system (1) can be reformed into a combination of ordinary differential equations 4a 4b 4c

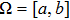
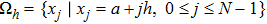
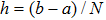
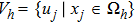
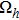
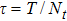
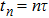
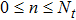
Let N be a positive even integer. The domain is uniformly divided into N subdomains , where . Let be the space of grid functions on . For a positive integer N_t, we denote time step , , . We define According to the discrete Leibnitz rule,^[28] we have

In system (4), discretizing the time and space derivatives by the mid-point rule and leap-frog rule, respectively, we obtain 8a 8b 8c where . Eliminating the auxiliary variables, we obtain a full discrete scheme 9

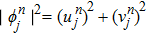
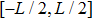
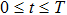
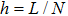
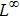
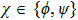
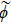
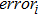
In this section, some numerical experiments are carried out to show the performance of the proposed LEP scheme. Our computations will work on the spatial domain over the time interval with time step length τ and spatial step length . Here N is the number of grid points for the spatial domain. Furthermore, errors between numerical solutions and analytic solutions in L ² and norms are, respectively, defined as where and denotes the numerical solution as the initial value is disturbed, etc. The convergence order is calculated by the following formula where δ_i and denote step size and the corresponding discrete error, respectively.

The invariants-preserving results are shown in Fig. 1. It is easy to find that the local energy is conserved by the proposed LEP scheme throughout the computations. The errors in global mass and global energy, which oscillate near zero in the scale of 10⁻¹²–10⁻¹⁴, indicate the two global invariants are also captured. In order to test the convergence order of the scheme, we solve the problem on the interval [−32,32] with T = 4. The numerical results are given in Table 1, where a second order convergence of the proposed LEP scheme can be explicitly observed. Table 2 indicates the proposed LEP scheme is stable for different initial values.

Fig. 1.

	Figure Option ViewDownloadNew Window
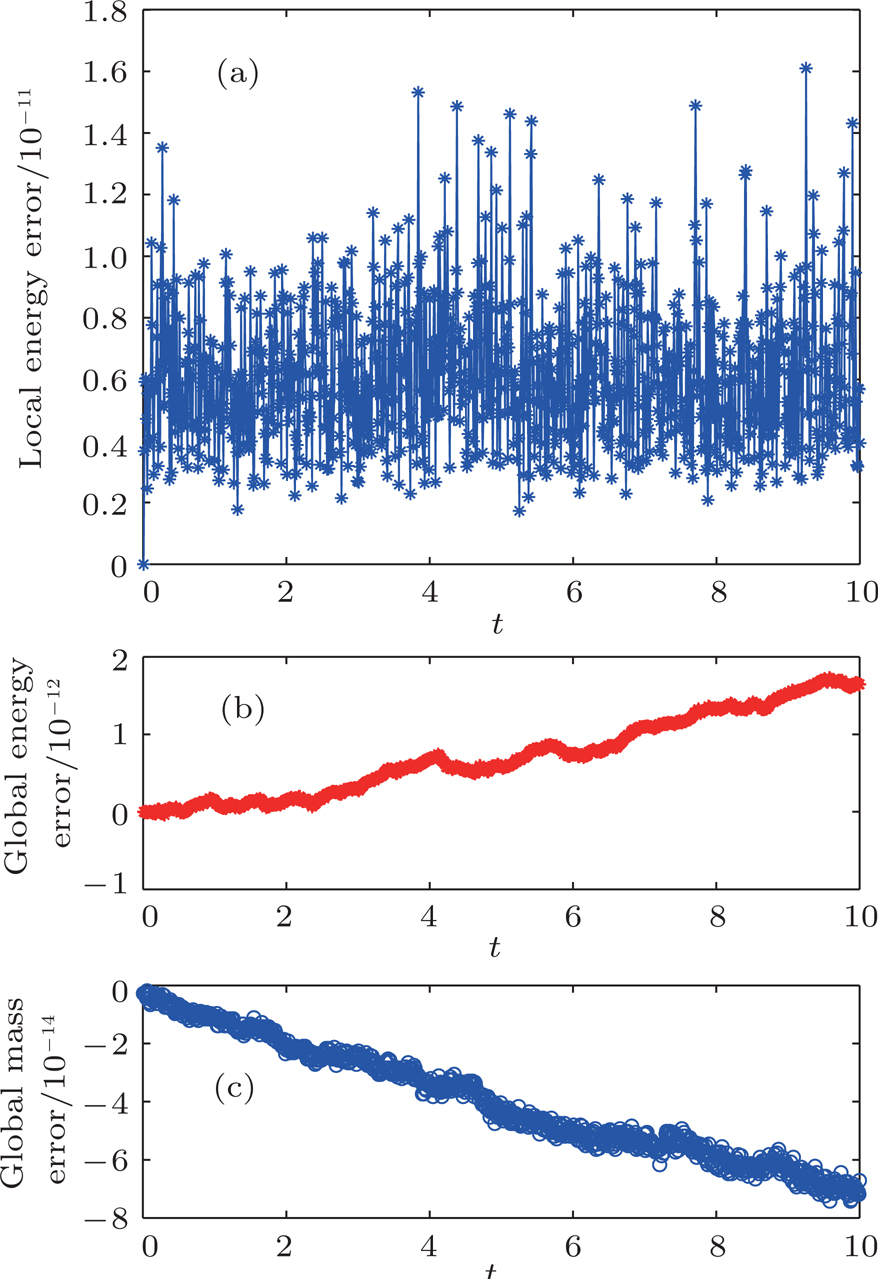	Fig. 1. (color online) (a) The variation of the local energy from t = 0 to t = 10; (b) the variation of the errors in the global energy, and (c) the global mass from t = 0 to t = 10, respectively.

Table 1.

Table 1.

Table 1. Convergence order of the proposed LEP scheme (T = 4, τ = h). . h = τ 0.4 0.2 0.1 0.05 Order – 2.085 2.014 1.998 Order – 2.066 2.029 2.001 0.206 Order – 2.208 2.040 2.007 0.176 Order – 2.287 2.051 2.008

Table 1. Convergence order of the proposed LEP scheme (T = 4, τ = h). .

Table 2.

Table 2.

Table 2. Stability test of the proposed LEP scheme. . λ = 0.001 λ = 0.0001 h τ 0.4 0.4 0.2 0.2 0.1 0.1

Table 2. Stability test of the proposed LEP scheme. .

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) The values of and at different times for Case I [panels (a) and (b)] and Case II [panes (c) and (d)].

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) The errors of global energy and local energy for Case I [panels (a) and (b)] and Case II [panels (c) and (d)].

In the present paper, we proposed a local energy-preserving (LEP) scheme to simulate the Zakharov system. The scheme preserves the discrete LECL in any time–space region, which is independent of the boundary conditions and is more essential than the discrete GECL. If the boundary conditions are suitable, summing the discrete LECLs over all space index leads to the GECLs. The scheme proposed in this paper extends the applying scope of the traditional global energy-preserving algorithm. Numerical results show the excellent performance in conserving local energy, global energy, and mass invariants. What is more, we find that the LEP scheme is stability and a second order convergence can be explicitly observed.

For the local energy conservation law of the Zakharov system (1), we can also use other useful methods to construct local energy-preserving schemes. Actually, we can even propose a series of local momentum-preserving schemes for the Zakharov system, which conserve discrete momentum conservation laws in any time–space region.