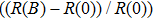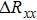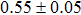|
Ling Jiwei1, 2, Liu Yanwen1, 2, Jin Zhao3, Huang Sha3, Wang Weiyi1, 2, Zhang Cheng1, 2, Yuan Xiang1, 2, Liu Shanshan1, 2, Zhang Enze1, 2, Huang Ce1, 2, Sankar Raman4, Chou Fang-Cheng4, Xia Zhengcai3, ‡, Xiu Faxian1, 2, 5, †
|
|
(color online) SdH oscillations at low fields. (a) The magneto-resistance ratio 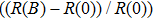 at different angles. The angle of magnetic field is defined as the angle between the magnetic field and the normal of the bc plane (zero degree means that the magnetic field is perpendicular to the bc plane). The maximum MR ratio is approximately 200%. Clear SdH oscillations persist beyond at different angles. The angle of magnetic field is defined as the angle between the magnetic field and the normal of the bc plane (zero degree means that the magnetic field is perpendicular to the bc plane). The maximum MR ratio is approximately 200%. Clear SdH oscillations persist beyond  . (b) The angular dependence of the oscillation frequency, following the cosine law . (b) The angular dependence of the oscillation frequency, following the cosine law  . The red dashed curve indicates the cosine fitting. (c) SdH oscillations at different temperatures. . The red dashed curve indicates the cosine fitting. (c) SdH oscillations at different temperatures. 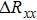 were obtained by subtracting a parabolic background. Inset: Fourier transform of the oscillations at 2.5 K, revealing a single frequency F = 74.6 T. (d) The Lifshitz–Kosevich formula fitting to the oscillation amplitudes at different temperatures. The fit yields the cyclotron effective mass were obtained by subtracting a parabolic background. Inset: Fourier transform of the oscillations at 2.5 K, revealing a single frequency F = 74.6 T. (d) The Lifshitz–Kosevich formula fitting to the oscillation amplitudes at different temperatures. The fit yields the cyclotron effective mass  , where , where  is the bare electron mass. (e) Dingle plot. The oscillation amplitude at 2.5 K decays exponentially. The Dinge temperature fitting yields the Dingle temperature of 15 K. The quantum lifetime obtained is is the bare electron mass. (e) Dingle plot. The oscillation amplitude at 2.5 K decays exponentially. The Dinge temperature fitting yields the Dingle temperature of 15 K. The quantum lifetime obtained is  s. (f) Landau index plot. Inset: integers correspond to the valleys in the conductance spectrum. All the data align well on a straight line. The red dashed line is the linear fit using s. (f) Landau index plot. Inset: integers correspond to the valleys in the conductance spectrum. All the data align well on a straight line. The red dashed line is the linear fit using  . The intercept . The intercept 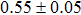 corresponds to a trivial Berry phase either for 2D or 3D system. corresponds to a trivial Berry phase either for 2D or 3D system.
|