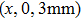† Corresponding author. E-mail:
We propose a scheme to produce a uniform magnetic field with a system comprising a pair of coils and an atom chip. After optimizing the parameters of the chip wires, we improve the homogeneity of the magnetic field by two orders of magnitude. We exhibit that this method can be applied in the investigation of Efimov physics in 87Rb–40K mixture.
As a powerful tool to control interactions between atoms, magnetic Feshbach resonances have been widely applied to explore a vast array of phenomena in ultracold atomic and molecular quantum gases.[1,2] This has led to a number of intriguing physical phenomena such as the observation of a “Bosenova” from a controlled collapse in a Bose–Einstein condensate (BEC),[3] the sonic analog of a gravitational black hole in a BEC,[4,5] the creation of ultracold molecules,[6] and the investigation of Efimov physics in three-body systems.[7–9] In many experiments, a large scattering length 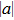
Several kinds of coils have been applied to generate uniform magnetic fields, of which the most commonly used is a Helmholtz coil.[10] A Helmholtz coil consists of two identical coaxial circular coils separated by a distance h which equals to the radius R of the coil, and each one carries an equal electric current in the same direction. Another important coil, the saddle-shaped coil,[11] can produce a magnetic field with higher uniformity than a Helmholtz coil of the same scale. However, both cannot be used in some experiments owing to their geometry or dissipation power. For example, there are tens of windows in the vacuum chamber of the multipurpose cold atomic experimental device, in which we utilize the design. The coils should not block any light path around the chamber. For some experiments involving Feshbach resonance between 87Rb–40K mixture, a uniform magnetic field as high as 550 G with power dissipation less than 1000 W is required. In the evaporative cooling phase, the coils are also utilized to generate a quadrupole magnetic field for trapping atoms.[12] Therefore, neither a Helmholtz coil nor a saddle-shaped coil satisfies all these demands. In our preliminary design, we set a pair of coils at the exterior regions of the top and bottom windows of the chamber, which can produce 550 G with power dissipation of approximately 800 W, but it does not meet the requirement for the uniformity of the magnetic field.
In this paper, we propose an alternative way to improve the homogeneity, which combines magnetic fields created by currents in both macroscopic coils and wires on a chip. Our calculation shows that the magnetic field produced by the chip wires cancels most of the inhomogeneity of the magnetic field created by the macroscopic coils. As an example of an application, we demonstrate that this system can be used to explore the Efimov effect in 87Rb–40K mixture with a scattering length up to 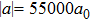
The magnetic field generated by the current in a single coil is[13]
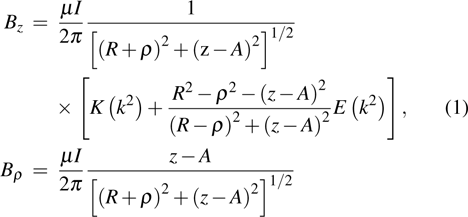
The configuration of the coil assembly is shown in Fig. 
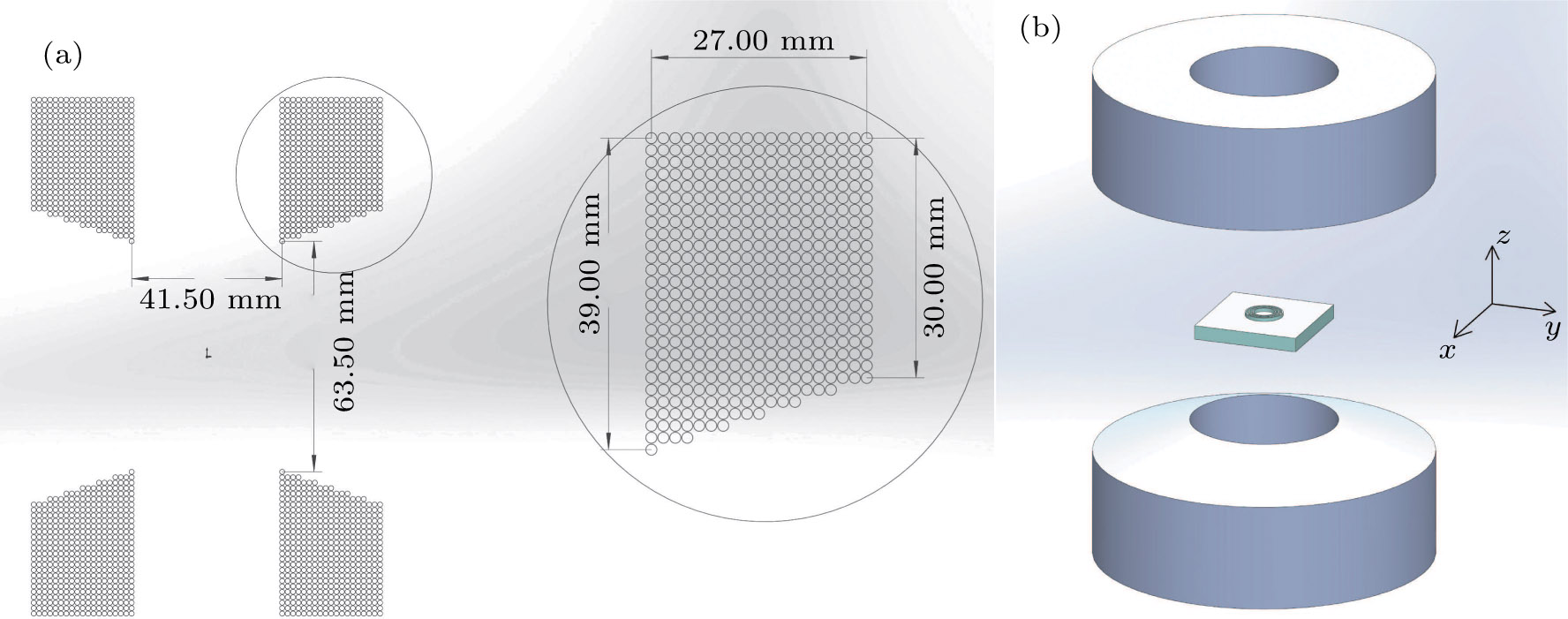 | Fig. 1. (color online) (a) Structure and winding details of coils. (b) A sketch of the coils atom chip combined system. |
The foregoing calculation indicates that the magnetic field along the z axis can be expressed as
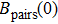
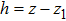
The magnetic field around the height h0 in the symmetry axis, which is produced by the current in a single circular coil on the chip, can be expanded as
1) A3 equates to zero. This can be achieved by adjusting the radius of the ring after 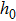

For several rings, we set their radius around 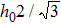
2) To eliminate the terms of h2, the coefficients should satisfy 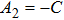
3) To eliminate the terms of h, we adjust the position of the chip surface z1. It is easy to find that the condition is
4) To generate the required magnetic field, we change the current in the pairs and chip wires with the same factor.
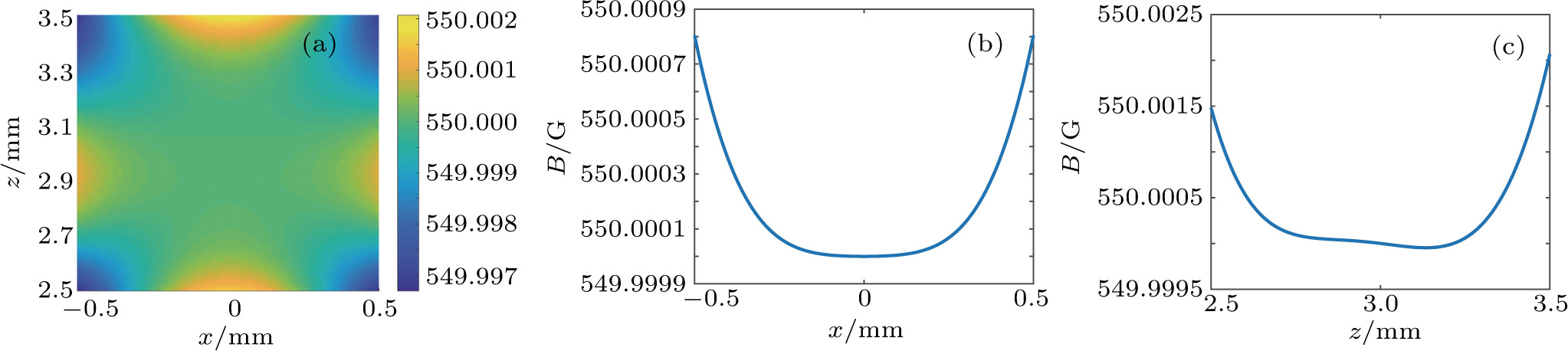
Owing to the zero-divergence of the magnetic fields and the axial symmetry of the system, once we reduce the space variation of the magnetic field along the z axis, the space variation of the magnetic field along the x and y axes is also canceled within a limited region.
We then perform a numerical simulation with the above steps. First, we set 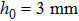

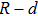
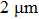
We now estimate the parameters following steps 1 to 3 when the current in the coils is 20.082 A. We obtain R=3.4641 mm and 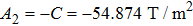

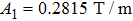
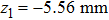
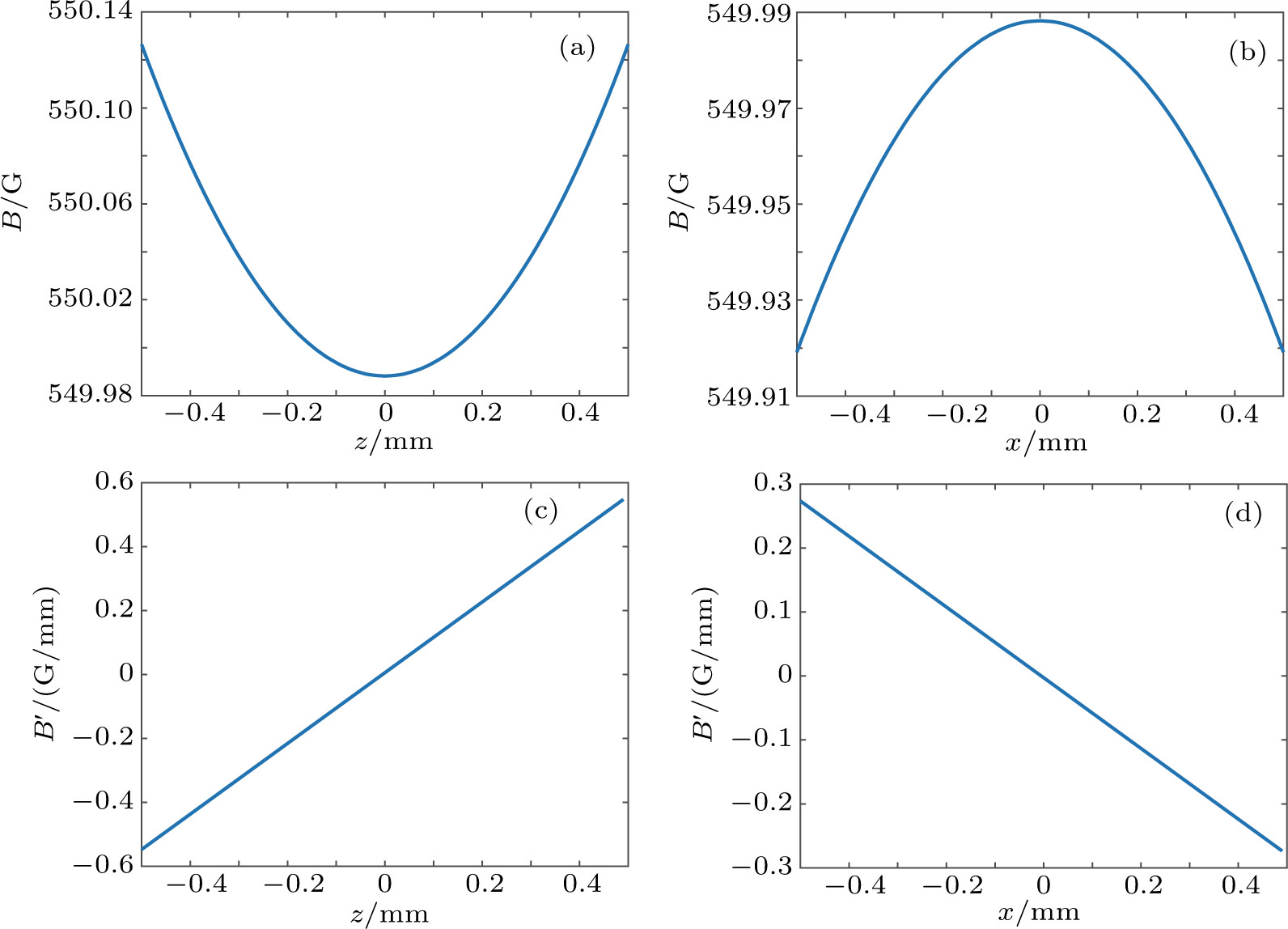
The first step of the parameter estimation process is based on a single ring with a thin wire that is slightly different from the real case. By slightly modifying z1 to −5.5809 mm, we can further improve the homogeneity of the magnetic field. With the above parameters, the magnetic field strength at the central area is approximately 538.203 G. To compare with the case of the coil assembly, we adjust the value to 550 G by multiplying a factor of approximately 1.022 to all currents.
Figure 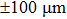

To avoid the extra magnetic field generated by currents in wires that connect the rings on the chip and the current feed through, each pair of wires carrying the input and output currents is set closely parallel on the other side of the chip. They connect the corresponding rings by using through-wafer interconnect technology.[16] The distance between each pair of parallel wires is only tens of microns, so the magnetic fields in our area of concern cancel each other. The chip can be glued on a copper support, which is fixed to the vacuum chamber. To avoid the possible conduction between the chip wires on the rear side with the metal mount, an insulating layer of silicon dioxide is coated on the rear side of the chip. The typical resistance of all the chip wires is approximately 10 Ω, so the system adds only approximately 30 W of power. The power is still in the permissible range.
Because the atomic cloud is 3 mm from the chip surface, there is enough space to put another layer of chip covering on it. The added top layer can be fabricated by other wires for different experimental purposes. It is also beneficial that the top layer is a mirror with high optical quality, which is a benefit to some experiments involving a reflection image or optical lattices.[17,18]
We now turn our attention to Efimov physics, which is a universal phenomenon in quantum three-body systems. Efimov predicted a universal set of bound trimer states appearing for three identical bosons with a resonant two-body interaction.[7] These states even exist in the absence of a corresponding two-body bound state. Efimov-related loss resonances as a function of a have been observed in ultracold homonuclear and heteronuclear atomic systems.[8,9] However, these resonances in the rates of inelastic collisions between three atoms of 87Rb–40K mixture have not been observed.[19,20] Further work is needed to resolve this contradiction. In 87Rb–40K mixture, the dominant three-body recombination process is 87Rb+87Rb +40K, and the 87Rb+40K+40K loss is suppressed by Fermi statistics. 87Rb and 40K atoms are prepared in the 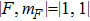
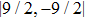
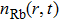
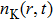

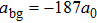
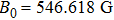
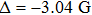
At negative a,
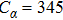
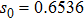
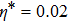
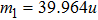
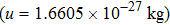
In real experiments, owing to the inhomogeneity of the magnetic fields, the loss rate coefficient α has spatial variation. Thus, the atom loss rate should be rewritten as
The Efimov effect is a few-body physical effect, so the temperature of 87Rb atoms should be higher than the Bose–Einstein condensation transition temperature 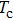
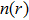
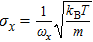
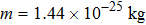
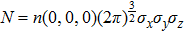
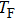
Our calculation is based on two sets of parameters. The parameters of the first group are 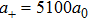
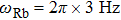
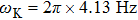
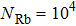
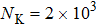
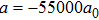
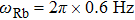
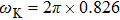

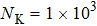
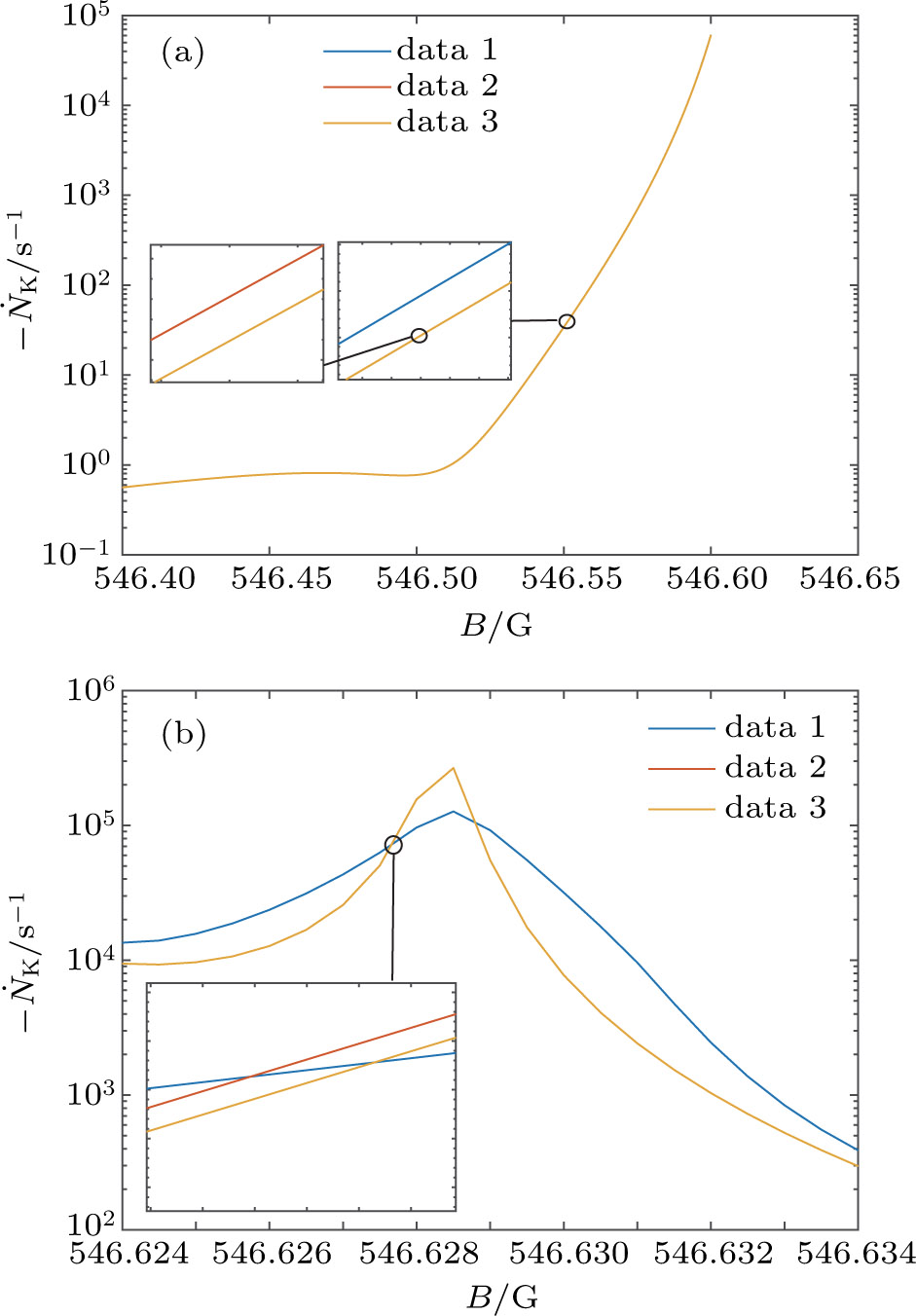
Another undesirable effect of inhomogeneous stray magnetic fields is that they limit the lowest atom temperature. This effect is more critical than the broadened resonance peaks. The atoms are trapped in an optical trap so the optical potential is at the same order of temperature as the atomic cloud. If the potential induced by inhomogeneous stray magnetic fields is comparable with the optical potential, the atomic cloud will escape from the trap. In the experiment we discussed above, the observation range of 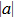
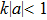
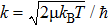
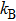

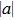
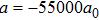
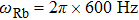
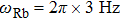
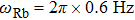
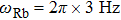
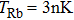
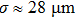
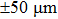
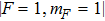
We then check another group of experimental parameters. When the trap frequency 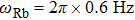
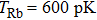
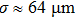
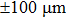
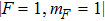
Our method also has the benefits of fast and precise control of the magnetic fields. It is difficult to implement precise and fast control of the current in regular coils owing to their considerable inductance. The inductance of the chip wires is lower by several orders, so the response time can be reduced remarkably. This is crucial for the kind of experiment where the magnetic field is set to the value near the resonance position. For instance, in the preceding section, we discussed the experiment with the scattering length 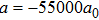
In conclusion, we have proposed a scheme to obtain a uniform magnetic field by combining the magnetic fields generated by currents in macroscopic coils and chip wires. The homogeneity of the magnetic field has been improved by two orders of magnitude compared with the method that uses only the coil assembly. This method can be applied in the experiment for investigating the Efimov effect in 87Rb–40K mixture. The test range of the scattering length is extended to more than 55000a0, which is sufficient to compare with the theoretical prediction. Recent experimental and theoretical work already revealed the Efimov resonance departure from the universal prediction.[22] Our scheme provides an experimental approach for further investigation.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |