† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11274378), the Key Research Program of the Chinese Academy of Sciences (Grant No. XDPB08-3), and the MOST of China (Grant No. 2013CB933401).
It is commonly known that the hydrodynamic equations can be derived from the Boltzmann equation. In this paper, we derive similar spin-dependent balance equations based on the spinor Boltzmann equation. Besides the usual charge current, heat current, and pressure tensor, we also explore the characteristic spin accumulation and spin current as well as the spin-dependent pressure tensor and heat current in spintronics. The numerical results of these physical quantities are demonstrated using an example of spin-polarized transport through a mesoscopic ferromagnet.
The hydrodynamic equations satisfied by mass density, pressure, flow velocity, heat, and entropy can be derived from the classical Boltzmann equation.[1] The quantum fluid equations derived by Madelung[2] from the Schrodinger equation have been applied to semiconductor device modeling.[3] The usual hydrodynamic equations describe the time and spatial variations of a fluid without spin. However, in some special fluids named Fermi liquids,[4–6] e.g., He3, the spin plays an important role. Fermi liquids are governed by the Landau-Boltzmann equation,[7] and the conservation laws and spin dynamics from this equation indicate that the spin degrees of freedom have an important influence. In fact, one can describe the motion of a quasi-particle in a Fermi liquid by the spin hydrodynamic equations.[8,9] In the later, Landau’s theory was extended to a degenerate electron liquid,[10,11] in particular ferromagnetic metal.[12–17]
Ferromagnetic metals, such as Fe, Co, and Ni, are the key ingredients in spintronics devices. The tunneling magnetoresistance[18,19] (TMR) and spin transfer effect[20–23] in spintronics are all dependent on the electronic spin-polarized transport in the ferromagnets,[24,25] and the electrons in a ferromagnet can be treated as a Fermi liquid. The spin current in a ferromagnetic metal satisfies the corresponding equations of continuity,[26–29] except for the charge current, which can be regarded as one of the spin-dependent hydrodynamic equations for charge density. The spin-dependent heat current has been studied in multilayers[30,31] and a new branch of spintronics, named spin caloritronics,[32,33] has emerged. However, the balance equation for the spin-dependent heat current has not been investigated. Moreover, it is worthwhile to further explore the spin-dependent balance equations corresponding to the momentum and entropy of spintronics.
The spinor Boltzmann equation is a powerful tool to study the spin-polarized transport of electrons in spintronics,[34,35] and includes spin freedom in the quantum Boltzmann equation. In 1957, the spinor Boltzmann equation was utilized to investigate a Fermi liquid by Silin.[10,11] As the usual hydrodynamic equations can be obtained from the classical Boltzmann equation, we expect that similar spin-dependent balance equations may also be obtained from the spinor Boltzmann equation,[34] and will be different from the usual hydrodynamic equations. In this paper, we derive the spin-dependent balance equations for the charge density, pressure, flow velocity, heat, and entropy. While some of the corresponding balance equations are not closed, as in the classical hydrodynamic equations, we obtained statistical expressions for the above spin-dependent physical quantities that are relevant to spintronics. In the final chapter, we provide a simple example to demonstrate the physical quantities in the spin-dependent balance equations.
The spinor Boltzmann equation is an equation of motion for the spinor density matrix. The spinor density matrix satisfies the quantum Liouville equation, and after the quantum Wigner transformation, the spinor density matrix can be related to a spinor distribution function 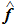



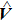


In this section, we will derive the balance equations from the spinor Boltzmann equation (

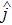
The expansion of the spinor and spinor current densities by the unit and Pauli matrices are
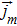
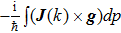
In the formalism of the spinor Boltzmann equation, the spinor momentum density can be defined as

If we further expand the spinor pressure tensor by the Pauli matrices,
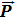
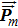

If we define the spinor internal energy density as
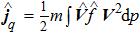


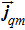
The last balance equation is the entropy balance equation, and we now derive the spin-dependent form. If we define the spinor entropy density as


As an example, we consider the spin-dependent transport through a one-dimensional mesoscopic ferromagnet. At a certain bias, the system will arrive at a steady state after the relaxation time. In this paper, we only investigate the physical quantities in the steady state, where 

The numerical results for the charge density and charge current as a function of position are shown in Figs.
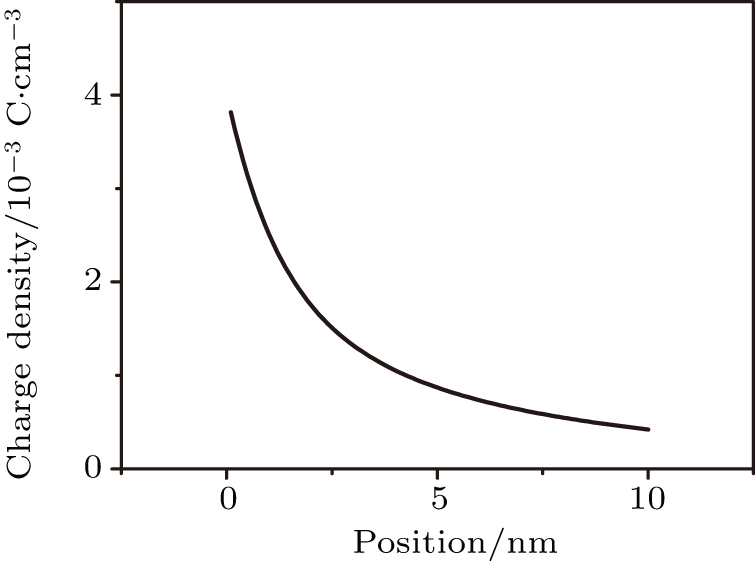 | Fig. 1. (color online) Charge density as a function of position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
 | Fig. 2. (color online) Charge current versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
 | Fig. 3. (color online) Three components of spin accumulation versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
 | Fig. 4. (color online) Three components of spin current versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
 | Fig. 5. (color online) The xx-component of the pressure tensor versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
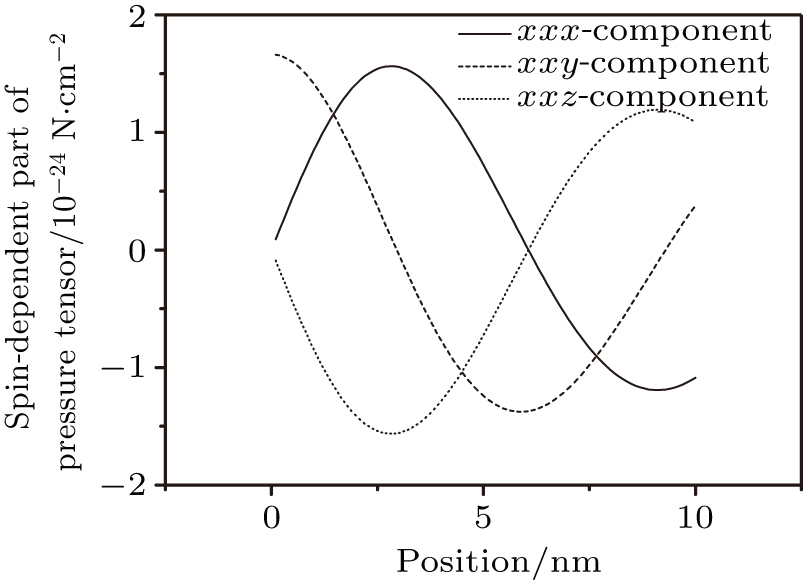 | Fig. 6. (color online) Spin-dependent part of pressure tensor versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
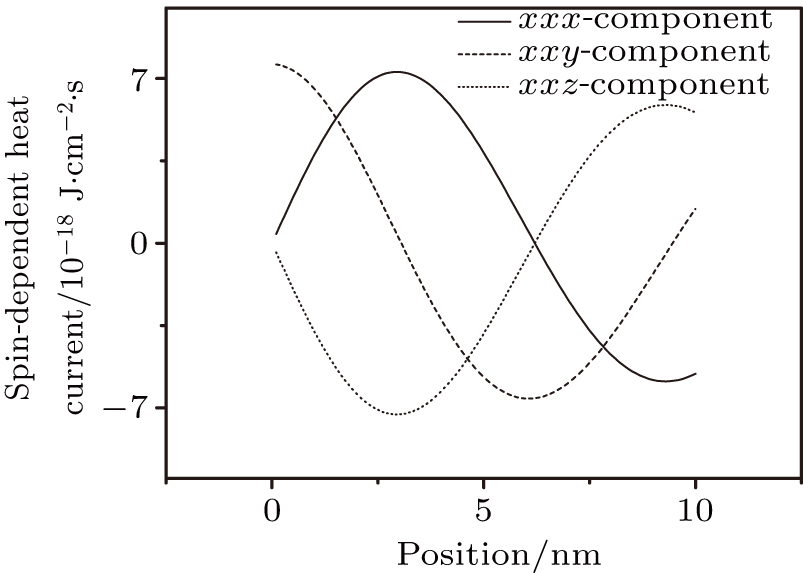
 | Fig. 7. (color online) Heat current versus position. The momentum relaxation time is τ = 0.01 ps, and the electric field E = 1 mV/nm. |
In this paper, we derived the spin-dependent balance equations from the spinor Boltzmann equation. The charge density and charge current, spin accumulation and spin current, and spin-dependent pressure tensor, as well as the thermal and entropy currents were investigated in spintronics. The numerical results for these physical quantities are shown in Figs.
It should be highlighted that the balance equations in our manuscript are not closed as the usual hydrodynamic equations, and the equations depend on the scalar and vector distributions. However, it is useful to study the physical quantities in the hydrodynamic equations by the statistical method that is spin-dependent. In the derivation of the quantum Boltzmann equation using nonequilibrium Green function theory, Mahan[26] proved that if the lesser (greater) self-energy can be expressed as the product of the lesser (greater) Green function and another single-particle Green function, then the continuity equation for the charge density and current is closed. Moreover, the contribution from the scattering terms tends to zero. However, we cannot assure the validity of this assumption in the spin-dependent case, so generally speaking, we should keep the scattering terms in our balance equations which are therefore not closed. The scattering terms in the spin-dependent case[27,28] are complicated to calculate and the relaxation time approximation is usually adopted to simplify them. The development of other approximations for these scattering terms are important.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |