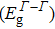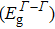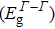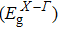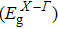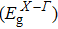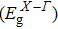† Corresponding author. E-mail:
Structural, electronic, and optical properties of alloys BexMg1−xX (X = S, Se, Te) in the assortment 0 < x < 1 were theoretically reported for the first time in zinc-blende (ZB) phase. The calculations were carried out by using full-potential linearized augmented plane wave plus local orbitals (FP-LAPW+lo) formalism contained by the framework of density functional theory (DFT). Wu–Cohen (WC) generalized gradient approximation (GGA), based on optimization energy, has been applied to calculate these theoretical results. In addition, we used Becke and Johnson (mBJ-GGA) potential, modified form of GGA functional, to calculate electronic structural properties up to a high precision degree. The alloys were composed with the concentrations x = 0.25, 0.5, and 0.75 in pursuance of ‘special quasi-random structures’ (SQS) approach of Zunger for the restoration of disorder around the observed site of alloys in the first few shells. The structural parameters have been predicted by minimizing the total energy in correspondence of unit cell volume. Our alloys established direct band gap at different concentrations that make their importance in optically active materials. Furthermore, density of states was discussed in terms of the contribution of Be and Mg s and chalcogen (S, Se, and Te) s and p states and observed charge density helped us to investigate the bonding nature. By taking into consideration of immense importance in optoelectronics of these materials, the complex dielectric function was calculated for incident photon energy in the range 0–15 eV.
The continuously growing research in the field of optoelectronics is due to the common and potential use of optoelectronic devices, whose technological applications are strongly based on nature of bad gap of an optical material. The direct band gap materials are needed for electroluminescent devices instead of indirect band gap materials as phonons involvement in emission or absorption process makes them optically inactive. Considerable attention has been devoted towards studies of alkaline earth chalcogenides because of their technological importance with a wide range of applications ranging from catalysis to microelectronic.[1,2] Among the alkaline earth chalcogenides, Mg chalcogenides with large band gaps and low dielectric constants have attracted a great deal of attention due to their possible use in blue and ultraviolet (UV) wavelength optics as well as in high-temperature electronics.[3–6] Moreover, a large potential for protective coatings is anticipated for these semiconductors because of their hardness, enormous thermal conductivity, high melting point, and huge bulk modulus. The existence of these semiconductors in four crystalline phases, rocksalt, zinc blende, wurtzite, and nickel arsenide, has triggered significant experimental and theoretical efforts in order to assess the relative importance of these four phases.[7]
Beryllium chalcogenides are of special importance among II–VI compounds because of the lowest mass of Be among group-II elements and having one filled electronic shell. Be-chalcogenides compounds show enhanced rigidity and stability due to their huge bulk moduli.[8] Moreover, the lattice constants of BeS and BeTe are nearly equal to those of GaAs and ZnSe.[9] These characteristics extensively affect physical properties like lattice dynamics,[10] electronic band structures,[11] and bond polarity.[12] On account of the above facts, II–VI mono-chalcogenides can be considered as the most promising candidates for optoelectronic devices.[13,14] In order to have these physical properties continuously varying according to technological requirement, ternary Be-chalcogenides, e.g., BexZn1−xSe[11] or BexMg1−xSe, are modeled. However, the lattice constant of the said ternaries undergoes significant change due to variation in composition. On the other hand, in quaternary Be-chalcogenides composed of BeyMgzZn1−y−zSe, the lattice constant remains unchanged if an appropriate ratio of Be, Mg, and Zn is followed while a band gap variation from 2.7 eV to 4.5 eV is also possible.[15] In addition to fundamental band gap change, higher band gaps (i.e., E1 and E2) are also significantly affected owing to gradual replacement of Zn by Be and Mg. Be-chalcogenides, owing to their large bandgaps, are expected to play a key role in the field of green semiconductor laser. Recently, Be-doped II–VI compounds such that BeZnTe and ZnBeSe have been studied extensively because of their technological importance.[16,17]
Recently, intensive attention has been drawn towards the beryllium chalcogenide alloys due to strong covalent bonding and lattice hardness present in them. The technique molecular beam epitaxy (MBE), with high degree of crystalline quality, is exercised in growing the beryllium containing alloys. Furthermore, these alloys significantly extend the lifetime of the devices on incorporation in LEDs.[18] We believe that advanced research can solve the problem of degradation of II–VI family devices and the mBJ-exchange potential helps to overcome this problem. In this connection, the mBJ-GGA potential within FP-LAPW+lo method is employed for the binaries MgS, MgSe, MgTe, BeS, BeSe, and BeTe and their corresponding ternaries to probe their optical band gaps along with other physical properties. Up to now, in spite of their particularly essential character in device manufacture, no wide-ranging theoretical work has been reported on ternaries. In the existing study, ab-initio calculations have been executed to investigate some physical properties of these alloys in opto-electronic devices as concerning their potential application.
The bulky supercell and arbitrary allocation point defects are constructed on the host lattice to give non-stoichiometric compounds with determined point defects. In order to mimic the statistics of random alloys adequately, a large supercell is required. In this study, the special quasi-random structure (SQS) scheme recommended by Zunger et al.[19,20] is applied due to computational prohibition of density functional theory (DFT)[21] based ab-initio calculations. For the small unit cell (having 8–32 atoms per unit cell) periodic structures, the specially designed SQSs are used, which resemble best pertinent local pair and multisite association functions of the random substitutional alloys. Including full-potential methods, any DFT method is capable of applying for SQSs due to their small size.
The random alloys association does not persist precisely in periodic structure after an interval of definite distance. This problem can be solved by the edifice of bulky supercell, though; the increase in number of atoms in a supercell becomes more expensive with first-principles calculations. Established on the circumstance that physical properties may be determined by microscopic length and local randomness, which are not pretentious by the bulk of supercell, Zunger et al.[19,20] suggested creation of SQS supercells with the improvement of separation of their size on customer choice. In the existing work, a restrictive incident of tiny supercells well-matched with the components in percentage is consequently used.
Therefore, the Be1−xMgxX alloys are machinated in expressions of periodically recurrent supercells in systematic structure with desired compositions. We deliberate an eight-atom cubic lattice by means of concentrations at x = 0.25, 0.5, and 0.75 of Be1−xMgxX alloy in ZB phase to pursue their physical properties. For making an SQS, it is obligatory to replicate the structural correlation function of arbitrary alloy prudently for the first small number of neighboring shells, consequently these correlation functions are vital for the characterization of SQS. The structures are utilized in current study to represent random alloys at x = 0.25/0.75 and x = 0.50 belonging to the eight atom SQS. The elementary benefit of the SQS approach is that it assists overwhelmed restrictions, while studying several disordered solid solutions of physical properties by permitting for exchange of atoms at lattice locations as the subsequent structures replicate the average correlation functions of the arbitrary substitutional alloys.
Self-consistent calculations for BexMg1−xY (Y = S, Se, Te) alloys in zinc blende phase are performed using a relativistic FP-LAPW+lo method to elucidate the Kohn–Sham equations as applied in the WIEN2K code.[22] The interchange correlation prospective for these alloys is computed with the Wu and Cohen generalized gradient approximation (GGA-WC).[23] However, the mBJ-GGA[24] functional is utilized to proceed electronic band structure calculations. This functional is modified from GGA and uses both mBJ XC potential and GGA correlation potential to perform energy band gap calculations as accurately as the GW calculations which are computationally expensive. This FP-APW+lo method employs the division of space into muffin-tin spheres. These non-overlapping spheres are separated by interstitial regions. It also involves the expansion of basic functions into Fourier and spherical harmonic functions inside the interstitial region and spheres, respectively.
This research manifests the fully relativistic treatment of core electron states of Mg, Be and chalcogen (S, Se, Te) atoms are preserved semi-relativistically with valance electrons. For individual sorts of these alloys, to cease the core escape and obtain the total energy coming together by changing the k-point and plane wave limit, appropriate muffin tin radius RMT is designated and the determined angular momentum (lmax) for the wave function is conceded out equal to lmax = 10 whereas the charge density is Fourier prolonged up to Gmax = 16 (Ryd)1/2. The plane wave cutoff of Kmax = 7.0/RMT has been designated for the extension of the wave function in the interstitial region for all the compounds and Kmax = 8.0/RMT for their alloys. The RMT values for Be, Mg, and chalcogen (S, Se and Te) have been taken to be 2.26 a.u, 2.50 a.u, and 1.97 a.u, 2.08 a.u, 2.26 a.u, respectively. A mesh of 2000 special k-points for binary compounds and their ternary alloys are taken to check self-consistent convergence in the irreducible wedge of Brillouin zone. The total energy variance stuck between following iterations is occupied to be fewer than 0.00001 Ryd per formula unit.
First of all, the theoretical modeling of the binary compounds Mg-chalcogen (S, Se, and Te), Be-chalcogen (S, Se, and Te) as well as their alloys for the configurations x = 0.25, 0.5, and 0.75 is carried out towards structural properties investigation. The SQS approach is applied by obtaining the small-unit-cell periodic structures for compositions x = 0.25, 0.50, and 0.75 in an eight atom cubic lattice. The ordered zinc-blende structures at x = 0.25 and 0.75 are obtained with space group #215_P-43m respectively, whereas for x = 0.50 the ordered structure is also eight atom with different space group #16_P222. Symmetry lattice constant ao and bulk modulus B0 have been computed by appropriate Murnaghan equation of states[25] to the entire energy versus different volume curve. The results displayed in Table
| Table 1.
Predicted equilibrium lattice constant and bulk modulus for BexMg1−xX (X = S, Se, Te) alloys and their binary compounds compared to available experimental and other theoretical results. . |
The investigation of electronic band structure (EBS) of a material is extensively important to understand its electronic properties along with valuable information regarding its potential practical use in fabricating new electronic devices. In this study, the theoretically calculated lattice constants are used to calculate the EBS dispersion in k-space beside the extraordinary symmetry directions in the irreducible Brillouin zone of the binary compounds Mg-chalcogen (S, Se, and Te), Be-chalcogen (S, Se, and Te) and their alloys for x = 0.25, 0.5, and 0.75 by employing the GGA and mBJ-GGA functionals. The computed band gap (energy variance between the top and the bottom of valence and conduction bands respectively) values are given in Table
| Table 2.
Direct and indirect band gap values of BexMg1−xX (X = S, Se, Te) alloys obtained by using WC GGA and mBJ-GGA approximations. . |
It is noted that Mg-chalcogens (S, Se, and Te) are direct band gap semiconductors, while Be-chalcogens (S, Se, and Te) are indirect band gap semiconductors. The band gaps of these binary semiconductors are in good agreement with experimental results (see Table
 | Fig. 2. Schematic representation of calculated band structures for BexMg1−xX (X = S, Se, Te) alloys using GGA functional with concentration x = 0.25, 0.50, and 0.75. |
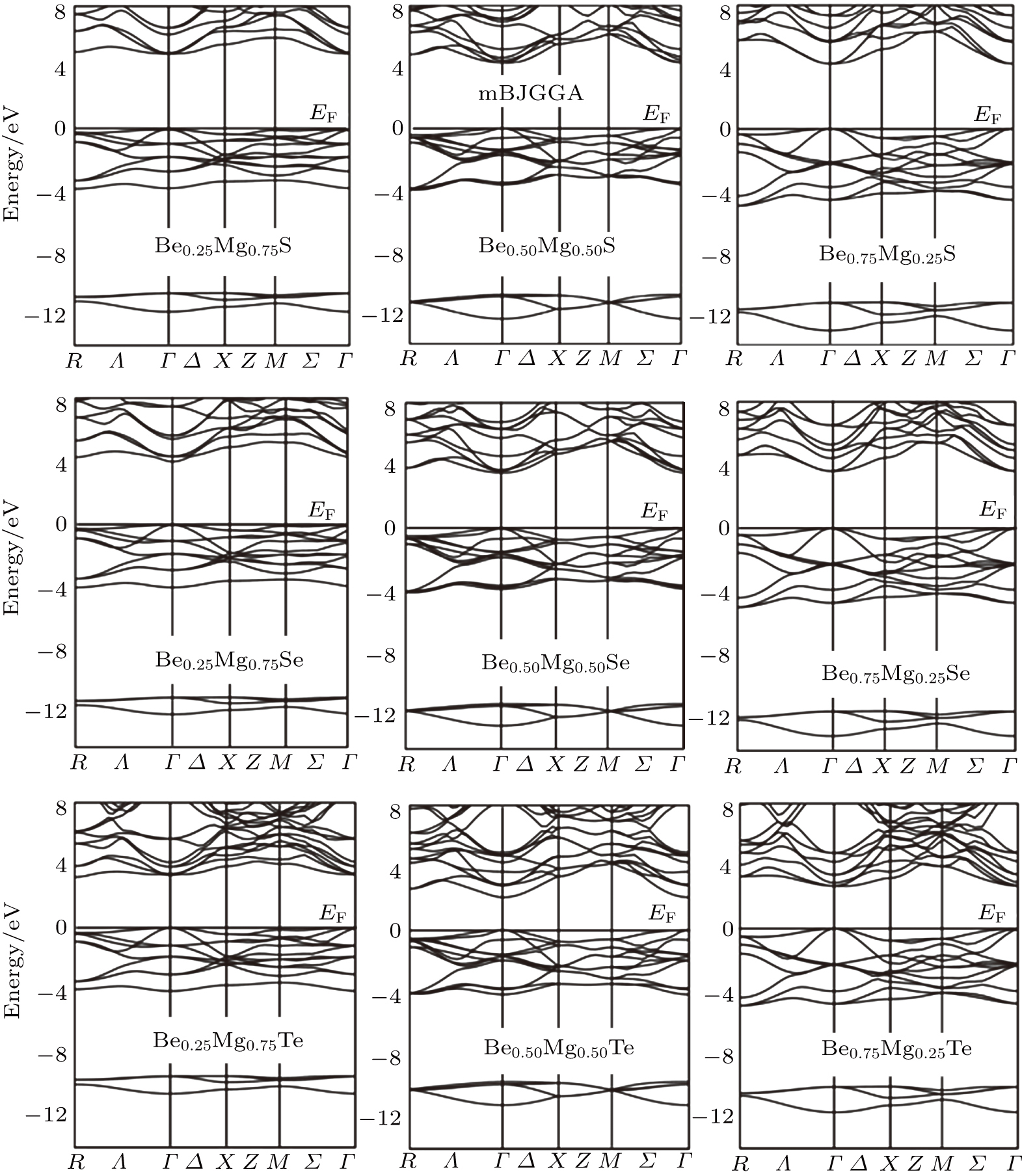 | Fig. 3. Schematic representation of calculated band structures for BexMg1−xX (X = S, Se, Te) alloys using mBJGGA functional with concentration x = 0.25, 0.50, and 0.75. |
In Fig.
 |
 |
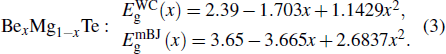 |
Equations (
 | Fig. 5. (color online) Total density of states (TDOS) along with partial density of states (PDOS) using GGA and mBJGGA functionals at x = 0.25 for BexMg1−xX (X = S, Se, Te) alloys. |
It is to orate stating at this point the consequence of supercell bulk of the compounds under study on the electronic properties. As stated previously, we have also executed band structure computation by means of larger (32-atom) supercells to understand the effects instigating from cumulating the numeral of neighboring atoms and symmetry decline on the electronic properties. Owing to decline of crystallographic equilibrium, at extraordinary symmetry points (excluding Γ-point) the band structure sketches for 8 and 32 atoms cells display significant dissimilarities, though, the direct (Γ–Γ) band gaps computed using WC-GGA, EV-GGA, and mBJLDA stay unaffected.
The electronic densities of states (TDOS and PDOS) for BexMg1−xY (Y = S, Se, Te) alloys at x = 0.25 with GGA and mBJ-GGA functionals are displayed in Fig.
Inspecting the charge density maps, one is fully prompt to analyze the chemical bonding nature in a compound. Here, we use WC-GGA results to calculate outline maps of electronic charge density in (1 1 0) plane of BexMg1−xX (X = S, Se, Te) ternaries at x = 0.25 as depicted in Fig.
The optical properties of a material provide a sound understanding of its nature as well as a series of its optoelectronic applications.[35–37] In this connection, the optical parameters of the alloys BexMg1−xX (X = S, Se, Te) at x = 0.25, 0.50, 0.75 and their respective binaries are listed in Table
| Table 3.
Calculated optical parameters for BexMg1−xX (X = S, Se, Te) alloys at different Be concentrations. . |
The energy eigen values along with electron wave functions take part in calculating the part εimaginary(ω) of DF, and εimaginary(ω) has strong correlation with joint DOS as well as with the momentum matrix element. These can be considered as natural output as band structure calculations. Among the DF associated direct and indirect interband transitions, the later transitions involve phonons scattering and are negligible due to their small contribution to DF.[30] However, the process includes all the promising transitions while going from occupied to unoccupied states is executed to acquire the direct interband contributions to εimaginary(ω) part of DF. This imaginary part facilitates working out the εreal(ω) part of DF with the support of Kramers–Kronig relations.[38]
In order to have significantly improved band structure calculations, the two parameters, energy site and comparative amplitudes of explicit absorption, in DF are of great importance. Referring to Figs.
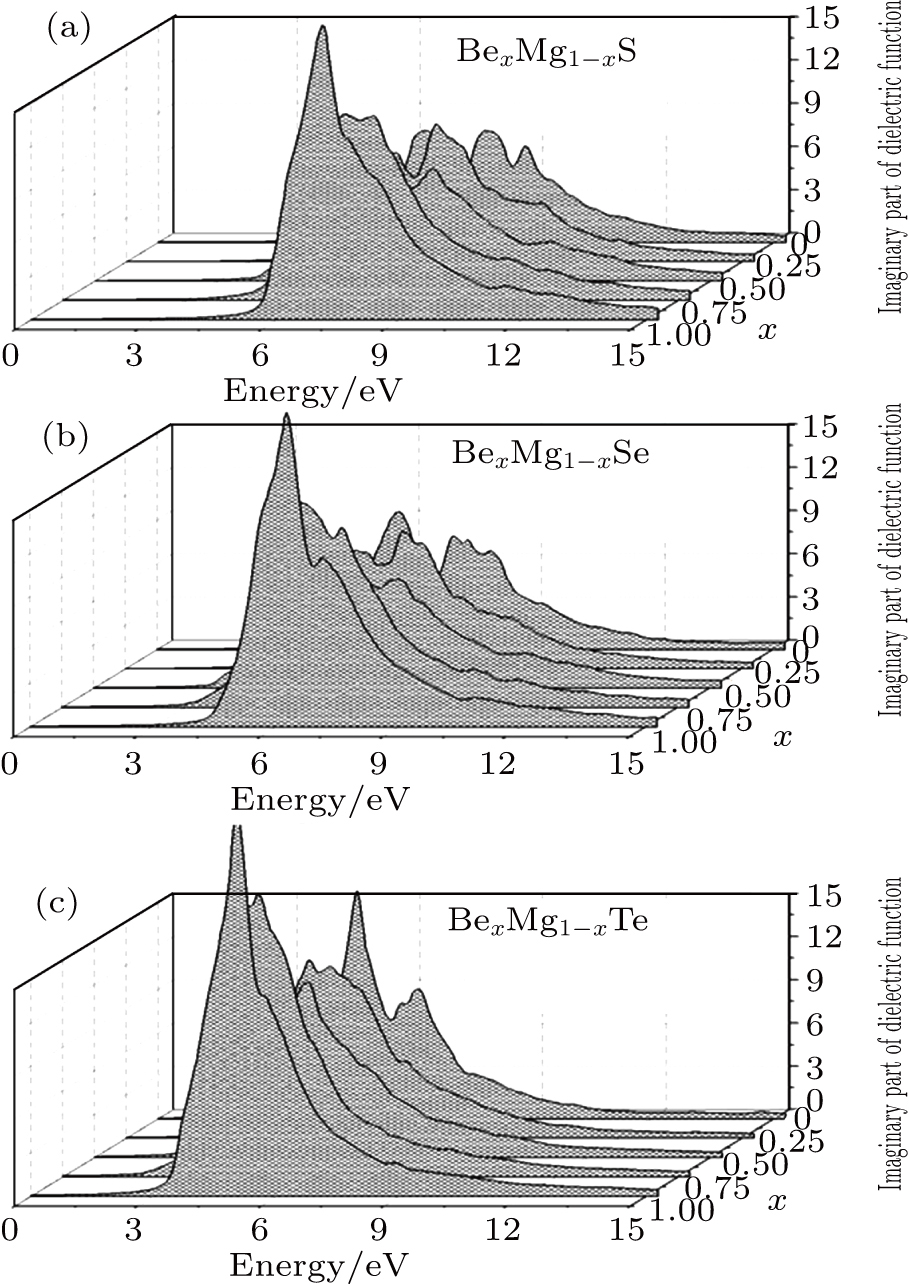 | Fig. 7. 3D plot of imaginary part of dielectric function for BexMg1−xX (X = S, Se, Te) alloys at x = 0.0, 0.25, 0.50, 0.75, and 1. |
The εreal(ω) part of DF for the binary compounds Mg-chalcogen (S, Se, and Te), Be-chalcogen (S, Se, and Te) and their corresponding ternary alloys has been computed. The quantity εreal (0), corresponding to zero frequency limits, is the electronic portion of stationary dielectric constant (DC) and found to be very important due to its connection to energy band gap such that both (εreal (0) and energy band gap) are inversely related. This feature on doping Be in Mg-chalcogen (S, Se, and Te) compounds changes significantly. Referring to Table 4 which contains the values of static DC calculated for BexMg1−xX (X = S, Se, Te) (0 < x < 1), our computed results have equitable contract with the experimental as well as additional theoretically predicted values.
The Mg chalcogenides are wide energy band gap materials attracting scientists and technologists to make their use in high temperature electronic and ultraviolet and blue-wavelength optics. On the other hand, other prime candidates for optoelectronic devices are the Be chalcogenides. Hence, an appropriate knowledge of the optical properties decides the applications of these materials in photonic industry. For the ternaries BexMg1−xX (X = S, Se, Te) in assortment 0 < x < 1, we have also calculated some other optical parameters for example refractive indices, reflectivity, absorption coefficient, and optical conductivity. For the studied alloys, only the critical transition points are listed in Table
We investigate the structural, electronic, and optical properties of BexMg1−xX (X = S, Se, Te) alloys in assortment 0 < x < 1 by employing the FP-LAPW+lo method within the framework of WC-GGA and mBJ-GGA potentials. In addition to this, the Zunger approach of special quasi-random structures (SQS) is carried out for these alloys to reproduce their disorder around the observed site of alloys in first few shells. It is noted that an excellent agreement is established between our calculated and the existing experimental values of lattice constant of the end binaries, whereas the structural parameters (lattice constant and bulk modulus) of the ternaries are found to observe the Vegard’s law. For all the ternaries and Mg chalcogenides, the computed electronic band structures predict direct energy band gaps in them except the Be chalcogenides which have indirect energy band gaps. Regarding the nature of energy band gaps in the binaries, our results are mainly consistent with the calculations based on experiments and other theoretical approaches. Furthermore, the electronic charge density maps are accomplished at revealing the charge transfer from Mg and Be atoms to the chalcogens. In the end, the optical transitions are identified with the help of critical point structure of complex DF which is frequency dependent. The present and experimental studies are found in reasonable agreement as regarding the optical parameter.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] |