† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61475029).
A new type of V-shaped photonic crystal fiber with elliptical air-holes is proposed to realize simultaneous high birefringence and nonlinearity at a wavelength of 1.55 μm. The full vector finite element method was adopted to investigate its characteristics, including birefringence, nonlinearity, and dispersion. The PCF exhibited a very high birefringence of 2.89×10−2 and very high nonlinear coefficient of 102.69 W−1⋅km−1. In particular, there were two zero-dispersion wavelengths (ZDWs) in the visible (X: 640–720 nm and Y: 730–760 nm) and near-infrared regions (X: 1050–1606 nm and Y: 850–1500 nm). The combination of high birefringence and nonlinearity allowed the PCF to maintain the polarization state and generate a broadband super continuum, with potential applications in nonlinear optics.
Owing to the design flexibility in the cross section, photonic crystal fibers (PCFs)[1,2] can be used to achieve particular properties, such as high birefringence,[3,4] high nonlinearity,[5] endless single modes,[6] and tailored dispersion.[7] PCFs with high birefringence can be used as polarization maintaining fibers (PMFs) to eliminate the effect of polarization mode dispersion (PMD)[8] or to maintain the state of polarization for the production of broadband supercontinuum (SC).[9,10] Moreover, birefringent PCFs can be applied in optical communication, optical sensing, and coherent optical communication systems. Different methods have been reported to achieve high birefringence through the destruction of symmetry, such as changing the air hole diameters along the two orthogonal directions,[11] removing several air holes in the core,[12] and introducing elliptical holes.[13,14] Large birefringences of the order of 10−3–10−2 have been demonstrated for PCFs with elliptical air holes. Issa et al.[15] have experimentally realized elliptical air-hole PCFs with birefringence of 1 × 10−4 in 2004. Li et al.[16] and Wang et al.[17] have demonstrated birefringent PCFs by combining circular and elliptical air holes, and the corresponding birefringences were 1.09 × 10−2 and 2.54 × 10−2, respectively. However, it is difficult to fabricate PCFs with both circular and elliptical air holes.
Highly birefringent PCFs with nonlinear properties have received growing attention in telecommunication and supercontinuum applications. Lee et al.[18] have experimentally demonstrated a PCF with high birefringence of the order of 10−3 and a nonlinear coefficient of 31 W−1⋅km−1 for the use of optical code-division multiple access (OCDMA) applications. Moreover, Kudlinski et al.[19] have shown that a PCF with a nonlinear coefficient of 31 W−1⋅km−1 and two zero-dispersion wavelengths (ZDWs), exhibited a higher power spectral density than that of one with a ZDW.
It is important to simultaneously obtain a high level of birefringence, large nonlinearity, and ZDWs[20] to generate the broadband supercontinuum. Ademgil et al.[21] designed a PCF with a birefringence of 2.65 × 10−2 and nonlinear coefficient of 49 W−1⋅km−1 with two ZDWs. Although Zhang et al.[22] have proposed a PCF consisting of a central defect core and cladding with elliptical air holes, that can produce a high nonlinear coefficient of 150 W−1⋅km−1, the birefringence is only 2.5 × 10−3. Recently, Rashid et al.[23] proposed an octagonal photonic crystal fiber (OPCF) to produce a large birefringence of 2.04 × 10−2 with two ZDWs in the telecommunication bands, but its nonlinearity was only 33 W−1⋅km−1.
In this paper, we designed a new type of V-shaped PCF to simultaneously achieve a high birefringence of 2.89 × 10−2 and high nonlinearity of 102.69 W−1⋅km−1 at a wavelength of 1.55 μm, as well as two ZDWs. The proposed PCF was composed of a solid silica core and cladding, with V-shaped alternating large and small elliptical air-holes. By using the full-vector finite element method (FV-FEM) with anisotropic perfectly matched layers (PMLs), the birefringence, nonlinear coefficient and dispersion were investigated.
The cross section of the designed PCF is shown in Fig.
The mode analysis was based on the cross section of the PCF structure as the wave propagated in the z direction. Figures
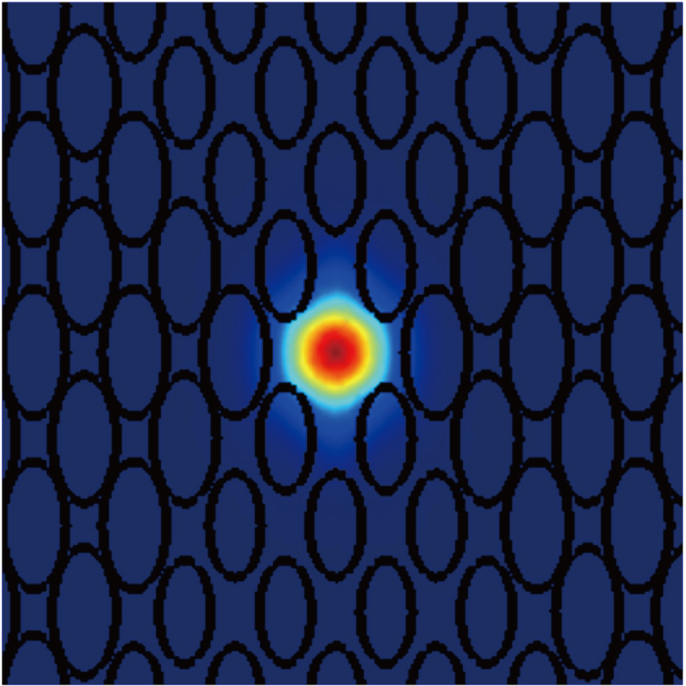 | Fig. 2. (color online) Electric field distribution of X for the polarized modes at 1550 nm with Dx = 0.64Λ, dx = 0.52Λ, Λ = 0.8 μm, and η = 0.5 |
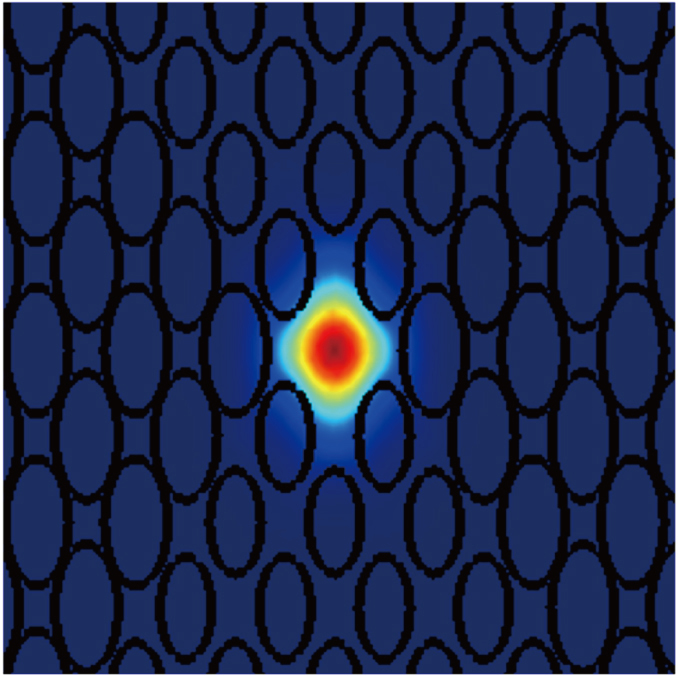 | Fig. 3. (color online) Electric field distribution of the Y polarized modes at 1550 nm with Dx = 0.64Λ, dx = 0.52Λ, Λ = 0.8 μm, and η = 0.5 |
The full vectorial finite element method (FEM) is calculated by the following equation, with a magnetic field formulation derived from the Maxwell equation
The mode birefringence is an important parameter to measure for the polarization performance of the fiber. The modal birefringence is expressed as
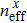

The nonlinear coefficient γ(λ) of the PCF can be calculated by
The dispersion or chromatic dispersion of the PCF consists of the material and waveguide dispersions. In general, the waveguide dispersion D(λ) depends on the effective refractive index of the fundamental mode and is given by
It is important to study the effects of the parameters on the birefringence, nonlinearity, and dispersion of the PCF. The effects of Λ on the birefringence with Dx = 0.64Λ, dx = 0.52Λ, and η = 0.5 are shown in Fig.
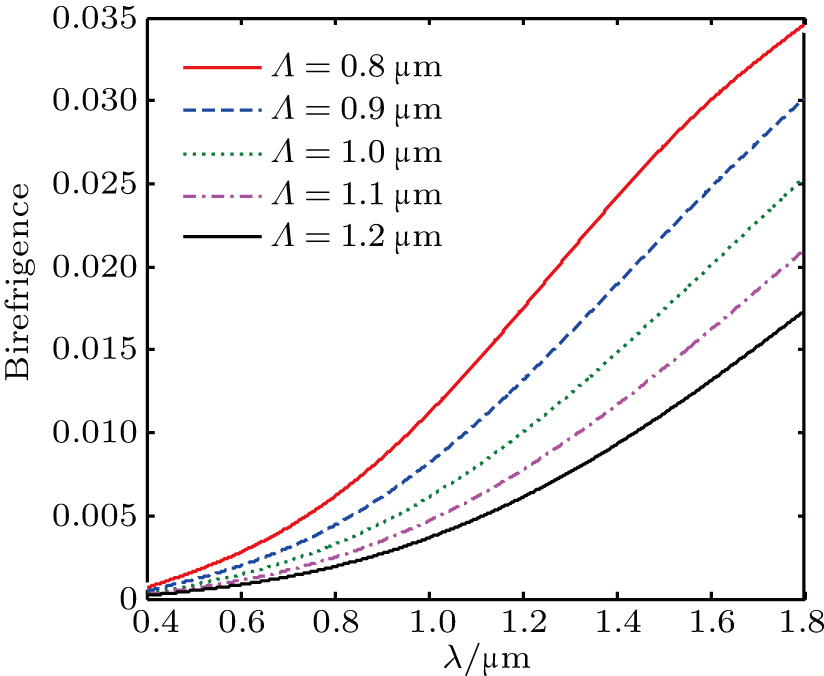 | Fig. 4. (color online) Birefringence as a function of wavelength for varying Λ with Dx = 0.64Λ, dx = 0.52Λ, and η = 0.5. |
The ellipticity has a great influence on the birefringence, as illustrated in Fig.
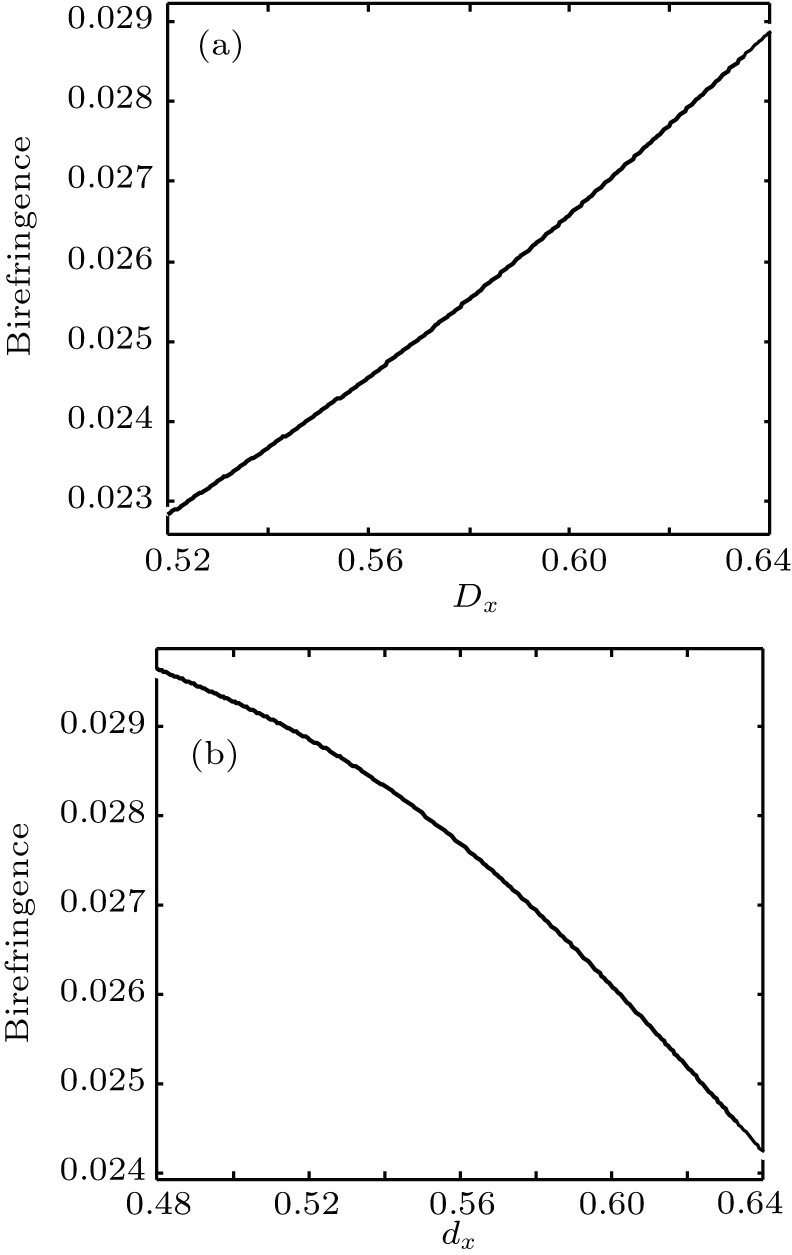 | Fig. 5. (a) Dependence of the birefringence on Dx with dx = 0.52 Λ, Λ = 0.8, and η = 0.5 at λ = 1.55 μm. (b) Dependence of birefringence on dx with Dx = 0.64Λ, Λ = 0.8, and η = 0.5 at λ = 1.55 μm |
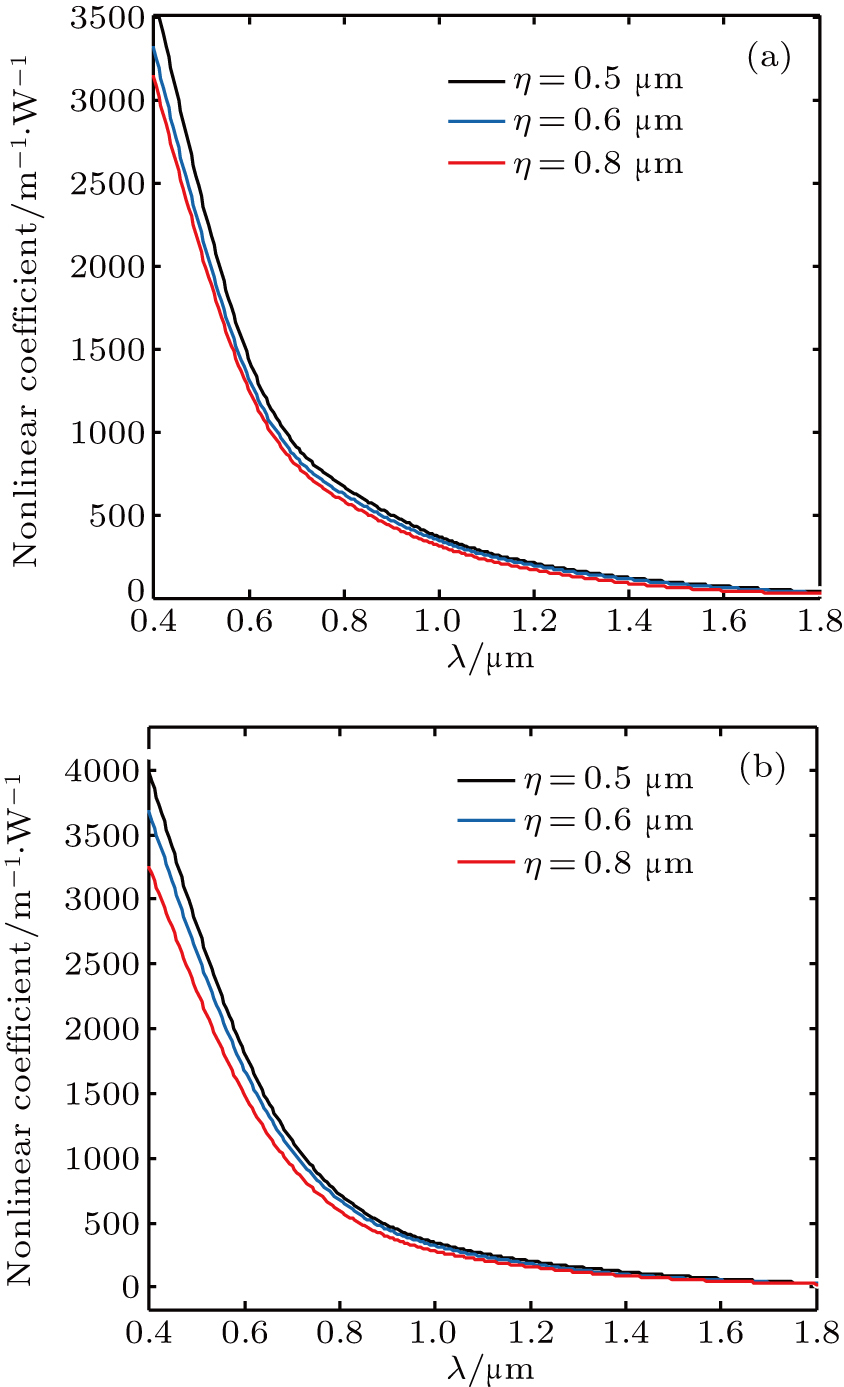
The influence of Λ on the nonlinear coefficient is given in Fig. 
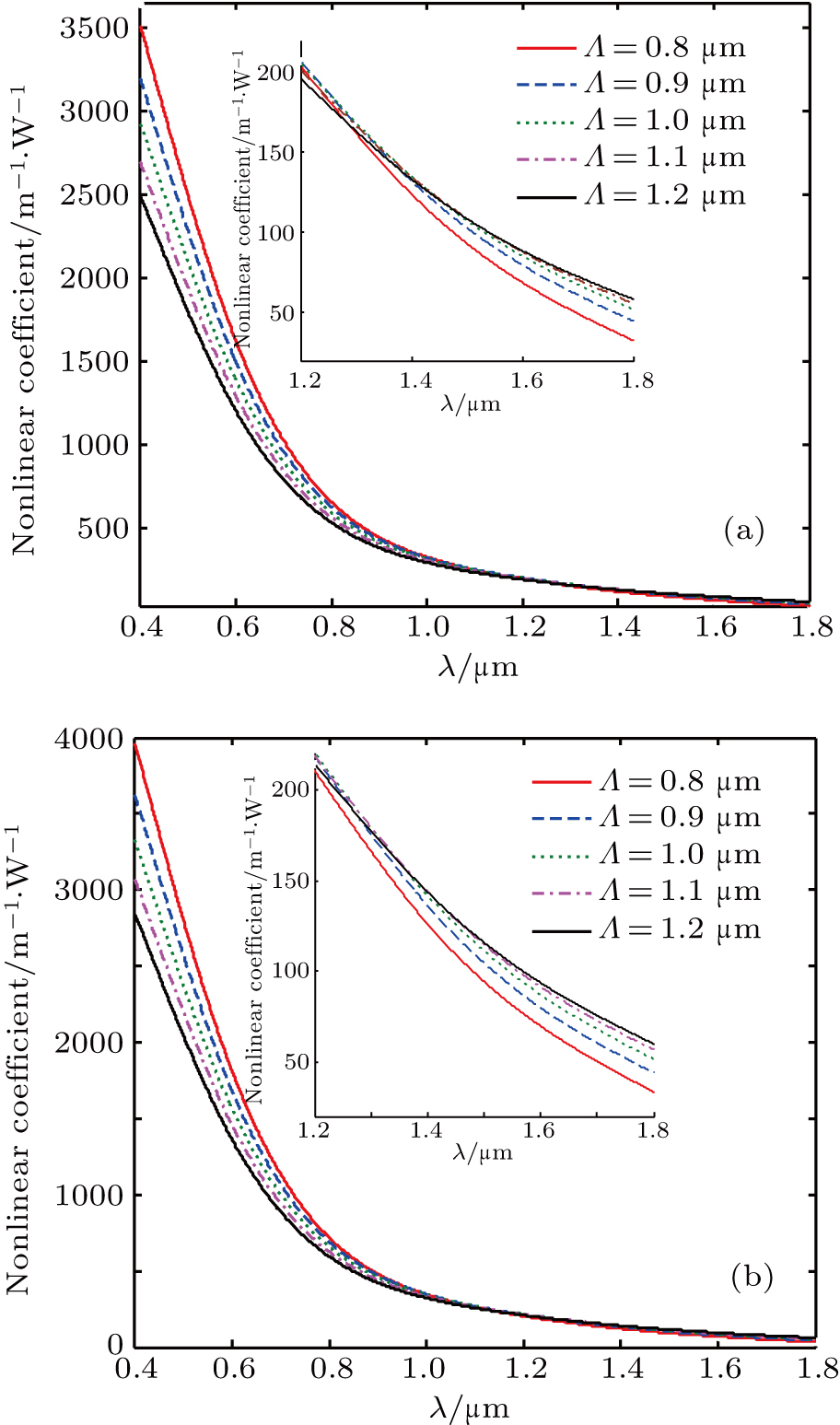 | Fig. 6. (color online) Nonlinear coefficient as a function of wavelength for different Λ with Dx = 0.64Λ, dx = 0.52 Λ, and η = 0.5 in (a) X and (b) Y polarized modes. |
When the lattice constant was increased to Λ = 1.2 μm, much higher nonlinear coefficients of 96.651 and 102.69 W−1⋅km−1 in the X and Y polarized modes, respectively, are obtained. We have listed the birefringence and nonlinearities of the proposed PCF and other PCFs designed for polarization-dependent nonlinear applications in Table
| Table 1.
Birefringence and nonlinearity of the proposed PCF and other PCFs (λ = 1550 nm). . |
The dispersion of the PCF is also investigated with the same parameters: Λ = 0.8 μm, Dx = 0.64Λ, dx = 0.52Λ, and η = 0.5, and is shown in Fig.
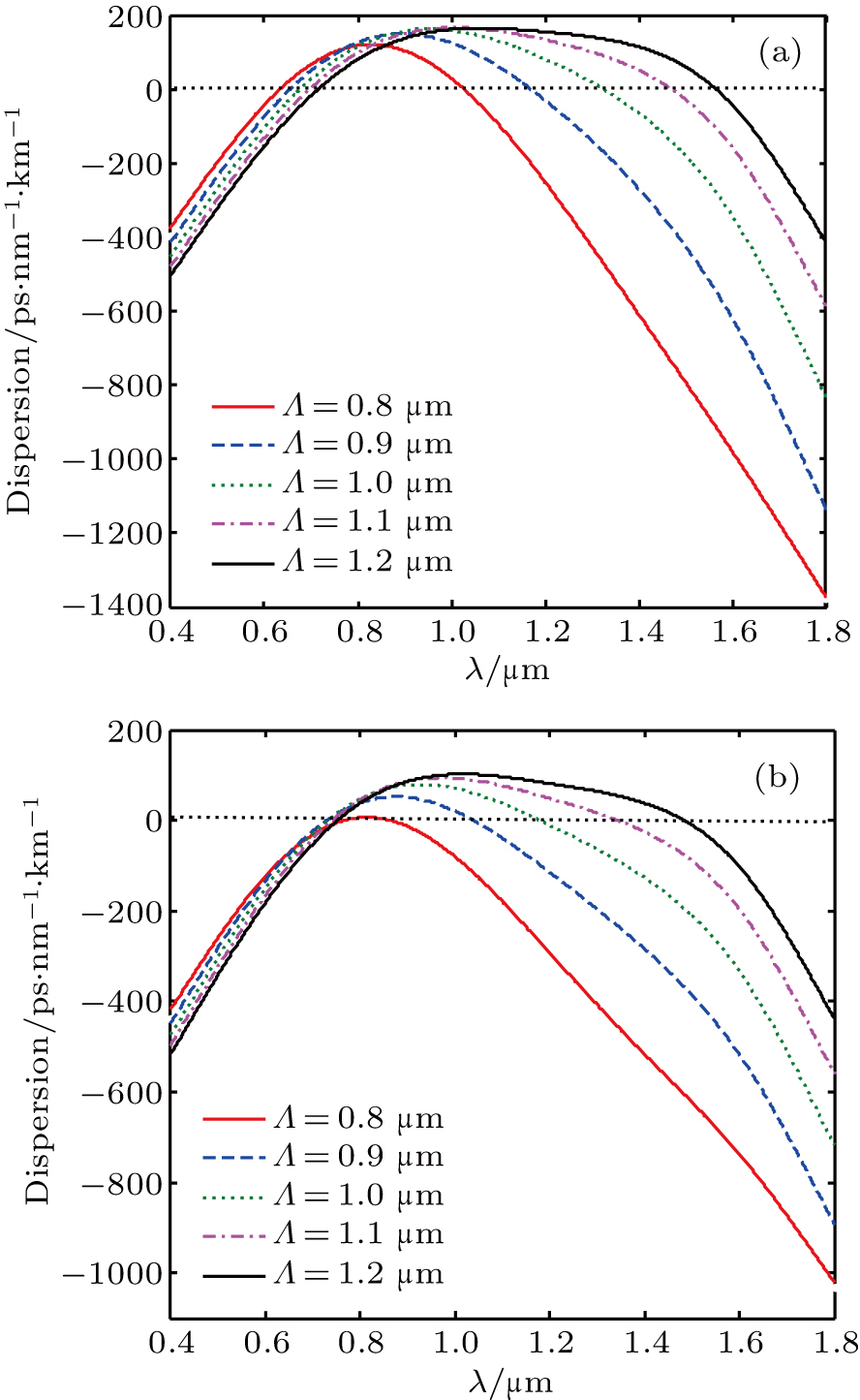 | Fig. 7. (color online) Dispersion of (a) X and (b) Y polarized modes for different Λ with Dx = 0.64Λ, dx = 0.52Λ, and η = 0.5. |
Finally, the effects of the air-hole ellipticity on the birefringence and nonlinearity were investigated by fixing Λ = 0. 8 μm, Dx = 0.64Λ and, dx = 0.52Λ, and the results are shown in Figs.
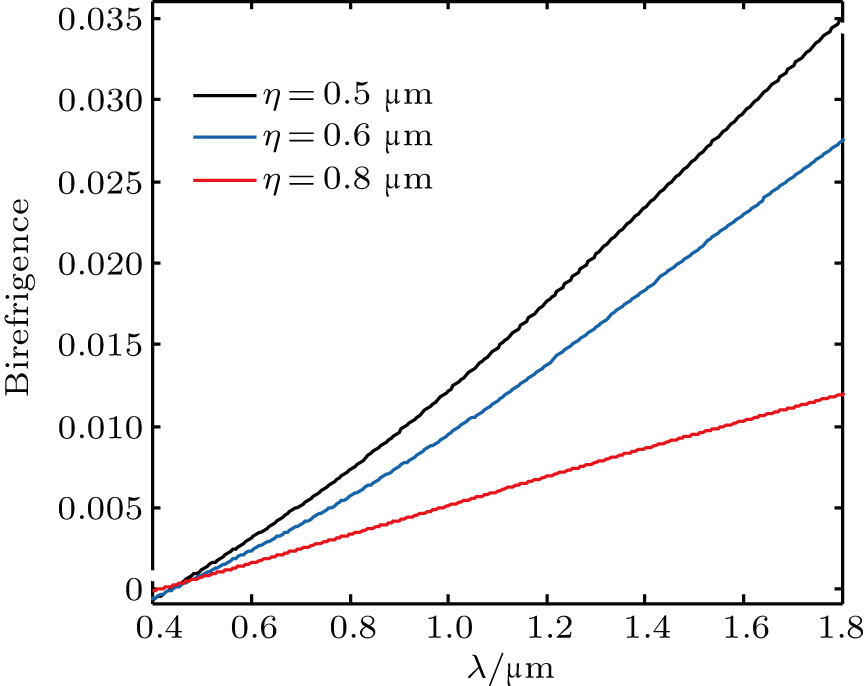 | Fig. 8. (color online) Birefringence as a function of wavelength for different η with Dx = 0.64Λ, dx = 0.52Λ, and Λ = 0.8 μm. |
Based on the full-vector finite element method with anisotropic perfect match layers, we designed a PCF that simultaneously obtained a high birefringence of 2.89 × 10−2 and nonlinear coefficient of 78.68 W−1⋅km−1 at a wavelength of 1.55 μm. In addition, two ZWDs occurred in the operation band of the Ti:sapphire oscillator (700 nm–980 nm) and C band. The useful features of simultaneous high birefringence and high nonlinearity, as well as two ZWDs, show potential for nonlinear optics applications, such as supercontinuums, four-wave-mixing, and pulse compression and reshaping.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |