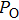
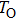
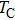
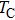
Ion channels play an important role in neuronal activities and intracellular signaling. The gating kinetics of ion channels has been extensively studied by analyzing the stochastic on/off flickering of single current traces obtained via patch clamp recording.^[1] The most basic statistical parameters measured are the open probability , and the mean open and closed times and , as well as their time distributions. Measurements of , , and in response to varying conditions such as membrane potential and ligand concentration provide an insight into channel gating mechanisms.^[2]

Typically ion channels are comprised of several subunits. For example, the voltage-dependent sodium (Na⁺) channel and potassium (K⁺) channel, the inositol 1,4,5-trisphosphate receptor (IP₃R) calcium channel, and the ryanodine receptor (RyR) calcium channel are all tetramers. Different classes of gating models have been used to incorporate the structure of tetramer ion channels: models with independent and different subunits,^[3] models with independent and identical subunits,^[4–7] and allosteric models with cooperating subunits,^[8,9] as well as the hybrid models.^[10,11]

As an important tetramer channel, IP₃R can release calcium ions (Ca²⁺) into cytosol from endoplasmic reticulum (ER) to modulate various intracellular functions. Single-channel properties of the Xenopus IP₃R channel were examined by patch clamp electrophysiology of the outer nuclear membrane of isolated oocyte nuclei, giving a biexponential distribution of open-channel dwell times with time constants of about 4 ms and 20 ms, respectively.^[12] The biexponential distribution of open time has also been observed in other channels, including the Ca²⁺ channels in the A7r5 smooth muscle-derived cell in the presence of dihydropyridine agonists,^[13] the RyR Ca²⁺ channel of skeletal muscle in the presence of bastadin 5 and bastadin 10.^[14,15]

An interesting question is the dynamics for biexponential distribution of open times of channels. The simple consideration is to directly assume two open states which determine the two exponential distributions, i.e., a short open state responding to a fast decay distribution of open times and a long open state responding to a slow decay distribution. Following this scheme, a channel model with five open states has been considered to exhibit the biexponential distribution of open times for the Ca²⁺ channels in the A7r5 smooth muscle-derived cell in the presence of dihydropyridine agonists.^[13] A different scheme for biexponential distribution of open times has been proposed in Ref. [16]. Such a channel model consists of four identical, independent subunits, each of which has only one active state. The channel opens when there are at least three subunits in the active state. The model successfully reproduces the biexponential distribution of open times.^[16,17]

In Refs. [16] and [17], the IP₃R channel consists of four identical and independent subunits, each with the 9-state. In order to discuss clearly the origin of the behavior of biexponential distribution of open times, a toy model is considered in this paper. According to the theoretical analysis and numerical simulation of the toy model, we indicate that there are two different schemes to understand the biexponential distribution. One scheme has a clear physical explanation based on an approximation process, but a better scheme is mathematically strict with little physical picture.

In the paper, we consider a toy channel model. The channel is composed of two identical and independent subunits. Each subunit has only two states: the active state (O) and the rest state (C):1 where and are transition rates between two states. The active probability ( for each subunit is then given as follows:2

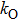
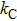
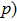
For the channel model, there are three states, i.e., CC, CO, and OO states. We assume that once there is a subunit in active state, the channel is defined as being open. So the channel states OO and CO are open states, while the channel state CC is a closed state. Accordingly, the three channel states have the following transition processes:3

To consider dimensionless unit by assuming , we have . In other words,

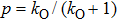
Thus in the model, we have only one free parameter p which is the active probability of the subunit. So the channel model can be rewritten as4

As a result, the channel open probability is expressed as^[12]5 with the mean open time and the mean closed time with the flux .

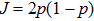
In the following, we use the generator matrix theory^[16,18,19] to discuss the open-time distribution of the channel. Assuming that the probabilities in the states of CC, CO and OO are C, O₁, and O₂, respectively, the binding-unbinding reaction equations of the channel are given by6 Thus the generator matrix is given as follows:7 With the generator matrix, we have the following open matrix:8 and thus the open-time distribution is defined as9

Considering the definition of the exponent of a matrix, with the open-time distribution is then given by10 with and Substituting and A into , the open-time distribution becomes11

Let and then we will have12 Let13 14 and so then the open-time distribution will be expressed as15

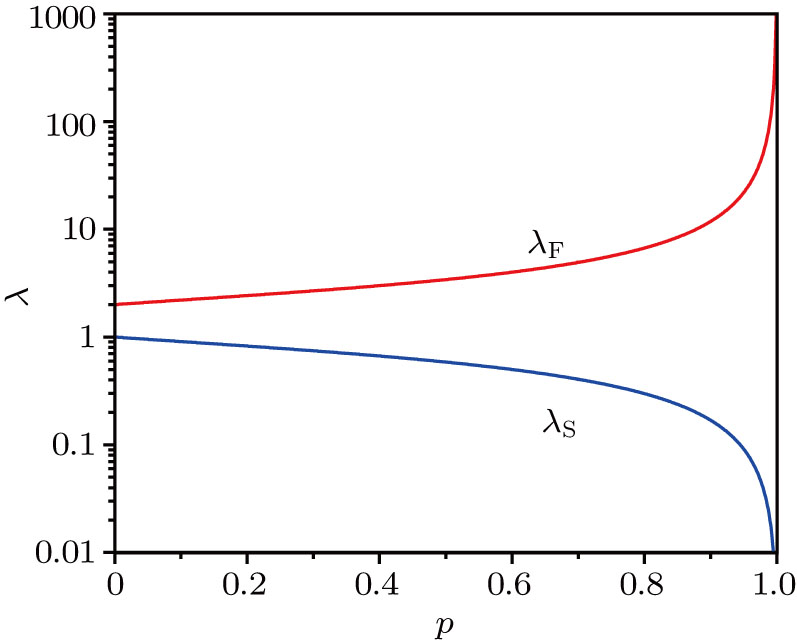
As a result, the expression given in Eq. (13) indicates that the open-time distribution consists of two exponential decay modes, i.e.,16 with having a slow exponential decay rate :17 and having a fast exponential decay rate :18

One property of the open-time distribution is that the total open-time distribution should be unity. In order to check it, we consider the integral as follows:19 with Then we have20 Because as expected, the total probability is then given as .

Figure 1 shows the open-time distributions at p = 0.1 and 0.9, which are calculated according to Eq. (15). The fast and slow decay distributions of open times, i.e., and are also plotted in the figure. The open-time distribution can be strictly separated into two exponential distributions. With a large p, the double exponential distribution of open times can be clearly observed in the curve of the open-time distribution as shown in Fig. 1(b), including the fast decay mode for the short time duration and the slow decay mode for the long time duration.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Open-time distributions at p = 0.1 (a) and 0.9 (b). The upper, middle and lower panels give the total, the fast decay, and the slow decay distributions of open times, respectively. In the model, the time has a dimensionless unit.

Figure 2 shows the plots of the two exponential decay rates versus p given by Eqs. (13) and (14). With increasing p, the decay of the fast decay mode becomes faster, while the decay of the slow decay mode becomes slower. In detail, with p increasing from 0 to 1, the fast decay rate increases from 2 to infinity, while the slow decay rate decreases from 1 to 0. Especially, with p approaching to 1, is close to 0 and so one can typically observe the slow decay distribution almost parallel to the x axis.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Two exponential decay rates versus p, obtained in theory.

Figure 3 depicts the contribution percentages of fast decay and slow decay modes with respect to the open-time distribution, which are defined by Eqs. (17) and (18) divided by Eq. (16), respectively. Figure 3 indicates that the slow decay mode typically occupies the majority among the open time series, just because it decays slowly. A surprising observation is that both the fast decay and slow decay modes contribute to the open time series in a nonlinear manner with increasing p. With p approaching to 0 and 1, almost all the open time events are the slow decay mode. With p approaching to 0.5 from both values of p = 0 and 1, the contribution of fast decay mode to the open time series keeps increasing. However, the largest percentage that the fast decay mode contributes to the open time events is still less than 15% at p = 0.5.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Contribution percentages of (a) fast decay mode and (b) slow decay mode to the open-time distribution.

Now we carry out the numerical simulation to discuss the open-time distribution of the channel model. As a result, the stochastic simulation of the detailed transition process between active and rest states of each subunit is recorded to obtain the stochastic time series of channel open and closed states. Different approaches have been suggested to simulate the stochastic channel dynamics.^[20–22] In the paper, we directly simulate the stochastic dynamics of the channel model by a two-state Markovian process.^[5,23,24] In detail, the state of each subunit is updated in small time steps of . If the subunit is, for example, in rest state at time t, then at time , it can go to the active state with the transition probability , otherwise it will remain in the rest state. In the simulation, a random number homogeneously distributed in [0,1] is generated at each time step and compared with the transition probability in order to determine which state the channel subunit will be at the next time step. With such a Markovian simulation, one can trace the subunit state, as well as the channel state, with time in detail.

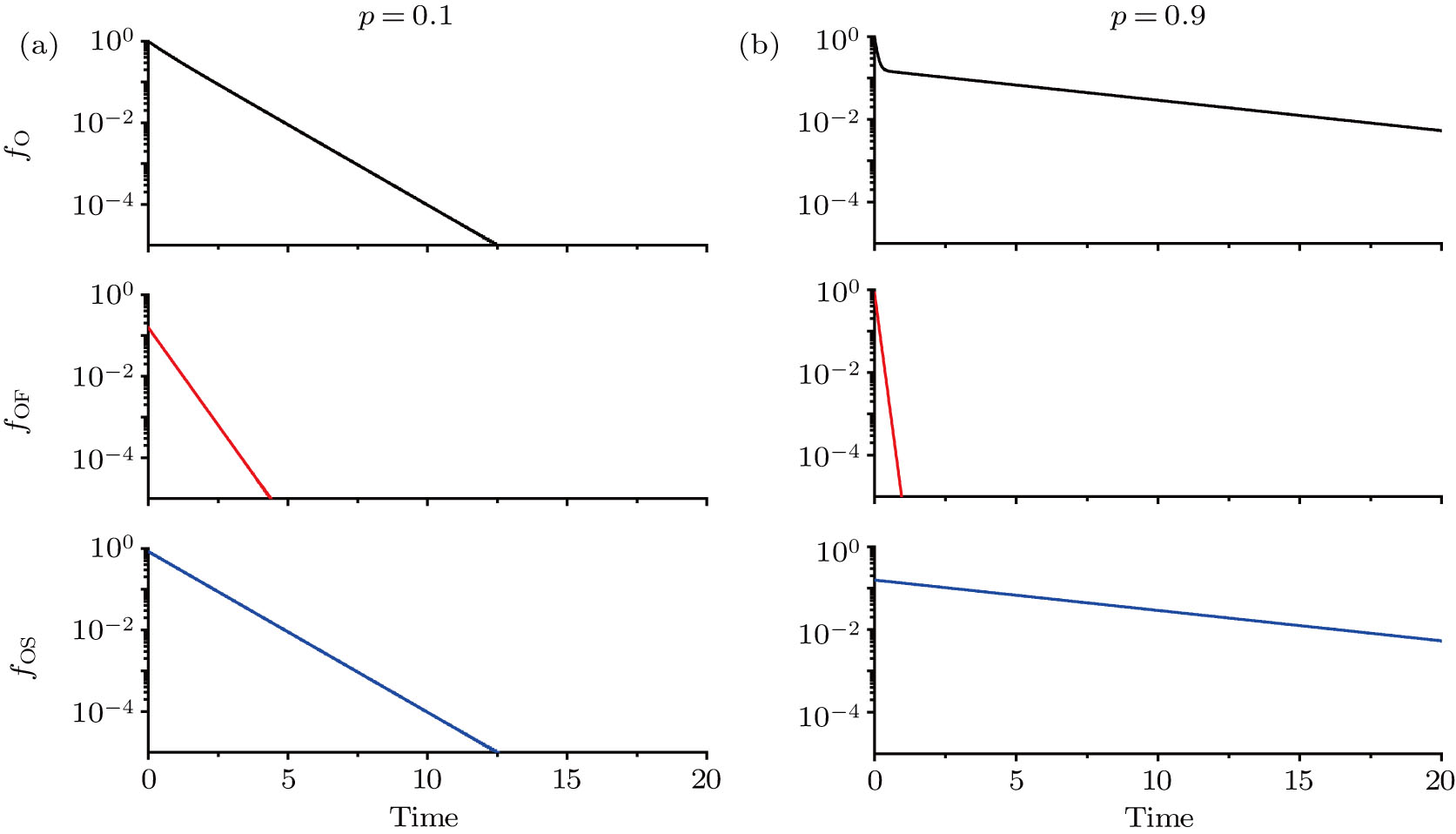
In the following, by discussing the Markovian numerical simulation, we provide another scheme to understand the biexponential distribution of open times. Figure 4 shows the variations of channel state and the number of active subunit with time at p = 0.5. As defined, once there is a subunit in the active state, the channel becomes open. So we can distinguish between two types of channel open states: the CO-only open state and OO-related open state.^[16] Here the CO-only open state is defined as that involving only one subunit in active state in the whole duration of the opening, whereas the OO-related open state involves at least one occurrence of two subunits in the active state. Examples for the CO-only and OO-related open states are marked by arrows in Fig. 4.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) Variations of (a) channel state and (b) the number of active subunits with time at p = 0.5. The channel open state can be classified as the CO-only and OO-related open states as marked by arrows.

With the trajectories of channel open and close states, we can calculate the open time distribution. As examples, the open-time distributions at p = 0.1, 0.5, and 0.9 obtained with Markovian simulation are plotted in Fig. 5, which are the same as those given in Fig. 1.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Open-time distributions at p = 0.1 (a), 0.5 (b), and 0.9 (c), obtained with Markovian simulation.

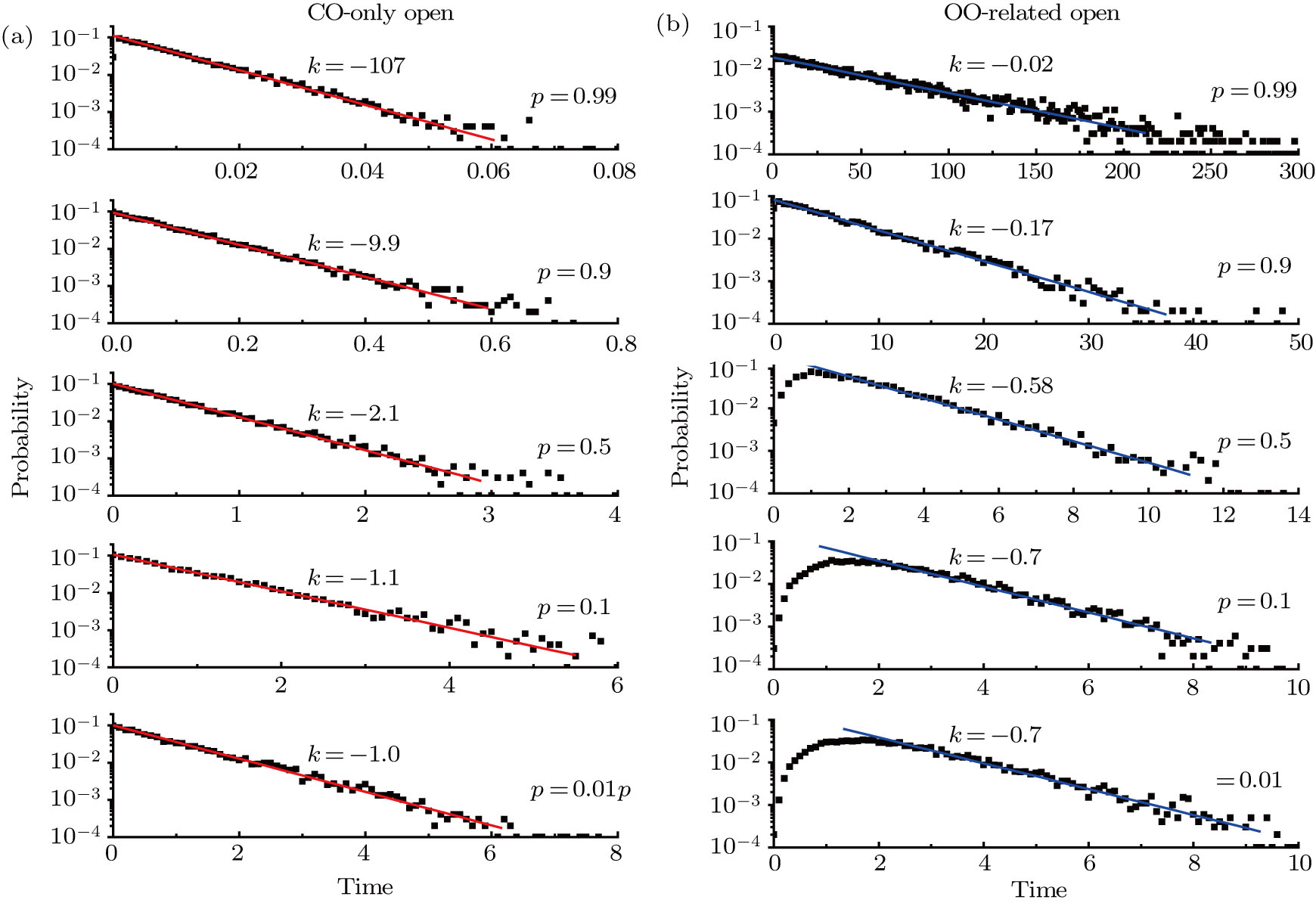
Because the channel open states can be distinguished as the CO-only and OO-related open states, the open time series can then be split into the CO-only and OO-related open modes. The distributions of the CO-only and OO-related open time events are given in Figs. 6(a) and 6(b), respectively. One can see that the CO-only open-time distributions typically show an exponential decay with time. However, the OO-related open-time distributions exhibit an increase in a small time interval, and then a decrease at large time duration. Because the OO-related open-time distribution is not strictly an exponential curve, the exponential fitting is only carried out in the region of large time duration as shown in Fig. 6(b).

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) Distributions of (a) CO-only open events and (b) OO-related open events at p = 0.99, 0.9, 0.5, 0.1, and 0.01 from upper to lower panels. The values of decay rate k fitted with the exponential function are also given in each sub-figure.

By fitting the exponential decays of CO-only and OO-related open-time distributions, the exponential decay rates can be obtained. The decay rates for both the CO-only and OO-related open states against p are given in Fig. 7. The OO-related open events are a slow decay mode, while the CO-only open events are a fast decay mode. Around p = 0.01, the decay rate of OO-related open mode is about 0.74, and the decay rate of CO-only open mode is about 1.0. With p increasing from 0.01 to 0.99, the decay rate of CO-only open mode increases from 1 to 107, while the decay rate of OO-related open mode decreases from 0.7 to 0.02.

Fig. 7.

	Figure Option ViewDownloadNew Window
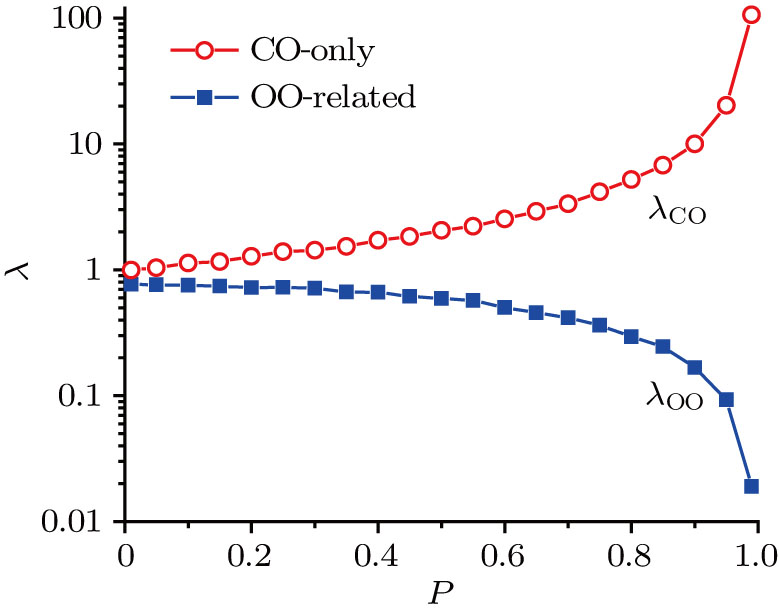	Fig. 7. (color online) Exponential decay rates of the CO-only and OO-related open-time distribution versus p.

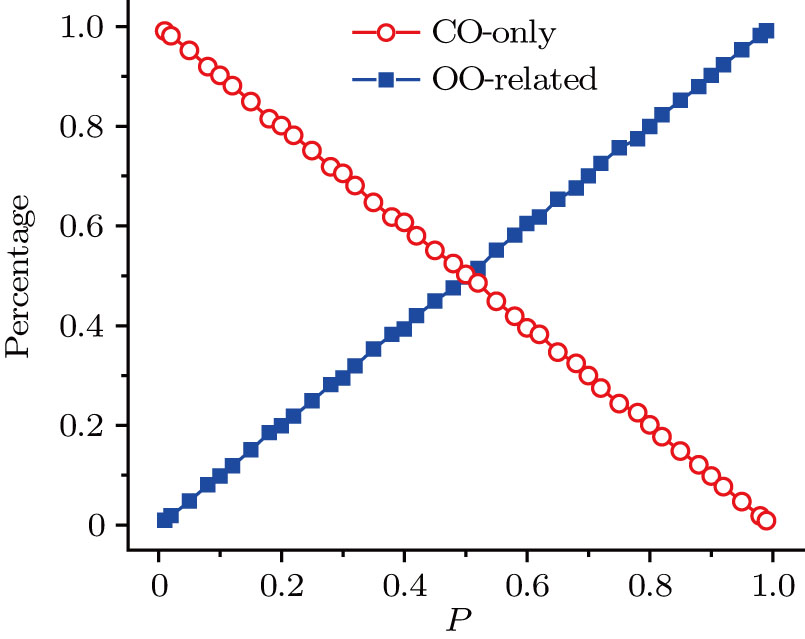
By counting the numbers of CO-only and OO-related open events of the open time series, the contribution percentages of CO-only and OO-related open modes as a function of p can be calculated as given in Fig. 8. A linear increasing curve with slope k = 1 is observed for the contribution percentage of the OO-related open mode. As a result, with p approaching to 0, one can typically find CO-only open events, and the OO-related open mode is hardly observed; while with p approaching to 1, one can typically find OO-related open events, and the CO-only open model is hardly observed. At p = 0.5, there is an equal chance to observe the CO-only and OO-related open events.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. (color online) Plots of contribution percentage of CO-only and OO-related open modes versus p.

In this paper, we consider a toy model to discuss the behavior of the biexponential distribution of open times, which has been observed in various types of channels.^[12–15] The toy channel consists of two identical and independent subunits. Each subunit has only an active state and a rest state. The channel opens when at least one subunit is in active state. The open time distribution of the channel is investigated systematically with theoretical analysis and Markovian simulation. We show that there are two different schemes to understand the biexponential distribution of open times.

First we use the generator matrix theory^[16,18,19] to discuss the open-time distribution. Mathematically strict results are derived, but with little physical picture to understand clearly what open time events are fast and slow decay modes. The biexponential distribution of open times actually originates from 2 by 2 square open matrix, due to the two open states of CO and CC. As a result, the expression of open-time distribution consists of two exponential decay modes: one with a slow decay rate and the other with a fast decay rate. A surprising observation is that the fast and slow decay modes contribute to the open time series in a nonlinear manner with increasing p. The largest percentage that the fast decay contributes to the open time series at p = 0.5 is still less than 15%.

Another scheme on open-time distribution has a clear physical explanation, but based on an approximation process for the fitting of exponential distribution. Because the channel has two open states, i.e., CO-only and OO-related open states, the open time events can then be split into the CO-only and OO-related open modes. Linearly increasing and decreasing curves are observed for contribution percentages of OO-related and CO-only open modes, respectively. Especially, at p = 0.5, the CO-only and OO-related open states each contribute 50% probability to the open time events.

As a result, the two different schemes reveal different characteristics of the open times of the channel model. The scheme with the classification of CO-only and OO-related open states is easily understandable with a clear physical picture, which has been used to discuss the behavior of the open time distribution of the IP₃R channel model based on the numerical simulation of stochastic channel dynamics.^[16,17] Compared with the toy model discussed here, the biologically realistic IP₃R channel model is complex. Thus it is a little hard to use the generator matrix theory to investigate the open-time distribution of the IP₃R channel model. However, in the present paper our comparison results suggest that the analytic discussion with the strict generator matrix theory should be considered in order to understand the behaviors of multiple exponential distributions of open times of biological channels, such as the IP₃R channel, which are typically complex.