† Corresponding author. E-mail:
Project supported by the Scientific Research Foundation of the National Natural Science Foundation of China–Outstanding Youth Foundation (Grant No. 51622906), the National Natural Science Foundation of China (Grant No. 51479173), the Fundamental Research Funds for the Central Universities, China (Grant No. 201304030577), the Scientific Research Funds of Northwest A & F University, China (Grant No. 2013BSJJ095), the Science Fund for Excellent Young Scholars from Northwest A & F University (Grant No. Z109021515), and the Shaanxi Provincial Nova Program, China (Grant No. 2016KJXX-55).
A fast-slow coupled model of the hydro-turbine governing system (HTGS) is established by introducing frequency disturbance in this paper. Based on the proposed model, the performances of two time scales for bursting oscillations in the HTGS are investigated and the effect of periodic excitation of frequency disturbance is analyzed by using the bifurcation diagrams, time waveforms and phase portraits. We find that stability and operational characteristics of the HTGS change with the value of system parameter kd. Furthermore, the comparative analyses for the effect of the bursting oscillations on the system with different amplitudes of the periodic excitation a are carried out. Meanwhile, we obtain that the relative deviation of the mechanical torque mt rises with the increase of a. These methods and results of the study, combined with the performance of two time scales and the fast-slow coupled engineering model, provide some theoretical bases for investigating interesting physical phenomena of the engineering system.
The multi time-scale phenomenon which results from the actual time effect, spatial effect, structural effect and physical effect in a real system, exists in many complex mathematical models.[1–3] The complex mathematical model in which the state variables have very different changing rates is called the fast-slow coupled model.[4–8] The response of a fast-slow coupled system is performed by the alternate change of large amplitude oscillation (i.e, spiking state) and micro amplitude oscillation (i.e, quiescent state). The time history and the trajectory connecting the two special behavior process are referred to as bursting oscillations.[9–11]
Multi time-scale dynamics can reveal nonlinear essential characteristics of the system from the dynamic point of view, and it is extensively used in biology, chemistry, life sciences, physics, etc.[12–17] For example, Gu et al.[18] not only revealed the nonlinear dynamics of the firing patterns of neural pacemakers but also provided experimental evidence for the existence of bifurcations from bursting to spiking simulated by using the theoretical models. Song and Xu[19] showed that the time delay must be large enough for bursting behavior to occur in a delayed system and the different bursting behaviors are related to the delay coupling and external inputs. Ji and Bi[20] found that the multiple crossing bifurcation, which is the combination of the Hopf bifurcation and the turning point bifurcation and occurs at the non-smooth boundaries, causes the periodic buster to the quasi-periodic oscillation. Guo et al.[21] investigated how intrinsic channel noise affects the response of stochastic Hodgkin–Huxley neuron to external fluctuating inputs with different amplitudes and correlation times. Hou et al.[22] investigated the fractional-order Belousov–Zhabotinsky (BZ) reaction with different time scales and studied the slow-fast effect in fractional-order BZ reaction with two time scales coupled.
As is well known, few researchers concentrate on modeling and analyzing the fast-slow coupled engineering system such as the HTGS. The HTGS is a complex nonlinear, time-variant and non-minimum phase system involving hydro dynamics, mechanical dynamics, and electrical dynamics. From the point of view of dynamically coupled hydraulic-mechanical-electric-structural system for a hydropower station, the parameters in the HTGS can be divided into a fast transmission rate (electrical transient) and slow strain rate (hydraulic transient).[23,24] In recent years, achievements about modeling and controlling of the HTGS are becoming more and more abundant. For example, Zhang et al.[25] and Li et al.[26–28] concentrated on the modeling and analyzing of the HTGS in the process of large fluctuation. Zeng et al.[29] and Xu et al.[30] focused on Hamiltonian mathematical modeling of HTGS which can be used to describe general open systems with the structure of energy dissipation and the exchange of energy with the environment. Pico et al.[31] presented an investigation of hydro power plants with pelton-type turbine-generator sets and robust control theory was used to design a hydro-stabilizer. Salhi et al.[32] stated an approach to modeling and controlling a micro hydro power plant considered as a non-linear system by using a Takagi–Sugeno fuzzy system. Husek[33] presented a proportional-integral-derivative controller design for hydraulic turbine based on sensitivity margin specifications. These research results not only explain many complex phenomena in the actual operation of the hydropower station, but also provide a theoretical basis for the safe and stable operation of the hydropower station system. Although great achievements have been made in autonomous HTGS with single time scale, many time-relative non-autonomous factors existing in the real HTGS with multi time-scale have not been considered carefully. Some complex disturbances that are defined as risks constantly occur in the process of operation of the HTGS, like the load disturbance, the frequency disturbance, and the flow rates disturbance.[34] Besides, the non-autonomous factors not only change the structure of the HTGS, but also make the system more complex. Therefore, it is necessary to study the non-autonomous HTGS with multi time-scale, which will provide a theoretical basis for studying the operation stability and control strategy for the system.
In this paper, a mathematical model of the non-autonomous HTGS with two time scales is proposed by introducing frequency disturbance as periodic excitation. Next, compared with the traditional model of HTGS, the stabilities and dynamic behaviors of the mathematic model of non-autonomous HTGS with two time scales are investigated by numerical simulation. Besides, combining the time waveforms and the phase portraits, the phenomena of the bursting oscillations are described in detail. At the same time, the bursting oscillations of the system, with different amplitudes of periodic excitation, are analyzed by numerical simulation. Finally, the conclusions of this study and discussion about future work are presented.
The rest of the paper is organized as follows. In Section
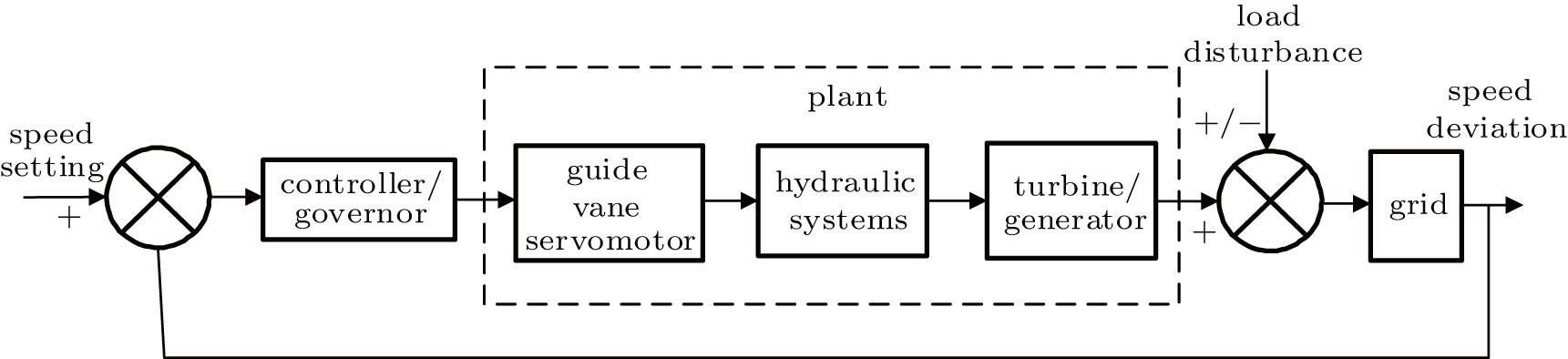
As shown in Fig.
The dynamic characteristics of generator and load can be described by[23,36]
The dynamic model of the hydro-turbine and hydraulic systems can be expressed as[37]
The speed governor is composed of a controller and a guide vane servomotor. The output signal of the PID controller can be written as[25,27]
The dynamic characteristics of a guide vane servomotor[28] can be described as
Based on the modular modeling method,[24–28,36] a traditional mathematical model of the autonomous HTGS with single time scale can be described as follows:
There are many time-relative non-autonomous factors in the real HTGS, such as the frequency disturbance in the operation process of the hydropower station. Generally, the frequency disturbance in the system is caused by the fluctuation of grid load with the change of time.[37,38] Here, we consider the frequency disturbance of the HTGS as a periodic excitation. We set this periodic excitation as xs, and xs = a sin ωt, where a and ω are respectively the amplitude and the frequency of the periodic excitation. Thus, a mathematical model of the HTGS with the periodic excitation is obtained as
In this paper, the value of the periodic excitation frequency ω is selected as 104, which can be treated as a parameter of fast transmission rate. That is to say, the frequency of the periodic excitation is far greater than that in the traditional system. Thus, a model of the non-autonomous HTGS with two time scales is established by selecting an appropriate value of periodic excitation frequency.
In this section, a traditional model and a fast–slow coupled model of the HTGS are used to study the dynamical characteristics of the HTGS with two time scales. Here, the numerical simulations are carried out by using the Runge–Kutta method. Specifically, the initial values of [
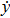
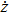
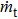
| Table 1.
Values of HTGS parameters. . |
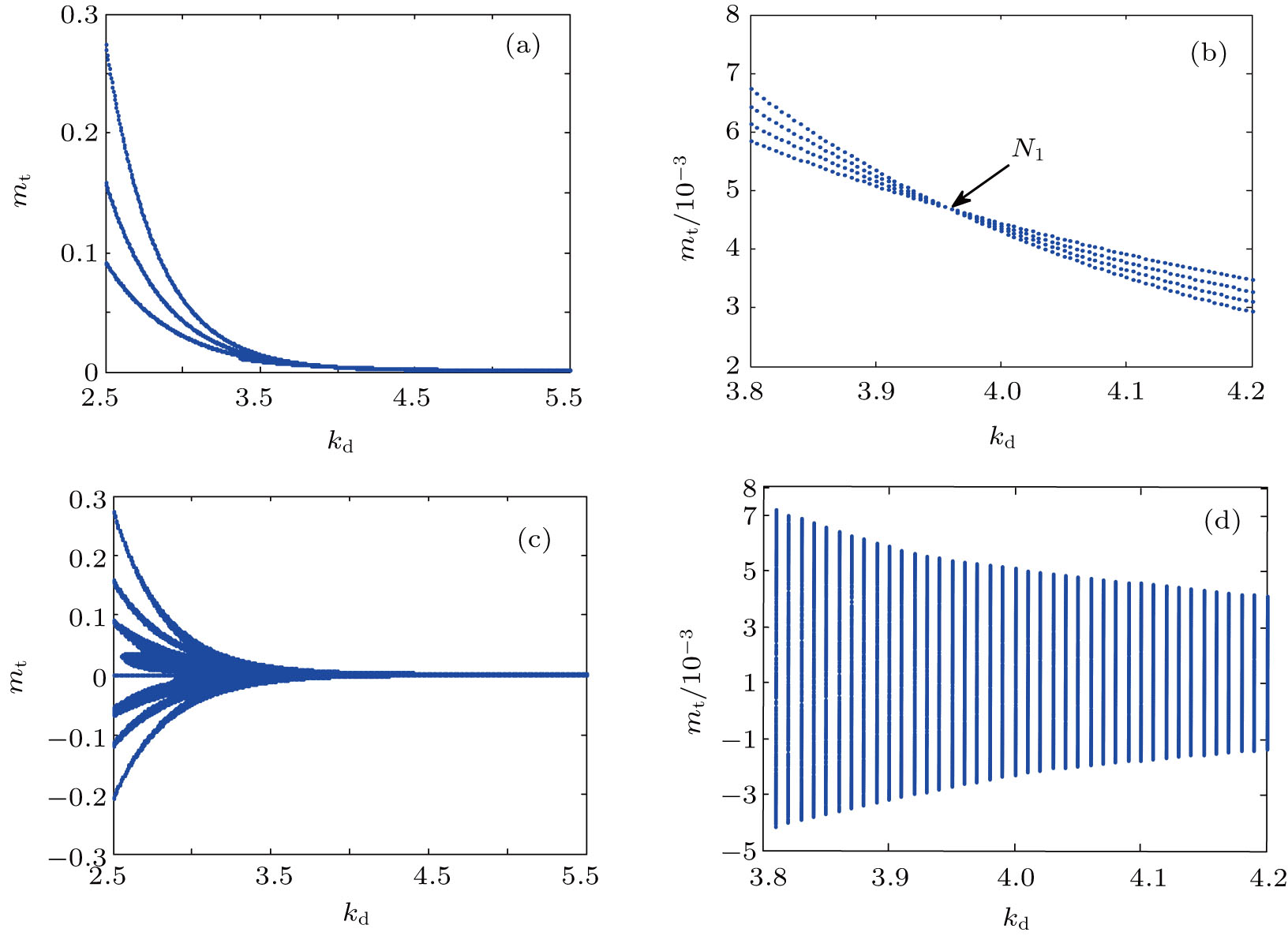
Bifurcation diagrams of the mechanical torque mt with respect to the governor parameter kd are presented in Fig.
From Figs.
Figures
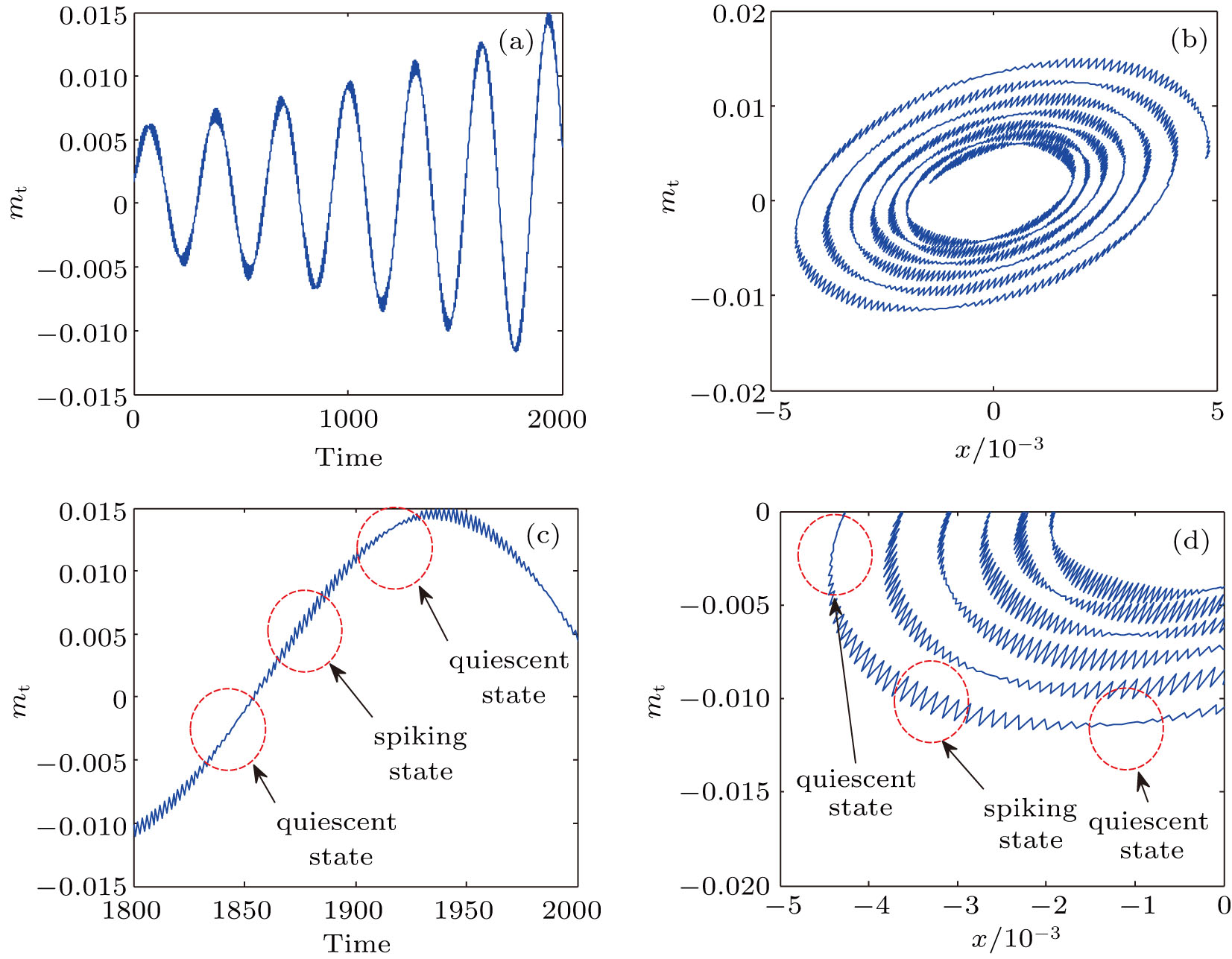
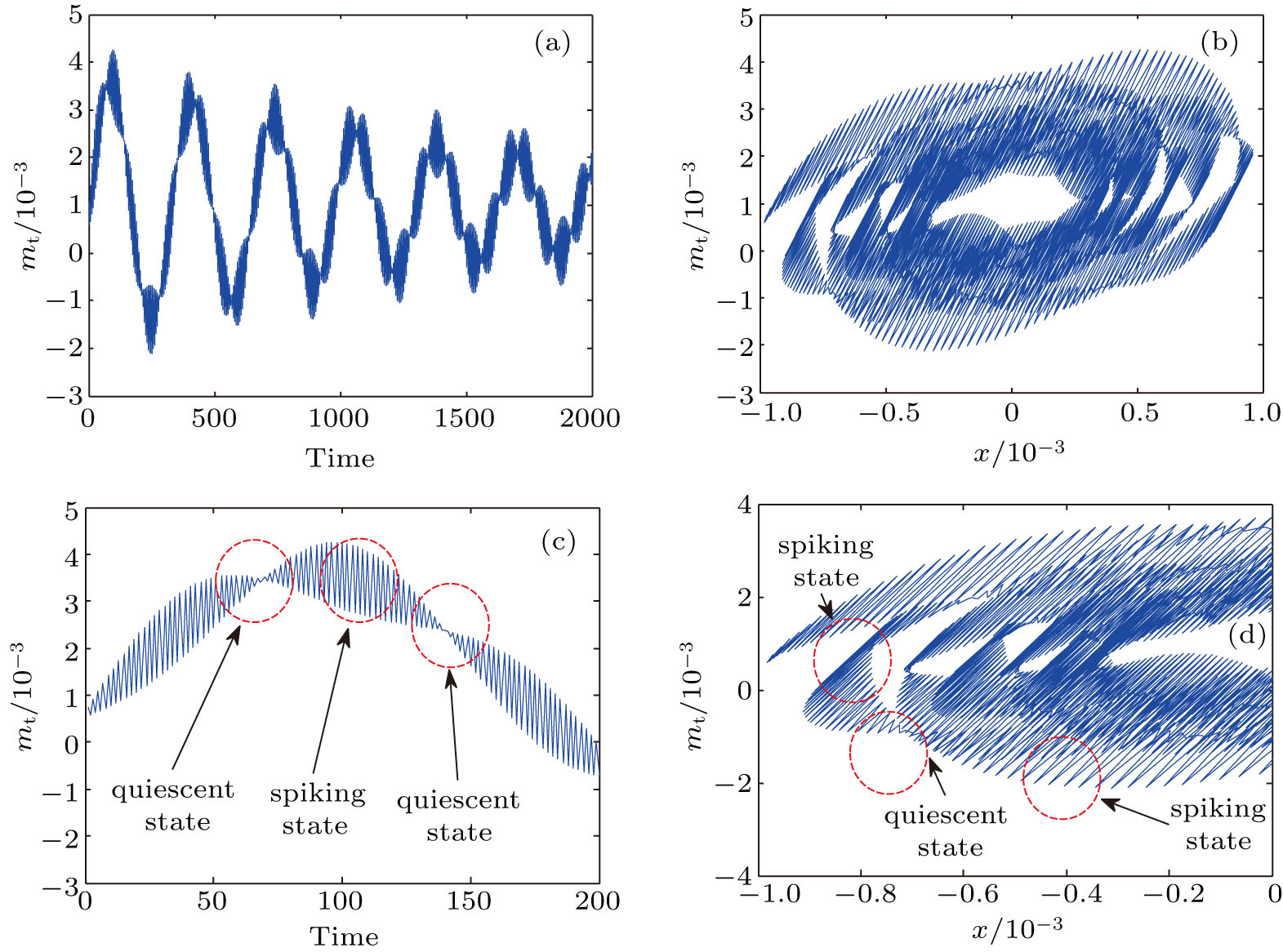
In order to further study the dynamical behaviors of the system with two time scales, we select three typical points in Fig.
For kd = 3.5, as shown in Fig.
Figure
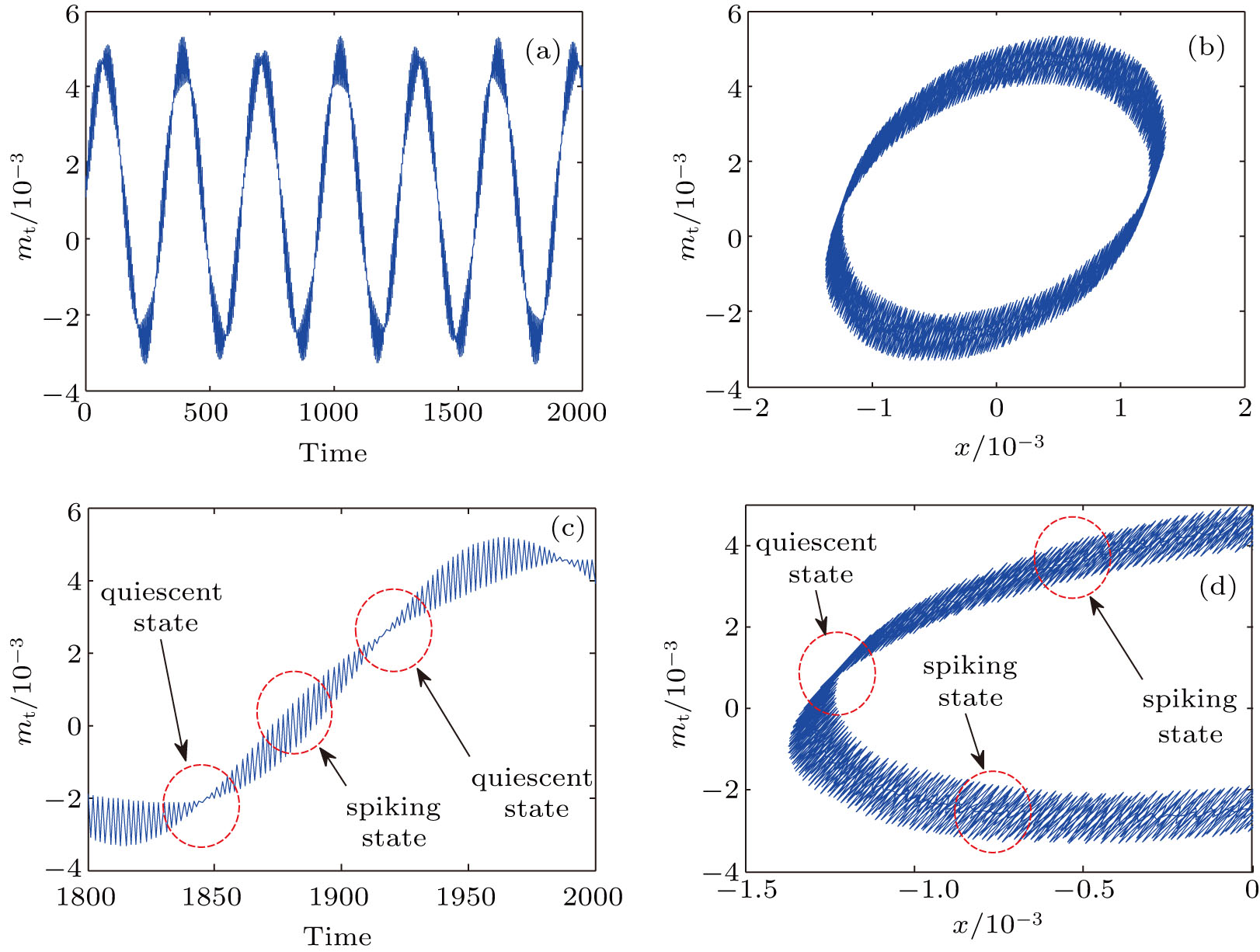
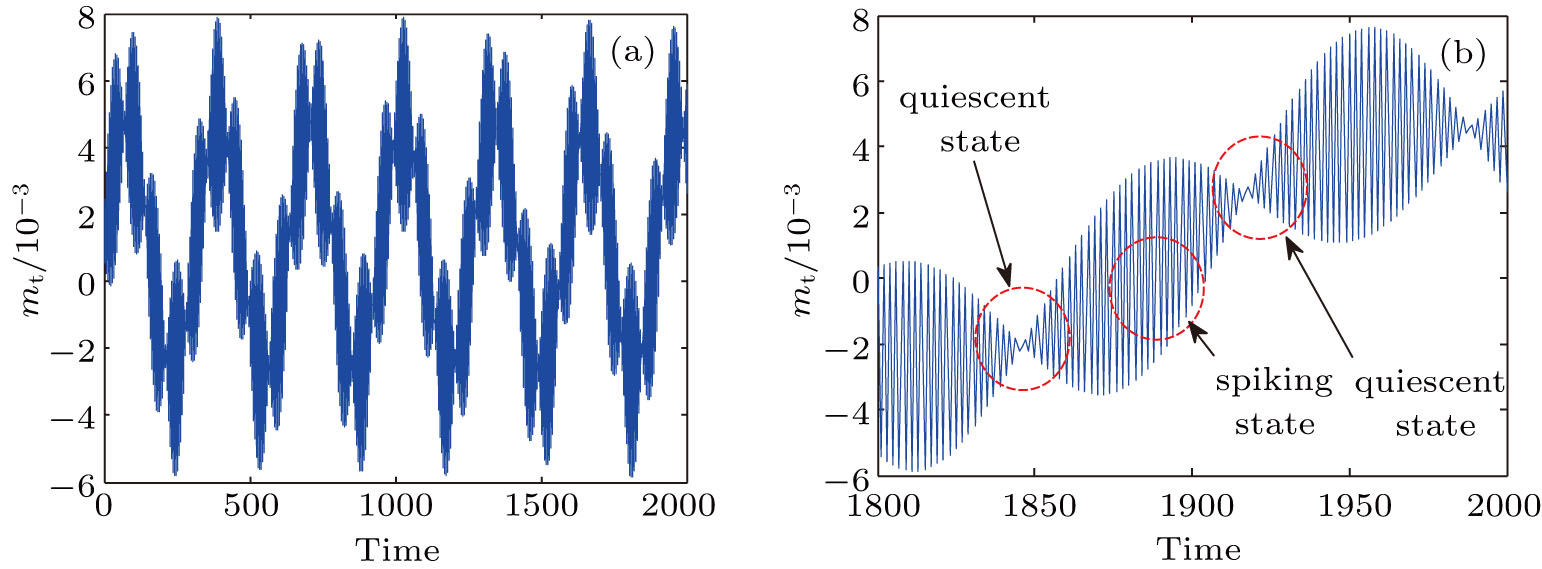
The responses of the HTGS with kd = 4.5 are shown in Fig.
In order to reveal the bursting oscillation of the system with the amplitude of the periodic excitation, time waveforms and phase orbits are presented with different values of the amplitude of the periodic excitation a at kd = 3.96, namely a = 0.00, a = 0.001, a = 0.005, and a = 0.01.
The value of the amplitude of the periodic excitation is equal to 0.00, which means that the frequency disturbance does not occur in the operation process of the hydropower station. For a = 0.00, as shown in Fig.
These results show that the amplitude of the periodic excitation has a great influence on the dynamic behaviors of the system. As the value of the amplitude of the periodic excitation a increases, the effect of the bursting oscillations on the system becomes stronger.
The HTGS is a complex nonlinear, time-varying, and non-minimum phase system involving hydro dynamics, mechanical dynamics, and electrical dynamics, which is accurately a multi-time-scale dynamic system. However, few papers have reported on the fast–slow dynamical analysis of a typical complex engineering system coupled hydraulic-mechanical-electric-structure.
In this paper, some interesting physical phenomena of the non-autonomous HTGS with two time scales are investigated. First, the stabilities and dynamic behaviors of the above system are investigated in detail by numerical simulation, which is carried out by using the Runge–Kutta method. Meanwhile, the bifurcation diagram of a traditional model of the HTGS is presented to further study the bifurcation characteristics for the system with two time scales. Third, three typical points are respectively selected based on the bifurcation diagram. Then, the physical phenomena of the bursting oscillations existing in the system with two time scales are described in detail with the combination of the time waveforms and the phase portraits. From an experimental point of view, the spiking state and the quiescent state alternate periodically as the time goes by. Also, stability and operational characteristics vary with system parameter kd. Finally, the comparative analyses for the effect of the bursting oscillations on the system with different amplitudes of the periodic excitation a are carried out. We obtain that the relative deviation of the mechanical torque mt rises with the increase of a.
The future work will involve the investigation into the bifurcation characteristics in theory of the non-autonomous HTGS with two time scales. In addition, the numerical experiments will focus far more on the behavior characteristics of the HTGS with two time scales in the transient process.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |