In recent decades, a large number of devices have been fabricated to satisfy the practical applications for the rapid development of terahertz (THz) technology. Among these devices, optical band-pass filters (BPFs), which are used to transmit a portion of the spectrum while rejecting all other wavelengths, have attracted considerable attention because of their potential applications in fluorescence microscopy, spectroscopy, or imaging.^[1–3] A number of approaches have been proposed to tailor the desired transmission responses and to realize optical devices with stable characteristics from microwave to the THz-gap region.

Metamaterials have attracted a great deal of attention for their remarkable electric or magnetic properties, which rarely exist in the natural materials. By exciting different modes of artificially designed metamaterials, the metamaterials can improve the capacity of the THz communication systems. Moreover, many optical device-based metamaterials, including perfect metamaterial absorbers,^[4,5] phase modulator,^[6] and BPFs,^[7] have been studied in the THz-gap region. A variety of BPFs based on metamaterials have been broadly studied, focusing on how to realize the ultrabroad bandwidth and high transmission rate.^[8–12] Han et al. reported a THz BPF by combining a metal–dielectric–metal (MDM) sandwich with a periodic slot structure.^[13] Chiang et al. experimentally demonstrated an ultrabroad THz BPF based on a composite metamaterial.^[14] Multilayer structures have been employed to modify the bandwidth and the rate of roll-off.^[15] Unlike the multilayer approach, Chen and Fan theoretically reported a multiband THz BPF based on multiple-resonance excitation of a composite metamaterial.^[16]

Particularly, multiband filters possess the potential to improve the capabilities of THz-based communication systems and the remote sensing applications.^[17,18] However, most of the THz BPFs exhibit single or dual-bandpass and polarization sensitivities, and are restricted within wide incident angles, thereby restricting their applications. At present, few design schemes were implemented to construct THz BPFs with multiband transmission responses. In this paper, a triple-band metamaterial BPF in the THz-wave region is proposed, and the transmission spectrum is studied theoretically. To further explain the physical mechanism for the transmission response, the multi-reflection interference principle is utilized to calculate the transmission response of the filter. Given the good performance, the proposed THz BPF by using metamaterials can be a desired candidate in THz applications including imaging and communications.

The proposed triple-band THz BPF is comprised of MDM structure. A dielectric layer with thickness d is sandwiched by two patterned metallic layers with thickness t as shown in Fig. 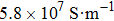1. With a fourfold rotational symmetry along the z axis, the unit cell of the proposed BPF consists of three components, that is, the three nested metallic loops, the dielectric layer, and the cross-shaped metallic line. Both of the metallic layers are 200-nm copper films and have a conductivity of . The polyimide is utilized as a dielectric layer with permittivity and loss tangent of ε = 2.9 and tan δ = 0.02, respectively. All parameters are indicated in Fig. 1, where the dimensions of three loops are orderly denoted as l_i, w_i (i = 1, 2, 3), and the length and width of the cross-shaped line are l₄ and w₄ for a unit cell with period p, respectively.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Schematic structures of the proposed triple-band BPF using metamaterials. (a) Top view of a unit cell and (b) three-dimensional view of the unit cell.

The computer simulation and optimization of the designed BPF were initially carried out by the software CST Microwave Studio^TM based on the finite integration method. To calculate the transmission response, the boundary conditions of the perfectly electric conductor and perfectly magnetic conductor along x and y axes, and the incident electromagnetic (EM) wave propagated along z axis were set. Given that the structure has a fourfold rotational symmetry, the designed BPF was of polarization insensitive to the normal incident EM wave. To explore the filtering performance of the proposed BPF, the focus was on the transmission coefficient S₂₁ and reflection coefficient S₁₁ for normal incident wave. By optimizing the geometrical parameters of the unit cell, such as the lengths and widths of the three loops, the thickness of the dielectric, etc., the S₂₁ and S₁₁ curves were obtained as shown in Fig. 2. The blue solid and red dash lines correspond to S₂₁ and S₁₁, respectively. Full-wave simulations show that the optimized three transmission peaks at central frequencies 0.42, 1.27, and 1.86 THz with corresponding 3-dB band widths of 0.16 THz, 0.11 THz, and 0.10 THz, respectively. Unlike the multilayer approach, the broadband characteristic of our design comes from the hybridization of multiple resonances.^[17] Obviously, the designed filters show narrow bandwidths at resonance frequencies. The structural parameters of the filter unit cell influence the transmission profile naturally. Resonance frequency is inversely proportional to the length of loop.^[19,20] The larger the loop length, the smaller the resonance frequency is. Our previous study also showed that the passband width is mainly determined by the width of loop and it can be widened by increasing the width of loop.^[17] In addition, the permittivity of the dielectric spacer can also affect transmission frequency and bandwidth of the MDM structure remarkably.^[13] The above results suggest that the electromagnetic properties of the integrated MDM structure are dominated by the individual component structures. Therefore, the desired center frequency and bandwidth of bandpass filter can be obtained by selecting appropriate parameters of the MDM structure.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Simulated transmission (blue solid line) and reflection (red dash line) spectra of the triple-band BPF using metamaterials.

To analyze the filtering mechanism of the proposed triple-band BPF, the surface current distributions of the three transmission peaks at 0.42, 1.27, and 1.86 THz are monitored, which are shown in Fig. 3. The arrows indicate the propagation directions of currents on the top and bottom metal layers. As shown in Fig. 3(b), the current distribution at 1.27 THz between the outer loop and middle loop oscillates in the counter direction towards each other. The induced surface currents interfere with each other destructively, giving rise to the so-called “trapped mode” resonance, which stems from the structural symmetry breaking.^[21,22] In addition, the far-field radiations of the current configuration interfere destructively, resulting in dramatic transmission enhancement and reflection reduction. Similarly, the current distribution at 1.86 THz also results in the “trapped mode” resonance, which is shown in Fig. 3(c). For the current distribution at 0.42 THz as shown in Fig. 3(a), the asymmetric current configuration between the top layer and the bottom layer results in another “trapped mode”. Consequently, the excitation of trapped modes is evidenced by the surface current distribution, which contributes to the origin of the strong transmission resonance.^[20] For a trapped mode, the radiation loss is much smaller than the stored field energy, resulting in the transmission increasing at the resonance frequency.^[16]

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) Surface current distributions at frequencies of (a) 0.42 THz, (b) 1.27 THz, and (c) 1.86 THz. The arrows indicate the propagation directions of currents on the top and bottom metal layers.

Besides the numerical simulation of transmission response, an analytical model may be of more help to quantitatively elucidate the filtering mechanism. As is well known, multi-reflection interference theory has been widely used to quantitatively study the transmission spectra of metamaterial absorbers and filters.^{[16,17,23–26]} Here a decoupled system and an interference model were used to calculate the transmission coefficient S₂₁. Figure 4(a) shows the multiple reflection and transmission processes. The used model contains the top and bottom metasurface layers. Here the metasurface layer acted as a partial reflection surface (PRS), which can reflect or transmit part of an incident EM wave. It was assumed that the plane wave was incident in the model at angle α_i. The and were used to denote the top and bottom PRS. At the air (region 1)/ interface, the incident wave is divided into two parts: one is reflected by the PRS to the air with reflection coefficient , and the other is transmitted into the dielectric layer with transmission coefficient . Then, some portion of the transmitted wave is reflected by the interface with reflection coefficient at angle α_s, and the rest is transmitted into air (region 3) with transmission coefficient . Similarly, the total reflection and total transmission are the superpositions of multiple reflections and multiple transmissions at corresponding air (region 1)/ and /air (region 3) interfaces, respectively.^[25,26] The total transmission coefficient is

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. (color online) (a) Physical model used to calculate the complex reflection and transmission coefficients at two interfaces. (b) Magnitudes and (c) phases of the reflection and transmission coefficients for the decoupled model, obtained by the numerical simulation. The coefficients of r21 and t12 (ϕ21, are the magnitudes (phases) of reflection and transmission when the incident wave reaches the air (region 1)//dielectric interface. The coefficients of r23 and t23 (ϕ23, are the magnitudes (phases) of reflection and transmission when the incident wave reaches the dielectric//air (region 3) interface. The β is the phase delay caused by the round propagation in the dielectric spacer. (d) Comparison between the full-wave simulation (black dash line) and theoretical calculation (red solid line) transmission coefficient S21 of the proposed triple-band BPF.

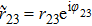
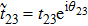
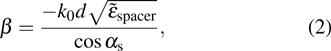The reflection and transmission coefficients at the air (region 1)/ interface or /air (region 3) interface can be derived from numerical simulations of the isolated top metamaterial layer, where the metal is assumed to have effectively zero thickness.^[27,28] Based on the decoupled system and interference model, the magnitude and phase distributions of reflected and transmitted waves at two interfaces are simulated and shown in Figs. 4(b) and 4(c). The calculated transmission coefficient S₂₁ at normal incidence is shown in Fig. 4(d) (red solid line). Three transmission peaks at frequencies of 0.43, 1.27, and 1.85 THz are found to have transmission rates of −0.91, −1.51, and −1.07 dB, respectively, which are in good agreement with the simulated results (black dash line). The calculated results reproduced the simulated results well, and this agreement demonstrates the rationality of utilizing the decoupled system and the interference model to gain a physical insight into the transmission mechanism.^[12,26]

For practical applications, an efficient BPF must not only let the EM wave within certain bands pass through but also maintain the stable wide-angle responses to both TE and TM polarizations. Next, the transmission responses of the designed BPF at various incident angles of the two polarizations were simulated. Figure 5 show the plots of transmission coefficient S₂₁ versus frequency and incident angle for TE and TM polarizations, respectively. The BPF can still maintain stable performances at the three resonance frequencies for both TE and TM polarizations even when the incident angle reaches 30°. Particularly, as the incident angle increases, one or more additional resonances appear in the transmission spectrum in the TM polarization, which are caused by the high order resonant mode in the BPF.^[26]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) Plots of simulated transmission coefficient S21 frequency for different incident angles for (a) TE and (b) TM polarizations.

In this work, a novel THz multiband BPF based on metamaterials is proposed. A multi-reflection interference principle is used to quantitatively analyze the transmission performance of the designed filter. Both the theoretical and simulated results demonstrate that the proposed BPF has three transmission peaks near the frequencies of 0.42, 1.27, and 1.86 THz respectively. Given the symmetry of the structure, the BPF can work with stable performance at wide-angle incident wave for both TE and TM polarizations. The proposed THz BPF shows the merits of a multiband, polarization insensitivity, and wide-angle response. Thus, it can be utilized in a variety of practical applications including spectroscopic detection, phase imaging and THz communication.