Cite this Article
Zhong Han-Hua, Zhou Jian-Hong, Gu Chen-Jie, Wang Mian, Fang Yun-Tuan, Xu Tian, Zhou Jun. Characteristics and mechanism analysis of Fano resonances in Π -shaped gold nano-trimer. Chinese Physics B, 2017, 26(12): 127301  
Permissions
Characteristics and mechanism analysis of Fano resonances in Π -shaped gold nano-trimer
Zhong Han-Hua1, Zhou Jian-Hong2, Gu Chen-Jie1, Wang Mian1, Fang Yun-Tuan3, Xu Tian4, Zhou Jun1, †
Institute of Photonics, Faculty of Science, Ningbo University, Ningbo 315211, China
School of Photoelectric Engineering, Changchun University of Scienceand Technology, Changchun 130022, China
School of Computer Science and Telecommunication Engineering, Jiangsu University, Zhenjiang 212013, China
School of Sciences, Nantong University, Nantong 226007, China

 

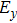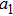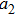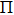
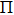
† Corresponding author. E-mail: zhoujun@nbu.edu.cn

Abstract

Fano interference of metallic nanostructure is an effective way to reduce the irradiation loss and improve the spectral resolution. A Π-shaped gold nano-trimer, which is composed of a gold nanorod and two gold nanorices, is presented to investigate the properties of Fano resonances in the visible spectrum by using the finite element method (FEM). The theoretical analysis demonstrates that the Fano resonance of the Π-shaped gold nano-trimer is attributed to the near-field interaction between the bright mode of the nanorice pair and the dark quadrupole mode of the nanorod. Furthermore, by breaking the geometric symmetry of the nanostructure the line-shape spectrum with double Fano resonances of Π-shaped gold nano-trimer is obtained and exhibits structure-dependent and medium-dependent characteristics. It is a helpful strategy to design a plasmonic nanostructure for implementing multiple Fano resonances in practical applications.

PACS: 73.20.Mf;73.22.Lp;81.07.-b
Keyword:Fano resonance;plasmon hybridization;finite element method
1. Introduction

As is well known, Fano resonance is due to the interaction between a continuum of states (background scattering process) and a discrete state (resonant scattering process) producing an asymmetric line-shape spectrum,[1] which can be found in many physics and engineering fields.[2–4] Especially, Fano resonance in metallic nanostructures has attracted more attention due to its numerous benefits for designing photonic devices, such as greatly enhancing the electromagnetic fields localized on the surface of metallic nanostructures,[5] effectively reducing the radiation damping of metal geometry,[6] and vastly inducing the nonlinear effect of materials containing metal nanoparticles.[7] In recent decades, a variety of metallic nanostructures have been proposed to investigate Fano resonances, such as core-shell nanostructures,[8–10] ring-disk cavities,[11–18] nanoparticle dimers,[19–21] nanoparticle trimers,[22,23] and the multimeric nanoclusters.[24–26] Metallic nanostructures have exhibited significant potential applications in photonic devices, such as SERS-based optical sensors,[17,23] spaserbased laser,[27] optical switchers,[28] slow light devices,[29] and resonators with an electromagnetically inducing transparency(EIT)like property.[13,30] Novel metallic nanostructures are expected to be designed and fabricated to demonstrate the excellent functional characteristics of Fano resonance.

In general, a complex noble metal nanostructure can exhibit unique and colorful localized surface plasmon resonance(LSPR) properties under the irradiation of an incident lightwave.[31] According to the plasmon hybridization theory,[32] the extinction spectrum of the noble metal nanostructure can be destructed into the overlap of two or more LSPR bands through the near-field interactions. Further, when the plasmon hybridization between a board bright plasmon mode and a relatively narrow dark plasmon mode happens, a board LSPR band and a relative narrow LSPR band overlap an extinction spectrum with an asymmetric line shape that can be obtained to display the characteristics of Fano resonance, which is dependent on the morphology configurations of the metallic nanostructure.

In terms of the fabrication technique, although some nanostructures composed of nanoparticles can be easily synthesized by the chemical method, the gap distances between nanoparticles and the sizes of nanoparticles are very difficult to control the Focusing ion beam (FIB) method[33] or the electron beam lithography (EBL) method[34] can be used to fabricate more complex nanostructures by controlling the desired pattern, such as the ring-disk nanostructure[12] and nanoclusters,[35] which provides more possibilities and conveniences to study a variety of complex nanostructures theoretically and experimentally. In recent years more delicate metal nanostructures, such as multimer have been proposed to obtain multiple Fano resonances.[36] Compared with single Fano resonance, multiple Fano resonances have several resonant dips which can easily achieve the controllable spectra by adjusting the structure configuration, and the electromagnetic field can be tremendously enhanced at different wavelengths. As a practice example, with the help of the multiple Fano resonances, the Raman spectra of molecules adsorbed on the surface of plasmonic nanostructure can be enhanced efficiently to detect different molecules by matching the different molecules.[37,38]

In our research, a gold nanoparticle system with a Π-shaped trimer composed of a nanorod and two nanorice is proposed to demonstrate the LSPR spectra with Fano resonances. For the symmetric Π-shaped trimer, the extinction spectrum exhibits a single Fano line shape, which originates from the near field coupling between the “bright” dipole mode of the double nanorices and the “dark” quadrupole mode of the nanorod. When the symmetry of the trimer is broken by adjusting the geometry parameters of the nanostructure, double Fano resonances can be formed due to the multiform plasmonic couplings between the modes supported by the asymmetric Π-shaped nanoparticles. The dependence of the double Fano resonance line shape on the refractive index of the surrounding medium is also investigated.

2. Model and calculation method

Figure 1 shows the structure of the Π-shaped trimer. The cylindrical nanorod has length L and radius R. The two nanorices are ellipsoids with polar radii , a2, equatorial radii b1, b2, and , , respectively. The distance between two nanorice is g, and the gaps between the nanorices and the nanorod are d1 and d2. A plane-wave with a polarization in the y direction irradiates on the gold-nanoparticles system along the z direction. Moreover, in all simulations, the experimentally determined dielectric function of gold is used.[39]

Fig. 1. (color online) Schematic diagram of the as-proposed gold nanorod-rice trimer.

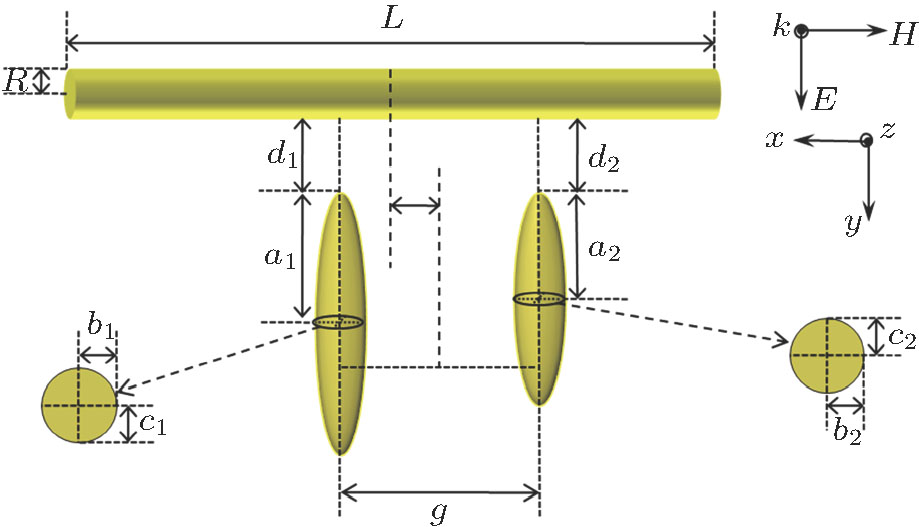
As an effective and high accuracy formulation tool, the finite element method (FEM) is usually used to analyze the optical properties of metallic nanostructures by solving the scattering fields in the frequency domain. Here, we use FEM to calculate the distribution of near-field intensity and the spectra of extinction cross sections of the gold-nanoparticles system shown in Fig. 1. All the numerical simulations are carried out by solving the time-harmonic three-dimensional Maxwell’s equations with the aid of the commercial FEM software package incorporating a radio frequency module (COMSOL Multiphysics 4.1). Adopting adaptive mesh, the absorption cross section and the scattering cross section of the as-proposed nanorod-rice trimer are calculated respectively by the following formulas:[40] Furthermore, the extinction cross section is the sum of the absorption and scattering cross section, it can be calculated as follows: where ε0 is the permittivity of a vacuum, c is the speed of light in a vacuum, is the incident electric field amplitude, is the time average resistive heating, , in which σ is the conductivity of the metal material, , , and ω respectively represent electric field vector, electric displacement vector, and angular frequency of the incident light. is the far-field electric component of the scattering field calculated by the COMSOL implementation of the Stratton–Chu formula.[41]

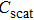
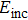
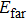
In our simulation, the computation domain includes the rod-rice nano-trimer, a region of free space filled with medium surrounding the nano-system, a far-field transform boundary enclosing the whole system for calculating , and a perfectly matched layer for eliminating the reflections at the domain boundaries. We can obtain by integrating the time average resistive heating of the nano-trimer.

3. Numerical results and analyses
3.1. Fano resonances of the symmetric Π-shaped trimer

As is well known, Fano resonances in the range of the visible spectrum will be significant for the practical applications of biophotonics.[42] For the proposed Π-shaped trimer, the suitable structure parameters are designed to adjust the line shape of Fano resonances to be landed in the range of the visible spectrum. The geometric parameters of the Π-shaped trimer are set to be as follows: L=300 nm, R=20 nm, , , , and g=80 nm, respectively. For the nanorice pair, figure 2(a) shows the dipole LSPR resonant spectrum (red curve) and its corresponding , and the charge distributions at dipole resonant peak 678 nm in the right upper inset, where the incident wave is polarized along the polar radius axis. It displays that the nanorice pair has two identical dipole resonance modes and the red curve in Fig. 2(a) represents their coupling mode. When the incident wave is obliquely irradiated on the nanorod as shown by the black curve in Fig. 2(a), a narrow quadrupole resonance at 692 nm is induced and the corresponding electric field component at the center cut plane and charge distributions are also shown in the right bottom inset.

Fig. 2. (color online) (a) Extinction spectra of the nanorod (black line) and the nanorice pair (red line) under the corresponding excitation conditions (left), and the distributions of electric-fields and charges (right insets, top: nanorice pair, bottom: nanorod); (b) extinction spectrum of the symmetric Π-shaped nano-trimer (left) and the distributions of electric-fields and charges under irradiating wavelengths at the Fano peak and the Fano dip (right insets); (c) normalized extinction spectrum of the symmetric Π-shaped nano-trimer (black line) and the fitted extinction spectrum of the Fano interference model (red dot line).

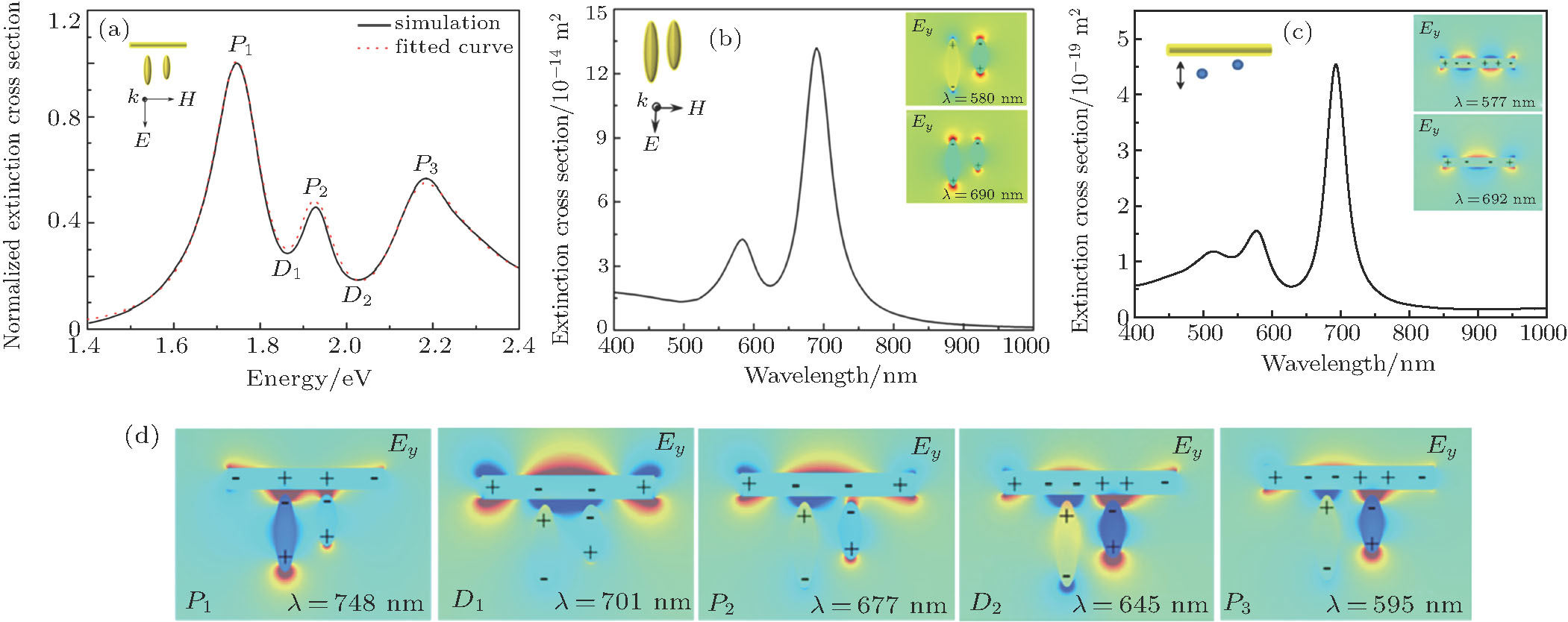
For the Π-shaped trimer, the nanorice pair induces a broad coupling mode (“bright” mode) and excites the narrow quadrupole resonance peak (“dark” mode) of the nanorod by near-field coupling. The excitation process of the trimer mode can be visually expressed as two pathways: direct and indirect excitations, i.e., and , where represents the continuum incident light, denotes the “bright” mode, and the “dark” mode.[43] According to the hybridization theory[32] the overlap between the “bright” mode of the nanorice pair and the “dark” mode of the nanorod creates the strong Fano resonance as shown in Fig. 2(b), where the low energy peak is located at 749 nm, the high energy peak at 653 nm, and a Fano dip D at 694 nm. The and the charge distributions at , D, and are shown in the right upper inset, mid inset, and bottom inset of Fig. 2(b) respectively. It is obviously shown that the dark quadrupole mode of the nanorod is excited by the bright dipole mode of the nanorice pair. We regard as the bonding dipole–quadrupole (BDQ) mode, and as the antibonding dipole-quadrupole (ADQ) mode. Furthermore, from the insets of the charge distributions in Fig. 2(b), we can infer that for the BDQ mode, the quadrupole mode of the nanorod drives the dipolar charge oscillation in the nanorice pair in phase, thereby reducing the resonant energy compared with the dipole mode of only the nanorice pair. On the contrary, for the ADQ mode, the quadrupole mode of the nanorod drives the dipolar charge oscillation in the nanorice pair out of phase, thereby increasing the resonant energy. At the Fano dip, the dipole mode of the nanorice pair is almost canceled by the quadrupole mode of the nanorod, which means that the two pathways to exciting the “bright” mode have the phase difference, which leads to a destructive interference and a deep resonance dip is formed in the extinction spectrum.

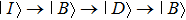
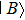
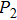
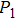
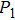
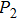
In order to quantify the line widths of the BDQ and ADQ resonances an analytical Fano interference model is used to fit the extinction spectrum[44] and where ar is the constant background amplitude, and bj, , ϕj, ωj are the amplitude, radiative damping, phase, and resonant energy of the j different oscillators. The nonradiative damping γj is negligible for the particles with size approaching the incident wavelength λ due to absorption in the metal. For the trimer structure, converting the abscissa from wavelength into energy and normalizing the extinction cross section, the normalized extinction spectrum (black curve) and the theoretical fitting (red dot line) are shown in Fig. 2(c), where two oscillators (j=1, 2) are used with the fitting parameters: , , , , , , , , . From Fig. 2(c), the fitted curve is well consistent with the normalized extinction spectrum and the extinction spectrum can be construed by the Fano interference model to construct a strong Fano resonance line shape.

3.2. Double Fano Resonances of the asymmetry Π-shaped Nanostructure

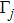
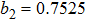
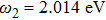
In order to further study the optical properties of the proposed Π-shaped nanostructure, we change the polar radius of one nanorice from 75 nm to 50 nm to obtain an asymmetric Π-shaped trimer nanostructure by breaking the symmetry of the nanorice pair. Figure 3(a) shows the normalized extinction spectrum of the asymmetric Π-shaped trimer in the unit of energy, where the black curve presents the results obtained by FEM and the red dot curve represents the data fitted by the analytical Fano interference model with parameters , , , , , , , , , , , , and . The extinction spectra clearly show double Fano resonances.

Fig. 3. (color online) (a) Normalized extinction spectra (black line) of the Π-shaped nano-trimer and the Fano interference model fitted (red dot line), (b) extinction spectra and the and charge distributions of two nanorice, (c) extinction spectra and the and charge distributions of the nanorod, which is excited by point dipoles (marked with blue point in the inset), and (d) and charge distributions of the Π-shaped nano-trimer at Fano peaks and dips.

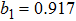
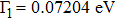
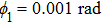
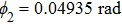
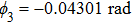
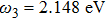
For a better insight into the formation of the double Fano resonances, the interaction between the “bright” mode and “dark” mode originating from asymmetry Π-shaped trimer nanostructure is explored. Figure 3(b) shows the extinction spectrum with a Fano resonance line-shape of the asymmetric nanorice pair, obtained by excitation of a plane wave polarized along the polar radius axis. From the charge distribution patterns in the right insets in Fig. 3(b), the two plasmonic peaks located at 580 nm and 690 nm are attributed to the antibonding mode and the bonding mode, respectively. In Fig. 3(c), the extinction spectrum of the nanorod has a quadrupole mode located at 692 nm and a hexapole mode located at 577 nm, and the right insets show the and the charge distributions of the quadrupole mode and the hexapole mode of the nanorod. The extinction spectrum of the nanorod is obtained by the near-field exciting of plasmonic modes of the nanorice pair. In the simulation, to imitate the responses of the nanorod to the antibonding mode and the bonding mode of the nanorice pair, two electric point dipoles are placed at the center of each nanorice with the same polarization of the incident light. The double Fano resonances of the asymmetric Π-shaped trimer are produced by the interferences between the “dark” mode and the “bright” mode of the nanorice pair and the high “dark” mode of the nanorod.

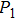
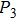
Moreover, Figure 3(d) gives the and the charge distributions corresponding to three peaks and two dips of the double Fano resonances. The plasmon mode corresponding to Fano peak at 748 nm is the coupling mode between the bonding mode of the nanorice pair and the quadrupole mode of the nanorod (BCQ mode), and the plasmon mode corresponding to at 677 nm origins from the antibonding mode of the nanorice pair coupled with the quadrupole mode of the nanorod (ACQ), and the plasmon mode corresponding to at 595 nm is caused by coupling beween the antibonding mode of the nanorice pair and the hexapole mode of the nanorod (ACH).

For the BCQ peak, the quadrupole mode of the nanorod drives the dipolar charge oscillation in the bonding mode of the nanorice pair in phase, thereby reducing the restoring force and lowering the resonant energy compared with those of the single bonding mode of the nanorice pair and the quadrupole mode of the nanorod. That is why the resonant wavelength of the BCQ peak is greater than those of the bonding mode of the nanorice pair and the quadrupole mode of the nanorod; it is the same reason why the resonant wavelength of the ACH peak is greater than those of the antibonding mode of the nanorice pair and the hexapole mode of the nanorod. For the ACQ peak, the interaction between the antibonding mode of the nanorice pair and the quadrupole mode of the nanorod is weak, and there is a relatively small shift of the ACQ peak with respect to the quadrupole peak of the nanorod.

3.3. Structure-dependent characteristics of the double Fano resonance

In order to investigate the dependence of the double Fano resonances on the geometry parameters of the asymmetric Π-shaped trimer, by adjusting the sizes of nanoparticles, the extinction spectra of asymmetric structure are obtained and shown in Fig. 4. All the BCQ, ACQ and ACH modes are red shifted with the increasing of L or a1. When increasing L from 290 nm to 330 nm, the intensity of the BCQ mode decreases, while the intensity of the ACQ peak increases as shown in Fig. 4(a).

Fig. 4. (color online) (a) Extinction spectra of the asymmetric Π-shape trimer with different lengths of nanorod L, (b) extinction spectra of the Π-shape trimer with different polar radii of two nanorice and at a fixed ratio of .

Both ACQ mode and BCH mode increase their intensities with the increasing of polar radii of two nanorice as shown in Fig. 4(b). The effect mainly lies in the interaction between the “bright” mode of the nanorice pair and the higher “dark” mode of the nanorod. The changes of the geometry parameters of the asymmetric Π-shaped trimer shift the resonance frequencies of the plasmonic modes supported by the nanorice pair and the nanorod, which results in the changes of the double Fano lineshaped extinction spectrum.

On the other hand, the double Fano resonances are also dependent on the distances among the nanoparticles. Figure 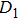5(a) displays the extinction spectra of the asymmetric Π-shaped trimer versus the gap size d between the nanorice pair and the nanorod. With the increasing of the gap size d ACQ mode red-shifts and BCQ mode blue-shifts, and they approach to the bonding mode of the nanorice pair and the quadrupole mode of the nanorod, respectively. At the same time, the BCH mode is gradually close to the antibonding mode of the nanorice pair. The Fano dip turns shallower because the “bright” mode of the nanorice pair is weakly coupled to the higher “dark” mode of the nanorod by reducing the coupling strength.

Fig. 5. (color online) (a) Extinction spectra for different values of coupling gap size d between the nanorice and the nanorod, and (b) extinction spectra for different distances between two nanorice g, the right upper inset shows the at the resonance peak with g=180 nm, and the right bottom inset displays the at the resonance peak with g=300 nm.

The distance between two nanorice grains also affects the double Fano resonances of the asymmetric Π-shaped trimer. As shown in Fig. 5(b) as g increases from 80 nm to 180 nm, the ACQ mode is red-shifted and the BCQ mode is blue-shifted, and also the Fano dip becomes shallow. It could be attributed to the mechanism of Fano resonance based on the near-field distributions of the “bright” mode and the “dark” mode. The coupling between the higher “dark” mode of the nanorod and the “bright” mode of the nanorice pair becomes weak when their near-field overlapping decreases with the increasing of g as shown in the right upper inset of Fig. 5(b). However, when the distance between two nanorice grains increases from 180 nm to 300 nm, the BCQ and ACQ modes move oppositely and bring out the Fano resonance again due to the “bright” mode of the nanorice pair effectively interacting with the “dark” mode of the nanorod as shown in the right bottom inset of Fig. 5(b). The shifts of the BCH modes are small for the change of g because this effect is determined by the narrow hexapole mode of the nanorod, and the change of the separation between two nanorice grains has less influence on the near-field coupling between the hexapole mode of the nanorod and the antibonding mode of the nanorice pair.

3.4. Medium-dependent characteristics of the double Fano resonance

In general, the Fano resonance of the metal nanostructure is intensely sensitive to the surrounding medium because the plasmonic resonance of the metal nanostructure depends on the permittivity of the surrounding medium. The extinction spectra of the proposed asymmetric Π-shaped trimer surrounded by media with different refractive indices are shown in Fig. 6(a). When the refractive indices of the surrounding media increase from 1.1 to 1.5, all three plasmon modes (ACH, ACQ, and BCQ modes) and two Fano resonant dips ( and ) are red-shifted. We normally use the resonance wavelength shift per refractive index unit (RIU) to define the sensitivity of the nanosystem[45]. Figure 6(b) shows that the wavelengths corresponding to the plasmon modes and Fano dips linearly increase with the increasing of the refractive index of the surrounding medium with different slopes of wavelength changes per refractive index unit. Additionally, the figure of merit (FOM) is usually used to evaluate the overall performance of the metal nanostructure as a refractive index sensor, which can be defined as[46] where the FWHM stands for full width at half maximum at the wavelength λ corresponding to the plasmon mode of metal nanostructure, and can be obtained from the Fano interference model which is the refractive index sensitivity.[44] For the asymmetric Π-shaped trimer, FOMs of the ACH mode, the ACQ mode and the BCQ mode are approximately 9.1, 19.0, and 13.2, respectively, which are higher than the experimental values in Ref. [47]. The proposed asymmetric Π-shaped trimer nanostructure has attractive applications for designing the refractive index sensor due to its high refractive index sensitivity and good FOM.

Fig. 6. (color online) (a) Extinction spectra of the asymmetric Π-shaped trimer surrounded by media with different refractive indices, (b) resonance wavelengths of the ACH, the ACQ, the BCQ modes, Fano dip and with different surrounding refractive indices, and the refractive index sensitivities of plasmon modes and Fano dips are calculated and shown in the left upper corner.
4. Conclusions

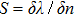
In this work a Π-shaped nano-trimer is proposed to produce strong Fano resonance. The single Fano resonances of the symmetric Π-shaped trimer and the double Fano resonance of the asymmetric Π-shaped trimer are respectively investigated by analyzing the interferences among the dark quadrupole mode of the nanorod, the bright dipole plasmonic modes of the nanorice pair, and higher “dark” modes of the nanorod generated from the different hybridized modes of the nanorice pair. The simulation results demonstrate the structure-dependent and the medium-dependent characteristics of the double Fano resonance. Following this design idea, multiple Fano resonances are obtained for the multiple wavelength active plasmonic switching, SERS, and bio-sensing applications.

Reference
[1] Fano U 1961 Phys. Rev. 124 1866
[2] Kobayashi K Aikawa H Sano A Katsumoto S Iye Y 2004 Phys. Rev. 70 035319
[3] Zhang W W Feng Y M Zhang Y X Chen W L Lin W 2015 J. Phys. D: Appl. Phys. 48 275102
[4] Miroshnichenko A E Kivshar Y S 2005 Phys. Rev. 72 056611
[5] Ye J Wen F Sobhani H Lassiter J B Dorpe P V Nordlander P Halas N J 2012 Nano Lett. 12 1660
[6] Huo Y Y Jia T Q Zhang Y Zhao H Zhang S A Feng D H Sun Z R 2013 Sensors 13 11350
[7] Romani E C Vitoreti D Gouvêa P M Caldas P G Prioli R Paciornik S Fokine M Braga M B Gomes S L Carvalho I C 2012 Opt. Express 20 5429
[8] Pe na-Rodríguez O Rivera A Campoy-Quiles M Pal U 2013 Nanoscale 5 209
[9] Chen J Shen Q Chen Z Wang Q G Tang C J Wang Z L 2012 J. Chem. Phys. 136 214703
[10] Wang B B Zhou J Zhang H P Chen J P 2014 Chin. Phys. 23 87303
[11] Liu S D Yang Z Liu R P Li X Y 2011 J. Phys. Chem. 115 24469
[12] Chen L Y Tang Z X Gao J L Li D Y Lei C X Cheng Z Z Tang S L Du Y W 2016 Chin. Phys. 25 113301
[13] Hao F Nordlander P Sonnefraud Y Dorpe P V Maier S A 2009 ACS Nano 3 643
[14] Sonnefraud Y Verellen N Sobhani H Vandenbosch G A Moshchalkov V V Dorpe P V Nordlander P Maier S A 2010 ACS Nano 4 1664
[15] Zhang Y Jia T Q Zhang H M Xu Z Z 2012 Opt. Lett. 37 4919
[16] Cetin A E Altug H 2012 ACS Nano 6 9989
[17] Fu Y H Zhang J B Yu Y F Luk’yanchuk B 2012 ACS Nano 6 5130
[18] Li J Liu T Zheng H Dong J He E Gao W Han Q Wang C Wu Y 2014 Plasmonics 9 1439
[19] Ci X T Wu B T Song M Liu Y Chen G X Wu E Zeng H P 2014 Appl. Phys. 117 955
[20] Huang M Chen D Zhang L Zhou J 2016 Chin. Phys. 25 057303
[21] Wu D J Jiang S M Liu X J 2012 J. Phys. Chem. 116 13745
[22] Metzger B Schumacher T Hentschel M Lippitz M Giessen H 2014 ACS Photon. 1 471
[23] He J N Fan C Z Ding P Zhu S M Liang E J 2016 Sci. Rep. 6 20777
[24] Shafiei F Monticone F Le K Q Liu X X Hartsfield T Alù A Li X 2013 Nat. Nanotechnol. 8 95
[25] Lassiter J B Sobhani H Knight M W Mielczarek W S Nordlander P Halas N J 2012 Nano Lett. 12 1058
[26] Rahmani M Lukiyanchuk B Ng B KG A T Liew Y F Hong M H 2011 Opt. Express 19 4949
[27] Zheng C J Jia T Q Zhao H Zhang S A Feng D H Sun Z R 2015 Appl. Phys. 49 015101
[28] Li J B He M D Wang X J Peng X F Chen L Q 2014 Chin. Phys. 23 067302
[29] Papasimakis N Zheludev N I 2009 Opt. Photon. News 20 22
[30] Zhang J Xiao S Jeppesen C Kristensen A Mortensen N A 2010 Opt. Express 18 17187
[31] Barnes W L Dereux A Ebbesen T W 2003 Nature 424 824
[32] Nordlander P Oubre C Prodan E Li K Stockman M I 2004 Nano Lett. 4 899
[33] Freeman D Madden S Luther-Davies B 2004 Optoelectronic and Microelectronic Materials and Devices 157 160 157–60
[34] Hao F Sonnefraud Y Dorpe P V Maier S A Halas N J Nordlander P 2008 Nano Lett. 8 3983
[35] Hentschel M Saliba M Vogelgesang R Giessen H Alivisatos A P Liu N 2010 Nano Lett. 10 2721
[36] Yang D J Yang Z J Li Y Y Zhou L Hao Z H Wang Q Q 2015 Plasmonics 10 263
[37] Wang J Fan C He J Ding P Liang E Xue Q 2013 Opt. Express 21 2236
[38] Yin L Y Huang Y H Wang X Ning S T Liu S D 2014 AIP Adv. 4 077113
[39] Johnson P B Christy R W 1972 Phys. Rev. 6 4370
[40] Knight M W Halas N J 2008 New J. Phys. 10 105006
[41] Stratton J A 1941 Electromagnetic Theory New-York McGrow-Hill
[42] Niu L Zhang J B Fu Y H Kulkarni S Lukyanchuk B 2011 Opt. Express 19 22974
[43] Fan J A Bao K Wu C Bao J Bardhan R Halas N J Manoharan V N Shvets G Nordlander P Capasso F 2010 Nano Lett. 10 4680
[44] Verellen N Van Dorpe P Huang C Lodewijks K Vandenbosch G A Lagae L Moshchalkov V V 2011 Nano Lett. 11 391
[45] Sun Y Xia Y 2003 Analyst 6 686
[46] Sherry L J Chang S H Schatz G C Van Duyne R P Wiley B J Xia Y 2005 Nano Lett. 5 2034
[47] Chong K E Orton H W Staude I Decker M Miroshnichenko A E Brener I Kivshar Y S Neshev D N 2017 Phil. Trans. R. Soc. 375 20160070