Cite this Article
Konovalov Sergey, Zagulyaev Dmitry, Chen Xi-Zhang, Gromov Victor, Ivanov Yurii. Variations in defect substructure and fracture surface of commercially pure aluminum under creep in weak magnetic field. Chinese Physics B, 2017, 26(12): 126203  
Permissions
Variations in defect substructure and fracture surface of commercially pure aluminum under creep in weak magnetic field
Konovalov Sergey1, 2, Zagulyaev Dmitry3, Chen Xi-Zhang1, 2, †, Gromov Victor3, Ivanov Yurii4
Samara National Research University, Samara 443086, Russia
Wenzhou University, Wenzhou 325035, China
Siberian State Industrial University Novokuznetsk, 654007, Russia
Institute of High Current Electronics of the Siberian Branch of the Russia Academy of Sciences, Tomsk 634055, Russia

 

† Corresponding author. E-mail: chenxizhang@wzu.edu.cn

Project supported by the Ministry of Education and Science of Russian Federation (State Task No. 3.1283.2017/4.6).

Abstract

Commercially pure polycrystalline aluminum of grade A85, as a test material, is investigated. Using scanning and transmission electron microscopy the aluminum fine structure and fracture surface are analyzed. Fractures are studied in the regime of creep with and without a simultaneous effect of 0.3-T magnetic field. It is found that the application of a magnetic field in a linear stage of creep leads to substructure imperfection increasing. Furthermore, the magnetic field effect on aluminum in the process of creep causes the average scalar density of dislocations to increase and induces the process of dislocation loop formation to strengthen. Fractographic investigation of the fracture surface shows that in the fibrous fracture zone the average size of plastic fracture pits decreases more than twice under creep in the condition of external magnetic field compared with in the conventional experimental condition. In a shear zone, the magnetic field causes the average size of fracture pits to decrease. Experimental data obtained in the research allow us to conclude that the magnetic field effect on aluminum in the process of creep leads to the fracture toughness value of the material decreasing, which will affect the state of defect substructure of the volume and surface layer of the material. The influence of the magnetic field is analyzed on the basis of the magneto-plasticity effect.

PACS: 62.20.Hg;61.72.Lk;41.20.-q;68.37.Hk
Keyword:aluminum;magnetic field;creep;structure
1. Introduction

Intensive development of engineering and modern technologies leads to the production of powerful energy devices generating magnetic and electric fields. As the majority of structures and mechanisms working in the condition of mechanical loads (e.g. creep) are subjected to fracture, the study of metal behavior in the conditions of an external energy effect is necessary for analyzing their service lives.[1–7]

In the last decade a lot of investigations were carried out and indicated that even a weak magnetic field (1 T) is able to change substantially the kinetic process, integral strength, and plastic characteristics of the solid body subjected to deformation.[8–12] It is conventional to relate the nature of this phenomenon to the spin conversion in impurity centers, which results in their electron structure transformation and corresponding decrease in their interaction with dislocations.[13,14] It facilitates the dislocation displacement (it plastifies the material) reducing the deformation properties relating to the mean path between obstacles.

Unfortunately, the investigations devoted to establishing the magnetic field effect on the process of plastic deformation of polycrystalline metals are insufficient. For understanding the physical nature of metal fracture under creep conditions in a magnetic field, it is necessary to conduct a complex investigation including the studies of dislocation substructure evolution at different degrees of deformation and relief of fracture surface, which are to be studied in this paper.

2. Material and procedure

Commercially pure polycrystalline aluminum A85 was chosen as a test material. The samples had the shape of plates with a size of 150×5×0.46 mm. Preliminary preparation of the initial structure consisted in recrystallization annealing at 770 K for 2 hours. Then at room temperature the samples were subjected to creep with constant tensile stress δ = 65 MPa up to fracture ( ). The first half (15 samples) were deformed under the conditions of an external magnetic field of 0.3 T, the second half were under the condition of no magnetic field.

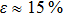
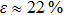
The structures of samples were studied by transmission electron diffraction microscopy, where the foils in transmitted light were prepared from the volume of the material located in the central part of the sample (at ) and from that one adjacent to fracture zone (at ). The fracture surface was studied by scanning electron microscopy using device “SEM 515 Philips”. Parameters of material structure and fracture surface were determined by the method of stereology.[15]

3. Experimental results and discussion
3.1. Studies of material dislocation structure formed under creep

The substructures formed in aluminum under creep (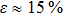 ) are analyzed according to the observations of grain-subgrain (cell-block) microstructures in the presence and absence of the external magnetic field. Average block sizes are independent of the condition of the test and they are D = 1.6 mm for isotropic grain longitudinal size D = 0.65 mm and transverse size L = 1.5 mm for anisotropic grain, and anisotropy coefficient k = L/D = 2.3.

In the volume of cell-blocks, different dislocation substructures are revealed: chaotic, net-like, cellular structure, and dislocation loops as shown in Figs. 1(a)–1(d), respectively.

Fig. 1. Types of dislocation substructures formed in aluminum under creep: chaotic (a); net-like (b); cellular one (c); dislocation loops (d).

Scalar dislocation density and volume fraction of substructure type are used as the parameters characterizing the dislocation substructure. The results of quantitative analysis of dislocation substructure are shown in Figs. 2 and 3.

Fig. 2. Distributions of volume fraction of dislocation substructure types depending on value of deformation without magnetic field (a) and with B = 0.3 T (b).
Fig. 3. (color online) Variations of average scalar dislocation density (a) and dislocation loops (b) with deformation without magnetic field and with B = 0.3 T.

When analyzing the results shown in Figs. 2 and 3, it can be noted that the main type of dislocation structure is a chaotic one, no matter whether a magnetic field exists in the experiment. Its volume fractions are 72% and 77% for and in the absence of a magnetic field, respectively. The more explicit distinctions are observed in the correlation between scalar dislocation density and dislocation loops: creep results in the scalar dislocation density increasing more than 3 times and dislocation loops forming. Here the values of both parameters of the dislocation substructure are higher in aluminum deformed in the presence of a magnetic field. It should be noted that the higher the density of dislocation loops, the more the degree of pinning of dislocations is and the higher the strength of material.

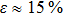
In the volume of the material adjacent to the fracture zone the chaotic, net-like and cellular dislocation structures and dislocation loops are revealed. The main dislocation structure is a chaotic one, which is independent of the magnetic field effect (Fig. 2).

Studies of fracture zone structure (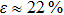 ) show that the magnetic field affects significantly the density of dislocation loops: creep in the presence of an external magnetic field results in the formation of a structure whose density of dislocation loops is twice higher than under creep in conventional conditions (Fig. 3). It is apparent that these loops are formed as a result of agglomeration in disks of point defects—vacancies and interstitial atoms generated by plastic deformation.

Accordingly, the external magnetic field results in the intensification of the process of vacancies and interstitial atoms formation under creep of aluminum. The dislocation loops and dislocations in the material at their sufficiently high density can increase the material strength.

3.2. Studies of aluminum fracture surface formed under creep

Macroscopic view of the fracture surface of an aluminum flat sample fractured in tension in conditions of creep is shown in Fig. 4. Two zones are revealed, i.e., fibrous zone and shear zone. This fact is indicative of aluminum fracture in the conditions of steady crack growth. The fibrous zone, formed by fracture pits constituting a half of micropore through which fracture occurs, occupies the basic area of the facture surface. The shear zone in the sample fractured in ordinary conditions occupies an insignificant (of the order 10%) part of the fracture surface (Fig. 4(a)) and is more obvious in the sample fractured in the conditions of an external magnetic field (of the order of 30%) (Fig. 4(b)).

Fig. 4. Fractographs of fracture surfaces. Creep in the usual condition (without magnetic field) (a) and with an external magnetic field (b).

Typical fractographs for tested samples demonstrating fracture pits are shown in Fig. 5. Near pits and on their internal surface the wavy thin lines are seen (the lines are pointed out by arrows).

Fig. 5. Fractographs showing fracture pits.

The test shows that pit growth occurs by slipping gliding of the material along many active systems. Consequently, regardless of the creep testing procedure the aluminum fracture surface are plastic ones with high density of slip bands and deep pits are indicative of the high local plasticity of the material.

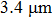
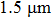
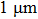
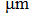
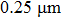
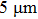
Deformation of aluminum in the condition of creep results in the formation of the fracture surface with a wide range of sizes of plastic fracture pits (Fig. 5). Statistical analysis of the fracture surface, performed in the research, shows that the average size (diameter) of plastic fracture pits depends on both the experimental condition and the positions of their formation (fibrous zone and shear zone). Namely, in the fibrous fracture zone under creep without a magnetic field the average size of plastic fracture pits is ; the creep in the condition of an external magnetic field results in the average size of plastic fracture pits decreasing more than twice ( ). Simultaneously, the existing interval of pit sizes decreases: in experiments without magnetic field the pit size varies from to 9 ; the presence of a magnetic field causes the limiting pit sizes to decrease from to .

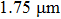
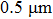
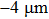
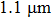
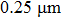
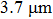
Shear zones in the studied samples also contain plastic fracture pits (shear pits) (Fig. 4). The performed quantitative studies show that in this case the average sizes of plastic fracture pits, independent of experimental conditions, are slightly less than plastic fracture pits formed in fibrous fracture zones. Namely, in tests without a magnetic field the average sizes of plastic fracture pits are (minimal sizes ; maximum ); for the sample fracture in the presence of a magnetic field, the average sizes of plastic fracture pits are (minimal ; maximal ).

The shape and pit depth (micropores) may be related to fracture toughness under the condition of one material testing and an identical scheme of loading. Deep conical pits are often observed in fractures of very ductile materials.[15] It is believed that the increase in crack resistance is accompanied by the increase in pit depth at the fracture surface. If the pit depth of plastic fracture is assumed to be proportional to pit size then it can be concluded that the use of an external magnetic field facilitates some decrease of the fracture toughness of aluminum in the condition of creep.

3.3. Analysis of behavior of metallic material atoms in external magnetic field

Now, we consider the behavior of metallic material atoms in an external magnetic field.

Aluminum is a paramagnetic material, a substance, whose magnetic moment is not equal to zero, possessing paramagnetic properties. The valence electron shell of an aluminum atom consists of three electrons but the shell itself has the form 3s23p. Therefore, it is paramagnetic and the magnetic moment of its atom is not equal to zero. The admixture in aluminum A 85 contains an iron content of 0.22% of mass fraction. Iron, in turn, is ferromagnetic and has eight valence electrons: 4s2 and 3d6.

In the process of plastic deformation, there occur continuous interactions of dislocations with each other and also with point defects that may be para- or ferro-magnetic interstitial and substitutional atoms, which are iron atoms in our case.

If the interaction of dislocation of paramagnetic material with ferromagnetic impurities and other dislocation is assumed to not only have the elastic characteristic but also be accompanied by the formation and breakage of a covalent bond between them, then it may be noted that the interaction of dislocation is an additional factor of dislocation retardation because additional energy is necessary for breaking the covalent bond (Fig. 6).

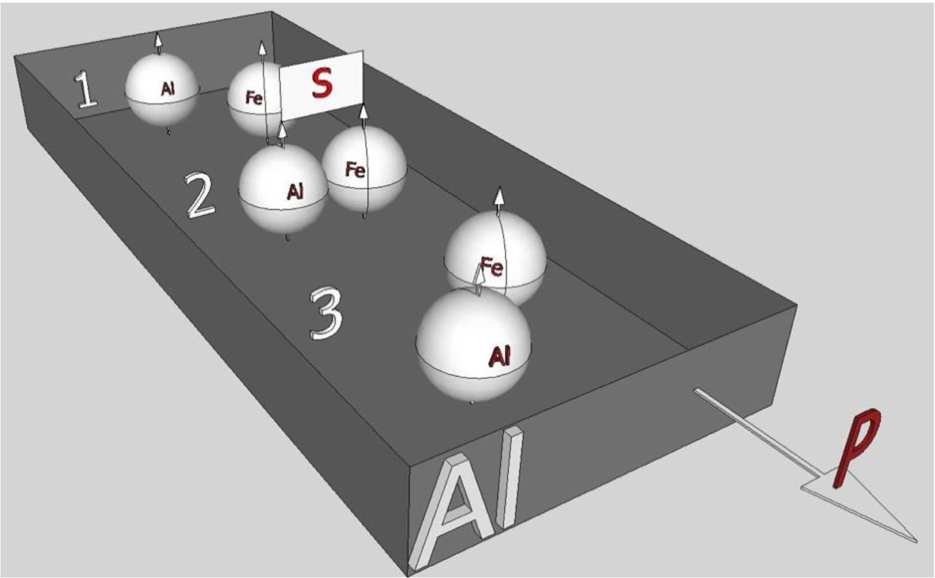Fig. 6. (color online) Interactions of aluminum atoms with iron atoms in the process of plastic deformation without magnetic field.

The formation of a covalent bond between one atom belonging to dislocation and ferromagnetic impurity defect or atom of other dislocation is possible because both aluminum and iron atoms have electrons with unpaired spin.[8,16] Thus, the process of plastic deformation is accompanied by chemical reactions that are repeated many times.

We come to consider the running of the plastic deformation process in time in the absence of a magnetic field. Figure 6 illustrates the different time stages of the process; number 1 indicates that aluminum atom belonging to the dislocation approaches to the point defect presented by paramagnetic or ferromagnetic interstitial and substitutional atoms (see Fig. 6 for the iron atom example). Further, besides the elastic interaction, a covalent bond is formed in the S state between one atom belonging to the dislocation and point defect, which is indicated by number 2. At a later time the movement of the atom belonging to dislocation is related to the elastic overcoming of the obstacles and the breaking of the covalent bond from the S state. At this point the total energy necessary for overcoming the obstacle is combined with the energy necessary for overcoming the electric interaction and the energy necessary for breaking the covalent bond. After the interaction occurs the dislocation continues its further movement to the next obstacle, which is indicated by number 3. Figure 7 shows the plastic deformations in the presence of a magnetic field, time moments 1 and 4 refer to the approaching and removing of the dislocation from the point defect. However, after the formation of covalent bond 2 under the action of the magnetic field, the transition of a radical pair from the S state to the T state and its further breaking take place, in this case the energy necessary for breaking the covalent bond from the T state is less than from the S state.

Fig. 7. (color online) Interactions of aluminum atoms with iron atoms in the process of plastic deformation under the action of magnetic field.

From the above discussion it may be concluded that a magnetic field has an indirect effect on the process of plastic deformation. It may be supposed that the magnetic field, when affecting the covalent bond, transforms a radical pair from the singlet state to a triplet one, which makes its breakage easier because the energy necessary for breakage of a radical pair in a singlet stage is larger than in a triplet one (Fig. 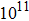7).[12] It results in the increase of dislocation mobility and since 106– dislocations per 1 cm2 are usually present in a crystal, their displacements lead to macroscopic deformations. The changes in mobility of these defects are immediately reflected on macroscopic parameters of the system, in particular, which results in the changes of the mechanical properties of crystals and supports the research results in Refs. [17]–[19], where it is shown that with the increase in dislocation mobility the micro-hardness of bismuth crystals decreases.

4. Conclusions

The studies of commercially pure aluminum show that in the presence of a magnetic field a larger accumulation of scalar density of dislocations takes place. It allows us to study the microstructure of dislocation chaos and the developing process of dislocation loop formation. Investigations of the fracture zone show that in the presence of a magnetic field the intensification of the dislocation loop formation process happens, assisting in material strength increase. By scanning electron microscopy it is observed that in the presence of a magnetic field the fracture surface (with pits of plastic fracture) formed has a smaller average size than in the ordinary conditions of the experiment. From these results it can be concluded that the magnetic field leads to some decrease in fracture toughness of commercially pure aluminum under the deformation in creep condition, which can affect the state of defect substructure volume and the surface layer of the material. A magnetic field has an indirect effect on the process of plastic deformation. It may be supposed that a magnetic field, when affecting the covalent bond, transforms a radical pair from the singlet state to the triplet one, and thus makes its breakage easier because the energy necessary for breaking the radical pair in a singlet stage is larger than in a triplet one.

Reference
[1] Sahin O Ucar N 2006 Chin. Phys. Lett. 23 3037
[2] Wang H M Zhu Y Li G R Zheng R 2016 Acta Phys. Sin. 65 146101 (in Chinese)
[3] Zuo X W An B L Huang D Y Zhang L Wang E G 2016 Acta Phys. Sin. 65 137401 (in Chinese)
[4] Li G R Xue F Wang H M Zheng R Zhu Y Chu Q Z Cheng J F 2016 Chin. Phys. 25 106201
[5] Aciksoz E Soylu A Bayrak O 2016 Chin. Phys. 25 100302
[6] Liu Y J Lin Z Q Wang J F 2016 Physics 45 19 (in Chinese)
[7] Peng T Li L 2016 Physics 45 11 (in Chinese)
[8] Golovin Y I 2004 Phys. Solid State 46 789
[9] Konovalov S V Zagulyaev D V Yaropolova N G Komissarova I A Ivanov Y F Gromov V E 2015 Russ. J. Non-Ferrous Met. 56 441
[10] Zagulyaev D V Konovalov S V Yaropolova N G Ivanov Y F Komissarova I A Gromov V E 2015 J. Surf. Investig X-Ray, Synchrotron Neutron Tech. 9 410
[11] Zagulyaev D V Konovalov S V Litvinenko N G Komissarova I A Gromov V E 2013 Tsvetnye Met. 4 74
[12] Alshits V I Darinskaya E V Koldaeva M V Petrzhik E A 2003 Crystallography Reports 48 768
[13] Alshits V I Urusovskaya A A Smirnov A E Bekkauer N N 2000 Phys. Solid State 42 277
[14] Li G R Wang F F Wang H M Zheng R Xue F Cheng J F 2017 Chin. Phys. 26 046201
[15] Jin Z Sun C T 2012 Fracture Mechanics Elsevier Inc.
[16] Golovin Y I 2004 J. Mater Sci. 39 5129
[17] Pinchook A I Shavrei S D 2002 Technical Physics Letters 28 525
[18] Shavrei S D Pinchook A I 2003 Technical Physics Letters 29 632
[19] Pinchuk A I Shavrei S D 2001 Phys. Solid State 43 39