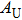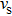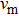† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61601468), the Fundamental Research Funds for the Central Universities, China (Grant No. 3122014C024), and the Fund for Scholars of Civil Aviation University of China (Grant No. 2013QD06X).
The structural, mechanical, elastic anisotropic, and electronic properties of the monoclinic phase of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 are systematically investigated in this work. The calculated results of lattice parameters, elastic constants and elastic moduli of m-Si3N4 and m-Ge3N4 are in good agreement with previous theoretical results. Using the Voigt–Reuss–Hill method, elastic properties such as bulk modulus B and shear modulus G are investigated. The calculated ratio of B/G and Poisson’s ratio v show that only m-SiGe2N4 should belong to a ductile material in nature. In addition, m-SiGe2N4 possesses the largest anisotropic shear modulus, Young’s modulus, Poisson’s ratio, and percentage of elastic anisotropies for bulk modulus 

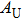
Nitrides consisting of III A and IV A group elements can be used as high temperature materials, catalysts, light-emitting diodes and refractory ceramics because of their excellent mechanical and thermodynamic properties.[1–4] Silicon nitride is an important ceramic material. It is a superhard material and atomic crystal which has good lubricity and abrasion resistance. It resists oxidation at high temperature, and it can resist cold and hot shocks, it can be heated to over 1000 K in the air and will not be broken by rapid cooling and rapid heating. Because silicon nitride ceramic has such excellent characteristics, it is often used in bearings, gas turbine blades, mechanical seals, permanent die, and other mechanical components. If the silicon nitride ceramic with high temperature resistance and high heat transfer resistance is used to make the heating surfaces of the engine parts, it can not only improve the quality of diesel engine, save fuel, but also enhance the thermal efficiency. In fact, germanium is adopted because Ge atoms have higher carrier mobility than Si atoms. The semiconductor field effect transistor has superior performances. The germanium atom radius is bigger, so the critical pressure of the phase transition of Ge3N4 is less than that of Si3N4. Germanium nitride also has the advantages of corrosion resistance, high hardness, and its band gap can be adjusted. Many new structures of silicon nitride and germanium nitride have been reported in many researches.[5–8] It has been known for several decades that silicon nitride exists in two stable phases (namely α- and β-Si3N4) with very similar structures,[5] they both have hexagonal symmetry. The phase boundaries of the 
The structural, electronic, and optical properties of the new cubic spinel nitrides c-Si3N4, c-SiGe2N4, c-Si2GeN4, and c-Ge3N4 were studied by a first-principles method.[9] The c-SiGe2N4 is a direct band gap semiconductor with a band gap of 1.85 eV, and the c-Si2GeN4 is an indirect band gap semiconductor with a band gap of 2.56 eV. In addition, the bulk moduli of c-SiGe2N4 and c-Si2GeN4 are 277.1 GPa and 258.3 GPa, respectively. Using first-principles calculations, the structural, electronic, elastic, and optical properties of cubic spinel SiGe2N4 under pressure were investigated by Moakafi et al.[10] Bouhemadou et al.[11] have investigated the structural, elastic, electronic, optical and thermal properties of c-SiGe2N4 by using the ultrasoft pseudopotential density functional method in the generalized gradient approximation under pressure. The structural and mechanical properties of the cubic spinel c-CSi2N4 were studied by first-principles total energy calculations based on the density-functional theory.[12] The Vickers hardness of c-CSi2N4 is 52.07 GPa, so it is a potential superhard material. Cui et al. explored three Si3N4 metastable phases, i.e., tetragonal t-Si3N4, monoclinic m-Si3N4 and orthorhombic o-Si3N4, by analyzing the crystal structure obtained through using the particle swarm optimization (CALYPSO) code.[13] The m-Si3N4 belongs to the space group of Cm in a monoclinic system and it is mechanically and dynamically stable under ambient pressure based on their elastic constants and phonon dispersions calculations. Cang et al. predicted the lattice structures, densities of states, phonon dispersion curves of m-, t-, and o-Ge3N4.[14] The stabilities of these Ge3N4 structures were verified by the proving of negative formation enthalpy, the satisfying of Born’s stability criteria and no imaginary frequency in the phonon dispersion curves in a pressure range of 0 GPa–20 GPa. Fan et al. investigated the electronic structures, elastic, anisotropic, and electronic properties of m-Si3N4, t-Si3N4, and o-Si3N4 under pressure,[15] and it is interesting that the shift of band gap from direct to indirect occurs for m-Si3N4 when the pressure rises up to 50 GPa. Chen et al.[16] predicted the structural, electronic, optical and thermodynamic properties of m-, t-, and o-M3N4 (M = Si, Ge, Sn).
According to the previous work, we predict two new double nitrides m-Si2GeN4 and m-SiGe2N4 in the Cm space group. In the present work, the structural, elastic anisotropic, and electronic properties of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 are investigated using density functional theory calculations. The Debye temperature, the ductile or brittle characters and elastic anisotropy of m-SixGe3−xN4 (x = 0, 1, 2, 3.) are discussed in detail.
The structural optimizations and property predictions of the monoclinic structures of m-SixGe3−xN4 (x = 0, 1, 2, 3) were performed based on density functional theory (DFT)[17,18] as implemented in the Cambridge Serial Total Energy Package (CASTEP) code.[19] The exchange–correlation potential was treated with the generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE),[20] PBE for solid (PBEsol),[21] and the local density approximation (LDA) in the form of Ceperley and Alder data parameterized by Perdew and Zunger (CA-PZ).[22,23] The Broyden–Fletcher–Goldfarb–Shanno (BFGS)[24] minimization scheme was used in geometry optimization. Vanderbilt type ultrasoft pseudopotentials[25] were employed to describe the interactions between ionic core and valence electrons. The considered valence atomic configurations had been set to be Si-3s23p2, Ge-4s24p2, and N-2s22p3. In the structure calculation, a plane-wave basis set with energy cut-off 500 eV was used for all cases. The k-points of 6×14×7, 6×13×7, 6×13×7, and 5×13×7 were adopted for the structures of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 by using Monkhorst–Pack mesh,[26] respectively. The system reached the ground state via self-consistent calculation when the total energy, the maximum displacement of ion, the maximum ionic Hellmann–Feynman force within and the maximum stress were less than 5×10−6 eV/atom, 5×10−4 Å, 0.01 eV/Å, and 0.02 GPa, respectively. In order to calculate electronic structures, the HSE06 hybrid functional[27] was used.
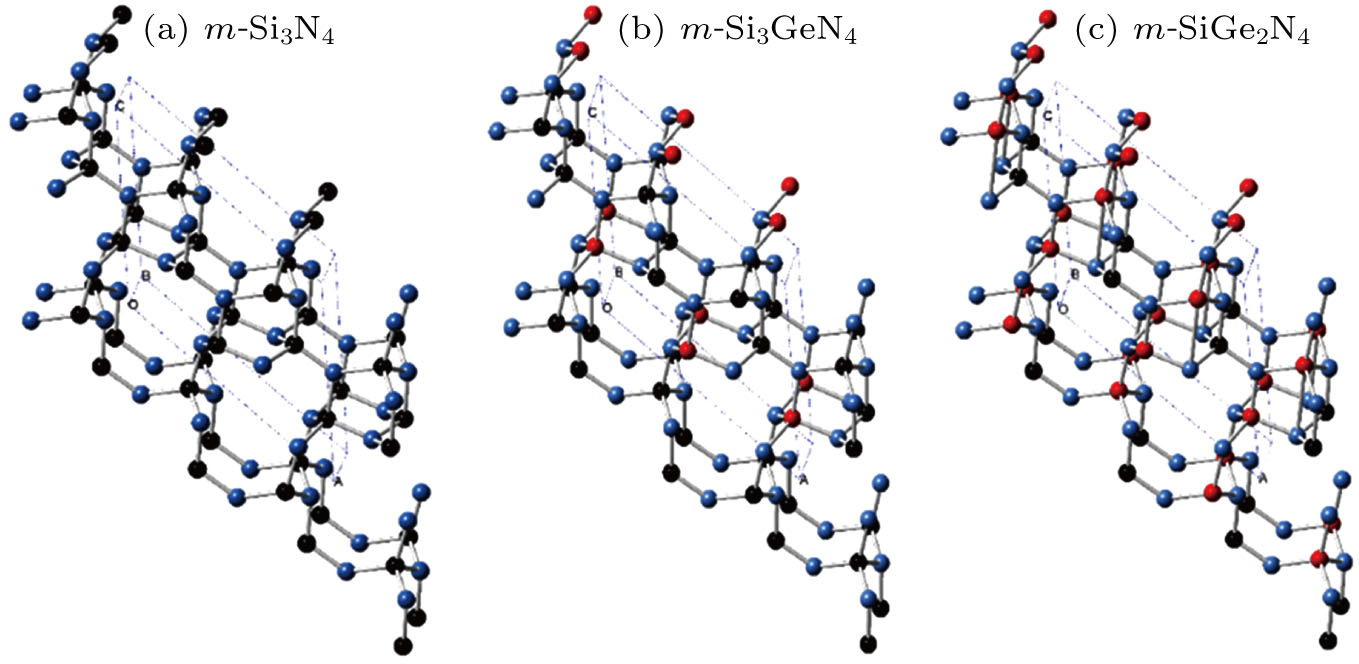
The crystal structures of m-Si3N4 and the double nitrides m-Si2GeN4 and m-SiGe2N4 are shown in Fig.
| Table 1.
Calculated lattice parameters (a, b, c in unit Å and β in unit degree) of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 compared with previous theoretical results. . |
Along with previous theoretical results for comparison, it can be seen that the calculated lattice parameters of m-Si3N4 and m-Ge3N4 are in excellent agreement with previous results.[13,15,16] The variations of the lattice parameters (a, b, c) with increasing the composition of germanium are shown in Fig.
 | Fig. 2. (color online) Calculated lattice parameters ((a) a, (b) b, and (c) c) of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 by PBE, PBEsol, and CA-PZ methods. |
The elastic constants are closely related to various fundamental mechanical properties of a crystal, which can provide, particularly, the information about the stability and stiffness of materials. For a monoclinic crystal, there are thirteen independent elastic constants, namely C11, C22, C33, C44, C55, C66, C12, C13, C15, C23, C25, C35, and C46. The calculated elastic constants of m-SixGe3−xN4 (x = 0, 1, 2, 3) are listed in Table
| Table 2.
Calculated elastic constants (in unit GPa) of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 compared with other calculated results. . |
It can be easily verified that the elastic constants of m-SixGe3−xN4 (x = 0, 1, 2, 3) satisfy their stability requirements, which indicates that they are mechanical stable. And the dynamic stabilities of m-Si3N4 and m-Ge3N4 have been verified by the phonon spectrum calculations in Refs. [13] and [14]. So it is revealed that m-Si3N4 and m-Ge3N4 are mechanically and dynamically stable via the elastic constants and phonon calculations. The elastic constants C11, C22, C33 represent the stiffness of the material when applying stresses along the x, y, z directions,[29] respectively. The obtained result obviously shows that all the m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 follow this ordering relationship: 
Furthermore, according to the Voigt–Reuss–Hill (VRH) average scheme,[30,31] the bulk modulus B and shear modulus G can be estimated using calculated elastic constants via the following equations:
The Young’s modulus E and Poisson’s ratio v are obtained from the following equations: 

| Table 3.
Calculated values of elastic modulus (in unit GPa), Poisson’s ratio v, percent compressibility of bulk modulus and shear modulus factors |
Poisson’s ratio v can be used as an indicator for ductility or brittleness. According to the Frantsevich’s rule,[34] the critical value that distinguishes between the ductile and brittle nature of material is 0.26. If 
The Debye temperature (









| Table 4.
Values of density (in units g/cm3), compressional, shear, and average sound velocities (in m/s) as well as Debye temperature (in K) for m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4.. . |
The elastic anisotropy analysis of a crystal is of great significance for understanding the mechanisms of material microcrack and durability in engineering science.[42] There are a variety of methods to quantity the anisotropy of a crystal structure, such as the universal anisotropic index 


For isotropic crystals, the percentages of elastic anisotropy for bulk modulus 











Simultaneously, the elastic anisotropic m-SixGe3 −xN4 (x = 0, 1, 2, 3) in Poisson’s ratio, shear modulus and Young’s modulus were investigated in the present work. The three-dimensional (3D) directional dependence and two-dimensional (2D) representation of anisotropy are calculated by utilizing the program of Elastic Anisotropy Measure (ELAM).[45] The vector direction (θ, ϕ) in the spherical coordinate system is used to describe the directional dependence of anisotropy, where θ (ϕ) represents the angle between the vector and the x-axis (z-axis) positive direction and they are expressed in radians. For an isotropic material, the 3D directional dependence would exhibit a spherical shape, while the deviation degree from the spherical shape reflects the content of anisotropy.[46]
The calculated 3D directional dependence of Poisson’s ratio and 2D representation in the (001), (010), and (100) planes for m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 is shown in Figs. 

 | Fig. 3. (color online) 3D directional dependence of Poisson’s ratio for (a) m-Si3N4, (b) m-Si2GeN4, (c) m-SiGe2N4, and (d) m-Ge3N4 at ambient pressure. |
The shear moduli for all possible directions of shear strain are also calculated. The calculated 3D directional dependence of shear modulus and 2D representations in the (001), (010), and (100) planes for the m-SixGe3−xN4 (x = 0, 1, 2, 3) are plotted in Figs. 





 | Fig. 5. (color online) 3D directional dependence of shear modulus for (a) m-Si3N4, (b) m-Si2GeN4, (c) m-SiGe2N4, and (d) m-Ge3N4 (d) at ambient pressure. |
The 3D directional dependencies of Young’s modulus for m-SixGe3−xN4 (x = 0, 1, 2, 3.) are plotted in Fig. 







 | Fig. 7. (color online) 3D directional dependence of Young’s modulus for (a) m-Si3N4, (b) m-Si2GeN4, (c) m-SiGe2N4, and (d) m-Ge3N4 at ambient pressure. |
Physical properties can be measured in different directions. Various crystal properties, including the elastic modulus, hardness, fracture resistance, thermal expansion coefficient, thermal conductivity, resistivity, and electric displacement vector, have different levels of anisotropy. If a physical property is closely related to orientation, it is anisotropic. Why does this reverse phenomenon appear? This is because of the different atomic arrangements and different atomic positions, and different atoms have different lengths in different directions, resulting in the fact that the physical quantities along the different directions possess different values. For m-SixGe3−xN4 (x = 0, 1, 2, 3), they have a monoclinic symmetry that belongs to the Cm space group, the symmetry of the monoclinic system is very low. Young’s modulus in Figs.
The electronic band structure reflects the law of the electron motion in a solid and determines the fundamental physical and chemical properties of material. The band structures of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 along some high symmetry directions of the Brillouin zone are calculated with HSE06 functional at ambient pressure, and the results are shown in Fig. 
 | Fig. 9. (color online) Electronic band structures of (a) m-Si3N4, (b) m-Si2GeN4, (c) m-SiGe2N4, and (d) m-Ge3N4 with the HSE06 hybrid functional. |
To further investigate the natures of the electronic band structure for m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4, the partial densities of states (PDOSs) are calculated as shown in Fig. 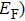

The structural, electronic, elastic, and anisotropic properties of the monoclinic phases of m-Si3N4, m-Si2GeN4, m-SiGe2N4, and m-Ge3N4 are investigated systemically in this work. The calculated lattice constants, elastic constants and elastic moduli of m-Si3N4 and m-Ge3N4 are in good consistence with previous theoretical results. The elastic constants of m-SixGe3 −xN4 (x = 1, 2) satisfy the stability criteria, which indicates that they are mechanically stable. According to the analyses of the obtained values of Poisson’s ratio v and B/G, it is found that only m-SiGe2N4 is ductile in nature. The densities of m-SixGe3−xN4 (x = 0, 1, 2, 3) increase whereas the Debye temperature 
The authors thank Q Y Fan (School of Microelectronics, Xidian University) for being allowed to use the CASTEP code in Materials Studio.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |