† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11304247 and 61505161) and the Shaanxi Provincial Research Plan for Young Scientific and Technological New Stars, China (Grant No. 2015KJXX-40).
We propose an identical geometrical representation scheme for both Landau–Zener (LZ) tunneling process in two-waveguide coupler with a cubically bent structure and stimulated Raman adiabatic passage (STIRAP) in three-waveguide coupler, similar to the geometrical representation of sum frequency process. The results show that although the two-waveguide coupler with a cubically bent axis has not aperiodic structure, it acts as a chirped quasi-phase-matching (QPM) grating and corrects the relative phase between the two supermodes in the curved coupler system. We present a scheme about how to choose the parameters to design the curved beam splitter.
Landau–Zener (LZ) non-adiabatic tunneling process and stimulated Raman adiabatic passage (STIRAP) have different physical mechanisms and have aroused wide interest during the past two decades. For instance, the former has been widely used in waveguide arrays,[1,2] electron transfer on insulating surface,[3] Bose–Einstein condensate,[4,5] Bose–Fermi mixture,[6] optical lattices,[7] radio frequency superconducting quantum interference,[8] preparation of quantum state,[9] coherent destruction of tunneling,[10] to name a few, while the latter has been used in waveguide optics,[11–13] population transfer in atomic and molecular physics,[14–18] Bose–Einstein condensate,[19,20] generation of terahertz pulses,[21] optical storage,[22] and so forth. Shore et al. have discussed the differences between the STIRAP in three-level atom system and LZ tunneling process in four-state model.[23]
Longhi proposed a simple two-waveguide device with cubically bent structure which can successfully mimic LZ tunneling process of a two-level atom system, and the results indicated that LZ tunneling efficiency is only about 55%.[24] Exploiting this dual-waveguide coupler, Dreisow et al. realized nearly 100% LZ tunneling efficiency and designed a beam splitter based on LZ dynamics in experiment,[25] but they did not indicate how to select the relevant parameters to design beam splitter. Using quasi-phase-matching (QPM) scheme,[26,27] Suchowski et al. successfully achieved nearly full conversion efficiency in sum frequency process under the undepleted pump condition, and they used Bloch vector to describe the process of optical sum frequency conversion intuitively.[28,29] In this paper, we discuss the similarities between coherent tunneling STIRAP-like equations of light in three-waveguide coupler, sum frequency adiabatic conversion equations, and LZ tunneling equations of light in curved two-waveguide coupler.
On one hand, by using the similarities between sum frequency equations and coupled equations of a three-waveguide coupler and the method proposed by Bloch[30] and Feynman et al.,[31] we construct Bloch geometric representation model of the three-waveguide system. From this geometrical viewpoint, we reanalyze the complicated behavior of light tunneling process in three-waveguide coupler. On the other hand, we analyze the similarity between sum frequency equations and LZ tunneling equations of a curved two-waveguide system, and this similarity allows a better understanding of the influences of spatial waveguide structure and phase mismatch. We find that this curved two-waveguide coupler can constantly adjust the phase difference between two supermodes in coupler system, like a chirped QPM grating, and finally it achieves arbitrary light intensity splitting ratio in left and right channels, providing that the appropriate spatial chirp coefficient is chosen. Furthermore, we give a parameter selection scheme about how to design a curved beam splitter. According to a more complex STIRAP three-waveguide system, we analyze another simpler two-waveguide system.
Under the undepleted pump condition, the sum frequency coupled equations can be simplified into[29] idÃ1/dz = κÃ3e−iΔkz and idÃ3/dz = κÃ1e+iΔkz, where κ is the coupling coefficient, Δk is the constant of phase mismatch, Ã1 and Ã3 are the complex amplitudes of signal and idler wave. Substituting Ã1 (z) = A1 (z)e−(iΔk/2)z and Ã3 (z) = A3 (z)e+(iΔk/2)z into the coupled equations, we can obtain
Equation (
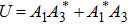
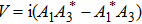
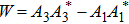
In a three-waveguide coupler system shown in Fig.
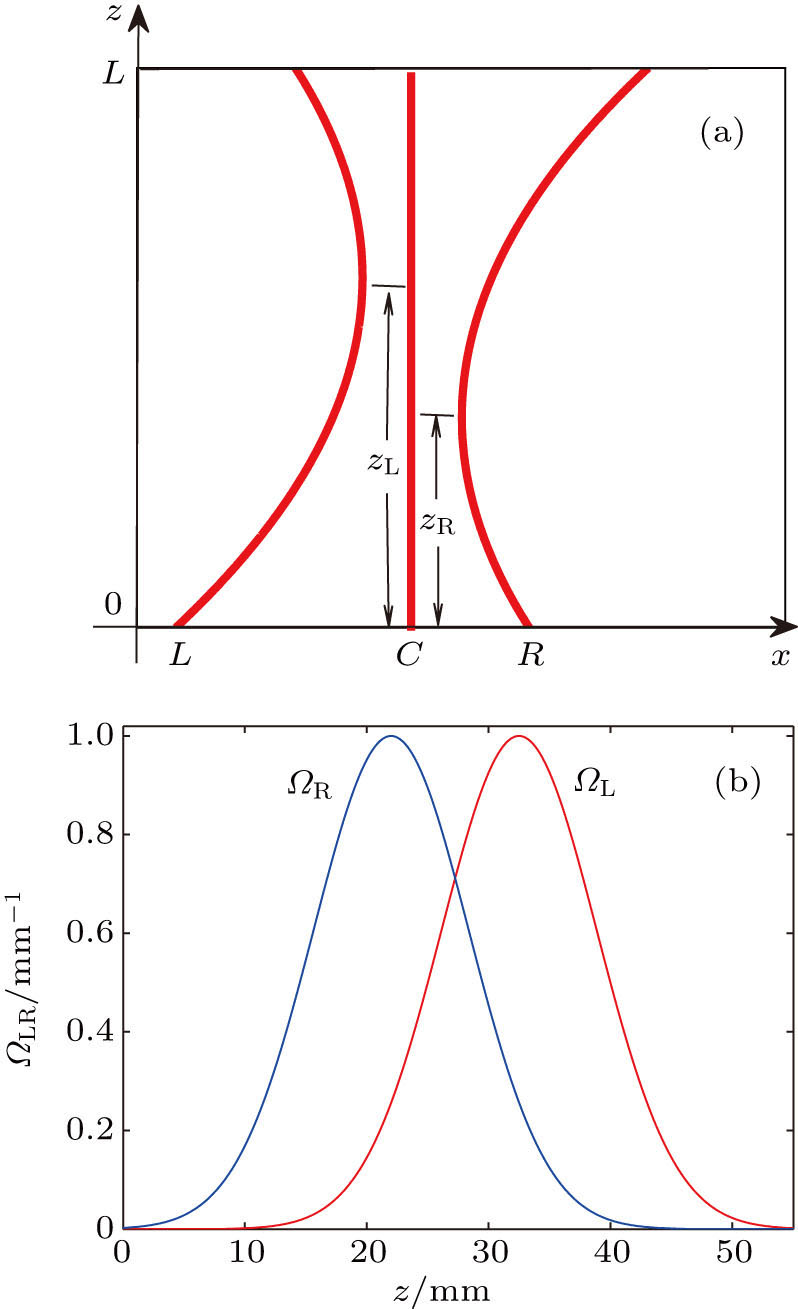 | Fig. 1. (color online) Schematic diagrams of (a) three-waveguide coupler and (b) the distribution functions of the tunneling rate versus propagation distance. |
The coupled differential equations for a three-waveguide system take the following form:[13]
Bloch vector B(z) = (U,V,W)T represents the energy relation in three-waveguide coupler. Equations (
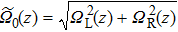
The dot represents the derivative with respect toz. During the STIRAP in three-waveguide system, the initial adiabatic state points along the state |Φ0 (−∞)〉 = |L〉, in order to maintain a continuous alignment of this adiabatic state with the trapped state |Φ0 (z)〉, the adiabatic tunneling condition shall be fulfilled, and the tunneling rate ΩR between the right and central waveguides must precede ΩL which is the tunneling rate between the left and central ones. Choosing proper tunneling rate distribution functions can adjust the mixing angle θ (z), and further control the proportion of light intensity in left and right waveguides.
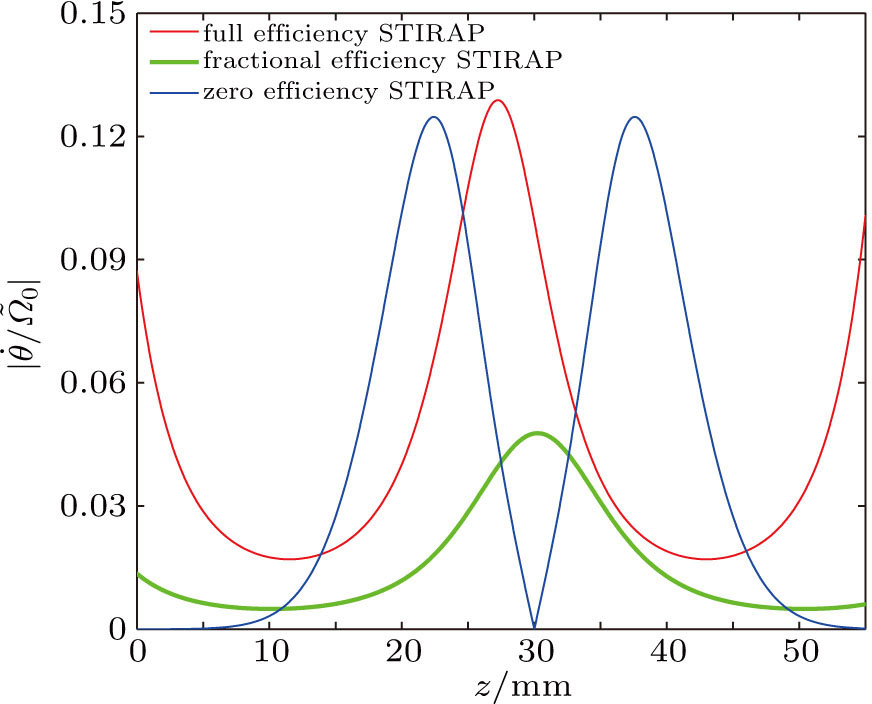
In the counterintuitive three-waveguide tunneling scheme, ΩR precedes ΩL. The initial mixing angle θ( -∞) ≈ 0, the initial dark state Φ0 ( −∞) = |L〉, then, as the propagation distance z approaches to infinity, θ( +∞ ) ≈ π/2, the final dark state Φ0 (+∞) = |R〉. Figure
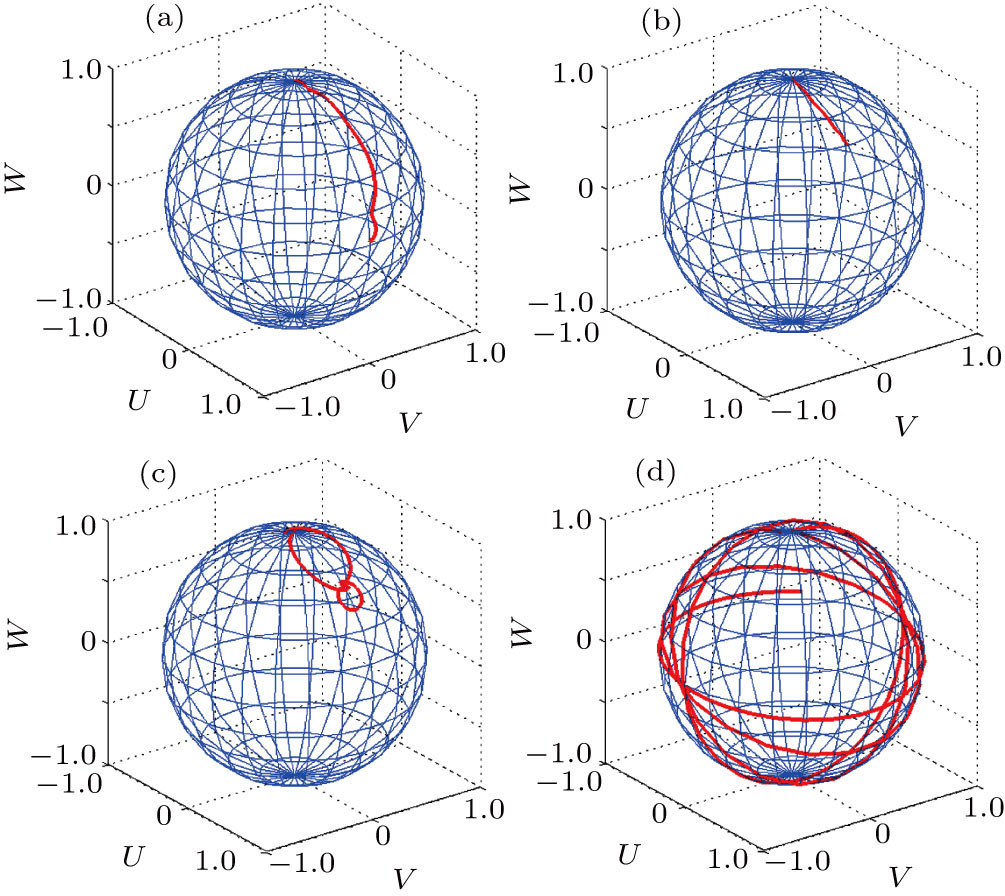 | Fig. 2. (color online) Geometrical visualizations of STIRAP in three-waveguide directional couplers: (a) full efficiency STIRAP, (b) fractional efficiency STIRAP, (c) zero efficiency STIRAP, and (d) non-adiabatic passage. In all of these schemes, the light is coupled into the left waveguide, and the selected adiabatic tunneling rate parameters are the same as those in Ref. [13]. While in non-adiabatic scheme, the parameters are zR = 30.5 mm, zL = 22 mm, ζR = ζL = 9 mm, Ω = 1 mm−1, 
|
In full efficiency STIRAP scheme, figure 


In fractional efficiency STIRAP scheme, ΩR still precedes ΩL. Unlike the STIRAP, with the propagation distance tending to infinity, ΩR = ΩL, these two tunneling rate distributions vanish together in the same proportion, and the Bloch vector B(z) rotates around one longitude in the WU plane as shown in Fig. 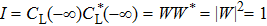
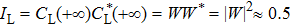
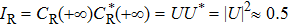
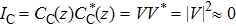
In a zero efficiency STIRAP scheme, ΩR precedes ΩL at very early distance, but vanishes more slowly than ΩL at very later distance, Bloch vector B(z) deviates from the longitude which is parallel to the WU plane, and finally it goes back to the starting point as shown in Fig. 
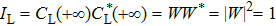
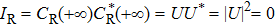
In the non-adiabatic scheme, the tunneling rate ΩL precedes ΩR, θ(−∞) ≈ π/2, the initial state vector is composed of two instantaneous eigenvectors |Φ+ (z)〉 and |Φ− (z)〉, i.e., 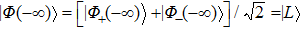
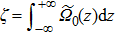
With angular velocity vector defined as Ω(z) = [−ΩL(z),0,−ΩR (z)]T, using the symmetrical characteristic of Eq. (
As in classical dynamics, a force Ω(z) × B(z) which is perpendicular to Bloch vector B(z) can change the movement of Bloch vector. Taking into account both the definition of the space-dependent mixing angle θ (z) and assumptions U = −CR (z), W = CL(z), the dark state Eq. (

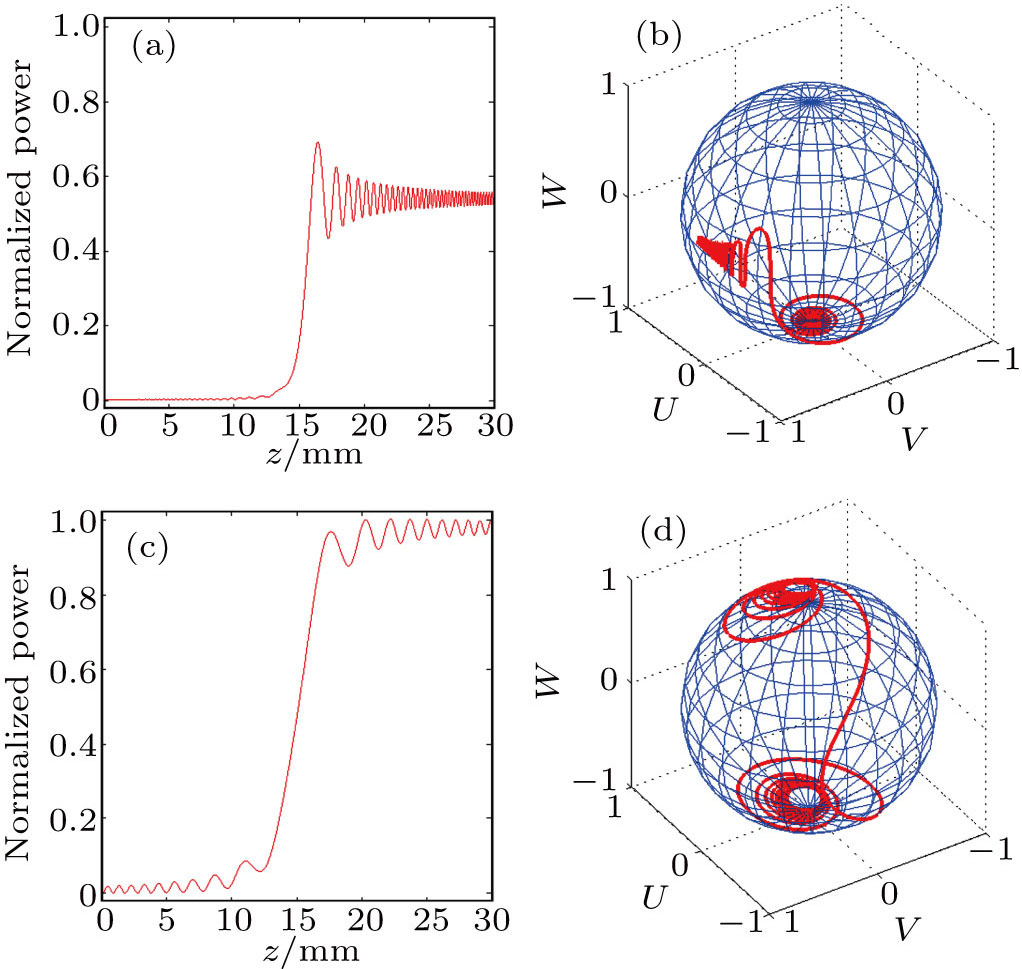
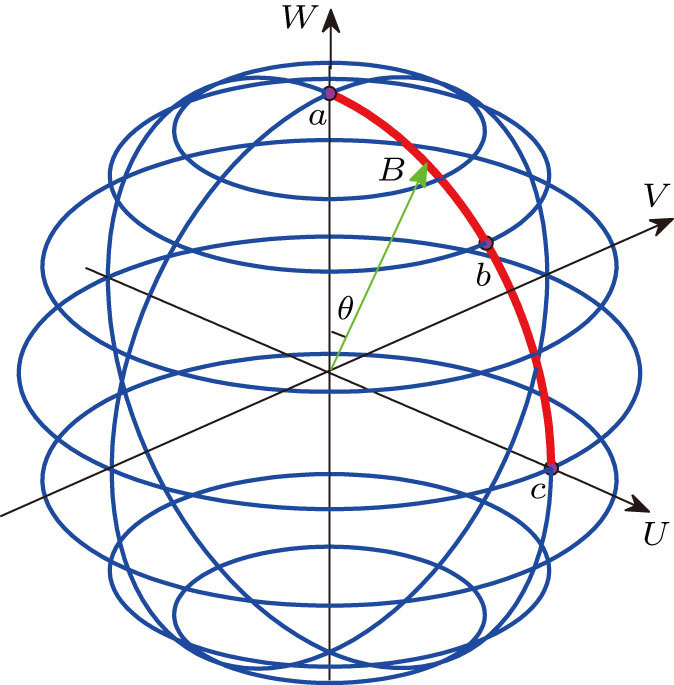 | Fig. 3. (color online) Geometrical representation of ideal STIRAP in three-waveguide directional coupler, the central waveguide is not excited. |
According to the resemblance between the three-waveguide coupled differential equations and the sum frequency coupled equations under the undepleted pump condition, we construct the three real-valued Bloch variables by using the three components of the light field complex amplitude. Expressions (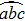
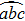
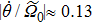
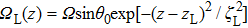
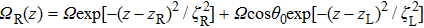
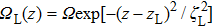
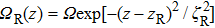
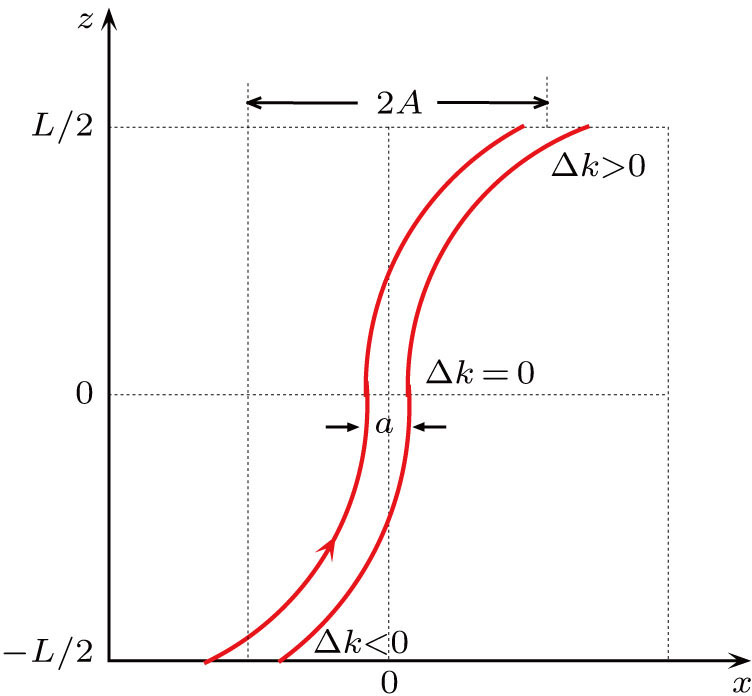
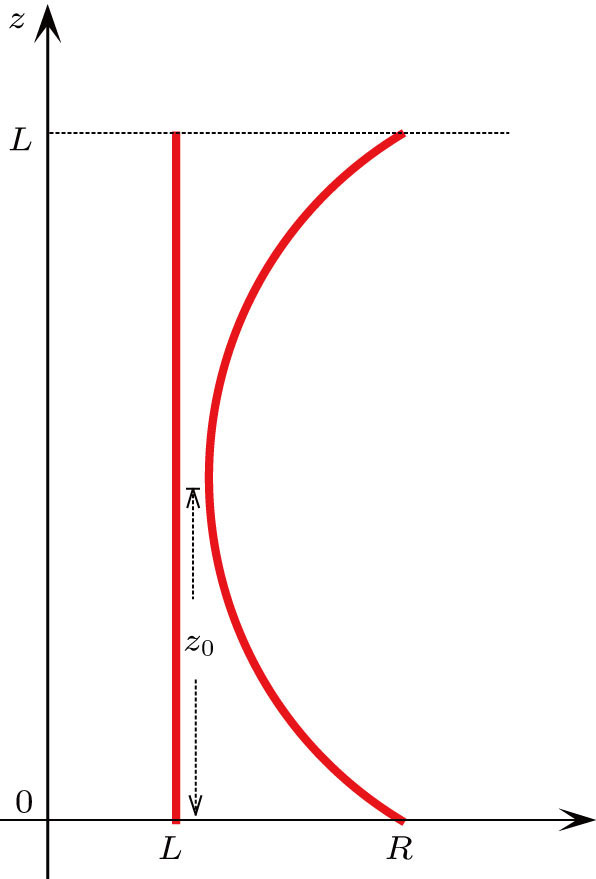
Longhi[24] proposed a cubically bent two-waveguide device to mimic LZ tunneling process of a two-level atom system as shown in Fig.
If we make the following substitutions: 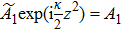
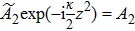
As indicated by Longhi, the coupling constant κ = 48πaAns/(λL3), where λ is the optical wavelength in channel and ns is the substrate refractive index. It is easy to see that κ is a positive constant proportional to A when other physical quantities are all fixed constants. However, as we borrow the chirped quasi-phase-matching (QPM) grating theory and further analyze the analogy between Eqs.(
There are two supermodes in the two-waveguide system, one is even supermode with the propagation constant β1 and the other is odd supermode with the propagation constant β2, and β1 > β2. When two channels are straight, at the input of the coupler z = 0 the initial phase difference ΔΦ = ΦR − ΦL = 0, so we have a constructive superposition in left waveguide and a destructive superposition in right waveguide. The beam power is confined in the left channel, because the two modes have different speeds. The phase difference ΔΦ between the right waveguide ΦR and the left waveguide ΦL varies with the propagation distance z, especially, at a certain distance, the phase difference ΔΦ = ΦR − ΦL = π, which means that we have a constructive superposition in the right waveguide and a destructive superposition in the left waveguide, the beam power tunnels into the right channel. The values of ΔΦ can take 2π, 3π, 4π, 5π,... with the spreading distance increasing. When ΔΦ takes an even number of π, the beam power stays in the left channel, when ΔΦ takes an odd number of π, the beam power stays in the right channel. The beam power hops between the left and right waveguides, like Rabi oscillation in a two-level atomic system. But when the two waveguides have a cubically bent structure, in three different cases: z < 0, z = 0, z > 0, the values of the new variable Δk = κz are negative, zero and positive, respectively. Different value distributions of Δk have a striking similarity to a chirped QPM grating. Although this particular structure has not an aperiodic structure, it can correct the relative phase between the two supermodes as a chirped QPM grating. Changing the parameters A, a and L, we can achieve 100% LZ tunneling efficiency or achieve an arbitrary light intensity splitting ratio in the left and right channels.
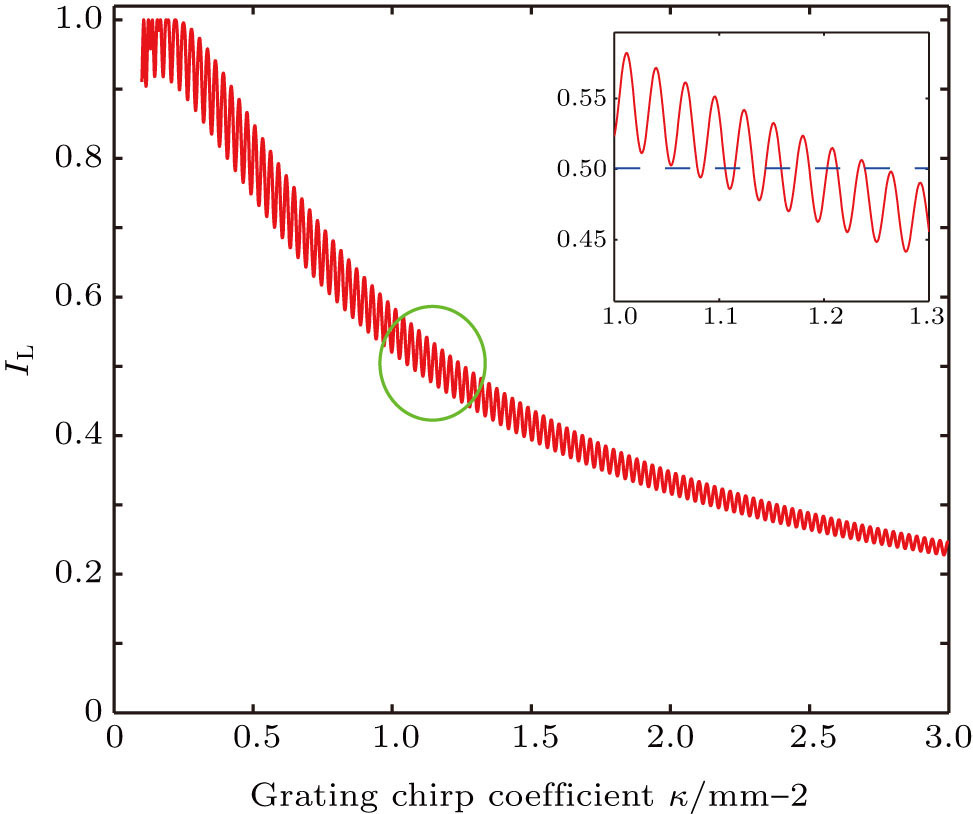
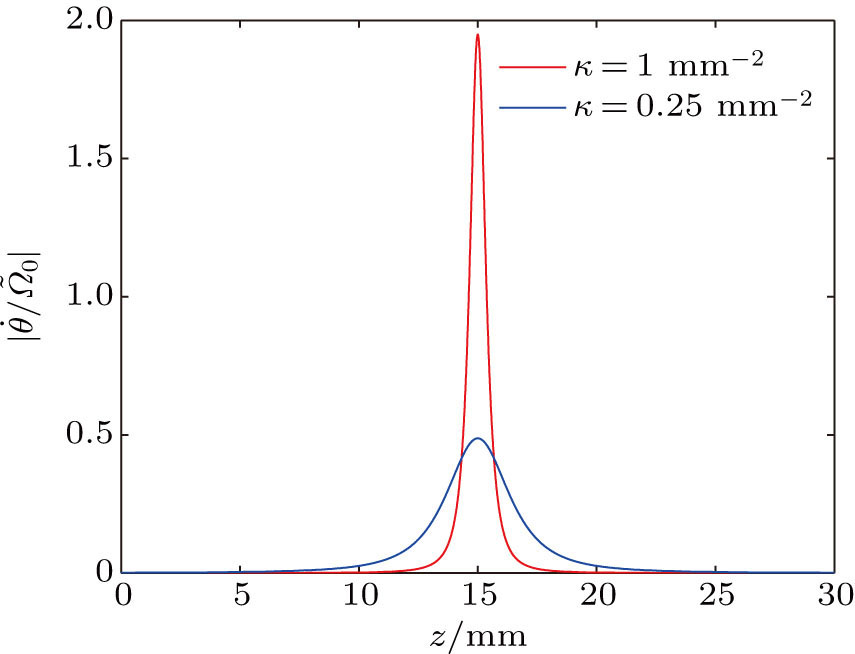
We choose Δβ = 1.013 mm−1, ns = 2.138, λ = 1.55 μm, a = 8 μm, and L = 30 mm to stimulate Eqs. (
As shown in Figs.
When the two waveguides are both straight, A = 0, κ = 0, the light intensity evolution along two-waveguide coupler is similar to Rabi oscillation in a two-level atomic system. To avoid this situation, we calculate the light intensity at the output port of left channel under the condition κ ≥ 0.1 as shown in Fig.
In the three-waveguide coupler system as shown in Fig.
We can see that LZ coupled equations (
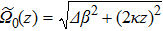
In the intermediate section of the curved dual-waveguide system, the condition 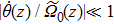

In this paper, first, we use the analogy between the equations of chirped sum frequency conversion and three-waveguide STIRAP to construct Bloch vector of three-state system, and under adiabatic or non-adiabatic condition, we describe the tunneling process of optical energy in the three-waveguide directional coupler by using Bloch vector. Then, after simple mathematical transformation, we find that the sum frequency process using a chirped QPM grating and LZ tunneling process in dual-waveguide with a bent axis bear an intriguing similarity. This particular cubically curved two-waveguide coupler can provide suitable chirp factor similar to a chirped QPM grating. By choosing the appropriate spatial chirp coefficient to correct the relative phase between two supermodes, we can control the distribution of light intensity in this curved two-waveguide system. For fixed wavelength λ, there exist different sets of parameters to design beam splitters with various sizes, and the parameters can be chosen very flexibly. Finally, based on three-waveguide coupler, we analyze another two-waveguide coupler which is based on resonant coherent tunneling principle.
During the past decade, STIRAP in multi-waveguide coupled systems has been studied in detail, so it is possible for us to learn something about a simpler curved two-waveguide coupler from a more complex three-waveguide system. In analogy with the three-waveguide Bloch equations, we can easily obtain the adiabatic condition of the curved two-waveguide without complex calculation steps, and this condition can help us to analyze the LZ tunneling process in a curved two-waveguide system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] |