† Corresponding author. E-mail:
Slow and fast light processes, based on both structural and material dispersions, are realized in a wide tuning range in this article. Coherent population oscillations (CPO) in electrically tunable quantum dot semiconductor optical amplifiers lead to a variable group index ranging from the background index (nbgd) to ∼ 30. A photonic crystal waveguide is then dispersion engineered and a group index of 260 with the normalized delay-bandwidth product (NDBP) of 0.65 is achieved in the proposed waveguide. Using comprehensive numerical simulations, we show that a considerable enhancement of slow light effect can be achieved by combining both the material and the structural dispersions in the proposed active QDPCW structure. We compare our developed FDTD results with analytical results and show that there is good agreement between the results, which demonstrates that the proposed electrically-tunable slow light idea is obtainable in the QDPCW structure. We achieve a total group index in a wide tuning range from nbgd to ∼ 1500 at the operation bandwidth, which shows a significant enhancement compared with the schemes based only on material or structural dispersions. The tuning range and also NDBP of the slow light scheme are much larger than those of the electrically tunable CPO process.
Light velocity control has become one of the most important topics in optical engineering. “Slow light” refers to a significant decrease in light velocity whereas “fast light” refers to its velocity greater than the speed of light in vacuum (c). Today, optoelectronics plays the most important role in modern communication and information technologies, whereas there still exist some challenges such as the ability to store an optical signal in the optical domain without converting to the electrical format or in brief the optical buffering.[1] By realizing optical buffers, there would be no need to optical/electrical/optical conversions[2] and as a result, routing delay will significantly be reduced due to the complexity of protocols, size, and power of the routers. Data packets' collision is one of the still remaining challenges in optical networks. To solve this, one needs a controllable amount of delay or advance. Therefore, we are interested in tunable speed for light signal. Tuning ability is a critical feature of slow light schemes and in general, the range in which light speed can be tuned is of great importance. Light signal velocity is the same as group velocity and has been defined by vg = ∂ω/∂k which can be expressed by [c − ω∂n(k,ω)/∂k]/[n(k,ω)+ω∂n(k,ω)/∂ω], where n is the real part of the refractive index and k is the propagation constant. Two terms in the group velocity relation are capable of controlling the group velocity. The first term is ∂n(k,ω)/∂k (structural resonances), also called waveguide dispersion which utilizes the frequency-dependent phase variation created by strong transmission or reflection characteristics, which results in a constant group index that cannot be tuned actively by the bias current. The second term, ∂n(k,ω)/∂ω (material resonances), also called material dispersion, utilizes the refractive index change created by a narrow resonance in the absorption or gain spectra of the medium. The later can be controlled and then tuned electrically or optically. On the other hand structurally engineered slow light demonstrates a very larger group index than that from the material dispersion method and then, is very effective in slow light generation. Initial experiments were based on electromagnetically induced transparency (EIT) to achieve a large group index (low group velocities). In an EIT scheme, a narrow transmission window is created due to the destructive interference between a strong pump beam and a weak probe one, therefore, a large group index can be obtained over this transmission window. Using EIT, the light velocity decreased to c/165 in a 10-cm lead vapor cell.[3] Later, by utilizing sodium atoms at low temperatures, group velocity decreased to 17 m/s.[4] Coherent population oscillations (CPO) is also utilized in an alexandrite crystal to realize a low group velocity of 91 m/s at room temperature.[5] When a strong pump field and a weak signal beam co-propagate in a semiconductor structure, the beating between these two fields causes the carrier density to oscillate. These oscillations then lead to the scattering of pump beam into the signal beam which in turn results in a refractive index change for the signal. Several schemes have been proposed to achieve a large delay-bandwidth product (DBP) including stimulated Raman scattering[6] and stimulated Brillouin scattering.[7,8] Also, the generated light is delayed compared with the reference using a four-wave mixing experiment in a hot rubidium atomic vapor.[9] On the other hand, structural resonances in photonic crystals (PCs) have been widely used to achieve the slow light effect. Due to the photonic band gap (PBG) property of PCs, the slow light phenomenon is investigated theoretically and experimentally near the Brillouin zone edge of the photonic crystal waveguide (PCW).[10,11] In addition, the problem of pulse broadening due to group velocity dispersion (GVD), reduces the peak intensity of a pulse[12] and thus makes it less effective for nonlinear applications. In general, a trade-off has to be made between the bandwidth and effective group index of the slow light.[13] Therefore, it is critical to linearize the dispersion relation of PCW over a large range, which corresponds to the regime of slow light with a wide band and low GVD, but more importantly, we also need to enhance the slowdown factor (ng) of slow light as much as possible. Very recently, a number of methods have been proposed to optimize the slow light features of PCWs, such as modifying the waveguide width,[14] varying the hole size,[15] adjusting the hole position,[16] changing the hole shape,[17] and varying the hole refractive index through infiltrating a liquid.[18] For appropriate optimization, the realization of slow light with enhanced group index, enhanced NDBP, and reduced GVD is required.
The aim of this article is to use both mechanisms simultaneously in the same device to achieve a large group index in a wide tuning range. This device should be compatible and easy to be integrated with other optical subsystems and should be also GVD-engineered and loss-engineered for practical applications. In Section
In the following subsections, a theoretical model is developed to investigate the effect of both waveguide and material dispersions on the total group index.
The 2D PC slab has been widely used for slow light generation due to the easy fabrication process and some excellent characteristics. This PC slab includes two types: the air holes in the dielectric slab and the dielectric rods in the air. The former exhibits a transverse electric (TE) band gap and the latter shows a transverse magnetic (TM) band gap.[19] The TM-like and TE-like polarizations can approximately be distinguished by observing whether an electric field is perpendicular to or parallel with the surface of the wafer, respectively. The waves whose frequencies are within the photonic band gap (PBG) cannot propagate through the structure, and as a result when these waves are incident on the PC, they will be rejected back due to the absence of the corresponding mode. The most important parameter for slow light generation is the group index ng which can be written as[20]
Ellipse shaped holes are probably one of the easiest air hole shapes for practical fabrication. The scheme showing this optimized PCW can be seen in Fig.
Realization of the CPO phenomenon in the QD medium can be described as follows. In the presence of an intense optical pump field with the photon energy adjusted to the transition energy of a two-level system, saturation of absorption occurs since the population of the lower state depletes. If a weak and slightly detuned signal beam is present as shown in Fig.
Coupled rate equations have been used for studying and calculating the optical properties and carrier dynamics of QD SOAs.[21,22] In our model, electrical current is injected into the barrier and the pump and probe beams are applied to the QD ground states as shown in Fig. 



Here, J is the injection current density, e is the unit charge, and A is the active region cross section. 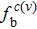


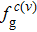

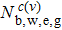
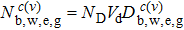


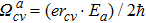
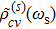
Then, the absorption coefficient, α(ωs), and the corresponding variation of the refractive index, Δn(ωs), of the signal beam can be obtained from the following equations:
We consider the optimized PCW slab geometry with QDs embedded in the core region of the structure as illustrated in Fig.
 | Fig. 3. (color online) Schematic diagram of the active QDPCW system. The purple shading illustrates the QDs in the waveguide region. |
As mentioned before, our approach involves the tailoring of both the material and structural dispersions. The engineering of the material dispersion curve involves the using of the semiconductor QDs under the CPO mechanism. The material dispersion at the probe wavelength is affected by the optical transition of the carriers of QDs. When the intense optical pump depletes the population of the QD ground state (GS), the absorption of the probe beam with frequency of ωs is saturated (transitions from the valence band GS to detuned conduction band GS). Since the pump and probe beams are slightly detuned, the population of the GS will oscillate. This population beating results in absorption reduction of the probe beam (a hole in the absorption spectra). By the Kramers–Kronig relation, the induced absorption reduction leads to a rapid index variation (the ∂n/∂ω term in the group velocity relation, which is known as the material dispersion).
On the other hand, the mechanism behind the designed waveguide dispersion assigned to the periodic PC structure can be explained as the fact that the holes form the boundary of the waveguide. The waveguide is narrow where there is a hole and is wider in the absence of holes. The described narrow-wide-narrow periodic geometry forms a Bragg mirror. Provided that the Bragg condition is fulfilled (i.e., λ/2 = na with a being the period of the structure), a standing wave is created. Otherwise, the light coherently scattered by the mirror plane forms an interference pattern along with the incoming light which moves slowly (proportional to ∂n/∂k). This term is also known as the structural dispersion.
Since the structural dispersion depends both on the geometry and on the background index and considering the fact that the material dispersion is proportional to the CPO process in QDs, both the material and structural dispersion affect the total index of the structure. It is difficult to calculate the group index analytically in this combined structure since both material and structural resonance are utilized simultaneously, as in general the waveguide dispersion features will be affected by the material dispersion. The group velocity can be calculated in such a PCW structure by assuming linear constitutive relations for the material. The H, as a harmonic magnetic eigenmode, is the solution to equation ω2/c2 = 〈H,ΘH〉/〈H,H〉 in which ΘH = ∇ × ε(r,ω)−1∇ × H. The group velocity (the derivative of ω with respect to k) can be expressed as[24]
Here, the Hellman–Feynman theorem has been considered. Regarding Maxwell equation ∇ × H = −i(ω/c)D and the Hermiticity of the curl operator and considering a low-loss dielectric, one may obtain the group velocity as
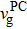

It is clear that the total group index depends linearly on the product of 
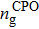

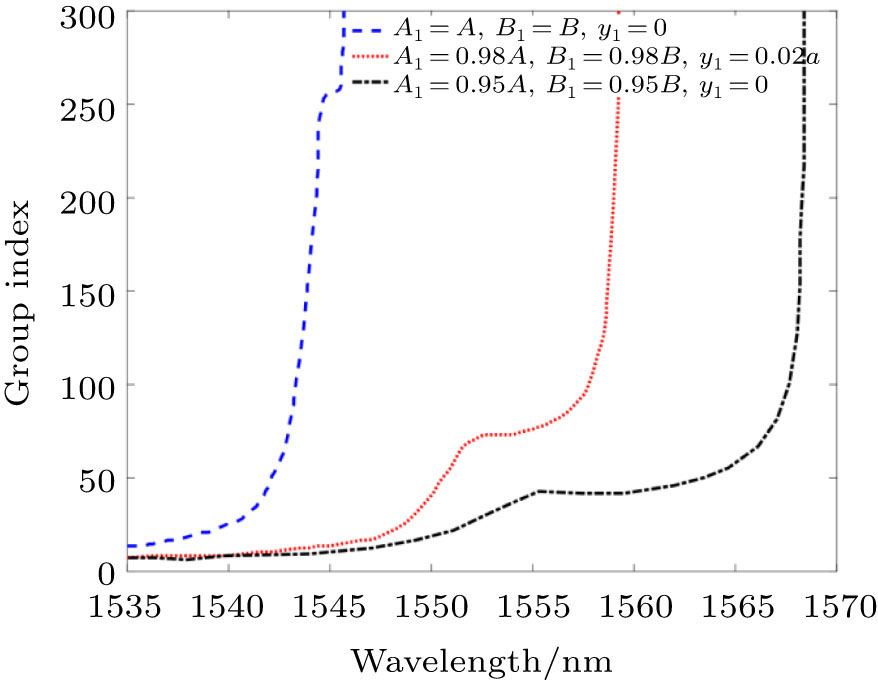
By simply adjusting the structural parameters in the PCW structure, flat and wideband slow light with a large ng is obtained. The group velocity dispersion also becomes zero since it benefits an S-shaped dispersion curve which prevents the signal from being distorted during propagation. A constant group index changing from 41 to 265 is obtained by optimizing the major and minor axes of the bulk elliptical holes and adjusting their positions and sizes in the first row adjacent to the defect (see Fig.
As depicted in Fig.
For the CPO-based slow light in OQ-SOA, we assume that the probe signal is a small signal. First, the coupled rate equations are solved to determine the bias condition of the SOA. Then, using density matrix formalism, small signal analysis for the signal beam is done and the CPO effects on the refractive index, absorption, and group index spectra are demonstrated and plotted in Fig.
 | Fig. 6. (color online) Variation of refractive index (top) creation of absorption dip (middle), and resulting group index (bottom) whereas nbgd = 3.4. |
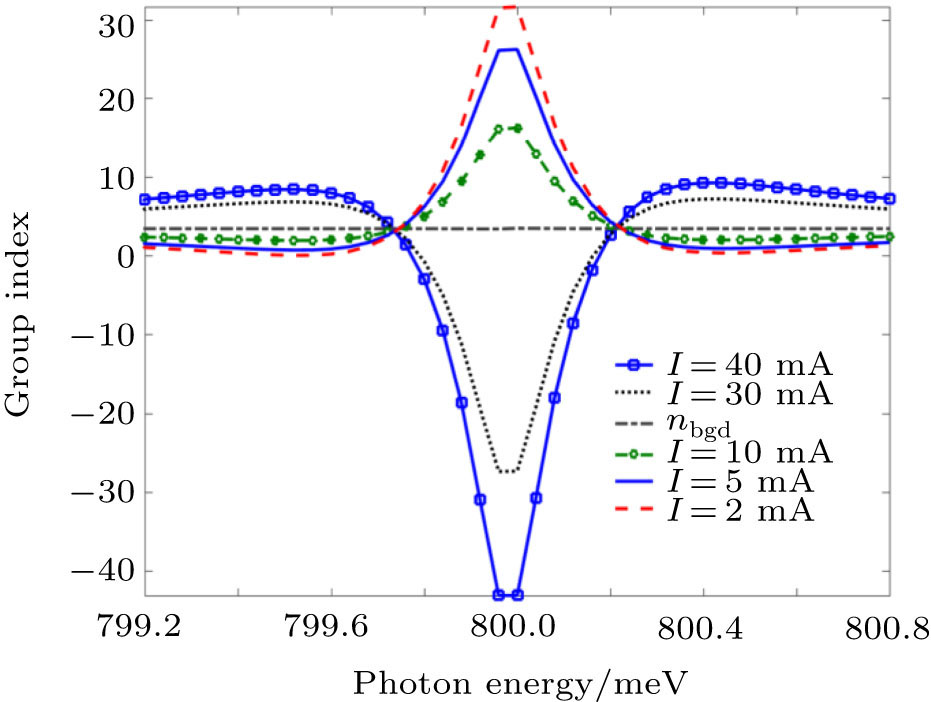 | Fig. 7. (color online) Controllable group index via CPO, both slow light and fast light (negative group index) are simultaneously achieved in QD-SOA by changing the bias condition of the SOA. |
It should be mentioned that the magnitude of the slow light and fast light increase by increasing the α factor of SOA. This can be understood by noting that the population pulsations in SOA create gain and index gratings. The pump and signal traveling through SOA scatter energy through these gratings. When the linewidth enhancement factor is very large, the contribution due to index gratings dominates which results in a large group index variation for the signal.
To investigate and compare the total group index, 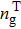

To give an acceptable justification for the pulse propagation in a diffractive medium such as the PCW structure, a full vectorial study of the electromagnetic fields is required. Therefore, a semi classical approach is used here for light-matter interaction where the FDTD method[27] is combined with the density matrix method to investigate pulse propagation in the QD slow light medium. In this case, propagation of the electromagnetic wave is affected by the microscopic polarization. Furthermore, the Liouville equation is numerically solved on FDTD grids considering the grid points of the QD carrier dynamics. The polarization density then enters into the Ampere’s law through the calculation of the expectation value of the macroscopic polarization. For achieving the FDTD results, at first, the group index caused by the CPO process (

For the CPO based slow light the tuning range is very small (from nbgd to ~ 30). It can be seen (from Fig.
A novel scheme is proposed for light speed control utilizing both material and waveguide dispersions simultaneously in the electrically pumped active QDPCW. We introduce a loss-engineered slow light waveguide which reduces the propagation loss and GVD by an appropriate waveguide design. A flat band slow light PCW is designed for the 1.55-μm operating wavelength, and a theoretical model is developed for the active QDPCW. It is found that the length and dimension of the active QDPCW can be highly integrated due to the significantly enhanced figures of merit of this novel structure. In brief, the slow-down factor ng, NDBP, GVD, and other slow light parameters may be significantly improved compared with those of the systems utilizing only material or structural resonances. This could be very important for realizing the efficient and tunable control of propagation of the pulses in compact semiconductor devices.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |