† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11504218, 11634008, 11674203, 11574187, 61108003, and 61227902), and the National Key Research and Development Program of China (Grant No. 2016YFA0301404).
Quantum entangled states, especially those having particular properties, are key resources for quantum information and quantum computation. In this paper, we put forward a new scheme to produce 31 continuous–variable (CV) tripartite entanglement fields based on three optical frequency combs via cascade nonlinear processes in an optical parametric cavity, and investigate the spectral characteristics of three frequency combs. The center wavelengths of the three combs are designed as 852 nm, 780 nm (atomic transition lines), and 1550 nm (fiber communication wavelength). The positivity under partial transposition (PPT) criterion, which is sufficient and necessary, is used to evaluate the entanglement in each group of comb lines. This scheme is experimentally feasible and valuable for constructing quantum information networks in future.
Quantum entanglement has been extensively applied in quantum information fields, such as quantum teleportation,[1] quantum dense coding,[2] and quantum key distribution,[3] etc. Diverse quantum entangled states have been studied intensively both theoretically and experimentally.[4–6] Generally, the continuous–variable (CV) bipartite entanglement can be generated in diverse systems, such as optical parametric amplifier (OPA) or optical parametric oscillator (OPO),[7,8] combination of two squeezed lights with a beam splitter,[9,10] and can be applied in different protocols of quantum communication.[11,12] In recent years, generating CV multipartite entangled states has been widely investigated in diverse methods, such as cascaded nonlinear processes,[13,14] dual-ported frequency doubling process,[15,16] and four-wave mixing process.[17–21] On the one hand, multipartite entangled states with different frequencies, especially including the fiber communication windows and the atomic transition lines, are more practical in applications of quantum communication networks and quantum storage. Such kind of three-color entanglement has been demonstrated both theoretically and experimentally in two cascaded NOPOs in 2012.[14,22]
On the other hand, quantum entanglement resources with high efficiency and multi-channel for quantum communication network is becoming a popular branch in quantum optics. The optical frequency comb is one of the ideal systems that can realize multi-channel and wavelength division multiplexing (WDM) for quantum communication network. In 2011, 15 quadripartite entangled cluster states were generated simultaneously in experiment via optical frequency combs.[23] A theoretical scheme to produce a multiplexed entanglement frequency comb in a nondegenerate optical parametric amplifier (NOPA) was proposed in 2013[24] and a low-frequency signal beyond the quantum limit was obtained via frequency-shift detection using frequency combs in 2015.[25] In addition, a large-scale cluster entangled state, which is necessary for usable quantum computation and quantum information processes, can also be generated by using an optical frequency comb. A cluster entangled state with more than 60 modes of a quantum optical frequency comb was achieved experimentally in 2014.[26] A theoretical scheme to produce CV cluster-state over the optical spatial mode was proposed in 2014.[27] The scheme of 11 entangled high-order transverse modes generated from an optical spatial mode comb was proposed recently.[28] The related research about the optical frequency comb have aroused many interests in theory and experiment. In this paper, we put forward a new scheme to produce 31 CV tripartite entanglement fields based on three optical frequency combs via parametric down-conversion (PDC) and sum-frequency generation (SFG) processes with a χ(2) crystal in an OPO, which pumped by two fields (1573 nm and 550 nm). The center wavelengths of three combs are designed as 852 nm, 780 nm (transition line of Cs and Rb atoms) and 1550nm (optical fiber communication wavelength), for practical CV quantum information network with both storage nodes and fiber transmission lines.
The arrangements of detail are outlined as follows: In section
The schematic of the system is shown in Fig.
The interaction Hamiltonian for the system is
Under the condition of perfect phase matching without any detuning, the quantum Langevin equations of motion for the three modes can be expressed as
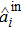
The operator equations of cavity mode âi (i = 1,3,5) after a single cavity round trip can be expressed as
After complex calculating, the fluctuations of intra-cavity fields can be given as
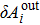


The definitions of the amplitude and phase quadrature fluctuations of output modes, input modes and vacuum noise are
The quadrature variances are defined by the following expressions: 
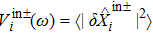

Here we consider that 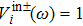

Actually, the whole bandwidth of the comb is confined by the phase-matching bandwidth of the crystal. The optical cavity can increase nonlinear coupling and lead to spectral filtering of the down-converted and sum-frequency output. For a bulk nonlinear optical crystal of length Lcrystal, the phase-matching bandwidth is approximately 10c/Lcrystal. The FSR of a cavity with length Lcavity is c/2Lcavity.[24,30] If we consider that Lcavity = 5.88 cm, Lcrystal = 1.96 cm, which are experimental feasible parameters, then 31 tripartite entangled states can be excited.
For Gaussian states, the complete information is available from the mean values (first-order moments) and the covariance matrix (second-order moments), of which only the latter is relevant for entanglement properties.[31] PPT criterion, which is sufficient and necessary conditions for bipartite splittings of Gaussian states with N modes with only a single mode on one side (1|N − 1), where N is the total number of entangled modes. The entanglement characteristic is checked by evaluating the symplectic eigenvalues of the partially transposed matrix.[32,33] In the tripartite scenario, the three possible 1 × 2 partitions have to be tested. All the partitions of the three mode states are inseparable when the smallest symplectic eigenvalue for each of the three partially transposed covariance matrices is smaller than 1. The smaller the symplectic eigenvalue is, the larger the entanglement becomes. Generally, the covariance matrix of the three modes can be written as

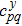
After the congruence transform ν′ = STνS, a new matrix ν′ can be obtained, where S represents the symplectic transformation.
Here, I1 is an identity matrix of 2 × 2. The partial transposition with respect to mode k corresponds to the change of sign of the phase quadrature. The covariance matrix of a state partially transposed with respect to mode k thus reads 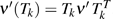
As is shown in Fig.
The smallest symplectic eigenvalues versus the pump parameter of PDC and SFG are shown in Fig.
In both Fig.
The tripartite quantum entanglement of the 0-order and the ±1-order comb lines are displayed in Fig.
Other schemes of combining frequency combs and nonclassical fields have been achieved in experiment.[23,26] To realize our scheme in experiment, it should satisfy the following conditions: choosing a nonlinear crystal with proper phase-matching bandwidth, making the conversion efficiency and the strength of nonlinear interaction of each tripartite entangled states balance, designing the optical cavity with appropriate structure and cavity length. In addition, the bandwidths of mirror coating should be wide enough thus the reflection and transmission are consistent for each tripartite entangled state. Based on our theoretical scheme, the corresponding experiment setup is simple, compact and feasible.
In summary, we theoretically propose a scheme to generate 31 CV tripartite entanglement states based on optical frequency combs, in which the central wavelengths are corresponding to the optical fiber communication line and the atomic transition lines. The sufficient and necessary criterion (PPT) is used to investigate the entanglement properties of 31 tripartite modes. Based on this work, with the technology of WDM, high efficiency and high capacity can be achieved for quantum communications and quantum dense coding. We hope that such an optical device and scheme might be useful to generate valuable entanglement resources for quantum communication and quantum information storage in real quantum information networks.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] |






