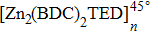† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61575096).
Utilizing the periodically structured metal–organic framework (MOF) as the reaction vessel is a promising technique to achieve the aligned polymer molecular chains, where the diffusion procedure of the polymer monomer inside MOF is one of the key mechanisms. To investigate the diffusion mechanism of fluorinated polymer monomers in MOFs, in this paper the molecular dynamics simulations combined with the density functional theory and the Monte Carlo method are used and the all-atom models of TFMA (trifluoroethyl methacrylate) monomer and two types of MOFs, [Zn2(BDC)2(TED)]n and [Zn2(BPDC)2(TED)]n, are established. The diffusion behaviors of TFMA monomer in these two MOFs are simulated and the main influencing factors are analyzed. The obtained results are as follows. First, the electrostatic interactions between TFMA monomers and MOFs cause the monomers to concentrate in the MOF channel, which slows down the monomer diffusion. Second, the anisotropic shape of the one-dimensional MOF channel leads to different diffusion speeds of monomers in different directions. Third, MOF with a larger pore diameter due to a longer organic ligand, [Zn2(BPDC)2(TED)]n in this paper, facilitates the diffusion of monomers in the MOF channel. Finally, as the number of monomers increases, the self-diffusion coefficient is reduced by the steric effect.
Future optical transmission system and optical information processing technology require a large number of optical waveguide devices with novel functions, and these functions mainly rely on optical materials with high optical anisotropy.[1,2] Among many optical materials, the fluorinated polymer materials feature their low optical loss, low-cost fabrication and packaging,[3,4] but their optical anisotropies are generally weaker. For a given molecular structure of fluorinated polymers, this weak optical anisotropy is mainly caused by the disordered alignment of the polymer molecular chains. Therefore, it has become a hot research topic to improve the degree of orientation of polymer molecular chains, thereby improving the optical anisotropies of materials.[5–9]
Utilizing the periodically structured metal–organic framework (MOF) as a reaction vessel is a promising technique to achieve the aligned polymer molecular chains, in which involved are three major steps, namely, the adsorption of monomers into the pore channels of an MOF, the polymerization of the adsorbed monomers, which subsequently yields oriented polymer chains along the channels, and finally the removal of the MOF to obtain highly-oriented polymer materials.[10,11] Compared with other methods,[6–9] the method of using the nanoscale-confined space of MOF as a reactor for monomer polymerization can control the tacticity of the polymer chain at a molecular level.[12] The key mechanisms to improve the polymerization orientation of monomers include the efficient adsorption and diffusion of monomers in MOF. Therefore, in constructing optically anisotropic fluorinated polymers, fundamental considerations are to study the diffusion characteristics of fluorinated polymer monomers in MOF, and to explore the relationship between monomer tacticity and monomer diffusion properties.
In the present article, we investigate the diffusion behaviors of the TFMA (trifluoroethyl methacrylate), the monomer of PMATRIFE (polytetramethylacrylate), inside two MOFs, [Zn2(BDC)2 TED]n (BDC = 1,4-benzenedicarboxylate, TED = triethylenediamine), and [Zn2(BPDC)2 TED]n(BPDC = 4,4′-biphenyldicarboxylate). Their all-atom models are established respectively by using molecular dynamics (MD) combined with the density-functional theory (DFT) and Monte Carlo (MC) method. Simulations are performed to study various factors influencing the diffusion behaviors of monomers in MOF, which include the electrostatic interactions between the monomers and MOF, the anisotropic shape of the one-dimensional (1D) MOF channel, the length of the organic ligand, and the number of monomers inside the MOF.
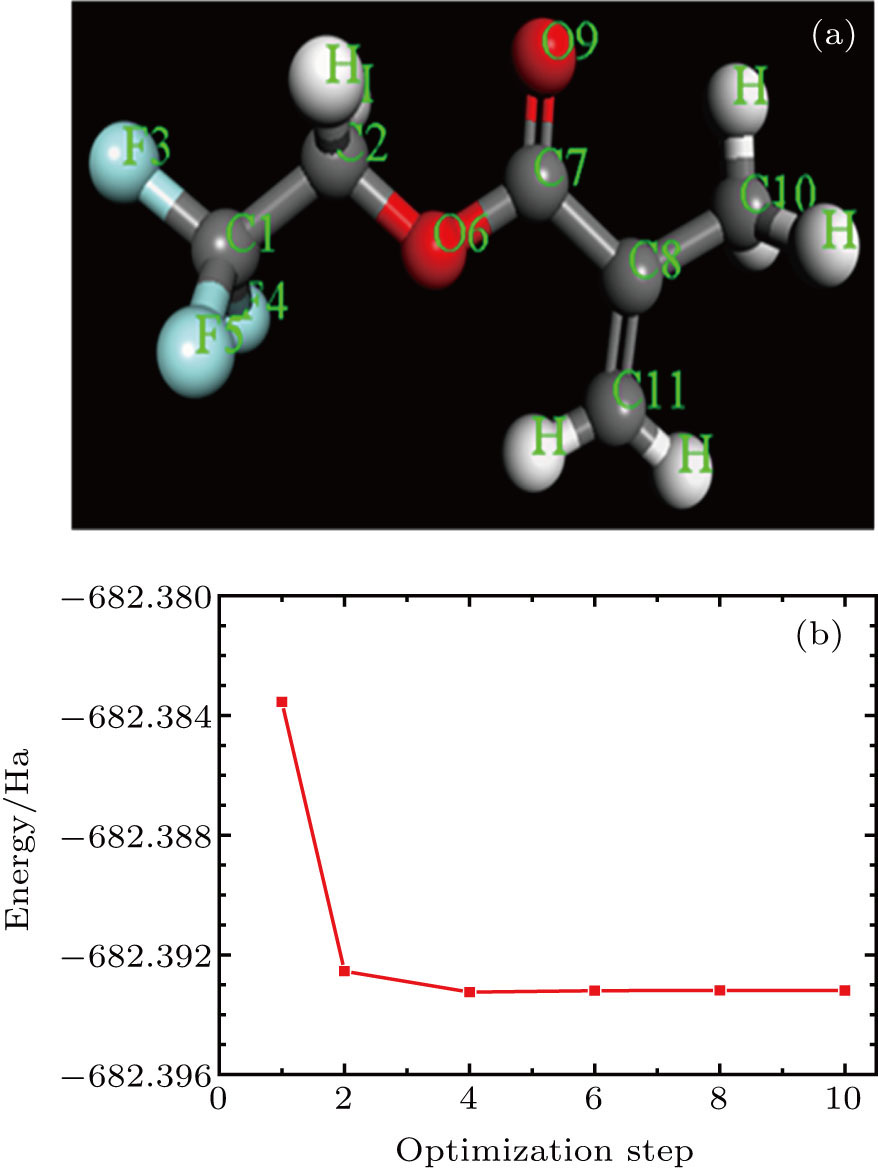
The initial structure of the TFMA monomer studied in this paper was obtained through the Cambridge Crystallographic Data Center (CCDC).[13] To ensure the rationality of the monomer unit in the MD simulation, it is necessary to perform the geometric optimization of the structural parameters of the initial TFMA monomer structure. In this paper, we used the software Material Studio to build and optimize the structure model. Parameters for geometric optimization were set as follows.[14] GGA\PBE was selected as the geometric optimization function; atom charge was selected for Mulliken analysis of charge distribution; and other parameters were set to be default values. The optimized molecular structure is shown in Fig.
In the present article, the all-atom MOF models of [Zn2(BDC)2(TED)]n with atomic charge distribution, and 

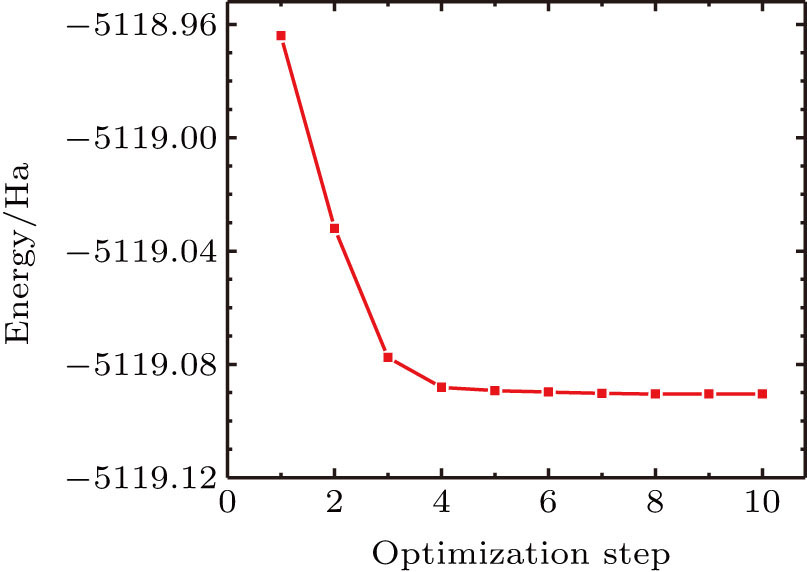
Considering the fact that the model constructions, optimizations, and diffusion simulation processes for these two MOFs, Zn2(BPDC)2 TED]n and [Zn2(BDC)2TED]n, are the same, [Zn2(BDC)2TED]n was taken below as an example to introduce these processes. The initial crystal structure of [Zn2(BDC)2TED]n used in this paper was also obtained from CCDC (CCDC-238860). Similarly, it was necessary to perform the geometric optimization of the initial structure model of [Zn2(BDC)2TED]n by using the DMol3 quantum mechanics module, in which the DFT was employed. The specific parameters were set as follows: the GGA\PBE function was selected as the geometric optimization function, atomic charge was selected for the Mulliken analysis of charge distribution, and other parameters were set to be default values. The optimized structure model of [Zn2(BDC)2TED]n is shown in Fig.
| Table 1.
Partial atomic charge distributions of the [Zn2(BDC)2TED]n model. . |
The structural models of 


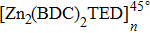
The self-diffusion coefficient Ds in units of m2/s can be calculated from the long-time behaviors of the mean-square displacement (MSD) of the atoms:[16,17]
For porous materials, the calculation formula for the self-diffusion coefficient can be further simplified. When particles collide in porous materials, the transition scenario occurs due to the effect of the confined space. The diffusion state is reached only when the particles can escape from the regional restrictions and traverse the entire periodic lattice. With a long-time diffusion behavior, the MSD curve is bent to a different slope, which eventually reaches a stable diffusion state and forms a linear relationship with time. Therefore, the differential in Eq. (
The simulation of the diffusion behaviors of the TFMA monomer was conducted in an MOF channel with 1 × 1 × 8 unit cells, among which 8 unit cells were in the direction of the MOF channel, and one unit cell was in the other two directions. The model is shown in Fig.
The entire MD simulation was composed of three phases in the following order: a high-temperature relaxation, an annealing, and a data acquisition.[18,19] Taking into consideration the material properties of the MOF itself, the parameters for the high-temperature relaxation were as follows: NVT was selected as the ensemble; the temperature was set to be 1000 K; atom-based computation was used for intermolecular interaction potentials for both electrostatic force and van der Waals force. Other parameters remained unchanged. After the high-temperature relaxation phase, the structure was annealed to a target temperature of 343 K, which was an experimental temperature of the polymerization. Then, the MD was carried out for the annealed systemic structure with TFMA monomers in the [Zn2(BDC)2TED]n channel. In this phase, the MD simulation with the NVT ensemble was conducted for 100 ps. The total simulation steps were set to be 105, and the step length was 1 fs. Both the electrostatic force and the van der Waals force were atom based, while the other parameters remained unchanged. After the MD simulation, this all-atom systemic structure reached an equilibrated state as shown in Fig.
 | Fig. 7. (color online) Systemic structure model of [Zn2(BDC)2TED]n containing 16 TFMA monomers after MD. |
The mean-square displacement curves of the TFMA monomers in (Zn2(BDC)2 TED]n,


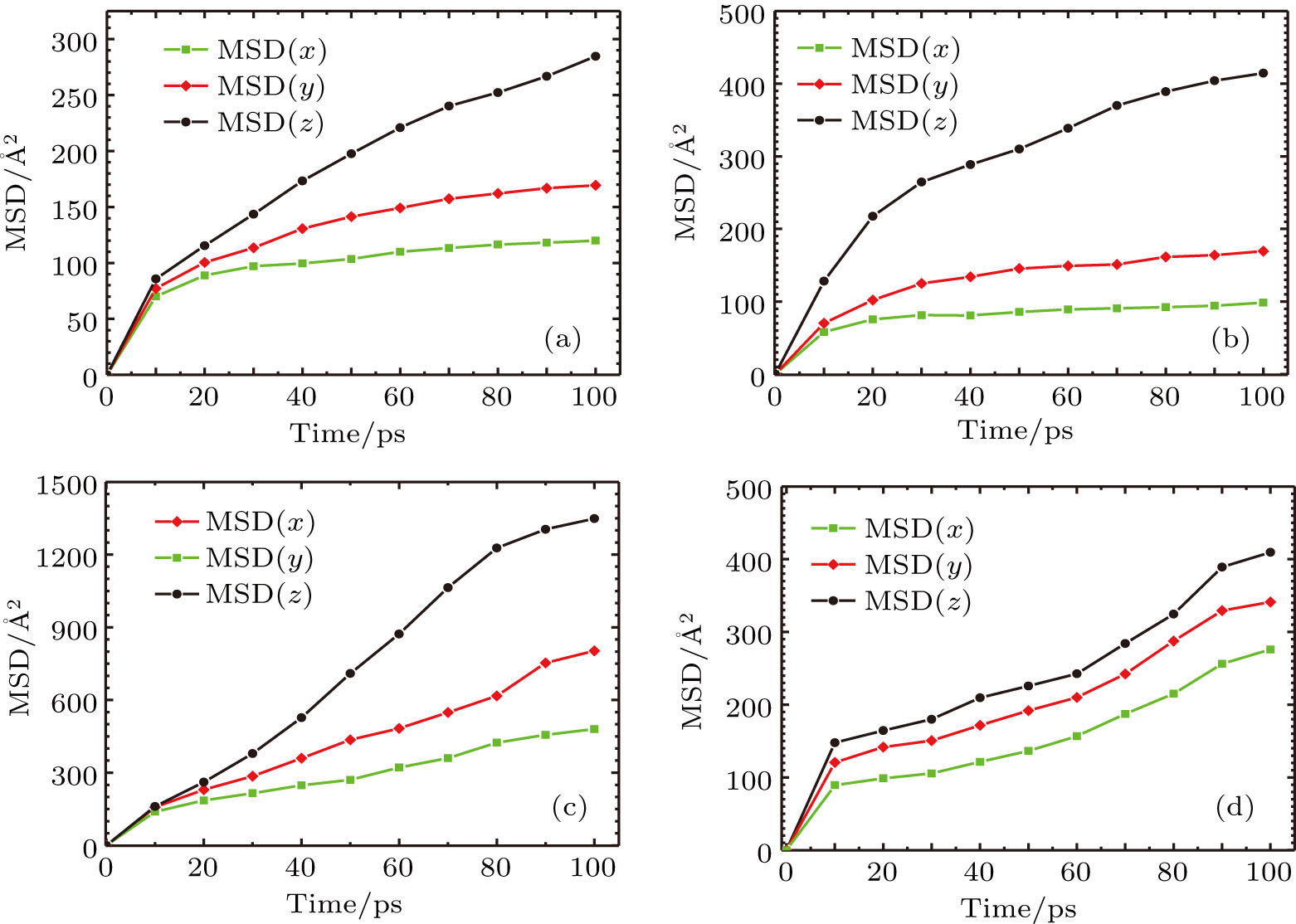 | Fig. 8. (color online) MSD curves of TFMA monomers diffusing in different directions for (a) [Zn2(BDC)2TED]n, (b) 

|
| Table 2.
Self-diffusion coefficients of TFMA monomer in different MOFs. . |
Based on the above simulation results, four factors influencing the diffusion of the TFMA monomer in MOF can be derived.
Table 


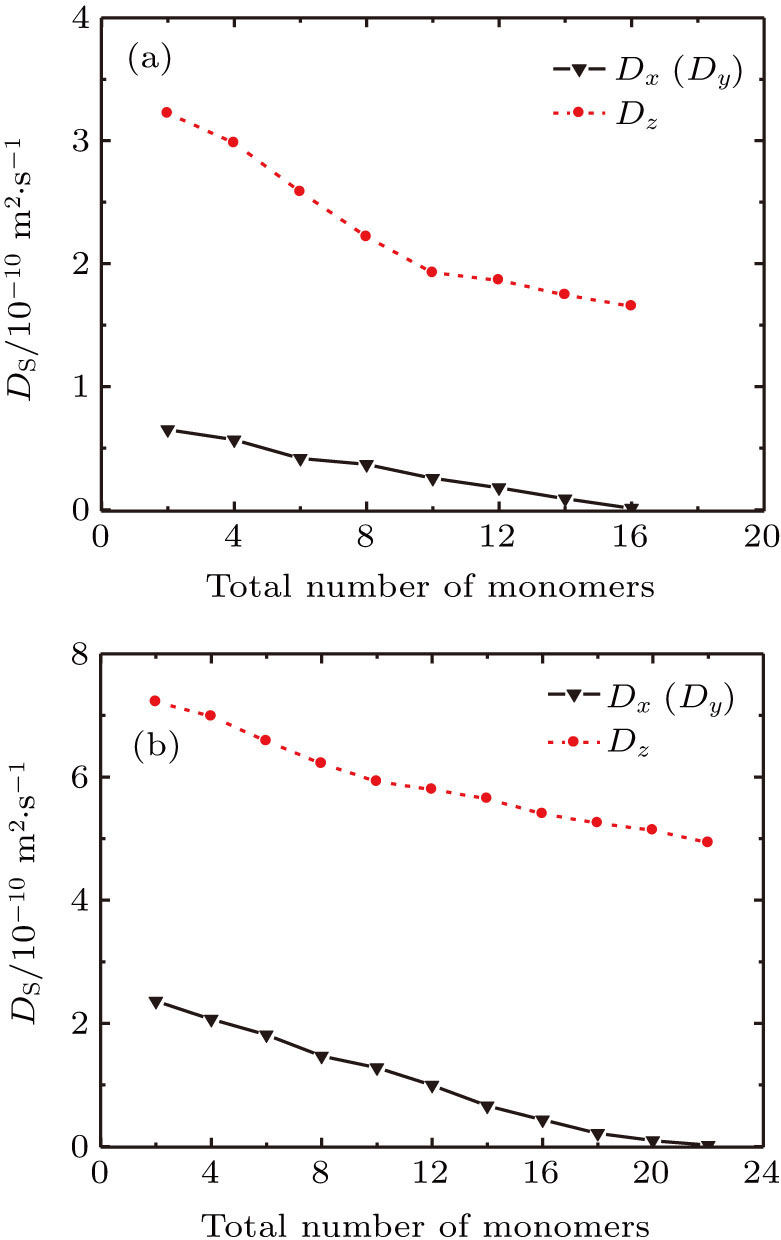
By comparing self-diffusion coefficients of the TFMA monomers in [Zn2(BDC)2TED]n and 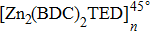
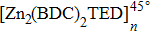
The comparison between self-diffusion coefficients of the TFMA monomer in [Zn2(BDC)2TED]n and [Zn2(BDC)2TED]n shows that in [Zn2(BDC)2TED]n with a slightly shorter BDC ligand, the self-diffusion coefficients of the TFMA monomer are a bit smaller. This is because the shorter organic ligand BDC results in smaller MOF channels, which restricts the free rotation of monomers, thereby affecting the diffusion of monomers. In the other case, the longer organic ligand BPDC results in larger MOF channels, which facilitates the diffusion of TFMA monomers in the channel.
Furthermore, the diffusion procedures of the TFMA monomers with different total numbers of monomers inside [Zn2(BDC)2TED]n were simulated and respective diffusion coefficients were calculated, as shown in Fig.
By utilizing the MD combined with DFT and MC, we performed simulations to investigate the diffusion behaviors of the TFMA monomers in [Zn2(BDC)2TED]n, 

The study of the influence of these four factors provides theoretical prediction methods of selecting the polymer monomers or MOFs,and controlling the orientation degree of polymer chains. These results are helpful in further investigating the effects of the absorption and diffusion behaviors of polymer monomers on the orientation of polymer chains in MOFs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] |