Wide band gap semiconductors are very important due to their large number of applications in optoelectronic devices like light emitting diode, optical wave guide, solar cells, solid state lasers, and photodetectors. The ZnSe is one of them which crystallizes in cubic zinc blend structure at ambient pressure. It has a distinct property of reversible transformation so it is being used in optical memory devices.^[1] Cd-dopped ZnSe ternary alloys are one of the II–VI semiconductor materials. They have high stability along with wide band gap^[2] and they are used for fabrication of photoluminescent, electroluminescent, photovoltaic, and photoconductive devices.^[3–6] Experimentally CdZnSe thin films have been prepared by vacuum evaporation,^[7] molecular beam epitaxy (MBE),^[8] electron beam pumping,^[9] electrodeposition,^[10] and chemical bath deposition (CBD).^[6] The experimental studies on CdZnSe have been done for structural properties,^[11,12] optical properties,^{[6,11,13–17]} dielectric properties,^[15] and magnetic properties.^[18]

The density functional theory (DFT) study on CdZnSe includes structural properties^[19,20] to measure lattice constants and bulk modulii; elastic properties^[21] to measure elastic stiffness constants; electronic properties^[19,20] to measure band gap energies; and optical properties^[20] to measure dielectric functions, refractive index, and extinction coefficient. But to our knowledge, there is no work found up to now about thermodynamical properties of CdZnSe. In the present study we fill this gap and study the thermodynamical properties of highly correlated ternary alloy Cd_0.25Zn_0.75Se with pressure range of 0 GPa–10 GPa and temperature range of 0 K–1000 K. The Cd_0.25Zn_0.75Se has direct band gap of 1.90 eV^[22] which corresponds to 652.6-nm wavelength. This material is useful in fabrication of light emitting diode capable to emit red light. The rest of the portion of visible spectrum may be explored with other ratio of composition of Cd and Zn in ternary alloy. In the highely corelated systems, the interaction of electrons with phonons are important which can give rise lattice distortions.^[23] As a result phonon frequencies may change and consequently thermodynamic properties will be affected. The thermodynamic properties of highly correlated systems should be calculated by using Coulomb repulsion parameter U,^[24] called Hubbard potential. The Hubbard potential is optimized by the method proposed by Gunnarsson et al.^[25] In this method, we used 2 × 2 × 2 supercell and hopping integral of d-orbital of central zinc atom is set to be zero. When atoms are considered to be embedded in a polarizable surroundings then the parameter U is the energy required to move an electron from one atom to another. So in this case U is equal to the difference of ionization potential (E_i) and electron affinity (E_a). Removing an electron from a site will polarize its surroundings, thereby lowering the ground state energy of the (N − 1) electron system.^[26] Thus E_i = E^N−1 − E^N and E_a = E^N − E^N+1, and the optimized value of the Hubbard potential is then U = (E^N−1 − E^N) −( E^N − E^N+1), where E^N±1 are the ground state energies of ( N±1)-electron system. The optimized value is used to calculate structural optimization of Cd_0.25Zn_0.75Se in WIEN2k code. The structural optimization data are then used to find thermodynamic properties of the ternary alloy.

This paper is organized as follows. Section 2 describes the computational details and results and discussions are presented in Section 3. The conclusion is given in Section 4.

The optimized calculations are performed by using DFT implemented in WIEN2k code^[27] with full potential linearized augmented plane wave (FP-LAPW+lo) method with local orbital. The generalized gradient approximation with Hubbard potential (GGA+U) is used as exchange–correlation functional where U = 2.3427 eV parameter is optimized by the method discussed in Section 1. The core and valence states are separated by −9.5 Ry (1 Ry = 13.6056923(12) eV) energy and the wave functions in the core for full potential scheme are expanded up to l_max = 10 in terms of spherical harmonics. The convergence criterion is set to be 0.00001e, 0.00001 Ry, and 1 mRy/Bohr for charge, energy, and force respectively, where R_MTK_max = 8.0. The RMTs are set at 2.17, 2.17 Bohr and 2.07 for Zn, Cd, and Se respectively. The K-point sampling is 11 × 11 × 11 in the full Brillouin zone.

The thermodynamic properties are determined by using quasi-harmonic Debye model which is implemented in Gibbs code.^[28] The energy volume optimization data are used as input to determine the pressure and temperature dependence of Helmholtz free energy, internal energy, entropy, Debye temperature, and heat capacity. In the quasi-harmonic Debye model the non-equilibrium Gibbs function G^*(V;P,T) can be written as^[29] 1 In this equation E(V) represents the total energy per unit volume of Cd_0.25Zn_0.75Se, P represents the hydrostatic pressure, is the vibrational Helmholtz free energy with θ_D/T = x which is a dimensionless parameter, n is the number of atoms per formula unit and is the Debye integral and is the Debye temperature, where B_s is adiabatic bulk modulus, σ is Poisson ratio and M is molecular weight per unit cell and is an explicit function.

The equilibrium geometry is achieved by minimizing the Gibbs function with respect to volume of the unit cell at constant pressure and temperature, i.e. 2

By using minimizing condition in Eq. (2), the vibrational contribution to heat capacity, entropy, internal energy, and thermal expansion coefficient can be computed and expressed as^[29] 3 4 5 6 where γ is Grüneisen parameter and B_T(p,T) = −V _T is the isothermal bulk modulus.

The bulk modulus is a numerical constant used to describe the elastic properties of a solid under pressure. It is a measure of ability of a substance to withstand the changes in volume under compression. It depends on pressure and temperature as shown in Fig. 1. From Fig. 1, we can see that the bulk modulus remains insensitive to temperature approximately up to 50 K and its value decreases with the rise of temperature. It is found that pressure has more pronounced effect on bulk modulus as compared to temperature. At absolute temperature its value is 59.09 GPa which close to the calculated values 62.37 GPa (LDA) and 49.40 GPa (GGA) in Ref. [19] but no experimental value is available in literature.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) The pressure and temperature dependence of bulk modulus.

The Helmholtz free energy is an important parameter to determine the stability of a structure. A structure with more negative value of the Helmholtz free energy will be considered to be more stable. The Helmholtz free energy at any temperature T can be written easily in the scope of standard thermodynamics as 7 Here Z represents the crystal configuration vector which consists of geometric information for crystal structure and E(Z) is the static energy. F_el represents the electronic contribution to free energy but can be neglected in the case of a semiconductor whereas F_vib is the vibrational contribution. The vibrational contribution in the Helmholtz and internal energies are related as 8 where S is the entropy. The pressure and temperature dependence of F_vib and U_vib are displayed in Fig. 2 and Fig. 3.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) The phonon contribution to the Helmholtz energy.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (color online) The phonon contribution to the internal energy.

The Helmholtz energy is decreased and the internal energy is increased with the increase of temperature and almost the internal energy is found to be insensitive to pressure above 200 K where the Helmholtz energy is increased on increasing pressure from 0 GPa–10 GPa. At low temperature limit, F_vib weakly depends upon pressure while at high temperature limit, it strongly depends on pressure whereas U_vib is found to be more sensitive to pressure at low temperature. At low temperature limit, the atomic oscillators have small amplitude of oscillations and hence an increase in pressure induces a prominent effect on the internal energy and insensitive to Helmholtz energy of the system. While at high temperature limit, pressure has negligible effect on the internal energy and prominent effect on the Helmholtz energy of the system because harmonicity is now converted into anharmonicity. The internal energy at 0 K is attributed to the existence of zero point motion and the calculated F_vib and U_vib at absolute zero is 12.01314 kJ/mol. The increase in Helmholtz energy on increasing pressure is attributed to decrease in entropy at certain temperatures. The effect of hydrostatic pressure and temperature on entropy of Cd_0.25Zn_0.75Se is shown in Fig. 4 which shows an increasing trend with the increase of temperature due to the increase of heat energy. At any temperature, the entropy of Cd_0.25Zn_0.75Se decreases with the increase of pressure due to the decrease in volume which consequently decreases the amplitude of vibration of atoms. Since anharmonicity of the system becomes very large at high temperature so the entropy is more pressure-sensitive.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) The phonon contribution to the entropy.

The Debye temperature is a key quantity in the quasi-harmonic Debye model which is related to many properties like elastic constants, thermal expansion, melting temperature, and specific heat. The Debye temperature at zero kelvin and zero Pascal is 428.10 K as shown in Fig. 5. This figure also displays the effect of temperature and pressure on Debye temperature which shows that it decreases on increasing temperature. When pressure is raised from 0 GPa–10 GPa then it increases. It should be noticed that Debye temperature is found to be more sensitive to pressure in comparison to temperature.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. (color online) The phonon contribution to Debye temperature.

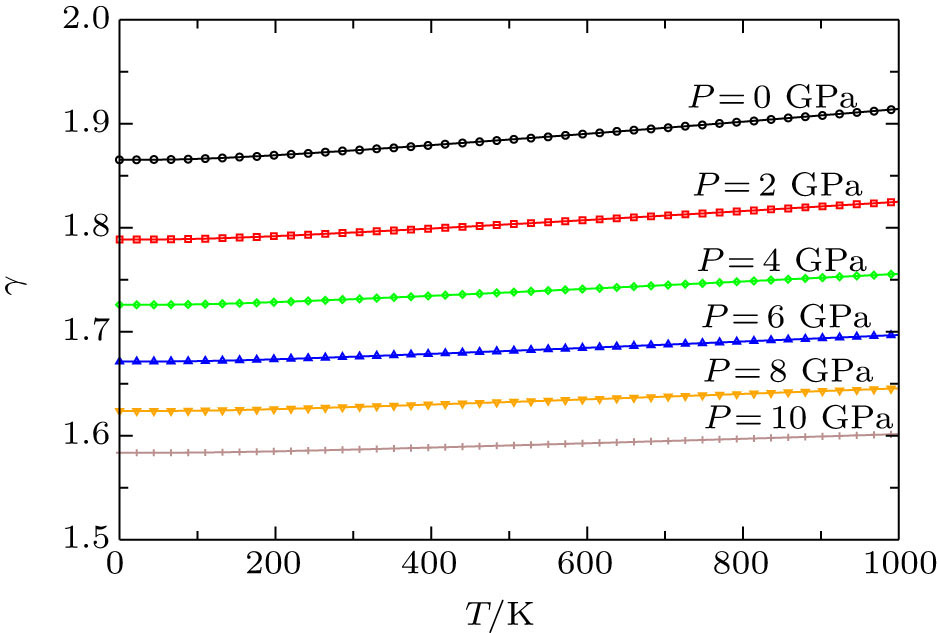
The Grüneisen parameter reflects the anharmonicity in the crystal that how much phonon vibrations are deviating from harmonic oscillations. Figures 6 and 7 show the Grüneisen parameter and thermal expansion coefficient as a function of pressure and temperature respectively. The value of the Grüneisen parameter and thermal expansion coefficient at room temperature and zero pressure is 1.874 and 1.838×10⁻⁵K⁻¹. It can be seen that both quantities decrease with increase of pressure. At low temperature the heat capacity obeys C_v ∝ T³ law which shows that more heat is absorbed at low temperature and hence the thermal expansion coefficient will rapidly rise in this temperature range. At high temperature limit the heat capacity becomes almost constant which means absorption of heat by material, so the thermal expansion coefficient is almost constant.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. (color online) The phonon contribution of Grüneisen parameter.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. (color online) The phonon contribution of thermal expansion coefficient.

The heat capacity at constant volume C_v and at constant pressure C_p on basis of Debye quasi-harmonic approximation as a function of temperature at different pressures is shown in Fig. 8 and Fig. 9 respectively. Since C_v approaches to Dulong–Petit limit at high temperature so it should be noted that C_v and C_p appear to be independent of temperature at high temperature and C_v is converging to the same value of classical limit of C_v = 74.19 J/(mol K). As this value is more than the value C_v = 3R at high temperature which shows the existence of anharmonic effects.^[30]

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. (color online) The pressure and temperature dependence of Cv.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. (color online) The pressure and temperature dependence of Cp.

Figure 10 shows the relationship of Helmholtz energy, internal energy, and entropy at T = 300 K relative to increase in pressure which is in agreement to Eq. (8). The decrease in entropy at room temperature (T = 300 K) at hydrostatic pressures of 2 GPa, 4 GPa, 6 GPa, 8 GPa, and 10 GPa is 5.0%, 9.7%, 13.2%, 15.8%, and 18.5% respectively. The decrease in entropy on the rise of pressure is due to the decrease in spreadness of energy.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. (color online) The pressure dependence of Helmholtz energy, internal energy, and entropy at T = 300 K.

The effect of pressure on Debye temperature and heat capacity at T = 300 K is shown in Fig. 11. The increase in Debye temperature at room temperature on increasing pressures 2 GPa, 4 GPa, 6 GPa, 8 GPa, and 10 GPa is 5.92%, 11.11%, 15.8%, 20.19%, and 24.15% respectively. The atoms in the solid under high pressure come close enough that equilibrium positions may disturb, creating a new physical system in which atoms of the solid at a given temperature vibrate with less amplitude as compared to in the equilibrium positions. As a result, the entropy and heat capacity decrease while the Debye temperature is a characteristic temperature of a material above which heat capacity becomes almost insensitive to a temperature, hence this Debye temperature will shift towards higher values under high pressures. Helmholtz free energy is a key quantity to describe the stability of structure and this shows that the stability of the structure decreases and hence Helmholtz free energy increases under high pressures. The internal energy almost remains constant.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. (color online) The pressure dependence of Debye temperature and heat capacities at T = 300 K.

The pressure and temperature dependences of thermodynamic properties of Cd_0.25Zn_0.75Se have been calculated by using FP-LAPW+lo method in the framework of DFT and Debye quasi-harmonic approximation which are implemented in WIEN2k and Gibbs codes respectively. The Helmholtz free energy, entropy, and thermal expansion coefficient are found to be more sensitive to pressure in high temperature limits while the internal energy is pressure-sensitive in low temperature limits. The specific heat at constant volume approaches to classical limit at T = 800 K. The Grüneisen parameter and thermal expansion coefficient decrease with the rise of pressure. This means that anharmonicity in our new material decreases and this material starts to expand at low temperature by increasing pressure on it.