† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51376101) and the National Natural Science Fund for Creative Research Groups, China (Grant No. 51621062).
Thermal optimization is very important for improving the performances of thermal systems. In engineering, the entropy generation minimization (EGM) has been widely used to optimize and evaluate the performances of thermal systems. However, the consistency between the EGM and the optimization objective should be specified when the EGM is used. In this paper, we discuss the view angle of irreversibility of entropy generation, and show that entropy generation directly reflects the exergy destruction or the ability loss of doing work. As the design objective in a thermal system is not often consistent with the view angle of irreversibility of entropy generation, the EGM may not lead to the optimal value of the design objective. In heat transfer and heat-work conversion, the inconsistence between the design objectives and the EGM is shown with some examples, and the applicability of the EGM is found to be conditional. The “entropy generation paradox” in heat exchanger analyses is also discussed, and it is shown that there is no direct monotonic relation between the minimum entropy generation rate and the best heat transfer performance of heat exchangers.
The design of the thermal system is very important for improving the system performance and reducing the cost.[1–3] For instance, the analysis and optimization design of the thermal control system are necessary because they are beneficial to the effective and steady operation of the spacecraft.[4] In the design of thermal power plants, the thermal processes should also be optimized to increase the output power.[5] Hence, this topic receives great attention from researchers.
In thermal optimizations, the concept of entropy generation is very often used because it can measure the irreversibilities of thermal processes. Many researchers have made contributions in this aspect. For instance, Li and Lai[6] optimized the performance of the ground heat exchanger with single U-tube by the entropy generation minimization method. Abbassi[7] applied the concept of entropy generation to the analyses of a uniformly heated microchannel heat sink. Baytaş[8] discussed the entropy generation for the natural convection in an inclined porous cavity. A lot of interesting and important results had been obtained when the concept of entropy generation was used.
On the other hand, it has been shown that the entropy generation minimization (EGM) does not always lead to the best system performance.[9–14] In heat exchanger analyses, the “entropy generation paradox”[9] is a well-known example. It was found that the heat exchanger effectiveness does not always increase with reducing entropy generation rate or entropy generation number. In refrigeration systems, Klein and Reindl[10] found that minimizing the entropy generation rate does not always result in the same design as maximizing the system performance unless the refrigeration capacity is fixed. In the analyses of an air conditioning system for room heating, Cheng and Liang[11] found that the EGM does not always lead to the increase of the heat flow rate into the room.
Therefore, it is worth making more efforts to discuss the role of EGM in thermal optimization. In this paper, the view angle of the irreversibility of entropy generation is analyzed, and the applicability of the EGM to the thermal optimizations is discussed. Some examples on heat transfer and heat-work conversion are also presented.
Irreversibility is an important characteristic of physical process in nature, which results in the symmetry breaking and the unidirectionality of time. Therefore, for any system with fixed boundary conditions, we can find a function that varies monotonically with time when an irreversible process happens. This function is called the Lyapounov function[15] and can be used to measure the irreversibility. In “From Being to Becoming” by Prigogine,[15] it was pointed out that the criterion of the Lyapounov function is that the positive or negative symbol of the derivative of the function with respect to time must be different from that of the function itself. For instance, for a closed system with fixed temperature and pressure, the Gibbs free energy satisfies the criterion, so it is the Lyapounov function and the time arrow of the system. For a closed system with fixed temperature and volume, the Helmholtz free energy is the Lyapounov function.
From the above, it can be seen that we could have different Lyapounov functions for the systems with different boundary conditions. Even for the same system, the criterion of the Lyapounov function does not refuse two or more ones, which means that we may have different Lyapounov functions for one specific system as long as the functions satisfy the criterion. These functions may be different projections of the irreversibility from different view angles. Obviously, the view angles of irreversibility for the Gibbs free energy and the Helmholtz free energy are different. Therefore, the discussion on the view angle of the Lyapounov functions is necessary for understanding the characteristics of the functions.
As is well known, entropy is a Lyapounov function of the isolated system, and is also widely used to measure the irreversibilities of physical processes. This concept was introduced by Clausius when he investigated the Carnot cycle in 1854.[16] The expression of entropy is
In thermal science, entropy was first introduced in analyzing the Carnot cycle, and the main view angle of irreversibility of entropy generation may be related to heat–work conversion although entropy has been applied to many other thermal problems. To simplify the problem, we can analyze a steady system here. With Eq. (
In thermal engineering, the concept of entropy generation is taken as an important tool to optimize the system performance in many cases. As the decrease of entropy generation means the decrease of irreversibility, it is believed that the entropy generation would decrease with increasing system performance. However, researchers have shown that the concept of entropy generation does not take effect in this way sometimes.[9–14]
In practical applications, the system performance may mean different objectives, such as the maximum heat transfer rate,[18] the maximum heat exchanger effectiveness,[13] the minimum average temperature of the heated domain,[19] the maximum output power,[20] the maximum COP of the heat pump systems,[21] etc. When the system performance maximization is consistent with the EGM, it is very sure that the decrease of entropy generation will lead to the performance improvement. On the other hand, if the performance maximization and the EGM lead to different targets, the EGM may not be applicable for improving the performance. In other words, the best system performance may not need to correspond to the minimum irreversibility measured by entropy generation. Whether a parameter can be used to evaluate the performance of a system depends on its consistency with the design objective of the system. This rule also holds true when the EGM is used to evaluate thermal systems and should be paid enough attention to. In the following, some heat transfer and heat–work conversion problems will be taken for example to explain the point in detail.
In a pure heat transfer process without work interaction, heat is only transferred for heating or cooling objects. There have been many different design objectives in practical applications, such as the system mass minimization,[22] the homogenization of temperature field,[4] the heat transfer rate maximization,[18] the heat transfer temperature difference minimization,[18] etc. It is very obvious that these objectives are not always consistent with the EGM because they are not related to the exergy destruction or the ability loss of doing work. Therefore, the irreversibility minimization from the viewpoint of entropy generation will not always benefit the design objectives. Some simple examples are presented below.
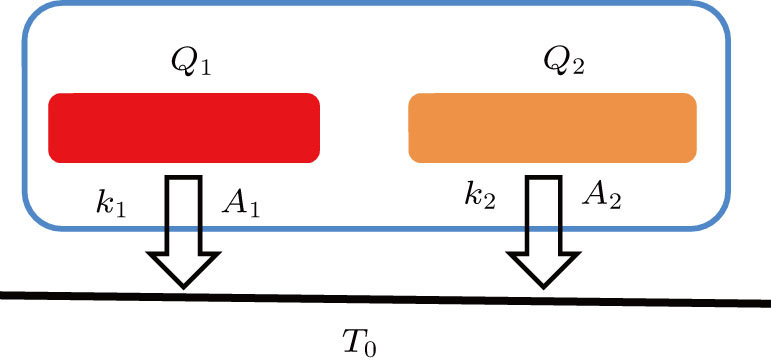
In the system shown in Fig.
Considering the heat transfer law, we have
If we use the concept of entropy generation to analyze the process, we have
Comparing the distribution results shown in Eqs. (
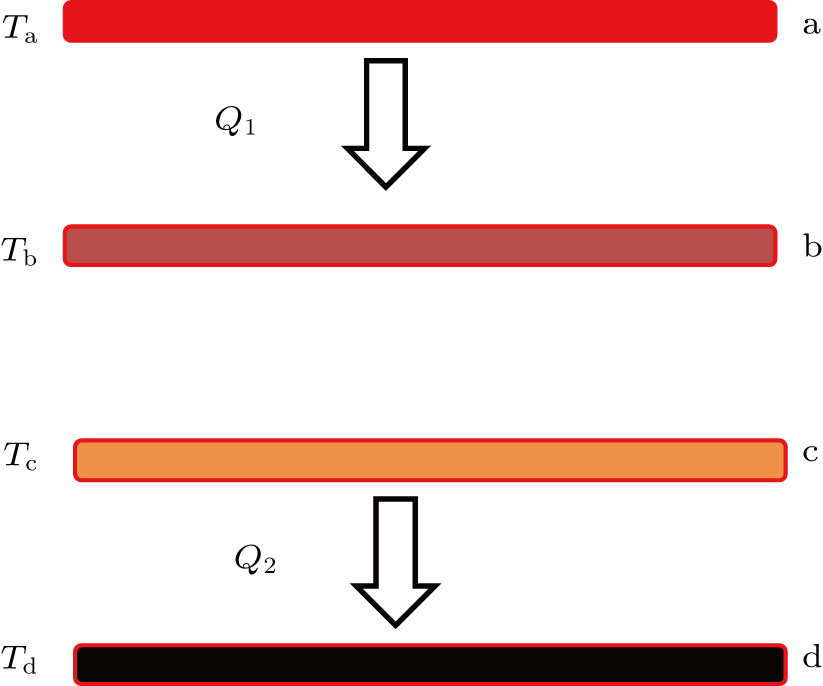
As shown in Fig.
First, we consider a case in which the heat transfer temperature differences are Ta − Tb = Tc − Td and the heat flow rates are identical, i.e., Q1 = Q2. It can be seen that the thermal resistances are also the same. Therefore, from the viewpoint of heat transfer, the performances of the two processes are the same. However, if we calculate the entropy generation rates of the processes on the assumption that Ta > Tc, we have
The difference between our objective and the EGM can also be found in the case in which sg−1 = sg−2 and Q1 = Q2. From the viewpoint of entropy generation, the irreversibilities and the exergy destruction rates of the two processes are the same. However, if we calculate the heat transfer temperature differences, we can find that
As shown in Fig.
 | Fig. 3. (color online) A two-stream heat exchanger.[24] |
The heat transfer rate and the effectiveness are
From Eqs. (
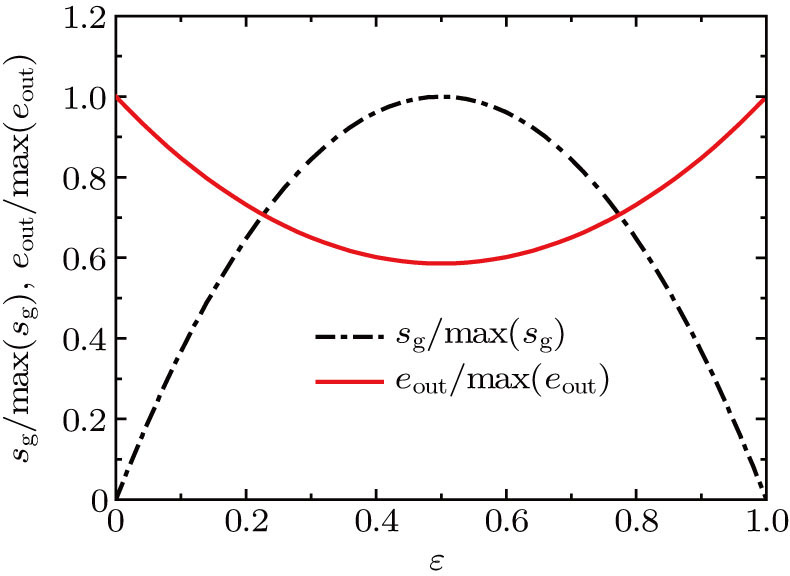
When analyzing the balanced counterflow heat exchanger with zero pressure-drop irreversibility, Bejan[9] first noted that the entropy generation rate or entropy generation number does not decrease with increasing ε when ε ∈ [0, 0.5]. Instead, the entropy generation rate or entropy generation number increases and reaches its maximum value at ε = 0.5. This behavior of entropy generation was called “entropy generation paradox”. Bejan[9,25] explained that the origin of this paradox was clear and that the “entropy generation maximum” (at ε = 0.5) associated with it is of little practical consequence[9] and the “paradox” disappears if one considers the effect of heat exchanger size not on the heat exchanger alone, but on the whole energy system in which the heat exchanger is an organ.
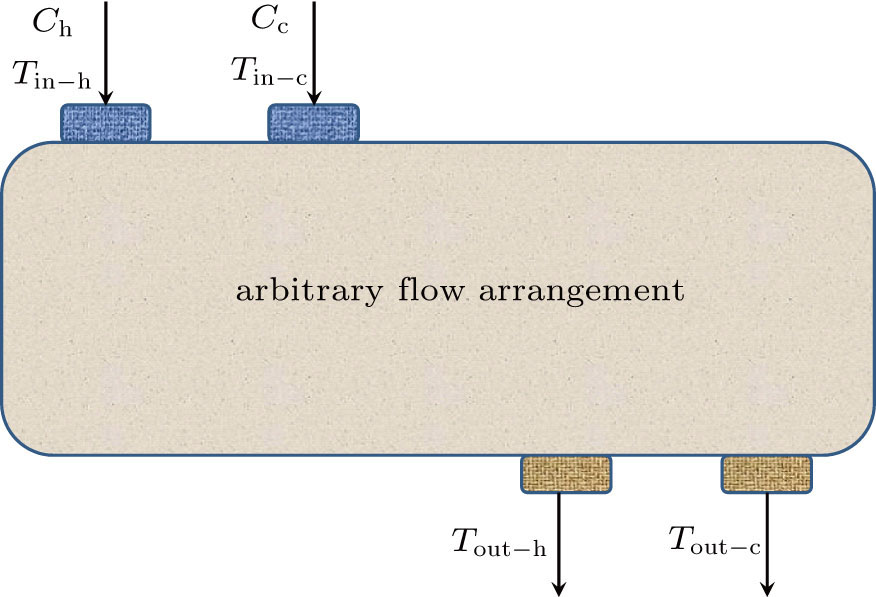
However, as a performance evaluation parameter, the consistency between the parameter and the optimization objective is necessary. The variation tendency between EGM and the effectiveness does not follow this rule when ε ∈ [0, 0.5]. For a heat exchanger with arbitrary flow arrangement shown in Fig.
It is shown in Eq. (
As below, a numerical example with zero pressure-drop irreversibility is presented. Assume that Ch = Cc = 1 W/K, Tin−h = 500 K, Tin−c = T0 = 300 K. The inlet exergy flow rate into the system is fixed because the inlet parameters of the streams are fixed. From Eq. (
In heat–work conversion, we also may have many different design objectives, such as the output power,[20] the thermal efficiency,[32] the thermoeconomic performance,[33] the COP of heat pump systems,[21] the heat flow rate into the high temperature heat source in heat pump systems,[21] etc. Some of them may be consistent with the design direction of the EGM, while some may be not. So, the applicability of the EGM also needs further investigating.
Equation (
Here, we come to discuss another precondition. Researchers showed that the entropy generation rate associated with dumping the used streams into the environment must be taken into account in the analyses of the power plant besides the entropy generation rate in the heat exchangers.[9] Other research[20,32,36] also showed that the entropy generation associated with dumping the used streams into the environment should be considered, otherwise the EGM will not lead to the maximum output power. However, this precondition may be fictitious because the used streams may not be dumped into the environment in practical applications. The thermal energy in the used streams can be used in many ways. It even can be stored in some phase change materials. So, the question is why the fictitious precondition should be satisfied? Considering Eqs. (
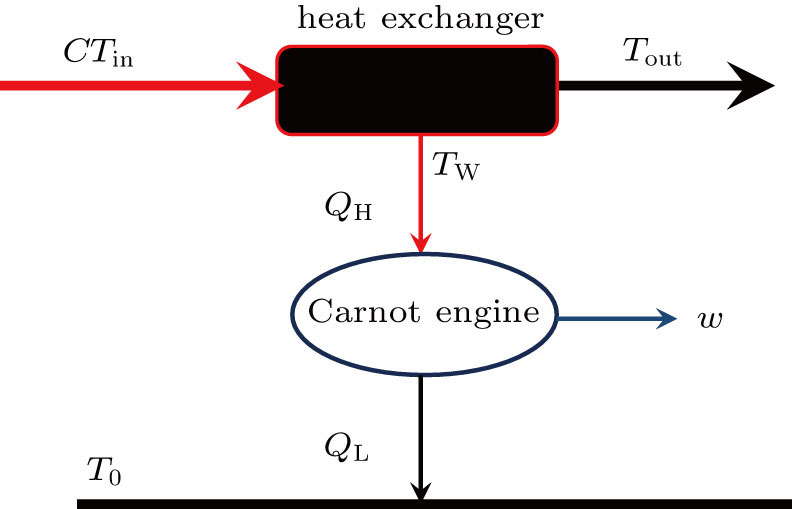
As shown in Fig.
The practical entropy generation rate is
 | Fig. 6. (color online) Variations of the entropy generation rates, the output power and the remaining exergy flow rate with wall temperature of the heat exchanger. |
In addition, if the inlet parameters are not fixed, which means that the exergy flow into the system is not given, we have already proved that the EGM does not lead to the maximum output power even if the virtual entropy generation rate associated with dumping the used streams into the environment is considered.[32] In such a case, the EGM does not correspond to the maximum output power either, which can also be understood mathematically with Eq. (
For other design objectives, the inconsistence between the entropy generation and the objectives has also been noted.
When the thermal efficiency was taken as the design objective, the work of Wang et al.[37] showed that the EGM does not always lead to the largest thermal efficiency in the endoreversible Carnot cycle. The same conclusions were also obtained when we analyzed the one-stream heat exchanger networks[32] and the combined endoreversible Carnot heat engines.[33] When the thermoeconomic performance was taken as the design objective, it was also proved that the EGM may not be applicable.[33]
For heat pump systems, the COP and the heat flow rate into the high temperature heat source can be our objectives. For the two objectives, research showed that the applicability of the EGM is also conditional.[21,38] The effects from different heat transfer laws were analyzed,[38] and the conclusions still hold.
From the discussion above, it can be seen that the design objectives of heat–work conversion systems may not always be consistent with the irreversibility measured by entropy generation. Reducing the irreversibility from the viewpoint of entropy generation may reduce the exergy destruction or improve a certain important performance of the system. However, we may not focus on the exergy destruction or the certain performance in many practical applications. We should pay enough attention to this point to avoid abusing the EGM.
In this paper, the role of the EGM in thermal optimization is discussed. As is well known, entropy generation can be used to measure the irreversibility of the thermal process. The view angle of irreversibility of entropy generation is analyzed. It is shown that entropy generation directly reflects the exergy destruction or the loss of ability to do work. In the system performance analyses, the EGM may not lead to the optimal value of the design objective because the objective may not always be consistent with the view angle of irreversibility of entropy generation.
In the heat transfer process in which heat is transferred only for heating or cooling objects, the inconsistence between the design objectives and the entropy generation rate is presented with some examples. In particular, the “entropy generation paradox” in heat exchanger analyses is discussed. We show that the concept of entropy generation is not a suitable parameter to evaluate the heat transfer performances of heat exchangers.
In the heat–work conversion system, the inconsistence between the design objectives and the EGM is also shown and discussed. As entropy generation may not directly describe the design objectives, but describes the exergy destruction, the applicability of the EGM is conditional.
In the thermal system, the decrease of irreversibility from the viewpoint of entropy generation may reduce the exergy destruction or improve a certain performance of the system that may not be the focus in many practical applications. This point should be considered to avoid abusing the EGM.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |