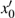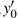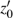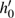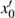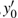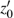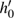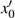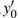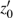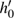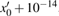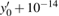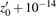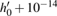Cite this Article
Luo Yu-Ling, Zhou Rong-Long, Liu Jun-Xiu, Qiu Sen-Hui, Cao Yi. A novel image encryption scheme based on Kepler’s third law and random Hadamard transform. Chinese Physics B, 2017, 26(12): 120504  
Permissions
A novel image encryption scheme based on Kepler’s third law and random Hadamard transform
Luo Yu-Ling1, Zhou Rong-Long1, Liu Jun-Xiu1, †, Qiu Sen-Hui1, 2, Cao Yi3
Guangxi Key Laboratory of Multi-Source Information Mining and Security, Faculty of Electronic Engineering, Guangxi Normal University, Guilin 541004, China
Guangxi Experiment Center of Information Science, Guilin 541004, China
Department of Business Transformation and Sustainable Enterprise, Surrey Business School, University of Surrey, Surrey, GU2 7XH, United Kingdom

 

† Corresponding author. E-mail: liujunxiu@mailbox.gxnu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61661008 and 61603104), the Natural Science Foundation of Guangxi Zhuang Autonomous Region, China (Grant Nos. 2015GXNSFBA139256 and 2016GXNSFCA380017), the Funding of Overseas 100 Talents Program of Guangxi Provincial Higher Education, China, the Research Project of Guangxi University of China (Grant No. KY2016YB059), the Guangxi Key Laboratory of Multi-source Information Mining & Security, China (Grant No. MIMS15-07), the Doctoral Research Foundation of Guangxi Normal University, the Guangxi Provincial Experiment Center of Information Science, and the Innovation Project of Guangxi Graduate Education (Grant No. YCSZ2017055).

Abstract

In this paper, a novel image encryption scheme based on Kepler’s third law and random Hadamard transform is proposed to ensure the security of a digital image. First, a set of Kepler periodic sequences is generated to permutate image data, which is characteristic of the plain-image and the Kepler’s third law. Then, a random Hadamard matrix is constructed by combining the standard Hadamard matrix with the hyper-Chen chaotic system, which is used to further scramble the image coefficients when the image is transformed through random Hadamard transform. In the end, the permuted image presents interweaving diffusion based on two special matrices, which are constructed by Kepler periodic sequence and chaos system. The experimental results and performance analysis show that the proposed encrypted scheme is highly sensitive to the plain-image and external keys, and has a high security and speed, which are very suitable for secure real-time communication of image data.

PACS: 05.45.Gg;05.45.Vx;05.45.-a
Keyword:Kepler’s third law;random Hadamard transform;interweaving diffusion;security
1. Introduction

The secure and real-time communication of image data is becoming more and more important, since the digital image plays a significant role in our life with the prevalence of the internet and information technology.[1–3] Due to a bulky data redundancy and high correlation between adjacent pixels, the traditional encrypted schemes are not suitable for the image encryption through internet.[4] Then the chaos-based image encryption methods have been utilized due to its superior characteristics,[5] including sensitivity to initial condition and controlling parameters, ergodicity, pseudo-randomness, and nonlinear unpredictability. The primary image encryption algorithms are based on some simple low-dimensional chaotic systems, and their security and plasticity are not good. Therefore, the experts proposed the high-dimensional hyper-chaotic systems by analyzing the nonlinear dynamic characteristics[6,7] to be used in the design of image encryption schemes.Since then, a variety of chaos-based image encryption algorithms have been proposed.[8–20]

Inspired by the architecture of permutation-diffusion which is first presented by Shannon,[21] most of the chaos-based image encryption schemes are based on not only this architecture, but also a combination with other theory, such as, compression sensing,[13,14] DNA sequences,[15] geometric transformation,[2,16] and physical phenomenon.[17–19] Specifically, Chai et al. proposed a visually secure image encryption scheme by using the zig–zag confusion and compression sensing,[13] which can achieve the image data security and image appearance security simultaneously to reduce the possible transmission bandwidth and storage space. Zhou et al. presented an efficient image compression-encryption scheme based on the hyper-chaotic system and two-dimensional (2D) compressive sensing.[14] A novel image encryption scheme based on deoxyribonucleic acid (DNA) sequence operations and chaotic system was proposed.[15] Wu et al.[16] proposed a new lossless encryption algorithm for color images based on a six-dimensional (6D) hyper-chaotic system and the 2D discrete wavelet transform (DWT) in both the frequency domain and the spatial domain. Wang et al.[17] proposed a new image encryption scheme, which used the simulated annealing algorithm to generate the random sequence for the confusion phase. The merit of this scheme is that the random sequence is generated excellently. Ye et al.[18] adopted self-cited pixel summation to produce the keystreams to be used in both permutation and diffusion process. And in Ref. [19] a novel image encryption algorithm based on three-dimensional (3D) Brownian motion and chaotic systems was presented to overcome the limitation of movement range of bits.

In spite of having such a superiority, few schemes have been used due to some drawbacks they have. For instance, a lookup table-based image encryption scheme[22] was analyzed to beable to be broken by chosen-plain-text attack and chosen-ciphertext attack[23] due to an algebraic weakness of the scheme. And a general attack scenario was given in order to conduct security analyses of chaos-based cryptosystems and the proposed general attack scenario was applied to recently proposed chaos-based image encryption scheme in Refs. [24] and [25]. A symmetrical image encryption algorithm based on skew tent map[26] was found to be vulnerable to differential attack.[27] An image encryption scheme based on DNA coding and information entropy[28] is found to have two vulnerabilities to make the encryption fail under chosen-plain-text attack; one is that entropy fails to protect permutation indexes under chosen-plain-text attack, and the other is the substitution of elements in the last column leak patterns of the encoding rule so that it permits recovering the encoding rule and covering matrix after breaking the permutation.[29]

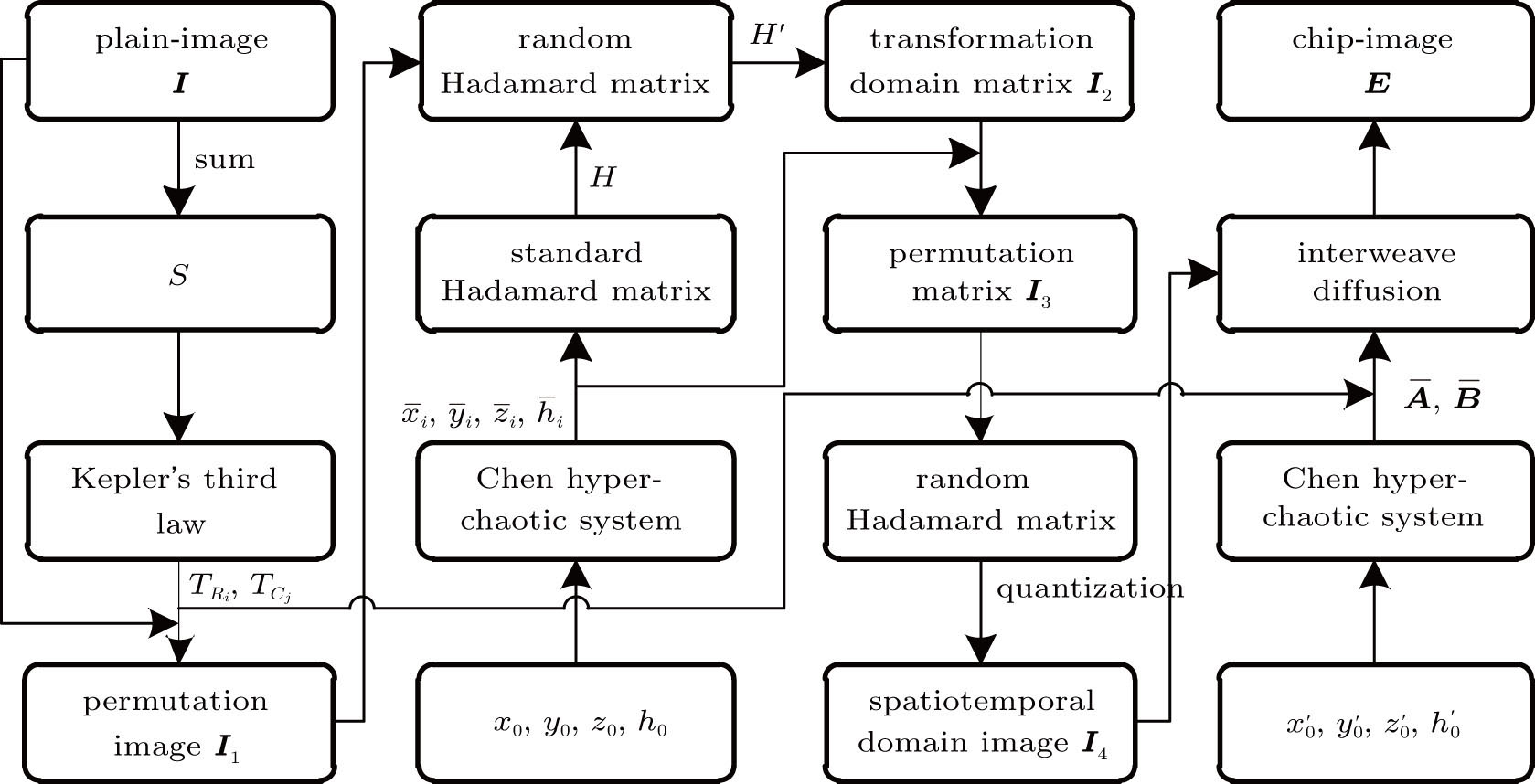
Inspired by the above cryptanalysis and improvement in chaos-based image encryption schemes,[22,24,26,28] a novel image encryption algorithm based on the Kepler’s third law and random Hadamard transform is proposed in the paper. First of all, two Kepler periodic sequences are generated in terms of the theory of Kepler’s third law, which is used to scramble the image. Then, a random Hadamard matrix is constructed by combining the standard Hadamard matrix with the chaos system, and it is utilized to transform image data to coefficients in Hadamard domain to be further permuted and we can obtain the permuted image by the inverse Hadamard transform. Furthermore, an interleaving diffusion based on two special matrices is adopted to increase the security of scheme. In the proposed encryption algorithm, both the permuted process and the diffusion process are closely related to the plain-text because of the rule of the Kepler’s third law. Specifically, the period of circle shifting in the permutation process and the diffusion sequences are determined by the coordination distribution of each pixel and the quality of plain-text, which greatly enhance the sensitivity of algorithm to plain-text and improve the ability to resist the differential attack and statistical security. Besides, the universal gravitational constant G of the Kepler’s third law can further increase the randomness of chaotic sequences to prevent violent attacks. In addition, the execution speed of image encryption can be improved by using the random Hadamard transform because it is very suitable for 2D data processing and can increase further the scrambling effect.

The rest of this paper is organized as follows. In Section 2 briefly introduced are the knowledge of Kepler’s third law Hadamard transform, and their preparation and link for the design of image encryption. In Section 3 the proposed encryption scheme is revealed and the experimental examples and results are given. In Section 4 the performances of the proposed scheme are analyzed and the results are compared. And finally, some conclusions are drawn deomthe present study.

2. Preliminaries
2.1. Hyper-Chen chaotic system

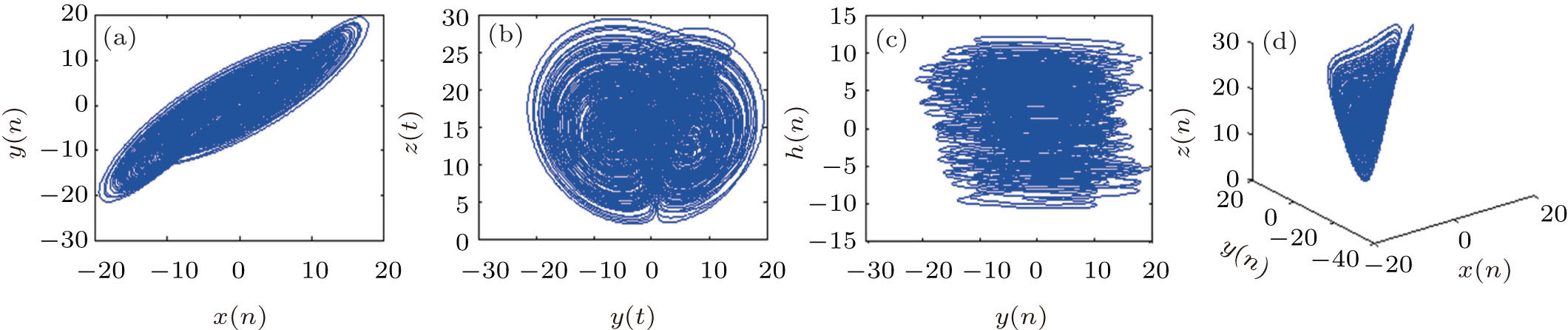
Compared with general chaos system, the hyper-chaotic system has many outstanding characteristics, e.g., many complex dynamical characteristics, good randomness and unpredictability, large key spaces, and various applications in today’s image encryption.[30–32] According to the further analysis of the Chen system,[33] a Chen-based hyper-chaotic system has been proposed and used in information security,[34,35] which is defined by

where x, y, z, and h are the state variables and a, b, c, d, and k are the controlling parameters of system. The dynamical orbit would be hyper-chaotic when a = 36, b = 3, c = 28, d = −16, and −0.7 < k < 0.7. Specifically, with k = 0.2 assumed,the Lyapunov exponents of system are 1.552, 0.023, 0, −12.573, respectively,[36] and the phase distribution of system is shown in Fig. 1.

Fig. 1. (color online) Attractors of the Chen hyper-chaotic system in (a) the x,y plane, (b) x,z plane, (c) y,h plane, and (d) in x,y,z space.
2.2. Kepler’s third law

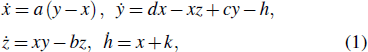
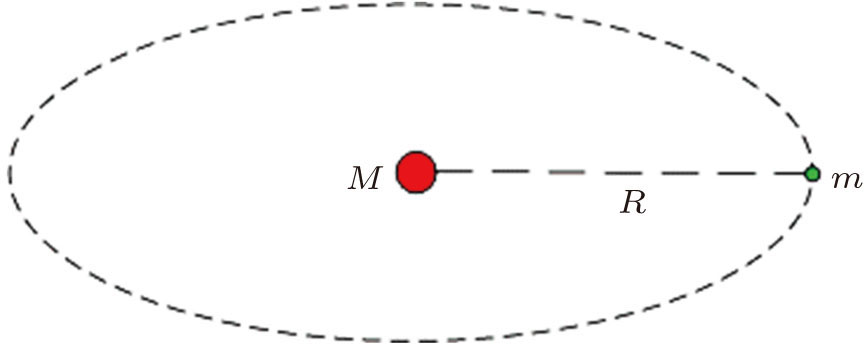
Kepler’s third law is well known in planetary motion of physics,[37] which reveals that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of its orbit. It can be described by

where K is a ratio, T is the period, and R is the semi-major axis of its orbit.

Now, we come to derive planetary motion for an elliptical orbit shown in Fig. 2, assuming mass m is orbiting mass M, with R being the radius of the orbit, according to Newtonian mechanics, Kepler’s third law can also be given by

where G is the gravitational constant (G ≈ 6.67 × 10−11 N·m2/kg2).

Fig. 2. (color online) Elliptical orbit of planetary motion.

Re-arranging Eqs. (2) and (3), the period of the orbit is obtainedby

2.3. Random Hadamard transform

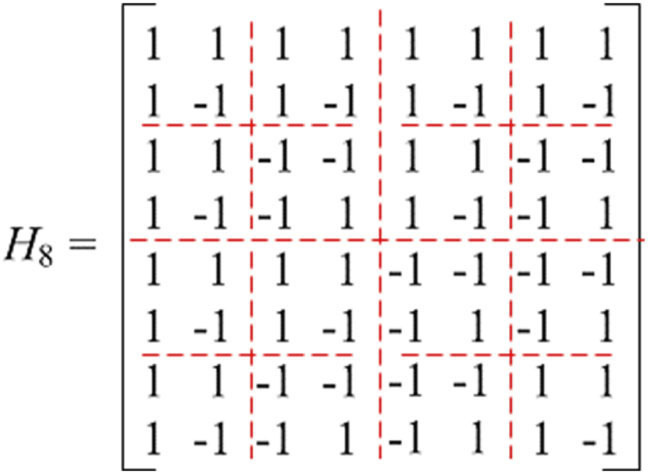
The Hadamard transform (HT) is an example of a generalized class of Fourier transforms, which can be applied to the fast discrete image transform. The Hadamard matrix is the kernel of the HT, and it is a square matrix composed of −1 and 1 as shown in Fig. 3 (an 8 × 8 standard Hadamard matrix). In accordance of definition of the HT, the n-th order Hadamard matrix should satisfy the following equation:

where In is the n × n identity matrix, and is the transpose of Hn. It can be seen that each row or each column of Hn is a orthogonal vectors over the field of real numbers and each length is . The forward transform of traditional HT can be defined by

where An and Bn are both an n × n square matrix, and the corresponding inverse transform is given by

Fig. 3. (color online) 8 × 8 standard Hadamard matrix.

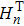
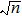
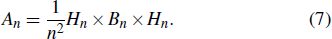
Because of the orthogonal property of Hadamard matrix, a kind of a random Hadamard matrix (RHM) can be constructed through changing the location of element in Hadamard matrix based on chaos theory, the detailed steps of which are as follows.

Step 1 Set a standard Hadamard matrix with a size of n × n, denoted as Hn.

Step 2 Generate four chaotic sequences by using the Chen hyper-chaotic system. Specifically, the initial conditions are set to be x0 y0, z0, and h0, and the iteration time is set to be 500+N. Then four chaotic sequences can be obtained and set to be xi, yi, zi, and hi (i = 501, 502, 503,..., 500+N).

Step 3 Quantization of the chaotic sequences by using the following equation:

where ⌊x⌋ returns the largest integer greater than or equal to x, and abs(·) returns a positive value.

Step 4 Exchange the locations of element in row and column of Hn to obtain a random Hadamard matrix , the specific rule is that if , the -th row of Hn is exchanged with the -th row of Hn. And this process will be completed until i = 500 + N. Then the column vectors are operated by a similar rule, that is, if , the -th column of Hn is exchanged with the -th column of Hn to obtain the novel Hadamard matrix until i = 500 + N. As for this novel Hadamard matrix , there will be the analogous transformation equation given by

2.4. Permutation technology based on Kepler’s third law and random Hadamard transform

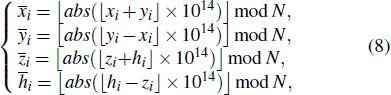
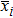
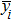
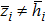
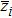
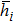
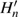
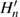
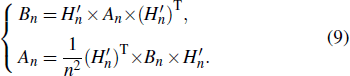
A good permutation technology can resist occlusion well, so it generally includes several features, that is: 1) the probability of changing the position of each pixel is basically the same; 2) the correlation between adjacent pixels should be seriously broken; 3) the distance between adjacent pixels of original should be become larger and larger. Considering these basic requirements, on the basis of the Kepler’s Third Law, the movement period of the barycenter of each row or column surrounding the barycenter of the whole image is first calculated, which is used as the parameter of cyclic shift cycle to scramble the plain image in the spatiotemporal domain. Specifically, the plain image is transformed by the RHT into another matrix, each row and each column of this matrix are scrambled based on the rule of cyclic shift cycle, and the scrambled image can be obtained through the Hadamard inverse transform in Eq. (9).

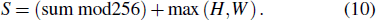
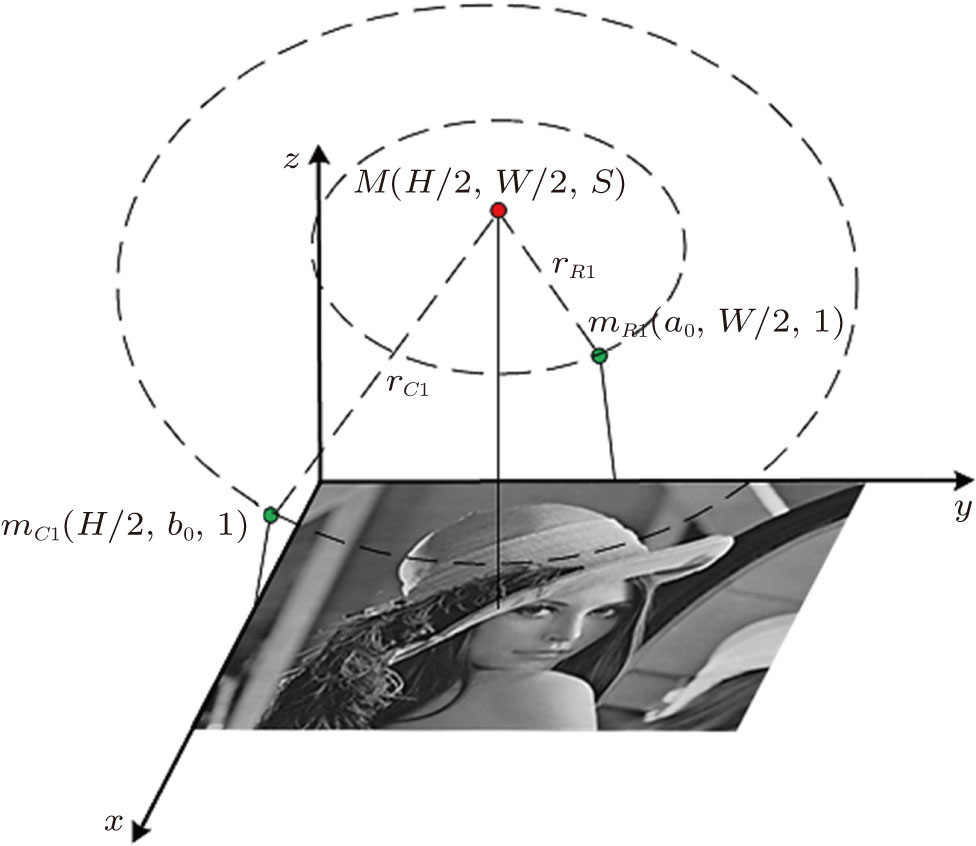Generally, the coordinates of each pixel and barycenter of image should be determined to compute the movement period. For example, a Lena image I witha size of H × W, is mapped to a three-dimensional Cartesian coordinate system as shown in Fig. 4, in which M is assumed to be the barycenter of image I, and mR1 and mC1 are assumed to be the barycenter of the first row and the first column, respectively. If the sum of all gray values of image I is denoted as sum, the coordination of barycenter of image I can be determined to be M(H/2, W/2,S), where the axis S is computed by an easy quantification operation of

Fig. 4. (color online) Determination of coordination of barycenter of image based on Kepler’s third law.

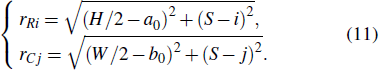
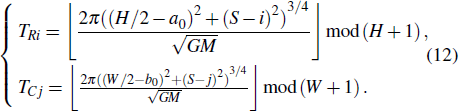
As shown in Fig. 4, the coordinate in y axis for each row is defined as W/2, and z denotes the z-th row or z-th column, for example, the coordination of barycenter of the first row is expressed as mR1(a0,W/2,1). Therefore, the coordinations of barycenter of each row and column can be defined as mRi(a0,W/2,i) and mCj(H/2,b0,j), where two import constants a0 and B0(0 < a0 < H,a0 ≠ H/2;0 < b0 < W, b0 ≠ W/2) are used to distinguish the barycenter between rows and columns, i = 1,2,3,...,H; j = 1,2,3,...,W. Then the distance between the barycenter of each row (or barycenter of each column) and the barycenter of the whole image can be calculated from

Combining Eq. (11) with Eq. (4), the cyclic shift period of each row or each column can be expressed as

As mentioned above, the parameters TRi and TCj are used as the controlling variables to adjust the cyclic shift operation, and the specific method is given below.

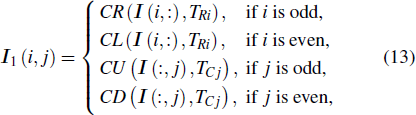
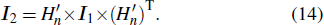
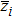
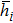
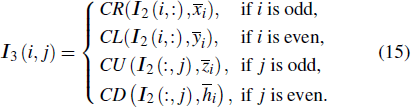
where I1 is the scrambled image, CRCL, CU, and CD denote the four cyclic shifts for different rows and columns. Then the scrambled image I1 is transformed into another matrix I2 by the RHT of

Besides, the integer sequences , , , and are further used to adjust the times of circular shift for different rows and columns of matrix I2 to obtain matrix I3, and the operation is given by

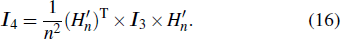
Finally, the permuted image I4 in the spatiotemporal domain can be taken through the inverse RHT of

2.5. Interweaving diffusion technology

As mentioned above, the parameters TRi and TCj are tightly related to the plain image. Therefore, the encryption scheme would be better if these two parameters are applied to the process of diffusion, which is described as follows.

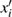
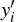
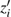
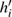
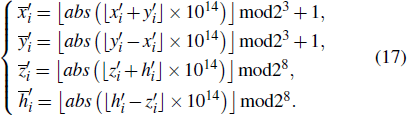
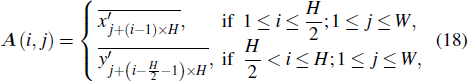
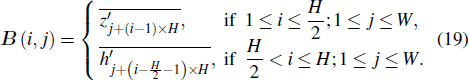
Firstly, re-iterate the hyper-Chen system (500 + (H × W)/2) times, and extract the back (H × W)/2 data to obtain novel four sequences, i.e., , , , and . Then the sequences are quantified into

Then, two pre-encrypted matrices A and B are constructed by

and

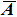
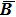
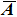
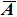
Moreover, the matrices A and B are rearranged in terms of Eq. (13) to obtain two novel matrices and , and is used to control the right loop shift of each pixel of the permuted image I4 in the bit-plane by I4(i,j) = BR(I4(i,j), (i,j)), i.e., assuming c = BR(a, b) and a = 125, b = 5, after the right loop shift by 5, the a becomes 235 and this value is assigned to c, i.e., c = 235.

In order to improve the diffusion performance, on the basis of the operation

the image I4 is first diffused with , and further encrypted to obtain the final cipher-image by

3. Encryption example and experimental results
3.1. Encryption process for several images

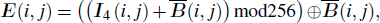
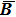
As described above, the whole encrypted scheme contains the permutation and diffusion, which cross each other as shown in Fig. 5. Taking several images for example, the detailed encrypted scheme is shown by the several steps below.

Fig. 5. Diagram of the encryption process.

Step 1 Calculate the summation of grey values of any image I to obtain the axis S by using Eq. (10).

Step 2 Compute the controlling parameters TRi and TCj by using Eqs. (11) and (12).

Step 3 Cycle-shift the rows and columns of image I to obtain I1 in terms of Eq. (13).

Step 4 Generate the chaotic sequences , , , by using Eq. (8).

Step 5 Choose a standard Hadamard matrix, and construct the corresponding random Hadamard matrix in terms of , , , according to Step 4 in Subsection 2.3.

Step 6 Transform matrix I1 into matrix I4 according to Eqs. (14)–(16), and all values of I4 are mapped into an integer range from 0 to 255.

Step 7 Construct matrices A and B by using Eqs. (18) and (19) and rearrange them to obtain matrices and .

Step 8 Diffuse the permuted image I4 to obtain the final Chip-image E.

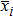
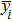
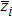
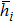
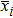
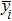
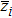
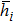
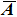
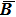
The decrypted process is the corresponding inverse process shown in Fig. 6.

Fig. 6. Diagram of decryption process.
3.2. Experimental results

In the experiments, multiple standard grey images with a size of 512 × 512 are tested. All the simulations are done under the MATLAB R2014a platform on a Windows 7 operating system with Intel(R) Xeon(R)E3-1246 CPU 3.5 GHz (E6500) processor with 8 GB of random-access memory. Two sets of initial data for the hyper-chaotic Chen system are randomly chosen, which are {x0 = 0.1314, y0 = 0.5214, z0 = 0.3689, h0 = 0.8419 and 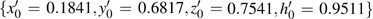. And the controlling parameters are a = 36, b = 3, c = 28, d = −16, k = 0.7, and distinguishing parameters are a0 = 20 and b0 = 30. The experimental results are shown in Fig. 7, and figures 7(a)–7(e) are the five plain-images, figures 7(f)–7(j) are corresponding cipher-images, and figures 7(k)–7(o) are the decrypted images with the correct keys and parameters.

Fig. 7. (color online) Results of encryption and decryption showing ((a)–(e)) original images of Lena, Baboon, Peppers, Plane, Milkdrop, ((f)–(j)) the corresponding cipher-images of panels (a)–(e) and ((k)–(o)) the decrypted images with correct keys, respectively.
4. Performance analysis and discussion
4.1. Key space analysis

As a good image encryption system, the key space must be large enough to resist the adversaries guessing the key using a brute-force attack.[38] For the proposed encrypted scheme, the key consists of two parts: 1) two sets of initial values of the hyper-chaotic Chen system (x0, y0, z0, h0) and 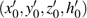and 2) two distinguishing parameters a0, b0 (0 < a0 < H, a0 ≠ H/2;0 < b0 < W,b0 ≠ W/2). If computational precision is set to be 10−15, the size of key space is about 10150, which is much larger than basic requirement 2100.[39] Thus it can be seen that the key space of the proposed algorithm is large enough to withstand brute-force attacks.

4.2. Differential attack analysis

Differential attack (DA) is an important criterion to measure the merits of the encryption algorithm, which requires that a slight change in the plain-image can cause a significant difference in the cipher-image. Two metrics are used to test DA: the number of pixel’s change rate (NPCR) and the unified averaged changing intensity (UACI), which can be calculated from

and

where C1 and C2 are the two cipher-images whose corresponding plain-images have only one-bit difference, and D(i, j) is

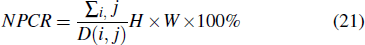
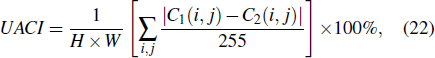
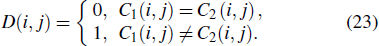
The expected values of the NPCR and UACI are 99.6094% and 33.4635%, respectively.[18] We randomly choose five different locations of the five different plain-images for experiment and test, and the corresponding results of NPCR and UACI are listed in Table 1. The average values of the NPCR and UACI are 99.6394% and 33.5489%, respectively, which are bothclose to the expected values. Therefore, it can be seen that the proposed scheme can resist the DA.

Table 1.

NPCR and UACI for different plain images.

.
4.3. Key sensitivity analysis

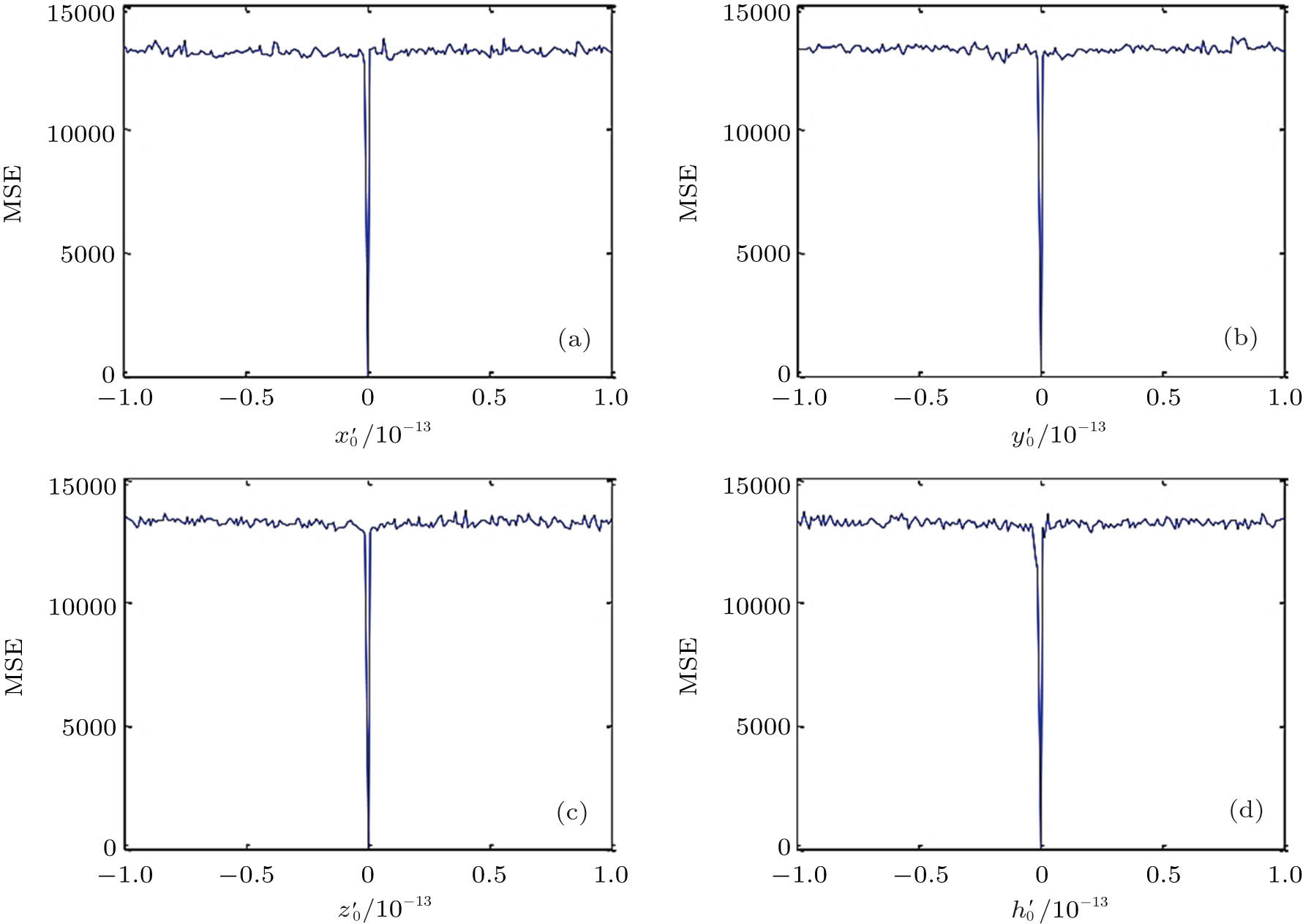
According to the Kerckhoff’s principle,[40] a high sensitivity to the key is critical for a secure encrypted scheme. Taking the Lena image shown in Fig. 7(a) for example, the original encrypted image is shown in Fig. 7(f). When the keys of initial values x0, y0, z0, h0 are changed byone bit (e.g., 10−14, respectively, the four new encrypted images are obtained shown in Figs. 8(a)–8(d). Comparing them with the original cipher-image, the four differential charts are shown in Figs. 8(e)–8(h). And figures 8(i)–8(l) are the corresponding histograms of Figs. 8(e)–8(h), which show that there are huge differences between the original cipher-image Fig. 7(f) and Figs. 8(e)–8(h). Then, the permutation sequences TRi and TCj are changed only a little, and they are used to permute toobtain two novel permutation images I11 and I12. By comparing I11 and I12 and the original permutation image I1, the corresponding NPCR values are calculated from Eq. (21), and the results are 97.9637% and 98.8960%, respectively. It illustrates that permutation image I1 is strongly sensitive to TRi and TCj.

Fig. 8. (color online) Cipher-images within correct initial keys and the differences between them and the original encrypted images: ((a)–(d)) four new encrypted images with the keys of x0 + 10−14, y0 + 10−14, z0 + 10−14, h0 + 10−14; ((e)–(h)) differences between the incorrect encrypted images and the original image, and ((i)–(l)) their corresponding histograms.

Besides, the mean square error (MSE) between original image and decrypted image can be used to evaluate the key-sensitivity of encryption algorithm.[41] The MSE is calculated from

where C and P are the decrypted image and the plain-image respectively. The H × W is the image size. Similarly, the original encrypted image shown in Fig. 7(f) is decrypted by using the changed initial values , which are deviated only a little from the correct keys x0, y0, z0, h0. Figure 9 shows the MSE curves for initial keys, respectively. As shown in Fig. 9, it can be seen that the MSE is very large even with a little deviation from the correct keys. Thus, the proposed scheme is highly sensitive to the initial keys to make the attacker difficult to exhaust the correct keys.

Fig. 9. (color online) MSE curves for the incorrect initial keys: (a) ; (b) ; (c) ; (d) .
4.4. Information entropy

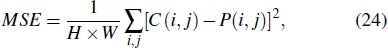
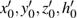
Information entropy is often used to measure the confusion degree of information sources, and prevent the attacker from utilizing its image characteristics to crack, which is given by

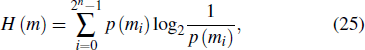
where p(mi) represents the probability of symbol mi, n is the bit number of each symbol mi.[42] From Eq. (25), the ideal H(m) should be 8 for the good encrypted image with 256 grey-levels. The test results of five encrypted images are shown in Table 2, which shows that the entropy of each encrypted image is close to 8, in the other words, the encryption scheme can effectively hide the image information.

Table 2.

Results of information entropy.

.
4.5. Statistical Analysis
4.5.1. Histogram analysis

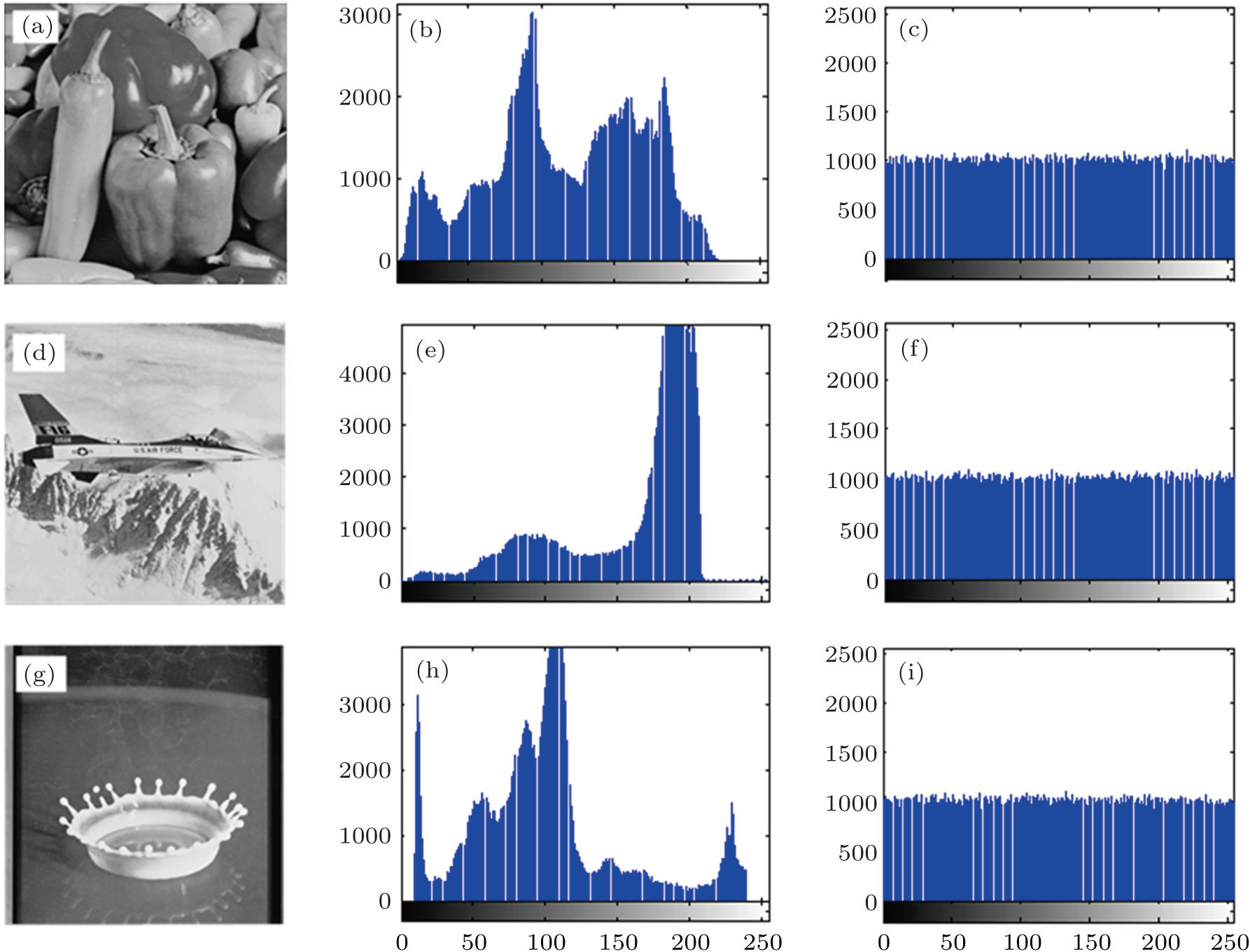
A good encryption algorithm must make the histogram of encrypted image uniform to be robust against the statistical analysis. Figure 10 shows the histograms of three plain-images (Peppers, Plane, and Milkdrop) and their corresponding cipher-images, indicating that the histogram distribution of the original image is not smooth, but the encrypted image is uniform.

Fig. 10. (color online) Histograms of the different plain- and cipher-images: ((a), (d), and (g)) plain-images “Peppers”, “Plane”, and “Milkdrop”; ((b), (e), and (h)) histograms of plain-images; ((c), (f), and (j)) histograms of their corresponding cipher-images.

In addition, the variance of the histogram can be used to evaluate the uniformity of the encrypted image.[43] The smaller the variance of the histogram, the better the uniformity of the encrypted image is. The variance of the histogram can be calculated from

where Z is a vector of the histogram values (e.g., Z = Z(1), Z(2),…, Z(256)}), and Z1(i) and Z2(j) are the numbers of pixels of which the gray values are equal to i and j, respectively. Therefore, the variances of histograms of two ciphered images by Eq. (26) from the same plain-text with different secret keys are calculated, and at each time only a parameter of the secret keys is changed. The results of five images (in Figs. 7(a)–7(e)) are listed in Table 3. From Table 3, it can be seen that the variance values of the histogram are about 1000, which indicates that the average fluctuation of number of pixels in each gray value is about 32 pixels. Comparing with the average fluctuation 74 of number of pixels in Zhu’s algorithm,[44] the proposed algorithm has good uniformity and statistical properties.

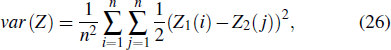
Table 3.

Comparison among variancesof histograms of all secret keys in the proposed algorithm.

.

Besides, the percentage of variance differences can be also used to measure the uniformity of each parameter of the secret keys, which is calculated from

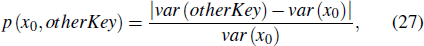
where p( x0, otherKey) is the percentage of variance difference between the secret key x0 and otherKey that only one parameter is changed, var( x0) and var( otherKey) represent the histogram variances of the secret key x0 and otherKey. The experimental results of five images fordifferent keys are listed in Table 4, showing that the average percentage of variance differences of each secret key is less than 7%, i.e., the change of each secret key will lead to the variance fluctuation with about 7%. In addition, the corresponding percentages of variance differences of different images are changed obviously as shown in Table 4, which indicates that the histogram distribution is strictly related to the plain-text.

Table 4.

Comparison among percentages of variances difference of histograms of all secret keys in the proposed algorithm.

.
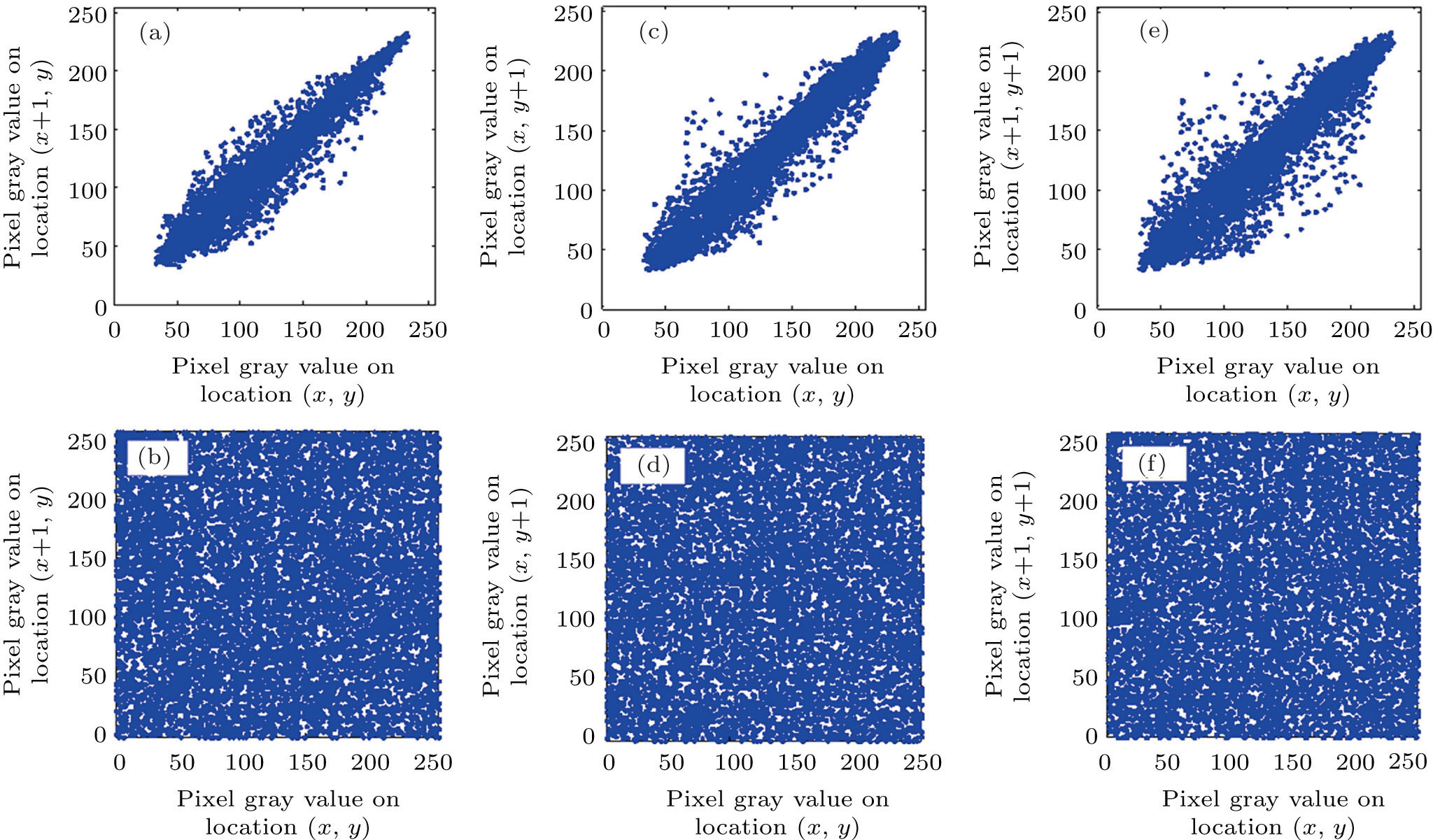
4.5.2. Correlation-coefficient analysis

Any natural image contains a large amount of redundant information about a great correlation between two adjacent pixels, which can be considered as an important information about the crack made by attacker. Therefore, the test of correlation-coefficient is also a vital factor to measure the performance of the encrypted scheme. The as 104 adjacent pixels are randomly chosen in the horizontal, vertical and diagonal directions of the plain-image (Fig. 7(a) Lena) and cipher-image (Fig. 7(f)) respectively, and then are plotted in the plane shown in Fig. 11. It can be seen that there is a high correlation of the plain-image, but the correlation of the cipher-image is greatly eliminated.

Fig. 11. (color online) Correlation distributions of the original image (Lena) and the corresponding cipher-image in the ((a) and (b)) horizontal direction, ((c) and (d)) vertical direction, and ((e) and (f)) diagonal direction.

Moreover, the specific correlation coefficient rxy between adjacent pixels can be calculated from

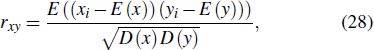
where and x and y are grey values of two adjacent pixels, and N is the total number of pixels selected from the image. Table 5 shows the average values of correlation coefficient of the plain-image and the cipher-image in three directions. We can clearly find that the correlation coefficients of adjacent pixels of the original image are close to 1, but the correlation coefficients of adjacent pixels of cipher-image almost equal 0, which further illustrates that the proposed encrypted scheme has a strong resistance to statistical attack.

Table 5.

Correlation coefficients of plain- and cipher-images.

.
4.6. Occlusion and noise attack analysis

Occlusion attack and noise interference are inevitable in the information transmission due to network failure or network congestion, thus they are also two important test parameters to measure the performance of encrypted scheme, i.e., a good encryption algorithm must have a strong robustness against the occlusion attack and noise attack. Figure 12 shows the test results of occlusion attack, in which figures 12(a)–12(d) are the cipher-images of the plain-image Lena (shown in Fig. 7(f)) with 12.5%, 25%, 50%, and 75% occlusion respectively, and figures 12(e)–12(h) are their corresponding decrypted images, respectively. From the results, the quality of the decrypted image is still acceptable and good even if the cipher-image has a 75% loss, which illustrates that the original image information is fully diffused in the encryption process.

Fig. 12. Occlusion attack analysis: (a) cipher-image with 12.5% occlusion, (b) cipher-image with 25% occlusion, (c) cipher-image with 50% occlusion, (d) cipher-image with 75% occlusion, ((e)–(h)) decrypted images of ((a)–(d)) images.

On the other hand, the Salt and pepper noise and Gaussian noise are common noises to be experimented to test the noise attack, and the results are shown in Figs. 13 and 14, respectively. The results demonstrate that the proposed scheme has a strong robustness against the external interference, such as occlusion attack and noise attack.

Fig. 13. (color online) Salt and pepper noise attack analysis, showing ((a)–(c)) cipher-images with noise density = 5% (a), 10% (b), and 20% (c), and ((d)–(f)) the corresponding decrypted images.
Fig. 14. Gaussian noise attack analysis, showing ((a)–(c)) cipher-images with different levels of (a) noise mean = 0 and variance = 0.01, (b) mean = 0 and variance = 0.03, and (c) mean = 0 and variance = 0.05; ((d)–(f)) the corresponding decrypted images.
4.7. Classical types of attacks

Ciphertext only, known-plain-text attack chosen-plain-text attack, and ciphertext attack are four most powerful classical attacks, and the chosen-plain-text attack is the most powerful attack.[45] Therefore, if the algorithm can resist chosen-plain-text attack, it can resist other three types of attacks to some extent. As for the proposed encryption scheme, the controlling parameters TRi and TCj are closely related to the plain-image information S, thus even if there is only one bit of change happening in the plain-image, TRi and TCj would be completely different. 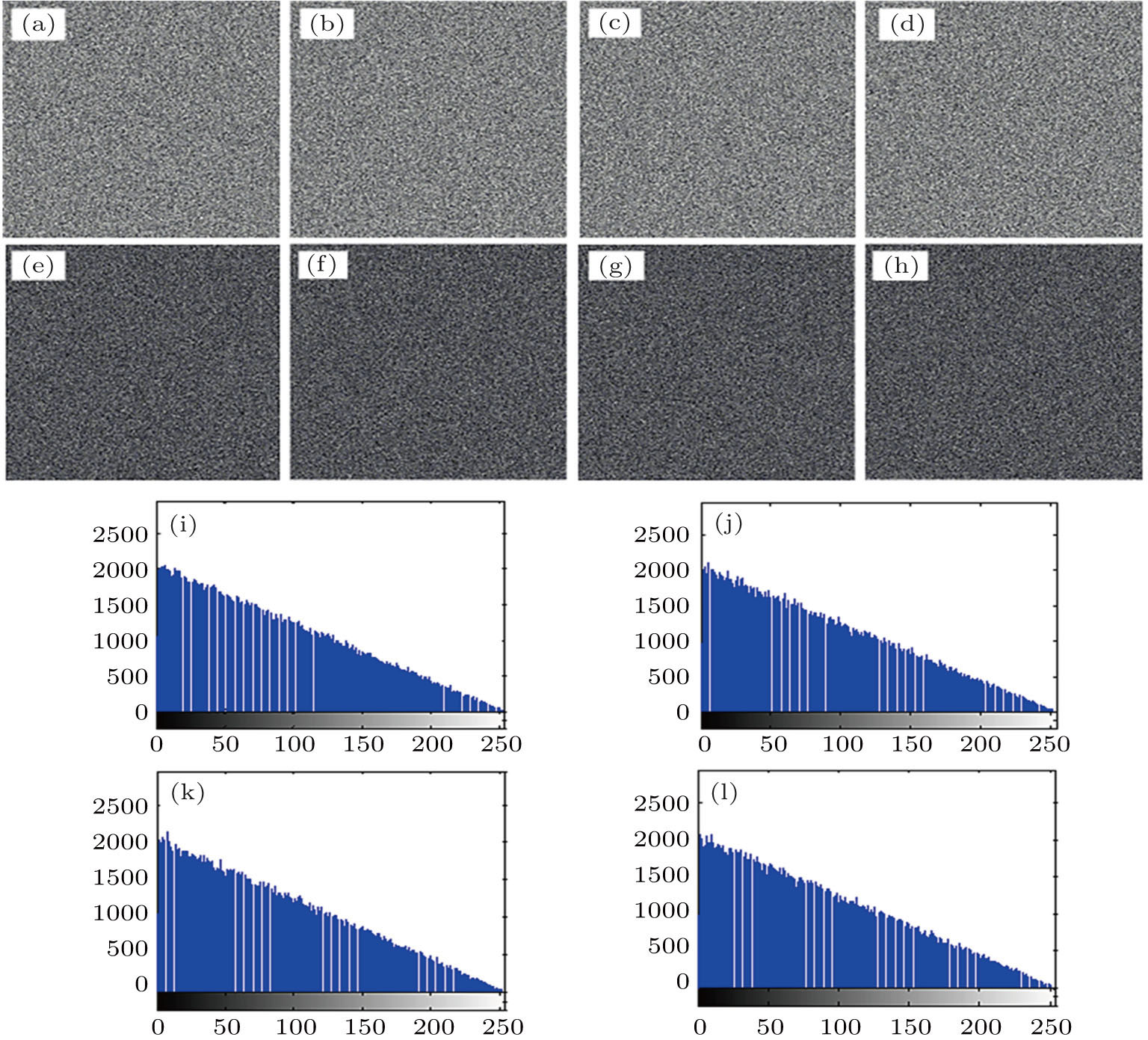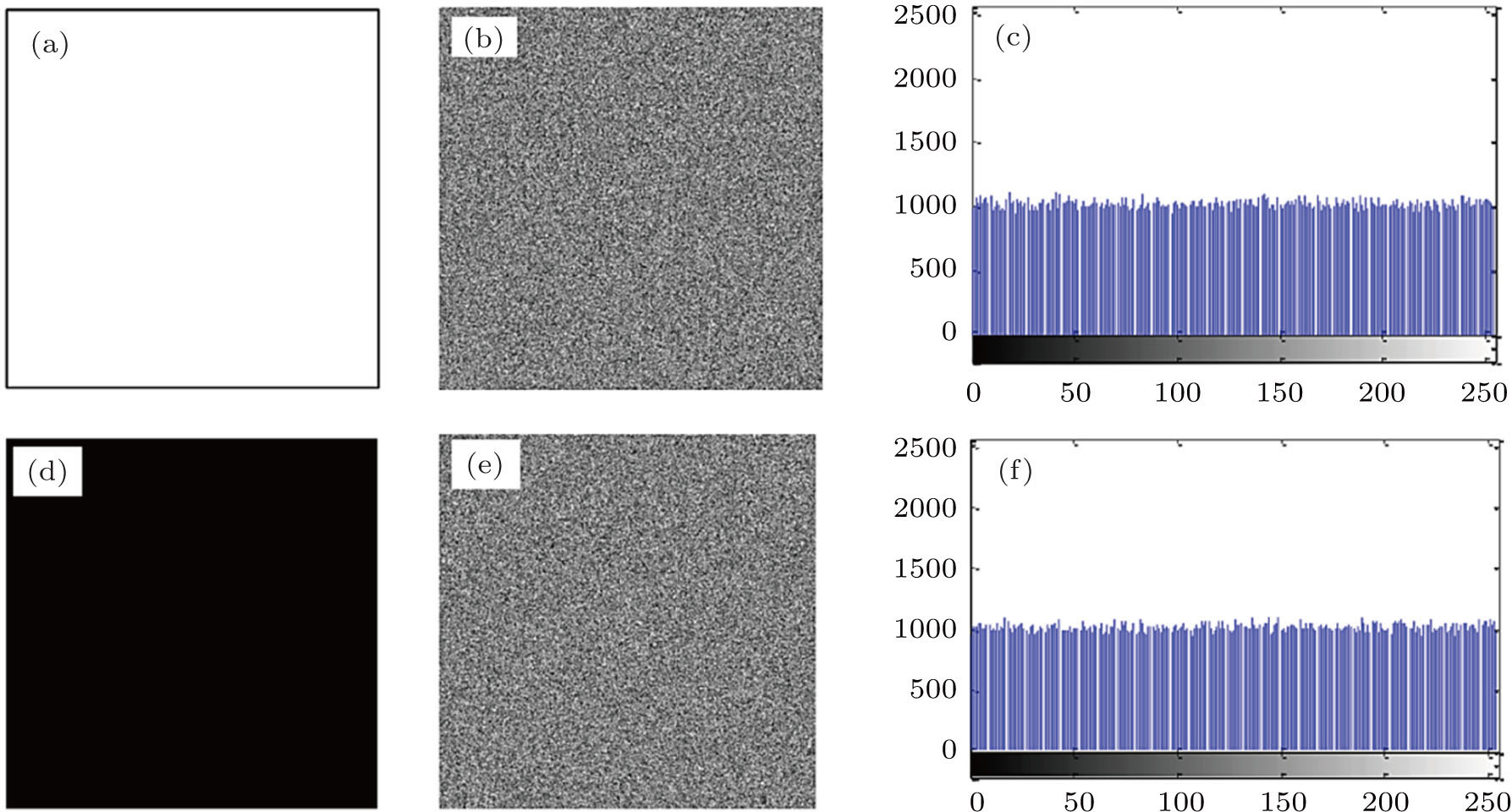Moreover, the diffusion matrices and are also strictly related to the plain-image information, and the diffusion technology is interweaving, which makes the scheme invulnerable to the known-plain-text/ciphertext attack to some extent.

Specifically, some special images are chosen to test the chosen plain-text attack, such as all-white image (Fig. 15(a)) and all-black image (Fig. 15(d)). The result is shown in Fig. 15, which indicates that the cryptosystem is suitable for these special images and the results are good to resist against chosen-plain-text attack.

Fig. 15. (color online) Chosen plain-image test for white and black images, showing (a) all white image, (b) cipher image of panel (a), (c) the histogram of panel (b), (d) all black image, (e) cipher image of panel (d), (f) the histogram of panel (e).

Besides, in order to test the ability of the proposed algorithm to resist the Ciphertext only attack, all the keys will be changed with 10−14 to decrypt the original encrypted image (see Fig. 7(f)) respectively. The decrypted images are shown in Fig. 16, which are totally different from the original image (see Fig. 7(a)). Therefore, it can be seen that the ciphertext cannot be effectively decrypted without the correct keys, on the contrary, it indicates that the proposed algorithm can effectively prevent the Ciphertext only attack.

Fig. 16. (color online) Wrong decrypted image for Lena with (a) x0 + 10−14, (b) y0 + 10−14, (c) z0 + 10−14, (d) h0 + 10−14, (e) , (f) , (g) , (h) , (i) a0 + 10−14, and (j) b0 + 10−14.
4.8. Speed analysis and comparisons

An effective encrypted time can ensure the real-time communication of information, and thus except for a high secure scheme, there needs an efficient execution speed as well. In this paper, the encryption scheme includes four processes: pre-permutation in spatiotemporal domain, permutation in Hadamard domain, encrypted matrix construction, and interleaving diffusion. Taking a standard image Lena 512 × 512 (263 kB) for example, the specific time distribution is shown in Fig. 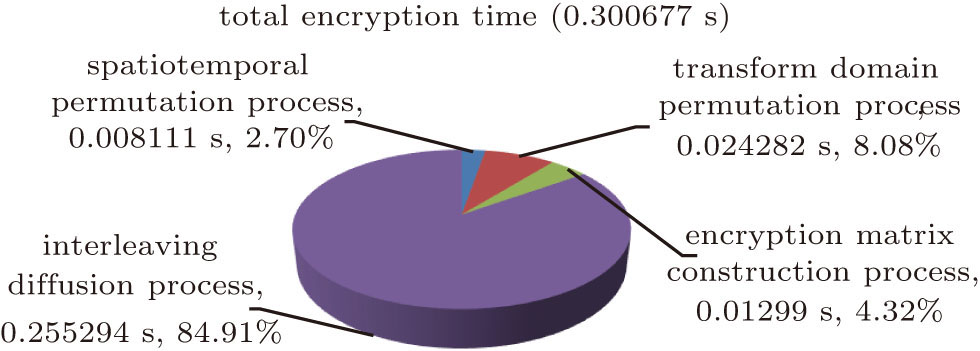17, which reveals that the interleaving diffusion process takes up the most of time in the whole encrypted process. Table 6 shows the relationship between the encrypted time and the size of the plain-image.

Fig. 17. (color online) Average encrypted time and percentage of each component of the proposed algorithm for Lena with a size of 512 × 512.
Table 6.

Relationship between encrypted time and the size of plain-image (in unit: s).

.

From Fig. 17, it can be seen that the execution time of permutation process is shortest because the random Hadamard transform is suitable for 2D data processing. For example, if the standard image Lena 512×512 is permutated by the random Hadamard transform method, the experimental time is 0.0223 s and the NPCR value is 99.5818%. However, the permutation times of two conventional scrambling methods (i.e., Cat map-based permutation[4] and Bit-level-based permutation[46]) are 0.2731 s and 0.6527 s, respectively, and the corresponding NPCR values are 98.0457% and 99.2715%. Therefore, the random Hadamard transform can not only improve the speed of encryption, but also increase the scrambling effect

Besides, in order to compare with other relavent encrypted schemes, the proposed encryption algorithm is executed 100 times to compute the average encrypted speed and other performances. The results are given in Tables 7 and 8, which illustrate that the proposed encrypted scheme has a good execution speed and secure performance and is suitable for the fast and secure image transmission Specifically, the execution speed is better than others in the literature except Ref. [49]. In Ref. [49], a low chaotic system is used to generate the sequence to scramble the pixel position, but it is only for once, thus it has a relatively high encryption speed.

Table 7.

Speed comparison of several cryptosystems (unit: Mb/s).

.
Table 8.

Performance comparison of several cryptosystems.

.
5. Conclusions

A novel hyper-chaos-based image encryption scheme is proposed in this study, which is based on the theory of Kepler’s third law and random Hadamard transform. And the classical permutation-diffusion encryption mechanism is adopted. In the permutation process, two Kepler periodic sequences are first generated in accordance of the image application of the Kepler’s third law, which is used to scramble the image. And the random Hadamard matrix based on chaos map is constructed to further permute the coefficients in the Hadamard domain, and then the permuted image can be obtained through the inverse Hadamard transform. In the diffusion process, two special matrices are constructed to complete the interleaving diffusion of each pixel. In order to improve the algorithm sensitivity to the plain image and the ability to resist the known-plain-text and chosen-plain-text attacks, the two Kepler periodic sequences used both in permutation process and in diffusion process and the two diffusion matrices are strong related to plain-image data. Several experimental and performance analyses, including key space analysis key sensitivity analysis differential analysis information entropy the histogram analysis correlation-coefficient analysis occlusion and noise attack analysis known-plain-text and chosen-plain-text attacks speed analysis and comparison show that the proposed algorithm is high sensitivity to original image, and has a good security and speed, which are suitable for image secure communication.In the future work, the capabilities of parallel implementation for color image encryption scheme will be considered and designed to make it optimal and universal in the application of image data field.

Reference
[1] Luo Y Du M 2013 Chin. Phys. 22 080503
[2] Luo Y Du M Liu J 2015 Commun. Nonlinear Sci. Numer. Simul. 20 447
[3] Hu T Liu Y Gong L H Ouyang C J 2017 Nonlinear Dyn. 87 51
[4] El Assad S Farajallah M 2016 Image Commun. 41 144
[5] Chai X Yang K Gan Z 2017 Tools Appl. 76 9907
[6] Chua L O 1971 Circuit Theory 18 507
[7] Chen G Dong X 1993 Int. J. Bifur. Chaos 3 1363
[8] Matthews R 1989 Cryptologia 13 29
[9] Lang J 2015 Opt. Commun. 338 181
[10] Chen J Zhu Z Fu C Yu H Zhang L 2015 Commun. Nonlinear Sci. Numer. Simul. 20 846
[11] Kalpana J Murali P 2015 Optik. 126 5703
[12] Wang X Xu D 2015 Nonlinear Dyn. 79 2449
[13] Chai X Gan Z Chen Y Zhang Y 2017 Signal Processing 134 35
[14] Zhou N Pan S Cheng S Zhou Z 2016 Opt. Laser Technol. 82 121
[15] Wang X Zhang Y Bao X 2015 Opt. Lasers Eng. 73 53
[16] Wu X Wang D Kurths J Kan H 2016 Inf. Sci. 349 137
[17] Wang X Liu C Xu D Liu C 2016 Nonlinear Dyn. 84 1417
[18] Ye G D Huang X L Zhang L Y Wang Z X 2017 Chin. Phys. 26 10501
[19] Chai X Gan Z Yuan K Lu Y Chen Y 2017 Chin. Phys. 26 020504
[20] Wang X Yang L Liu R 2010 Nonlinear Dyn. 62 615
[21] Shannon C E 1949 Bell Syst. Technol. J. 28 656
[22] Chen J Zhu Z Fu C Zhang L Zhang Y 2015 Nonlinear Dyn. 81 1151
[23] Hu G Xiao D Wang Y Li X 2017 Nonlinear Dyn. 88 1305
[24] Wang X Zhao J Liu H 2012 Opt. Commun. 285 562
[25] Özkaynak F Özer A B 2016 Opt. - Int. J. Light Electron Opt. 127 5190
[26] Zhou G Zhang D Liu Y Yuan Y Liu Q 2015 Neurocomputing 169 150
[27] Chen L Ma B Zhao X Wang S 2017 Nonlinear Dyn. 87 1797
[28] Zhen P Zhao G Min L Jin X 2016 Multimed. Tools Appl. 75 6303
[29] Su X Li W Hu H 2017 Multimed. Tools Appl. 76 14021
[30] Yaghouti Niyat A Moattar M H Niazi Torshiz M 2017 Opt. Lasers Eng. 90 225
[31] Liu Y Tong X Ma J 2016 Multimed. Tools Appl. 75 7739
[32] Tong X Zhang M Wang Z Ma J 2016 Nonlinear Dyn. 84 2333
[33] Zhou T Tang Y 2003 Int. J. Bifur. Chaos 13 2561
[34] Tan R Lei T Zhao Q Gong L Zhou Z 2016 Int. J. Theor. Phys. 55 5368
[35] Özkaynak F Yavuz S 2014 Nonlinear Dyn. 78 1311
[36] Gao T Chen Z Yuan Z Chen G 2006 Int. J. Mod. Phys. 17 471
[37] Dmitrašinović V Šuvakov M 2015 Phys. Lett. 379 1939
[38] Luo Y Cao L Qiu S Lin H Harkin J Liu J 2016 Nonlinear Dyn. 83 2293
[39] Dong C 2014 Signal Process. Image Commun. 29 628
[40] Pisarchik A N Flores-Carmona N J Carpio-Valadez M 2006 Chaos. 16 033118
[41] Zhang Y Xu B Zhou N 2017 Opt. Commun. 392 223
[42] Mirzaei O Yaghoobi M Irani H 2012 Nonlinear Dyn. 67 557
[43] Zhang Y Wang X 2014 Inf. Sci. 273 329
[44] Zhu Z Zhang W Wong K Yu H 2011 Inf. Sci. 181 1171
[45] Wang X Teng L Qin X 2012 Signal Processing 92 1101
[46] Liu H Wang X 2011 Opt. Commun. 284 3895
[47] Zhang X Fan X Wang J Zhao Z 2016 Tools Appl. 75 1745
[48] Li C Luo G Qin K Li C 2017 Nonlinear Dyn. 87 127
[49] Liu H Wang X 2010 Comput. Math. with Appl. 59 3320
[50] Liu H Wang X Kadir A 2012 Appl. Soft Comput. J. 12 1457
[51] Wang X Liu L Zhang Y 2015 Opt. Lasers Eng. 26 10
[52] Wang X Gu S Zhang Y 2015 Opt. Lasers Eng. 68 126
[53] Zhang Y Wang X 2015 Appl. Soft Comput. J. 26 10
[54] Wang X Luan D 2013 Nonlinear Sci. Numer. Simul. 18 3075