Based on the laws of quantum physics, quantum key distribution (QKD)^[1] allows two distant legitimate parties (typically called Alice and Bob) to share unconditionally secure keys, in the presence of the eavesdropper (Eve).^[2] Since the first Bennett–Brassard-1984 (BB84) QKD protocol was proposed,^[1] many successful QKD works have been achieved during the past decades.^[3–15] In most of these experiments, a feedback setup is needed to align the reference frames between Alice and Bob, which will undoubtedly increase the complexity and time cost of QKD systems. Otherwise, the high quantum bit error rate (QBER) will prevent the generation of net secret keys.

Fortunately, reference-frame-independent QKD (RFI QKD) was proposed by Laing et al.^[16] to avoid the active alignment of reference frames, which can obviously increase the whole communication efficiency between Alice and Bob. After that, a series of theoretical^[17–19] and experimental^[20–23] works on RFI QKD have been reported. However, none of them considered the practical scenarios including both source errors and statistical fluctuations.

In this paper, we investigate the performance of decoy-state RFI QKD in practical scenarios with two kinds of light sources, the heralded single photon source (HSPS) and the weak coherent source (WCS). The widely used vacuum + weak decoy-state method^[24–28] is adopted to combat the photon-number-splitting (PNS) attack^[29,30] caused by the multi-photons in the practical sources. Moreover, clear comparison results of decoy-state RFI QKD with WCS and HSPS are given, and simulation results show that the decoy-state RFI QKD even with both source errors and statistical fluctuations is very practical and robust.

RFI QKD employs three mutually unbiased bases (Z, X, and Y) to encode the information,^[16] which is very similar to the six-state protocol.^[31] During the quantum communication phase, Alice randomly prepares quantum states with her local bases X_A, Y_A, and Z_A, and sends them to Bob. Bob randomly measures the received states with his local bases X_B, Y_B, and Z_B. In RFI QKD, the stability of the Z basis can be well maintained, which is also the case in most other QKD systems, while the X and Y bases are allowed to vary slowly. That is, Alice and Bob’s Z, X, and Y bases satisfy Z_B = Z_A, X_B = cosβX_A + sinβY_A, and Y_B = cosβY_A − sinβX_A, where β is the relative rotation between Alice and Bob’s reference frames and may drift with time slowly. After the quantum communication phase, Alice and Bob can distill secret keys from the data in Z_AZ_B basis, and estimate Eve’s information from the data in X_AX_B, X_AY_B, Y_AX_B, and Y_AY_B bases. According to the decoy-state method,^[26] the total gain and quantum bit error rate (QBER) that Alice sends in ξ_A (ξ_A ∈ {X_A, Y_A, Z_A}) and Bob measures them in ξ_B (ξ_B ∈ {X_B, Y_B, Z_B}) in the decoy-state RFI QKD can be calculated by 1 2 where ε refers to the signal states μ, the decoy states ν, or the vacuum states ω, i denotes the i-photon states, P_ε(i) corresponds to the photon-number distribution for the ε intensity. ( ) denotes the QBER (the yield) of the i-photon states. According to Eqs. (1) and (2), Alice and Bob can estimate the yields (error rates) of single-photon contributions , , , , and ( , , , , and ) with the three-intensity decoy-state method. Then, they can estimate the quantity . Finally, Eve’s information can be bounded by 3 where and After the post-processing phase, the final key generation rate in the case of phase-randomized light sources with three-intensity decoy-state method can be calculated by^[20] 4 where ( ) represents the gain (QBER) of the signal states in Z_AZ_B basis, denotes the counting rate of the single-photon pulses from the signal states, h is the binary Shannon information function, and f is the error correction efficiency.

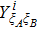
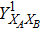
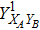
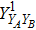
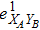
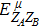
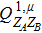
In practice, source errors and statistical fluctuations are inevitable issues in the security analysis of practical decoy-state RFI QKD systems. When considering source errors (for simplicity, we assume the vacuum source is precise which has no source errors), due to the imperfection of practical sources, the intensity of the pulses is not stable. That is to say, ε ranges from ε_L(δ) to ε_U(δ), where δ refers to the intensity fluctuations. Then, we can obtain the upper bound ( ) and the lower bound ( ) of the i-photon number distribution with intensity fluctuations. Take the WCS for example, 5 6 Then, the upper bounds (the lower bounds) of the total gain and QBER can be obtained respectively as follows: 7 8 {EξAξB,UεQξAξB,Uε=∑i=1∞eξAξBiYξAξBiPεU(i)+eξAξB0YξAξB0PεU(0),EξAξB,LεQξAξB,Lε=∑i=1∞eξAξBiYξAξBiPεL(i)+eξAξB0YξAξB0PεL(0). Finally, according to Ref. [32], the yield (error rate) of single-photon contributions in Z_AZ_B can be estimated by 9 10

The other parameters , , , and ( , , , and ) can be obtained analogously by applying the same method. According to the statistical fluctuations analysis theory,^[33–35] the total gain and quantum bit error should be modified as follows: 11 12 13 EξAξBν,UQξAξBν,U=EξAξBνQξAξBν.(1+γEξAξBνQξAξBνNPεPξA|εPξB),  where P_ε represents the probability that Alice randomly modulates pulses into the ε intensity, P_ξA|ε denotes the conditional probability that Alice sends the states to Bob in ξ_A basis with the ε intensity, P_ξB refers to the probability that Bob chooses the ξ_B basis for his measurement, γ is the number of standard deviation, and N refers to the total number of pulses.

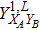
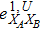
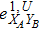
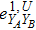
In order to explore the performance of the above decoy-state RFI-QKD scheme under practical experimental conditions, we use two kinds of light sources, e.g., WCS^[3,4] and HSPS,^[27,28] as examples and carry out the corresponding numerical simulations.

For the WCS, it has a Poisson distribution: , (i ∈ (1,2,3,…)), while for the HSPS, it follows a sub-Poisson distribution: , where η_A and d_A each correspond to the detection efficiency and the dark count rate of the local detector at Alice’s side.

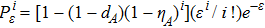
In all the simulation results presented below, we use the following parameters: ν = 0.01, ω = 0, P_μ = 1/2, P_ν = P_ω = 1/4, and P_XA = P_YA = P_ZA = P_XB = P_YB = P_ZB = 1/3. Moreover, we set the misalignment of the reference frames as β = π/7 (in fact, β is unknown and we just use it to simulate a practical RFI-QKD system). Other parameters used in the simulation are listed in Table 1. For each line, the intensity of the signal states is optimized at each distance to maximize the final key rate.

Table 1.

Table 1.

Table 1. Simulation parameters for the three-intensity decoy-state RFI QKD with both source errors and statistical fluctuations. ηd (Y0) is the detection efficiency (the dark count rate) of Bob’s single photon detectors, ed is the probability that Bob’s single-photon detector is clicked incorrectly. α denotes the loss coefficient of the standard fiber link, γ is the number of the standard deviation when considering statistical fluctuations (here 5.3 corresponds to a failure probability of 10−7), and f is the error correction efficiency. ηA (dA) is the detection efficiency (the dark count rate) of Alice’s single photon detector with HSPS. . ηd ed Y0 α/(dB/km) ηA dA γ f 14.5% 1.5% 3 × 10−6 0.2 0.75 1 × 10−6 5.3 1.16

Table 1. Simulation parameters for the three-intensity decoy-state RFI QKD with both source errors and statistical fluctuations. ηd (Y0) is the detection efficiency (the dark count rate) of Bob’s single photon detectors, ed is the probability that Bob’s single-photon detector is clicked incorrectly. α denotes the loss coefficient of the standard fiber link, γ is the number of the standard deviation when considering statistical fluctuations (here 5.3 corresponds to a failure probability of 10−7), and f is the error correction efficiency. ηA (dA) is the detection efficiency (the dark count rate) of Alice’s single photon detector with HSPS. .

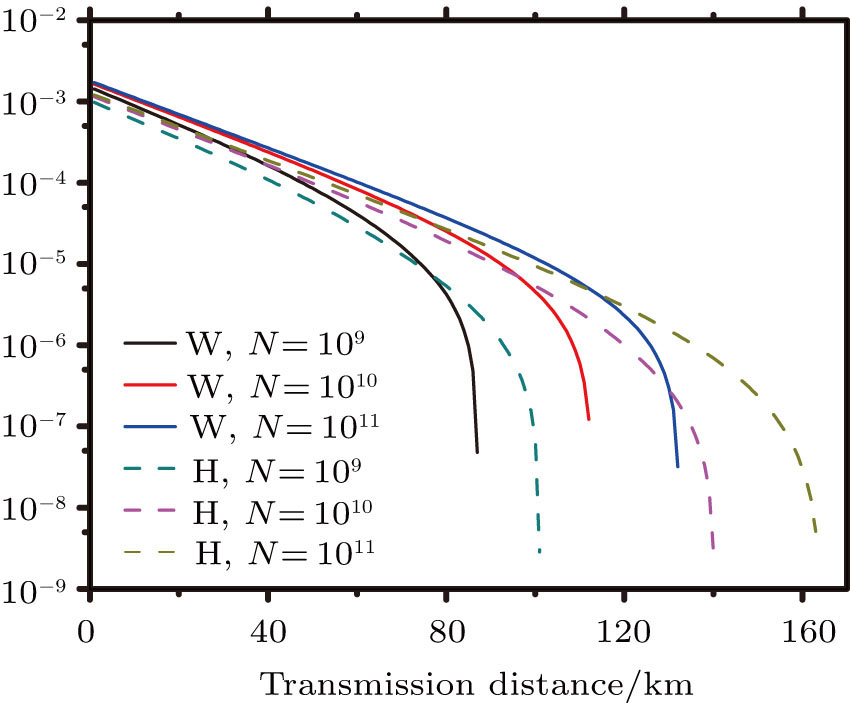
First, we study the performance of the decoy-state RFI QKD with standard statistical fluctuations, and the corresponding results are shown in Fig. 1. In Fig. 1, W (H) denotes WCS (HSPS), and the solid (dashed) curves from left to right correspond to the secret key rates of the decoy-state RFI QKD with WCS (HSPS) at N = 10⁹, 10¹⁰, and 10¹¹, respectively. From Fig. 1, it can be easily seen that the secret key rates of WCS are higher than those of HSPS in short distance range, but the key rates of HSPS outperform WCS in long distance range.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) Comparison results of the decoy-state RFI QKD with WCS and HSPS when considering statistical fluctuations. The solid (dashed) curves from left to right refer to the secret key rates of the decoy-state RFI QKD using WCS (HSPS) with N = 109, 1010, and 1011, respectively.

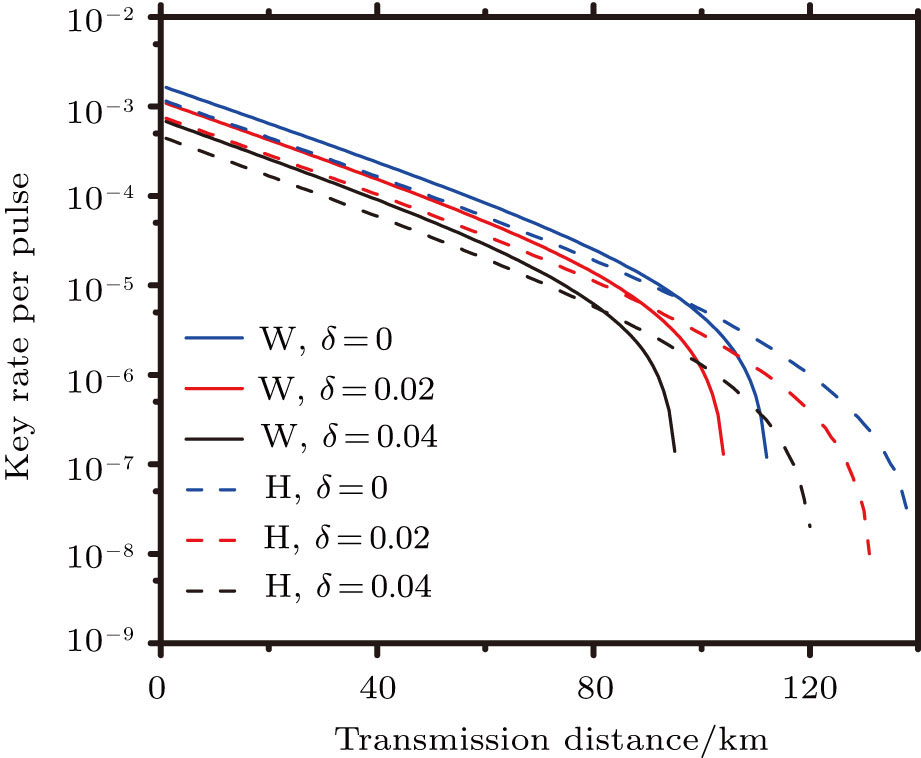
Then, we consider the effect of different source errors in the decoy-state RFI QKD with statistical fluctuations (N = 10¹⁰), and the simulation results are shown in Fig. 2. Here, W (H) denotes WCS (HSPS), and the solid (dashed) curves from left to right in Fig. 2 denote the key rates of WCS (HSPS) with source errors δ = 0.04, 0.02, and 0, individually. From Fig. 2, we find that the secret key rate declines with the increasing of source errors for both HSPS and WCS. Moreover, RFI QKD with WCS shows better performance than the one using HSPS at short distance range (< 80 km), and presents lower secret key rate than the one using HSPS at long distance range (> 110 km).

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) Comparison results of the decoy-state RFI QKD with source errors when the number of sent pulses is N = 1010. The solid (dashed) curves from left to right denote the secret key rates of the decoy-state RFI QKD with WCS (HSPS) with δ = 0.04, 0.02, and 0, respectively.

Finally, the optimal intensities of signal states and the corresponding key rates at 60 km with statistical fluctuations and with both statistical fluctuations and source errors are shown in Table 2 and Table 3.

Table 2.

Table 2.

Table 2. The optimal intensities of signal states and corresponding key rates at 60 km with statistical fluctuations. . Par W H N = 109 N = 1010 N = 1011 N = 109 N = 1010 N = 1011 μ 0.539 0.653 0.684 0.482 0.596 0.629 R 4.080 × 10−5 8.327 × 10−5 1.017 × 10−4 2.873 × 10−5 5.858 × 10−5 7.182 × 10−5

Table 2. The optimal intensities of signal states and corresponding key rates at 60 km with statistical fluctuations. .

Table 3.

Table 3.

Table 3. The optimal intensities of signal states and corresponding key rates at 60 km with both statistical fluctuations and source errors. . Par W H δ = 0 δ = 0.02 δ = 0.04 δ = 0 δ = 0.02 δ = 0.04 μ 0.653 0.626 0.566 0.596 0.554 0.482 R 8.327 × 10−5 5.163 × 10−5 2.855 × 10−5 5.858 × 10−5 3.598 × 10−5 1.981 × 10−5

Table 3. The optimal intensities of signal states and corresponding key rates at 60 km with both statistical fluctuations and source errors. .

In conclusion, RFI QKD can generate secret keys without alignment of reference frames, which exhibits obvious superiority in real-life QKD systems. Considering both source errors and statistical fluctuations, we studied the performance of the decoy-state RFI QKD with two kinds of practical sources, e.g., WCS and HSPS. Simulation results demonstrate that the secret key rates of the decoy-state RFI QKD with WCS are higher than those with HSPS in a short distance range, but the secret key rates of RFI QKD with HSPS outperform those with WCS in a long distance range. Our work will provide useful guidance in practical implementations of RFI QKD systems.