† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 51401001, 51371002, and 51331003) and the International S&T Cooperation Program of China (Grant No. 2015DFG52020).
Magnetic properties and magnetization processes of Co nanowire arrays with various packing densities are investigated by means of object-oriented micromagnetic framework (OOMMF) software package with finite difference micromagnetic simulations. The packing density of nanowires is changed with the diameter, number of nanowires and center-to-center spacing between the wires. The magnetization reversal mechanism and squareness of the hysteresis loops of the nanowire arrays are very sensitive to the packing density of nanowires. Clear steps and plateaux on the demagnetization are visible, which turns out that dipolar interactions among the wires have a significant influence on switching field.
The magnetic properties of the 3d metal and alloy magnetic nanowire array have been extensively investigated because of their potential applications in ultrahigh-density magnetic recording media and future permanent magnets.[1–8] Kittel first obtained the high coercivity in cobalt particle resulting from shape anisotropy through calculations.[9] Nowadays, advances in fabrication techniques, such as polyol method, have allowed the preparation of nanostructured systems with very interesting physical properties. Pousthomis et al. prepared Co nanorods with mean diameters ranging from 7–25 nm and lengths ranging from 30–300 nm by the polyol method, and a high coercivity of 7.2 kOe was obtained for Co nanorods with a mean diameter of 9 nm.[10] Anagnostopoulou et al. prepared Co rods and assembled them from wet suspensions under a magnetic field, and the magnets prepared with the rods assemblies exhibited energy product, (BH)max exceeding 18.85 MGOe.[11] However, the theoretically predicted upper limit of the coercivity and the maximum energy product of single Co nanowire are 16.6 kOe (1/2μ0Ms + Ha) and 81 MGOe, respectively.[12] There is still a potential to obtain larger coercivity and energy product for Co nanowires. Further theoretical studies on magnetic properties of Co nanowires have been carried out. Westphalen et al. have studied the magnetization reversal in nanowires with a spiral shape and found that the magnetization reversal is rather inhomogeneous.[13] Vila et al. have studied the magnetic vortex in nanowire with transverse easy axis.[14] Ott et al.[15] and Zighem and Mercone[16] have independently studied the effect of the shape of elongated magnetic particles on the coercivity.[15,16] Note that the effective dipolar interactions among the nanowires have a strong influence on the macroscopic magnetic behavior of the system.[17] Nevertheless, the details of the magnetization processes occurring in arrays of closely packed magnetic nanowires are still unknown.
In this paper, the effects of dipolar interaction on the coercivity and energy product of the Co nanowire assemblies with the micromagnetic simulations and the mechanism of the magnetization reversal process of nanowires array are investigated.
Systematically, the effects of the dipolar interaction on magnetic properties and magnetization processes in array of Co nanowires are investigated using OOMMF micromagnetic simulations.[18–20] These simulations are performed with an algorithm-based finite difference method. Equilibrium structures of the magnetization are characterized by local energy minima. The total energy Etot of a given arrangement of the magnetization in a ferromagnetic sample reads
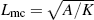
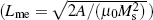
Figure
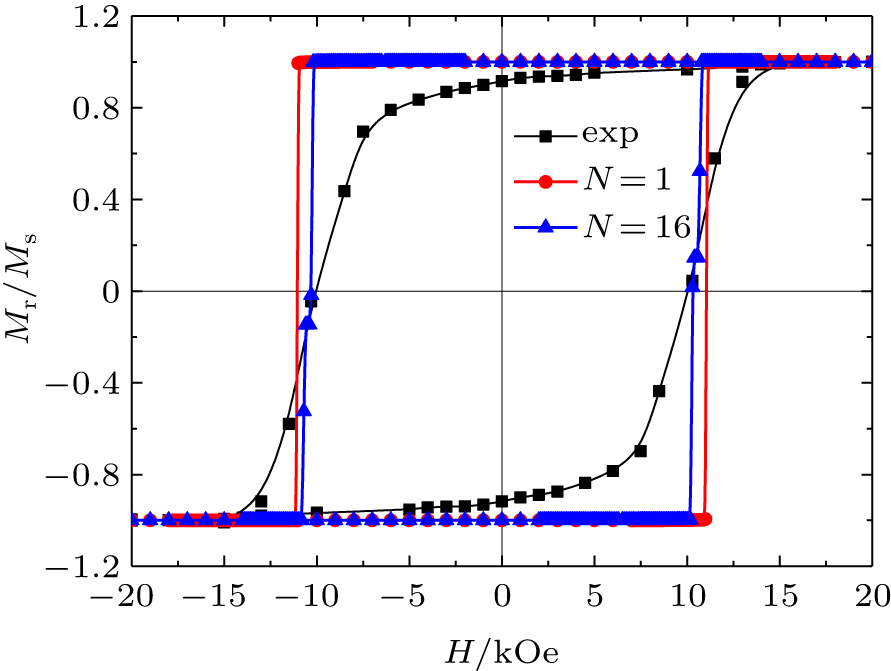 | Fig. 1. (color online) Experimental[12] and simulated hysteresis loops with the field applied parallel to the long axis for Co nanowires assemblies. The red line with circles represents the hysteresis loop of one Co nanowire for comparison. |
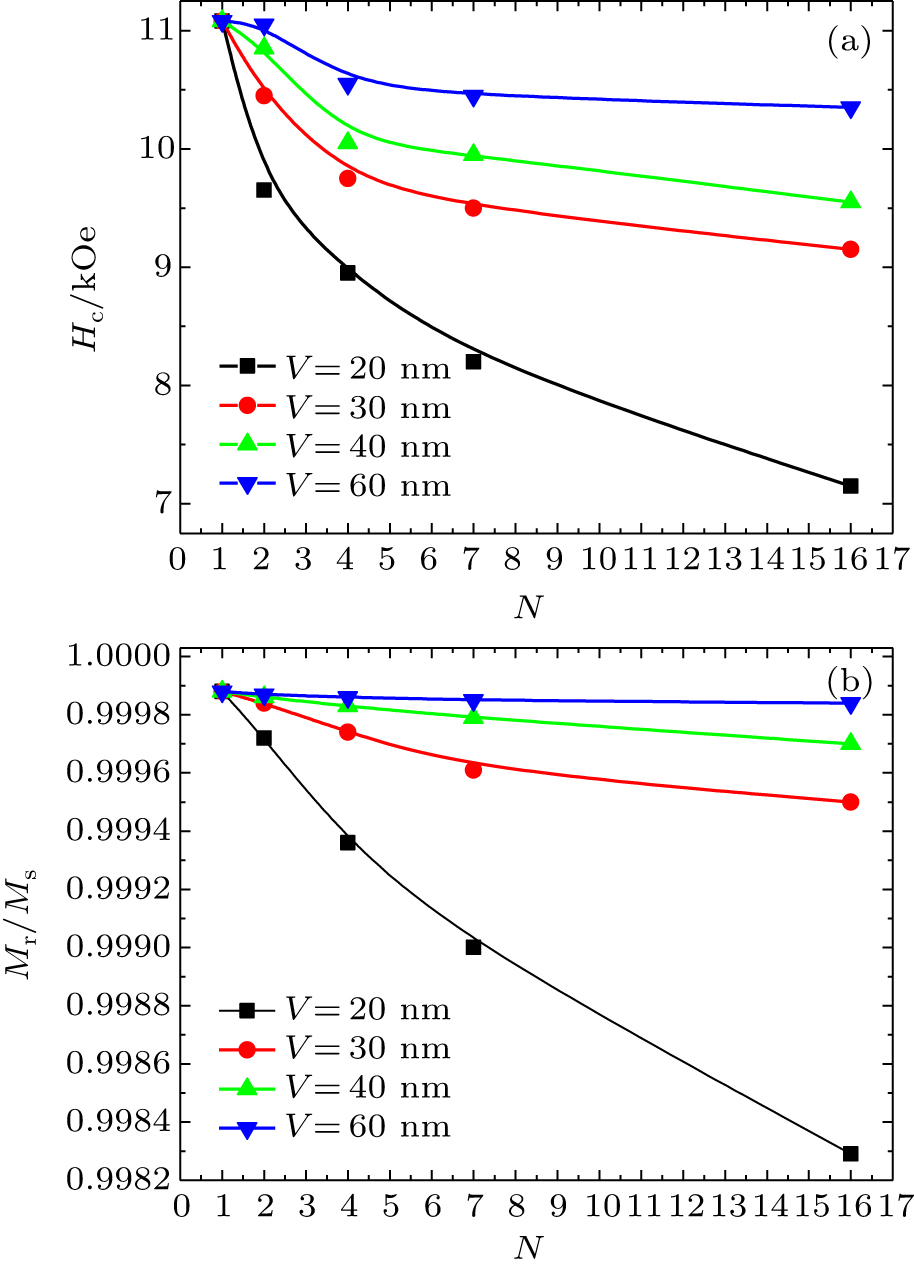
To further understand the dipolar interactions in Co nanowires array, a systematic simulation for different numbers of nanowires and various center-to-center interspaces between the wires is analyzed. To compare with the experimental result, nanowire diameter is set to be a constant value D = 15 nm. The magnetic measurement sample consists of a large array of magnetic nanowires, however, the maximal size of the simulated array is not sufficient to expect an exact reproduction of the experimental value. Modeling an array with macroscopic dimensions is impracticable compared with experimental value due to the long computational time of calculation. In order to account for the interaction between the neighboring wires in the simulation, the hysteresis loops with up to 16 interacting nanowires are simulated, which is the largest set used in the calculation.[21] Figure
It is already well known that the dipolar interactions affect considerably the macroscopic magnetic behavior of array of nanowires. High packing fraction for nanowires assemblies is an important factor for obtaining a high energy product. However, high packing fraction for nanowire assembly results in lower coercivity. Thus, the optimal packing density is very important for obtaining high magnetic energy product and coercivity. For this purpose, Co nanowire arrays with various packing densities are simulated and the numbers of nanowires (N = 16) in all nanowire arrays are also fixed. The coercivity increases with the decrease of diameter and the increase of aspect ratio, which is in good agreement with the enhanced shape anisotropy.[15] For fixed diameter of nanowires, coercivity decreases with the increase of the packing density. The ideal (BH)max of 46.43 MGOe is obtained for an array by combining a high packing density (P = 0.628) and a small diameter (D = 10 nm) as shown in Fig.
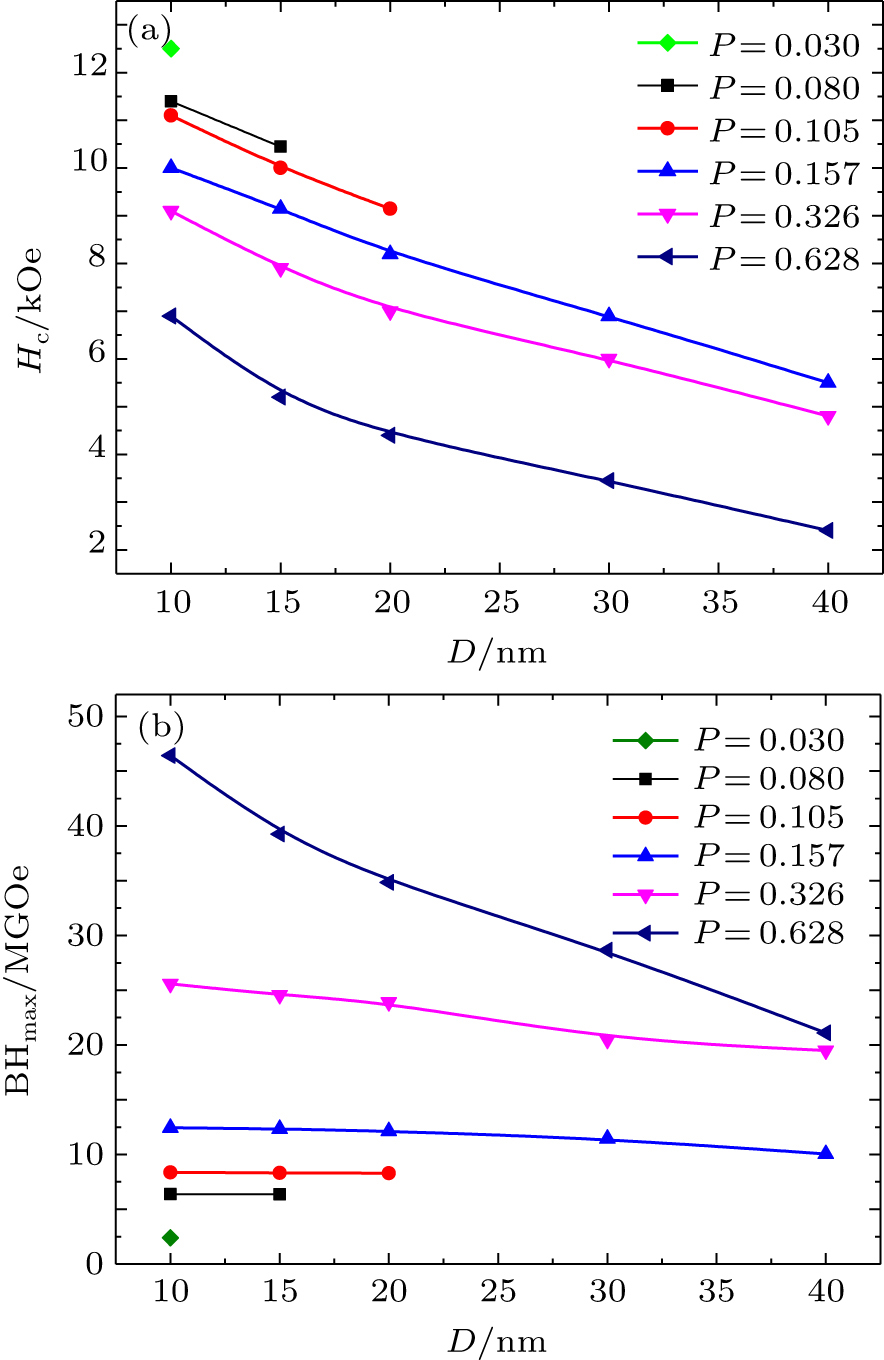 | Fig. 3. (color online) (a) Coercivity and (b) magnetic maximum energy product of nanowires array with different values of diameter (D) and packing density (P), the numbers of nanowires (N) is 16. |
Obviously, the higher the packing density, the stronger the magnetostatic interaction among the Co nanowires will be. Increasing the distance of center-to-center spacing between the wires from 20 to 60 nm while keeping the diameter of the wires at 15 nm and number of nanowires at 16, the remanence ratio increases up to nearly 1 and the coercivity rises from 7.2 kOe up to 10.4 kOe as shown in Fig.
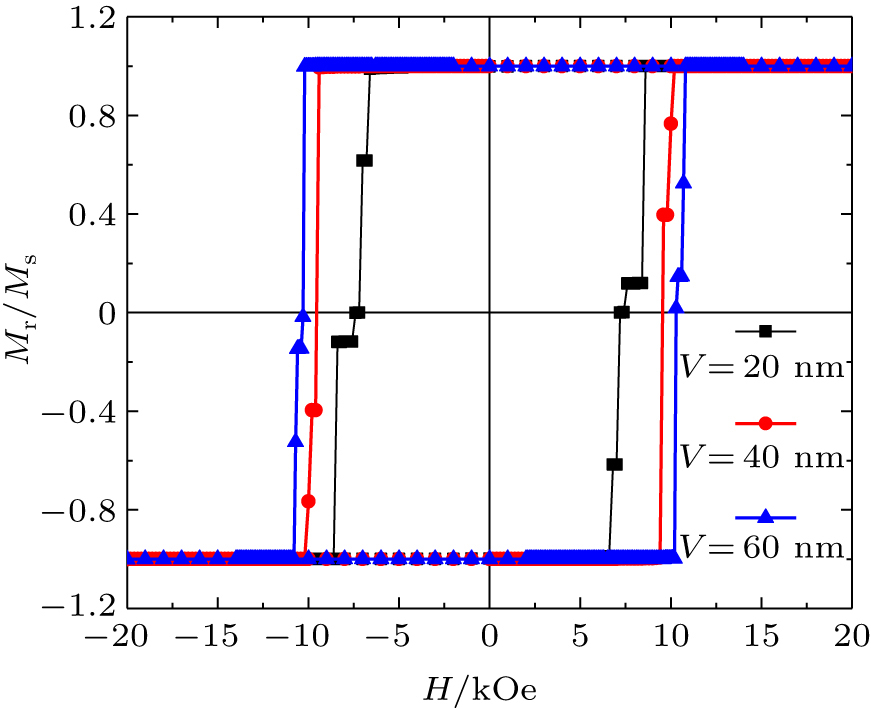 | Fig. 4. (color online) Hysteresis loops of arrays with different center-to-center spacing between the wires. The numbers of nanowires (N) is 16 and the diameter of nanowires (D) is 15 nm. |
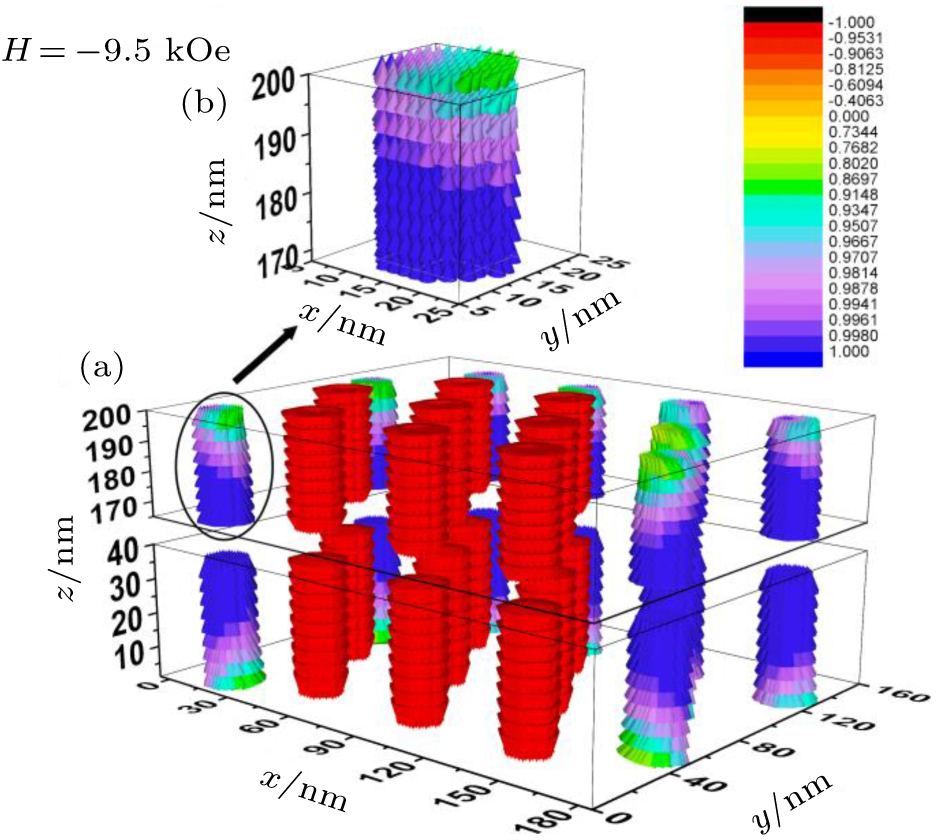
We investigate magnetization configuration of one nanowire array (D = 15 nm, V = 40 nm) as shown in Fig.
The magnetic properties and magnetization processes of the Co nanowires array with various packing densities are investigated by means of micromagnetic simulation. The magnetization reversal mechanism and coercivity of the nanowires are very sensitive to the packing density of nanowires. The effects of dipolar interaction on the coercivity and the energy product of nanowires array are enhanced with the increasing of packing density. The magnetization reversal mechanism plays a major role in squareness of the hysteresis loops in nanowires array. The results can be explained considering the dipolar field created by the neighboring nanowires. It is clearly shown that this field is responsible for the change of the reversal field of the wires, leading to the occurrence of plateaux in the demagnetization process.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |