† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 10947004) and the Government Scholarship for Overseas Studies of Jiangsu Province, China.
Connecting one armchair carbon nanotube (CNT) to several zigzag graphene nanoribbons (ZGNRs) we find that the topologically-protected edge states of ZGNRs and the massless Dirac particle inherited from CNT still hold from the analysis of the band structure and the edge state. Furthermore, the lowest conductance step at the valley bottom increases proportionally with increasing the number of ZGNR wings. A novel conductance step of a peak occurs in the valley, which is two steps higher than the lowest step at the valley bottom. In addition, with increasing the number of ZGNR wings the width of the novel conductance step becomes narrow.
Since the discovery of carbon nanotubes (CNTs)[1] and the groundbreaking experiments regarding the monolayer graphene,[2] the low-dimensional carbon nano-material has been considered a promising material for future electronics. Extensive experimental and theoretical researches have been devoted to the studying of their various novel physical properties. The subsequent experimental measurement on graphene layers motivates the investigation on the spin quantum transport in graphene.[3,4] Recently, topological surface states (edge states) in condensed matter have received a lot of attention; specially zigzag-edged graphene nanoribbons (ZGNRs) have recently received significant attention due to their unique spin-related electronic structures and the topologically-protected edge states.[5–11] One proposed that the quantum spin Hall effect (QSHE)[12–15] can occur in the topological insulators (TIs) without applying any magnetic field.[16–22] Nowadays, many experimental and theoretical studies focus on looking for new two-dimensional layered materials in order to obtain new two-dimensional TIs having large bulk energy gaps for QSHE in practice. Recently many new two-dimensional TIs have been found such as HgTe/CdTe,[16] InAs/GaSb,[17] and Cd3As2[18] quantum-well structures, Bi2TeI,[19] the bismuth (111) bilayer,[20] and the simple binary compounds ZrTe5 and HfTe5.[21,22] However, by using the known two-dimensional TIs, the assembled quasi-one-dimensional materials have been studied little, especially using two-dimensional graphene. In 2015, Weng et al. proposed three-dimensional graphene networks with negative curvature having topologically nontrivial node lines in bulk based on the first-principle calculations.[23] Obviously, the assembled carbon nanomaterials (ACNMs) can help us develop many possible ways to construct new artificial materials or devices with many more expected function effects.
These ACNMs have stable geometrical structures and can be produced artificially due to the various bond configurations of a carbon atom connecting to its neighbor atoms. In the present work, we try to assemble armchair CNTs together with ZGNR slices as a new type of quasi-one-dimensional carbon nanomaterial. We can optimize it by using the empirical potential and the first-principle calculations. We think that these ACNMs have not only the merit characters inherited from both CNTs and graphene, but also some novel effects due to the existence of the sp3 hybrid bonds connecting the CNT with the ZGNRs.
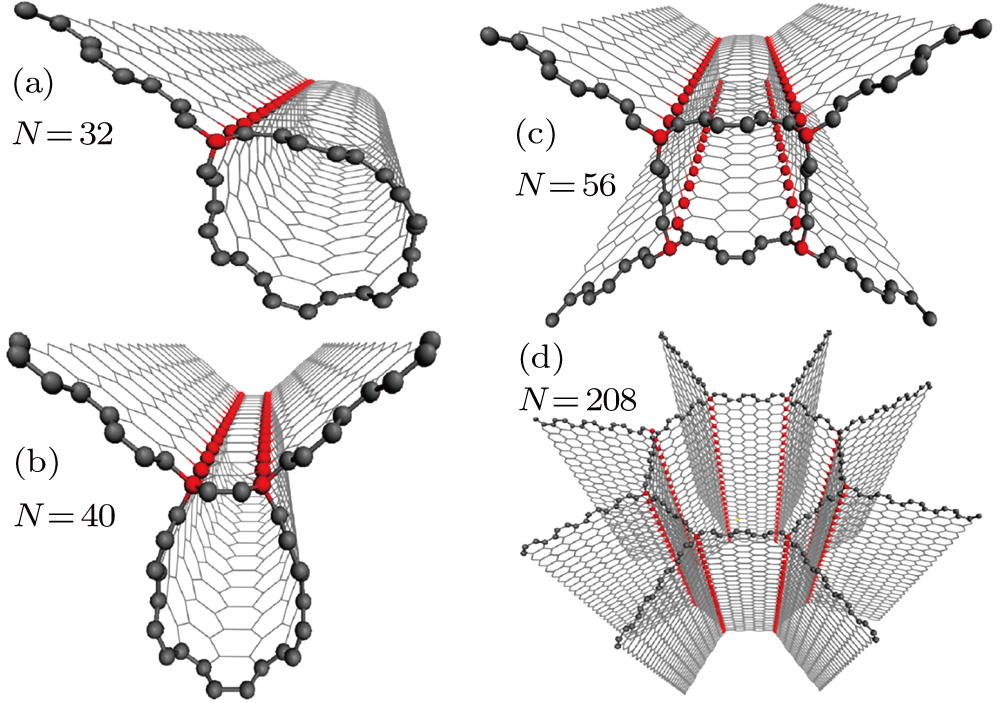
As is well known, the ZGNRs have the topologically-protected edge states, and an armchair tube has two Dirac points, so we are interested in using ZGNR and one armchair tube as the elements to build up ACNMs, called CNT with wing-like ZGNR slices (ZW-CNT). In Fig.
Within the π-electron tight-binding method only considering the nearest neighbors, the band structures of various ZWn-CNT are shown in Fig.
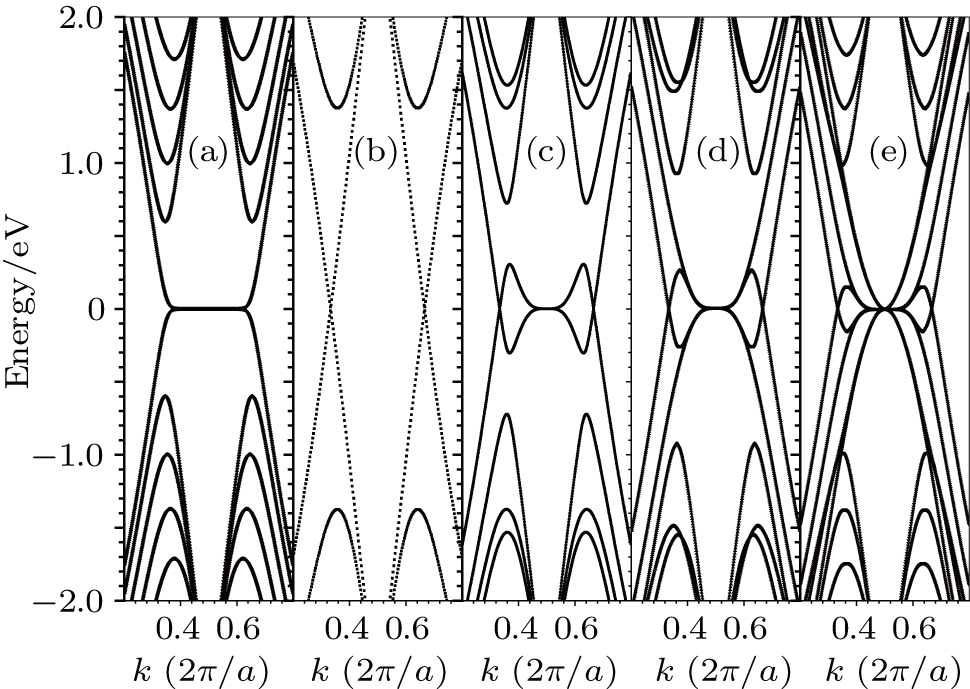 | Fig. 2. Band structures of various ZW-(6, 6), i.e., (a) ZGNR (N = 40), (b) CNT (6,6), (c) ZW1-(6,6), (d) ZW2-(6,6), and (e) ZW4-(6,6). Tube (6,6) and ZGNR (N = 40) given here are for comparison. |
Naturally, in the energy region away from the zero energy point, the band structure of ZW2-(6,6) is similar to that of the pure ZGNR under the condition of the same size (N = 40). However, some obvious differences are found in the energy region of interest, near the zero energy. No matter how many wing-like ZGNR slices are connected to the tube (6, 6), the two Dirac points at ±1/3 inherited from armchair tube (6, 6) still hold. Furthermore, between the two wave vector points −1/3 and 1/3, the bands through the Dirac points change direction and go back to zero energy, and the states become edge states, which are shown in Fig.
Another remarkable feature is that the number of bands drifting into the zero energy increases proportionally with the number of wings increasing.
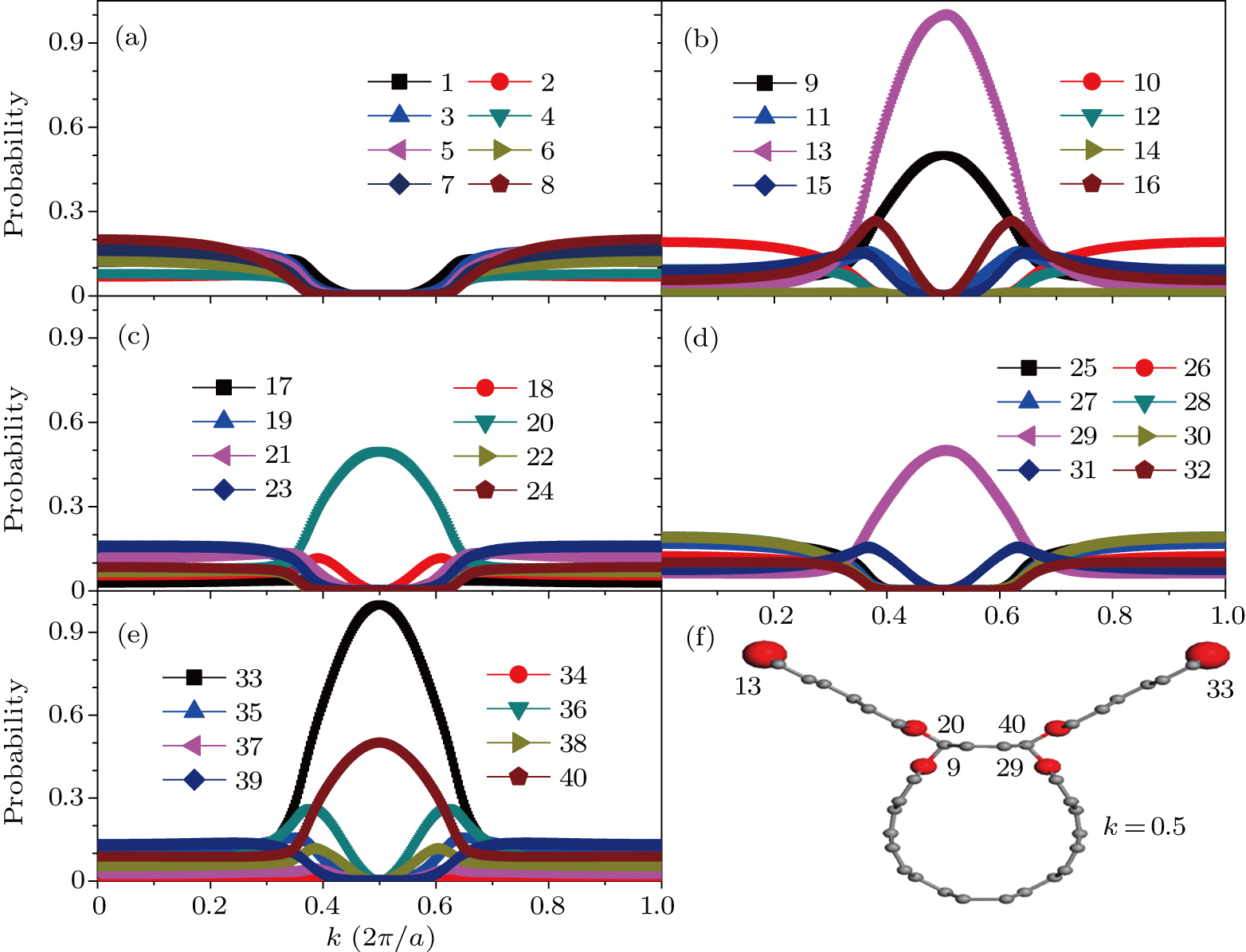
Considering no spin degree, at the zero energy the numbers of bands are 2, 4, and 8 for ZW1-(6, 6), ZW2-(6, 6), and ZW4-(6, 6), respectively. Taking the ZW2-(6, 6) for example, in order to illustrate the edge-distribution characteristics of the states in these four bands drifting to the zero energy, in Figs.
On the opposite-direction edge side of the ZGNR slice, that is to say, at the connection place, the probability distribution is different from that in the case of the pure ZGNR. At the sites 9, 20, 29, and 40, denoted by the relatively small red balls in Fig.
By use of the Landauer formula and Green’s function method[24–28] the quantum conductance through a region of interacting electrons can be calculated and is shown in Fig.
Specially, in the energy region from −1 eV to 1 eV, of interest, there is one novel higher quantum conductance step at the lowest valley for any curve of ZWn-(6, 6). In the present theoretical model no matter how large the sizes of ZGNR and the armchair tube are, their lowest conductance steps are always 1 and 2, respectively. However, the lowest conductance steps are 1, 2, and 4 for ZW1-(6,6), ZW2-(6,6), and ZW4-(6,6), respectively, showing that it is not the summation of the lowest steps of CNT and ZGNR slices. That is to say, the lowest conductance step of ZWn-CNTs is n, which is the number of ZGNR wings.
Remarkably, at the valley bottom there are novel higher conductance steps 3, 4, and 6 for ZW1-(6,6), ZW2-(6,6), and ZW4-(6,6), respectively, which is two steps higher than the corresponding lowest conductance step. Obviously, this increase of two channels for these novel conductance steps originates from the armchair tube. Furthermore, with increasing the number of ZGNR wings the width of the novel conductance step becomes narrower in Fig.
In our study, for the assembled ZW-CNTs two Dirac points still hold and the topologically-protected edge states of ZGNRs exist. We find that the lowest conductance step in the valley is attributed to the edge states of all connected ZGNR slices. Furthermore, because the bands through the Dirac points change direction to the zero energy, and the states become edge states at k = 0.5, there are two channels increased that contribute two conductance steps higher than the lowest step of the valley bottom. Finally, with increasing the number of wings, the width of the novel higher conductance step at the valley bottom becomes narrow, the number of edge bands increases, and the corresponding lowest quantum conductance step increases proportionally.
Obviously, for this assembled quasi-one-dimensional ZWn-CNT the conductance in the lower energy region is higher than that for the single CNT or a pure ZGNR. Specially, the existence of the novel higher conductance step at the zero energy can help us to design a more precisely-controlled nanoswitch. Furthermore, due to there being much more atoms in the primitive cell and lower symmetry than those in CNT or ZGNR, it has super strong dipole matrix elements along the axis direction. Naturally, the strong nonlinear optical susceptibility and novel optical effect can be imaged for the incident light polarized along the axis direction. Therefore, in practical applications, we believe that this assembled method provides a way to build various quasi-one-dimensional or quasi-three-dimensional all-carbon nanomaterials for more precisely-controlled nanodevices working in the lower energy region, such as sensitive optoelectronic nanoswitches, thermoelectronics, supercapacitors, hydrgon storage, absorbents, and strong nonlinear optical devices. We will carry out detailed research in the future in order to give a new in-depth insight into the characteristics of edge states and the various properties in this type of ACNM.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] |