† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2013CBA01503) and the National Natural Science Foundation of China (GrantNo. 11103040).
Laser-driven ramp compression was used to investigate iron characteristics along the isentropic path. The iterative Lagrangian analysis method was employed to analyze the free surface velocity profiles in iron stepped target measured with two VISARs. The onset stress for the α to ε phase transformation was determined from the sudden change in the sound velocity and was found over-pressurized compared to the static and shock results. The derived stress (26 GPa) and strain rate (up to 108 s−1) are consistent with our previous experimental results. The stress–density relations were compared with those from previous ramp experiments and good agreements were found, which experimentally confirms the simulations, showing that iterative Lagrangian analysis can be applied to the ramp-compression data with weak shock.
During the last two decades, several planets were discovered around some stars outside the solar system; mass and radius were the main collected information. Deducing planet compositions and internal structure from the mass–radius relation is very often the only possibility to study the physical properties of these extrasolar planets, but this method depends greatly on the equation of state of a planet’s constituent materials.[1] Thus properties of matter at pressures up to 70 Mbar and temperatures up to 20000 K are essential to determine the formation process and internal structure of such planets,[2] of which iron is one of the most important materials and thought to be the main composition element in the core.[3] Over recent decades, the study of matter under extreme conditions has been extended greatly, in both pressure and strain rate, with rapid development of the large pulse power facilities, such as Z-pinch[4] and large laser facility.[5,6] New developments in static compression methods have also raised the limit of available pressure. For example, the highest pressure for metal osmium can reach 750 GPa with conventional and double-stage diamond anvil cells.[7] Also, ramp compression methods have been used to compress matter to pressure and temperature conditions not available with former shock methods and study matter under variable strain rates. Ramp compression with laser was first demonstrated by Edwards et al. in 2004,[8] where laser energy was converted to expanding plasma to load ramp wave on the target. Since then, study of the properties of materials under isentropic conditions, such as the equation of state, the phase transformation, and the elastic response, has been carried out widely.[9–13]
In this context, the dynamics of phase transition at high strain rates is particularly interesting. The iron body-centered-cubic [bcc] phase to hexagonal-closed packed [hcp] phase transformation was first discovered in 1956[14] and this phenomenon was studied afterwards both in static and shock experiments.[15–17] Recently, Smith et al.[18] investigated iron with ramp compression methods on laser facilities and the Sandia Z-machine. In their work, the strain rate reached 108 s−1. By combining their experimental results and previous experimental data, they found a rapid increase in the onset pressure of phase transition when the strain rates are higher than 106 s−1. Laser-driven ramp compression with the compression rate of about 107 s−1 was reported by Amadou et al.[19,20] and explained the pressure overshoot in the context of phase nucleation and growth theory with an isokinetic strain rate regime. Laser-driven isentropic compression is trying to reach the highest pressure with the laser facility under its available parameters, such as energy and pulse width. The key challenge is to avoid the shock formation during compression process, while shock is thermodynamically inevitable when the high pressure sound waves catch up with the low pressure sound waves for a target of infinite thickness. Thus experiments must be carefully designed to make this “catch up” happen on the rear surface of the target. Since the sound wave velocities at different pressures are not exactly known, and the laser intensity cannot be arbitrary changed, it is difficult to achieve the isentropic compression with direct laser-driven method. Generally, ramp compression data at these high rates are relatively rare.
In this paper, laser-driven ramp compression is employed to study iron under isentropic conditions. In earlier ramp compression experiments, laser energy was usually converted into x-ray Planck radiation by irradiating a hohlraum,[21] or the expanding plasma of a plastic reservoir was used to achieve ramp compression.[22] In our experiment, we have chosen a more efficient way, irradiating the sample directly with a temporally shaped laser pulse.[23] A signature of the α-phase to ε-phase transition is observed at 26 GPa. This pressure is much higher than that observed in static and shock experiments (13 GPa).[14,15] The compressive strain rates in our experiment are up to 108 s−1. The present results are consistent with our previous work, where these over pressurizations were observed and well explained using the phase nucleation and growth theory with an isokinetic regime for the strain rates ranging from 3 × 107 s−1 to 9 × 107 s−1.[20] Comparison of stress–density relations with other ramp experiments is made, and good agreements are found. The layout of the article is as follows. The experiment setup is described in Section
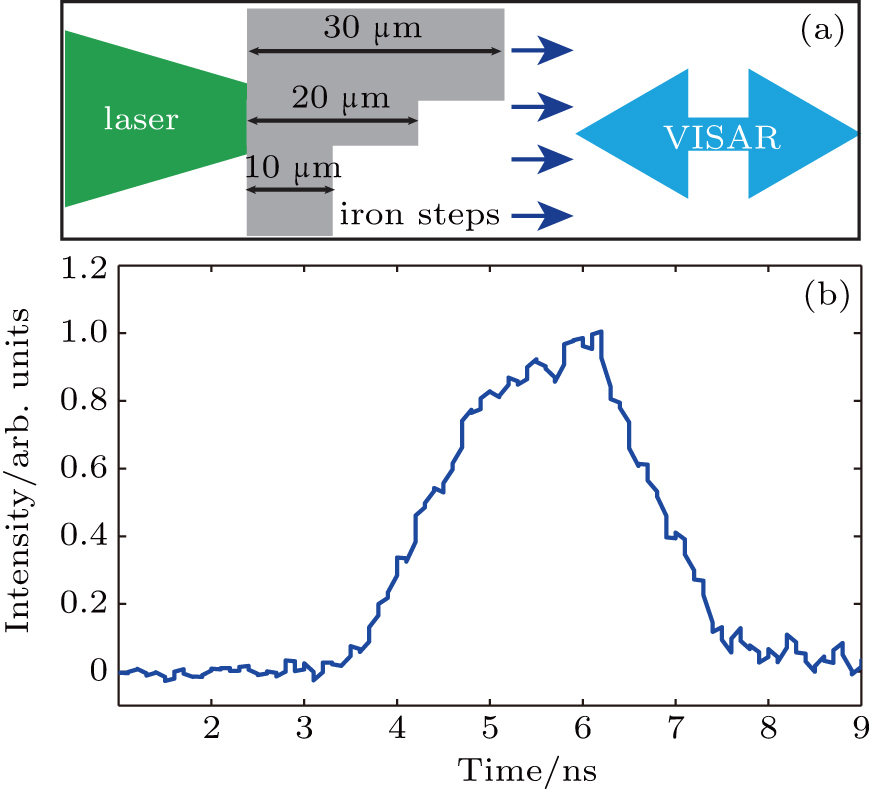
The experiment was performed at the LULI2000 laser facility, which can deliver a total energy of 400 J with pulse duration of up to 5 ns at wavelength of 532 nm. To achieve the ramp compression, shock must be avoided. Thus the laser pulse intensity has to be adjusted to increase smoothly.[24] In our experiment, the laser pulse shape was optimized to an exponential shape instead of linear shape based on the theoretical model.[25,26] This is similar to our previous ramp experiments.[19,20,27] A 1 mm diameter flat intensity profile of laser was obtained by using the hybrid phase plate (HPP). Targets were free standing iron foils with steps of 10/20/30 μm thicknesses. The iron was a polycrystalline rolled foil acquired from Goodfellow. The schematic diagram of the experiment setup and the measured laser pulse shape are shown in Fig.
To measure the rear surface velocity of the iron target, two velocity interferometer systems for any reflector (VISARs) were used to eliminate the ambiguity in case of a fringe jump. Etalons with different thickness were used to provide different velocity sensitivities for the two VISARs. The velocity-per-fringe (VPF) constants of the two VISARs are 0.992 km/s and 1.653 km/s. The temporal and spatial resolutions are 100 ps and 10 μm, respectively. The velocity profiles from the two VISARs agree well. The VISAR uses a probe laser beam delivering 1 mJ with 8 ns full width half maximum pulse length at a wavelength of 532 nm. It is independent of the drive laser and can have a variable delay relative to the drive laser. Furthermore, a streaked optical pyrometer (SOP) was used to record thermal emission from the rear surface of the iron target. As expected for isentropic compression, the temperatures were below the detection threshold of the diagnostic equipment (approximately 4000 K).
The raw image and velocity profiles of the iron’s rear surface measured with two VISARs are shown in Fig.
The iterative Lagrangian analysis,[29,30] that is, Lagrangian sound speed analysis combined with the iterative characteristic corrected method, is employed to analyze the experimental data. In Lagrangian analysis, a simple wave is assumed and the sound velocity is calculated by CL(u) = (Z2 − Z1) / (T2(u) − T1(u)), where Z2 and Z1 are the thicknesses of two steps, respectively, T2(u) and T1(u) are the arrival time with a particle velocity u at the two step rear surfaces. Then the stress and the volume can be obtained by integrating the following equations:
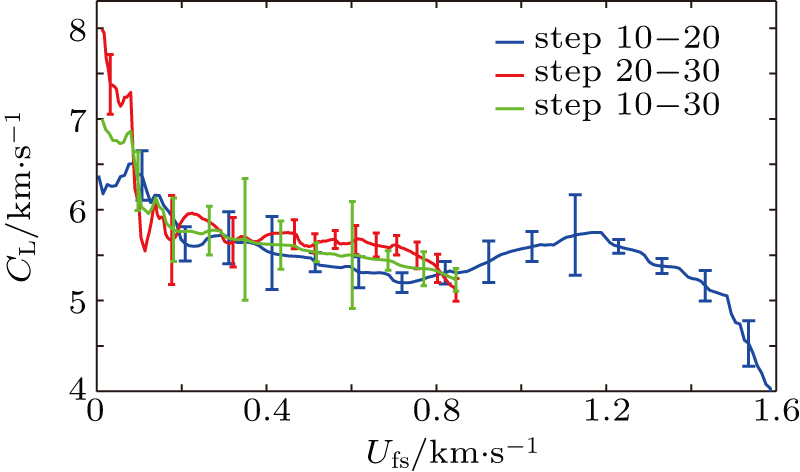 | Fig. 3. (color online) Lagrangian sound velocity calculated by different steps as a function of the rear free surface velocity. The error bar shows the uncertainties of the sound velocity. |
Figure
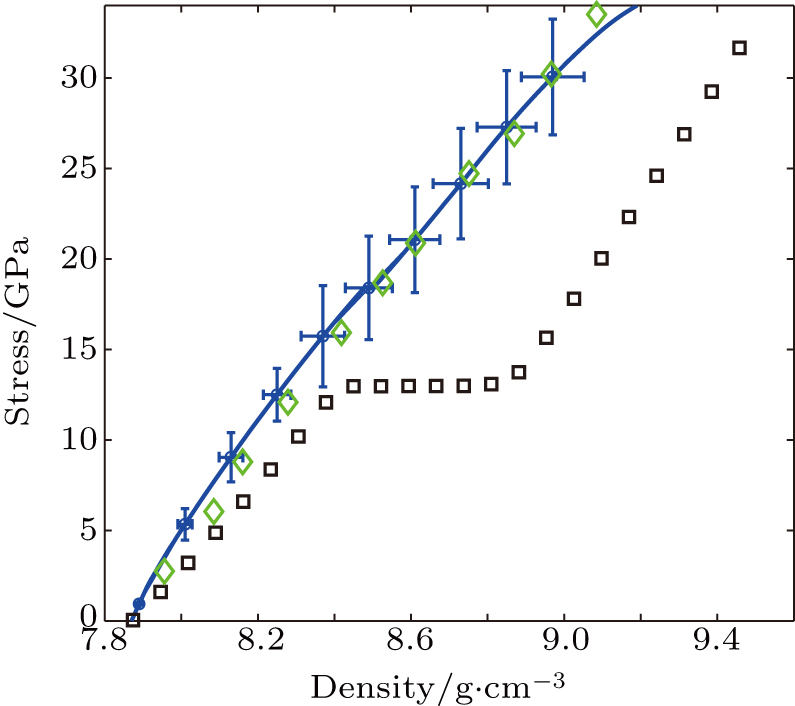 | Fig. 4. (color online) Stress–density relations calculated from our experiment (blue curves with error bars). Also shown are the stress–density data from SESAME (black squares) and Wang et al. (green diamonds).[21] |
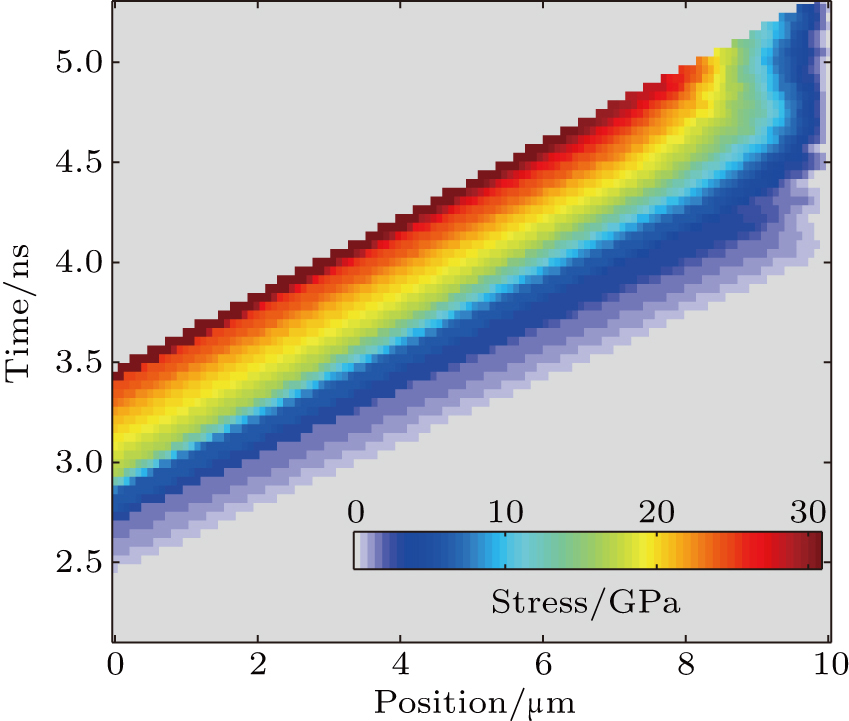
The stress distributions along the time and Lagrangian position in the iron, calculated from the iterative Lagrangian analysis, are shown in Fig. 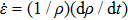
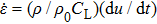
We have investigated the iron properties under ramp compression by directly irradiating the sample with a profiled laser pulse. The free surface velocity profiles of an iron step target measured by VISAR were analyzed with iterative Lagrangian analysis, and the stress–density relations were determined. Our data is in excellent agreement with other ramp compression experiments. This is the first experiment demonstrating that iterative Lagrangian analysis can be applied even if shock occurs in the ramp compression. Strain rates up to 108 s−1 were achieved in our experiment and the onset stress for α–ε phase transition was found to be over pressurized, in accordance with our previous experimental results[20] and those from Smith et al.[18] The data presented here together with our previous data[20] are a good supplement to experimental data of strain rates greater than 107 s−1.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |