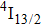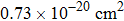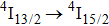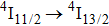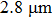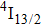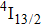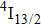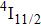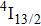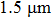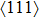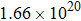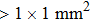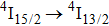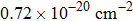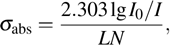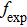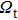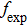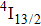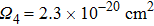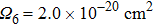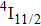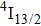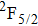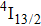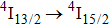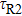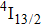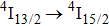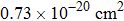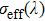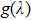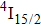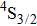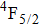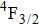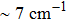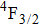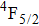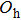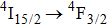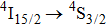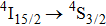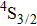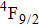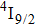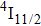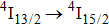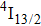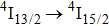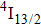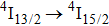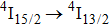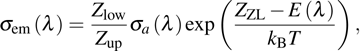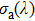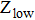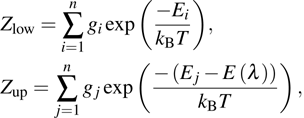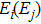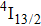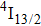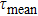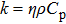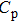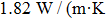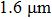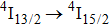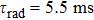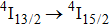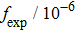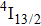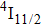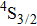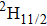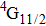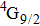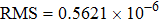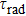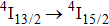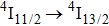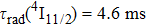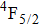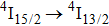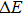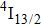1. IntroductionCalcium fluoride (CaF2) has been used as a host crystal for rare earth ions in numerous pioneer works on solid-state lasers that appeared in the early sixties of the past century. Following demonstration of the laser action in CaF2 doped with Sm2+,[1] considerable attention has been paid to spectroscopic and laser properties of trivalent rare earth ions, mainly Nd3+ ions in CaF2[2] and in a variety of mixed compounds CaF2–YF3[3] and CaF2–REF3 (RE = Ce, La, Gd).[4,5] These early works revealed that the manufacture of calcium fluoride crystals having excellent optical quality and large volume is relatively easy and not expensive. However, the problem of charge compensation occurs when they are doped with trivalent rare earth ions.
It was observed that at a very low concentration rare earth ions reside in isolated centers with cubic, tetragonal, and trigonal site symmetries differing in number and spatial arrangement of ligands. With increasing the concentration, more complex chromophoric centers consisting of dimers are created, and eventually large clusters appear when the rare earth concentration is in the range of tens of percent. In addition, it was found that the distribution of rare earth ions in different chromophoric centers depends on the radii of rare earth ions and on their concentration. In mixed compounds mentioned above, the inherent structural disorder brings about a significant inhomogeneous broadening of spectral lines, and the nature of rare earth sites is even more difficult to determine. In one of the early works, it was concluded that incorporation of YF3 to CaF2 results in the creation of new types of centers.[6] However, in a subsequent work, it was concluded that the presence of YF3 affects merely the distribution of rare earth ions over existing centers in CaF2.[7] In view of these problems, CaF2 crystals doped with trivalent rare earth ions have not been regarded as promising laser materials during several decades. In fact, fundamental spectroscopic parameters relevant to the laser performance of a CaF2:Nd system have been reported quite recently.[8]
Renewal of the interest in these systems that occurred over the course of several years is related to the search for broad-band emitting materials for the design of all-solid-state high-power ultrafast lasers. In a recent paper, advantages and drawbacks of CaF2:Yb3+ systems, denoted by authors as “a new old laser crystal,” have been revised and compared to other ytterbium-doped crystals that may be of interest for this purpose.[9] Taking into account the performance of CaF2:Yb3+ high-power and/or femtosecond lasers reported in numerous papers published during the last ten years, the authors have underlined the importance of this material for practical application.
In contrast to the knowledge of CaF2:Yb3+ on the laser potential of erbium-doped CaF2 crystals is rather poor. In several early papers, spectroscopic features[10] were reported, and the feasibility of laser action associated with the
 transition at approximately 850 nm and with the
transition at approximately 850 nm and with the
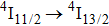 transition at approximately
transition at approximately
 at cryogenic temperatures was demonstrated.[11] Recently, a laser operation associated with the
at cryogenic temperatures was demonstrated.[11] Recently, a laser operation associated with the
 transition of Er3+ in CaF2 at approximately
transition of Er3+ in CaF2 at approximately
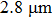 has been observed at room temperature upon optical pumping at 800 nm and 975 nm with a Ti-sapphire laser and at 1520 nm with a color center laser.[12] However, laser operation on the
has been observed at room temperature upon optical pumping at 800 nm and 975 nm with a Ti-sapphire laser and at 1520 nm with a color center laser.[12] However, laser operation on the
 transition at approximately
transition at approximately
 was a significant problem since a large energy gap between the
was a significant problem since a large energy gap between the
 level and the
level and the
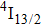 level, combined with a relatively low energy of lattice vibration of the CaF2 host, results in a small multiphonon relaxation rate thereby preventing the energy flow to the
level, combined with a relatively low energy of lattice vibration of the CaF2 host, results in a small multiphonon relaxation rate thereby preventing the energy flow to the
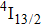 level from higher energy pump levels. As a consequence, a practically significant population inversion cannot be obtained, unless the
level from higher energy pump levels. As a consequence, a practically significant population inversion cannot be obtained, unless the
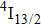 level is resonantly pumped. These findings were not encouraging. Nevertheless, a recent discovery of an efficient energy transfer process between Er3+ and Ce3+ that is able to drastically enhance the energy flow from the
level is resonantly pumped. These findings were not encouraging. Nevertheless, a recent discovery of an efficient energy transfer process between Er3+ and Ce3+ that is able to drastically enhance the energy flow from the
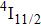 level to the
level to the
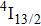 level of erbium[13] may open new means to overcome the problem. In fact, recent investigation of Yb/Er:CeF3 nanoparticles synthesized by the hydrothermal process revealed a high efficiency of
level of erbium[13] may open new means to overcome the problem. In fact, recent investigation of Yb/Er:CeF3 nanoparticles synthesized by the hydrothermal process revealed a high efficiency of
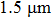 emission upon exciting at 975 nm without visible up-conversion luminescence.[14] Additionally, it was demonstrated that the rate of the
emission upon exciting at 975 nm without visible up-conversion luminescence.[14] Additionally, it was demonstrated that the rate of the
 transition in an Er/Yb/Na/Ce:CaF2 crystal was enhanced by about 40 times by the deactivating effect of Ce3+.[15]
transition in an Er/Yb/Na/Ce:CaF2 crystal was enhanced by about 40 times by the deactivating effect of Ce3+.[15]
Encouraged by the findings above, we investigate the fundamental properties of an erbium-doped CaF2–CeF3 (Ca:Ce = 2:1) disordered crystal, which are relevant to the laser performance at approximately
 . In our previous paper,[16] preliminary spectroscopic data on erbium-doped as well as erbium and ytterbium co-doped CaF2–CeF3 consisting of the Judd–Ofelt treatment, room-temperature luminescence spectra calibrated in terms of arbitrary units, and decay curves were reported. In the present work, we report a more detailed and comprehensive investigation of a CaF2–CeF3 crystal single-doped with Er3+ ions. First, the Judd–Ofelt analysis was refined considering the contribution of the magnetic dipole (MD) mechanism to both absorption and emission transitions. Next, the emission cross section and gain coefficient as functions of the wavelength for the
. In our previous paper,[16] preliminary spectroscopic data on erbium-doped as well as erbium and ytterbium co-doped CaF2–CeF3 consisting of the Judd–Ofelt treatment, room-temperature luminescence spectra calibrated in terms of arbitrary units, and decay curves were reported. In the present work, we report a more detailed and comprehensive investigation of a CaF2–CeF3 crystal single-doped with Er3+ ions. First, the Judd–Ofelt analysis was refined considering the contribution of the magnetic dipole (MD) mechanism to both absorption and emission transitions. Next, the emission cross section and gain coefficient as functions of the wavelength for the
 transition were evaluated. In subsequent sections, we present and discuss low-temperature optical spectra and results of extended x-ray-absorption fine structure (EXAFS) and thermal conductivity measurements. As far as we know, the information gathered in this work has not been reported before. The results obtained in this study are discussed with reference to the data for a CaF2:Er3+ system reported in Refs. [7] and [17].
transition were evaluated. In subsequent sections, we present and discuss low-temperature optical spectra and results of extended x-ray-absorption fine structure (EXAFS) and thermal conductivity measurements. As far as we know, the information gathered in this work has not been reported before. The results obtained in this study are discussed with reference to the data for a CaF2:Er3+ system reported in Refs. [7] and [17].
2. ExperimentalCrystal CaF2–CeF3 doped with Er3+ was grown by the temperature gradient technique (TGT) described in Ref. [18]. The raw materials (CaF2, CeF3, ErF3, and PbF2) were mixed according to the chemical ratios and put into the sealed graphite crucible. The ratio of CeF3 and CaF2 was 1:2. The PbF2 (1 mol%) powder was used as the oxygen scavenger. The mixtures were melted at 1400 °C and then grown on
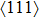 CaF2 seeds with reducing the temperature at a cooling rate of ∼ 5 °C/h. In this way, the CaF2–CeF3 transparent crystal with Er3+ was obtained. The erbium concentrations at different parts of the grown crystal were checked by the inductively coupled plasma atomic emission spectrometry analysis. It was found that the actual concentration of Er3+ in the grown crystal was significantly lower than the original one (1.4%) implying that the segregation coefficient is inferior to unity. To obtain meaningful spectroscopic data, the Er3+concentration in the part of the crystal adjacent to a sample was measured to be 1.06%, which is equivalent to
CaF2 seeds with reducing the temperature at a cooling rate of ∼ 5 °C/h. In this way, the CaF2–CeF3 transparent crystal with Er3+ was obtained. The erbium concentrations at different parts of the grown crystal were checked by the inductively coupled plasma atomic emission spectrometry analysis. It was found that the actual concentration of Er3+ in the grown crystal was significantly lower than the original one (1.4%) implying that the segregation coefficient is inferior to unity. To obtain meaningful spectroscopic data, the Er3+concentration in the part of the crystal adjacent to a sample was measured to be 1.06%, which is equivalent to
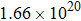 Er3+ ions per cubic centimeter.
Er3+ ions per cubic centimeter.
The absorption spectra of the crystal were recorded with a Varian Model 5E UV-visible-near-IR (UV-VIS-NIR) absorption spectrophotometer at 10 K and 300 K. The spectral bandwidth of the spectrophotometer was set to 0.1 nm in the UV-VIS region and to 0.2 nm in the NIR region. The emission spectra at 300 K and at 10 K were excited by an argon ion laser at 514 nm and recorded with the Dongwoo Optron monochromator DM 711 with a focal length of 750 mm, coupled to a cooled InGaAs infrared detector. For low-temperature measurements, the sample was put into an Oxford Model CF 1204 continuous flow liquid helium cryostat equipped with a temperature controller.
EXAFS data were obtained using a facility available in the National Synchrotron Radiation Laboratory, University of Science and Technology of China. Measurements were made at room temperature at the Er L-edge (8794 eV) and in the fluorescence mode, owing to the low contentment of erbium in the crystal, by using a Si (111) double crystal monochromator. The XAFS measurements were conducted in the nonfocused mode, and the corresponding spot diameter was
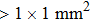 . The XAFS spectra were recorded from 8794 eV to 9933 eV, every 0.5 eV with a 5 s accumulation time per point. All the spectra were normalized in the same way using Athema[19] software.
. The XAFS spectra were recorded from 8794 eV to 9933 eV, every 0.5 eV with a 5 s accumulation time per point. All the spectra were normalized in the same way using Athema[19] software.
The thermal diffusivity of the material was measured with an LFA-427 laser flash diffusivity apparatus (NETZSC Ltd, Germany). The laser pulse intensity was 0–20 J, pulse width between 0.2 ms and 1.2 ms. For this measurement, a sample in the form of a disk 10 mm in diameter and 1.7 mm thick was prepared.
3. Results and discussion3.1. Room-temperature optical spectra and transition intensitiesA survey absorption spectrum recorded at room temperature for the CaF2–CeF3 crystal containing 1.06% of Er3+ is shown in Fig. 1. Broad unresolved spectral bands that appear in the spectrum show an inhomogeneous broadening characteristic for rare earth ions embedded in the crystal lattices with significant structural disorder.
From the room-temperature absorption spectrum, the peak absorption cross section of the Er3+
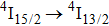 transition is calculated to be approximately
transition is calculated to be approximately
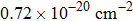 with the equation
with the equation
where
L is the thickness of the sample,
N is the concentration of the Er
3+ ions (cm
−3), and

is the absorption light density.
The transition intensities for the Er3+:CaF2–CeF3 system were analyzed within a framework of the standard Judd–Ofelt approach.[20,21] The experimental oscillator strengths
 for the absorption transitions were determined by a numerical integration of the absorption bands shown in Fig. 1. The Judd–Ofelt theory accounts for electric dipole (ED) transitions. Magnetic dipole MD transitions obey selection rules
for the absorption transitions were determined by a numerical integration of the absorption bands shown in Fig. 1. The Judd–Ofelt theory accounts for electric dipole (ED) transitions. Magnetic dipole MD transitions obey selection rules
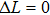 ,
,
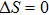 ,
,
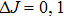 (except for
(except for
 ). Therefore, the contribution of the MD mechanism to the
). Therefore, the contribution of the MD mechanism to the
 absorption intensity was evaluated and next subtracted from the experimental oscillator strength
absorption intensity was evaluated and next subtracted from the experimental oscillator strength
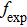 for this transition prior to the fitting procedure. To determine intensity parameters
for this transition prior to the fitting procedure. To determine intensity parameters
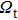 , a set of ten experimental
, a set of ten experimental
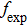 values were used as input data in the procedure of fitting the experimental and theoretical oscillator strengths by the least squares technique. The expression for theoretical oscillator strengths was constructed using the reduced matrix elements from Ref. [22]. The results of the fitting are gathered in Table 1.
values were used as input data in the procedure of fitting the experimental and theoretical oscillator strengths by the least squares technique. The expression for theoretical oscillator strengths was constructed using the reduced matrix elements from Ref. [22]. The results of the fitting are gathered in Table 1.
Table 1.
Table 1.
 | Table 1.
Experimental and theoretical oscillator strengths of Er3+ transitions in the CaF2–CeF3:Er3+ crystal.
. |
The Judd–Ofelt parameters determined during the fitting procedure were next used to evaluate the rates of ED transitions originating in the
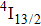 and
and
 excited states. Next, the calculated MD transition rates were added to obtain the total transition rates, corresponding radiative lifetimes, and luminescence branching ratios relevant to the laser operation of Er3+ in the CaF2–CeF3 matrix. The results of the calculation are given in Table 2.
excited states. Next, the calculated MD transition rates were added to obtain the total transition rates, corresponding radiative lifetimes, and luminescence branching ratios relevant to the laser operation of Er3+ in the CaF2–CeF3 matrix. The results of the calculation are given in Table 2.
Table 2.
Table 2.
 | Table 2.
Radiative transition probabilities A, radiative lifetimes
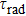 , and branching ratios of luminescence β determined for selective Er3+ transitions in the CaF2–CeF3:Er crystal.
, and branching ratios of luminescence β determined for selective Er3+ transitions in the CaF2–CeF3:Er crystal.
. |
The Judd–Ofelt parameters
 mentioned above differ slightly from those reported in Ref. [16] since in contrast to the previous calculation, the contribution of MD transition was included. The same applies to the calculated values of the radiative transition rates and radiative lifetimes gathered in Table 2.
mentioned above differ slightly from those reported in Ref. [16] since in contrast to the previous calculation, the contribution of MD transition was included. The same applies to the calculated values of the radiative transition rates and radiative lifetimes gathered in Table 2.
The comparison of the values in Tables 1 and 2 with those reported in Ref. [17] for a CaF2 crystal containing 0.1% of Er3+ reveals that the intensities of the absorption transitions in the two systems are within the same order of magnitude. However, the dissimilarity between the Judd–Ofelt parameters
 ,
,
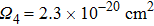 , and
, and
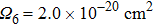 reported for CaF2:Er3+ systems and those for Er3+ in the CaF2–CeF3 matrix is significant.
reported for CaF2:Er3+ systems and those for Er3+ in the CaF2–CeF3 matrix is significant.
The energy between the
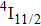 and
and
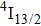 multiplets of Er3+ ions is approximately 3600 cm−1, which is almost the same as the band gap between the
multiplets of Er3+ ions is approximately 3600 cm−1, which is almost the same as the band gap between the
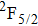 and
and
 energy level of Ce3+ ions.[16] Therefore, the decay of the
energy level of Ce3+ ions.[16] Therefore, the decay of the
 transition of Er3+ ions would be significantly improved through the resonant energy transfer from Er3+ ions and Ce3+ ions. The improvement of the decay rate corresponding to the
transition of Er3+ ions would be significantly improved through the resonant energy transfer from Er3+ ions and Ce3+ ions. The improvement of the decay rate corresponding to the
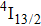 multiplet of Er3+ ions can reduce the excited state absorption and even the clusters of Er–Er ions. Figure 2 shows the details of the
multiplet of Er3+ ions can reduce the excited state absorption and even the clusters of Er–Er ions. Figure 2 shows the details of the
 absorption band and of the
absorption band and of the
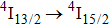 emission band recorded at room temperature. The shown emission band was calibrated in terms of the emission cross section units using the Fuchtbauer–Ladenburg relation
emission band recorded at room temperature. The shown emission band was calibrated in terms of the emission cross section units using the Fuchtbauer–Ladenburg relation
where
β is the branching ratio (for the

level,
β= 1);
n is the refraction index of the crystal, which is measured to be approximately 1.50;
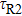
is the radiative lifetime of the
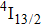
level, which is calculated to be 5.5 ms using the J–O theory; and

represents the experimental emission intensity as a function of the wavelength
λ.
It may be interesting to compare peculiarities of the
 emission presented above with those reported for a CaF2 crystal containing 0.01% of Er3+.[17] Owing to a small doping level, erbium ions in this sample are likely to enter isolated centers.[23,24] The reported
emission presented above with those reported for a CaF2 crystal containing 0.01% of Er3+.[17] Owing to a small doping level, erbium ions in this sample are likely to enter isolated centers.[23,24] The reported
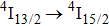 emission spectrum contains four local maxima at 1460, 1505, 1522, and 1540 nm; nevertheless, the overall width of this spectrum is nearly the same as that recorded for our CaF2–CeF3:Er3+ sample. In addition, the spectral positions of the band maximum for the two systems differ by several nanometers only. From this comparison, it follows that the diversity of transition energy values for different Er3+ centers that contribute to the broad-band emission in the CaF2–CeF3:Er3+ system is small.
emission spectrum contains four local maxima at 1460, 1505, 1522, and 1540 nm; nevertheless, the overall width of this spectrum is nearly the same as that recorded for our CaF2–CeF3:Er3+ sample. In addition, the spectral positions of the band maximum for the two systems differ by several nanometers only. From this comparison, it follows that the diversity of transition energy values for different Er3+ centers that contribute to the broad-band emission in the CaF2–CeF3:Er3+ system is small.
It can be seen from Fig. 2 that the peak emission cross section at ∼ 1544 nm is
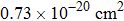 . When considering the laser potential in this spectral region, the adverse effect of the self-absorption should be accounted for. For this purpose, we follow the commonly used approach and calculate the effective emission cross section as a function of the wavelength
. When considering the laser potential in this spectral region, the adverse effect of the self-absorption should be accounted for. For this purpose, we follow the commonly used approach and calculate the effective emission cross section as a function of the wavelength
 using the relation
using the relation
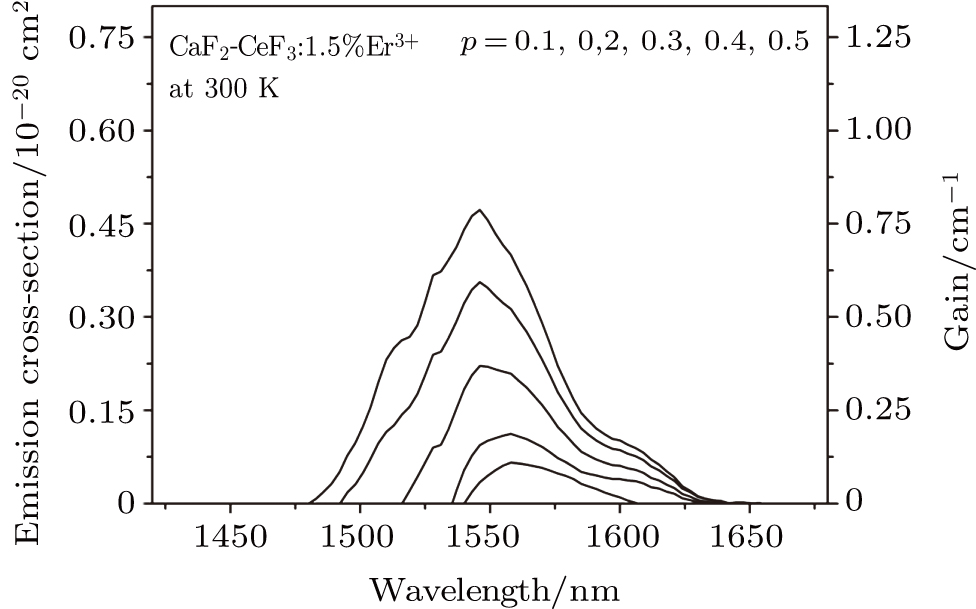
 , where p is the population inversion parameter, defined as the density of excited Er3+ ions divided by the overall erbium concentration N0. Figure 3 shows the plots of
, where p is the population inversion parameter, defined as the density of excited Er3+ ions divided by the overall erbium concentration N0. Figure 3 shows the plots of
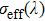 as a function of the wavelength calculated for p values ranging from 0.1 to 0.5. From these plots, it follows that the gain
as a function of the wavelength calculated for p values ranging from 0.1 to 0.5. From these plots, it follows that the gain
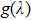 defined as
defined as
 will be positive even for the p parameter as low as 0.1. For p = 0.5, a reasonable value likely to be encountered in practice, a broad spectral range of the potential laser operation stretching from about 1480 nm to 1630 nm is predicted for the Er-doped CeF3–CaF2 disordered crystal.
will be positive even for the p parameter as low as 0.1. For p = 0.5, a reasonable value likely to be encountered in practice, a broad spectral range of the potential laser operation stretching from about 1480 nm to 1630 nm is predicted for the Er-doped CeF3–CaF2 disordered crystal.
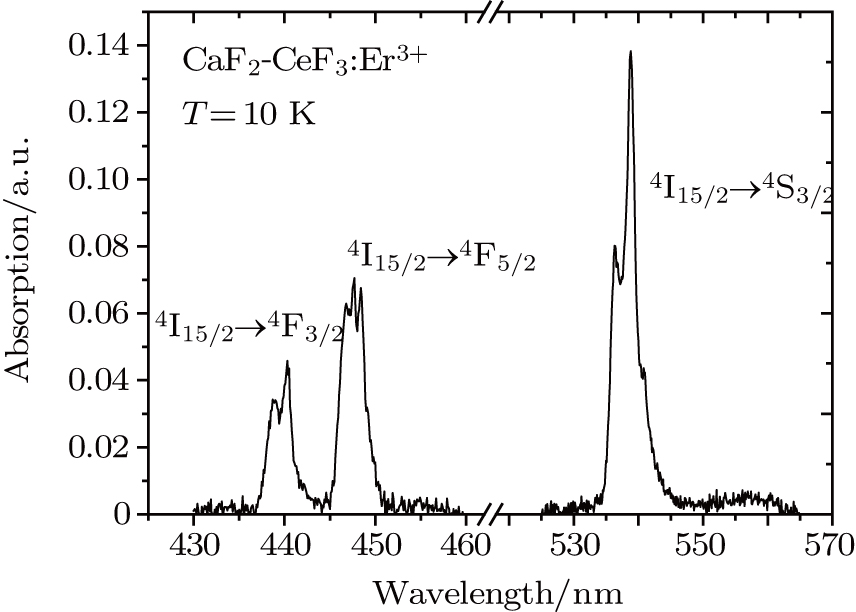
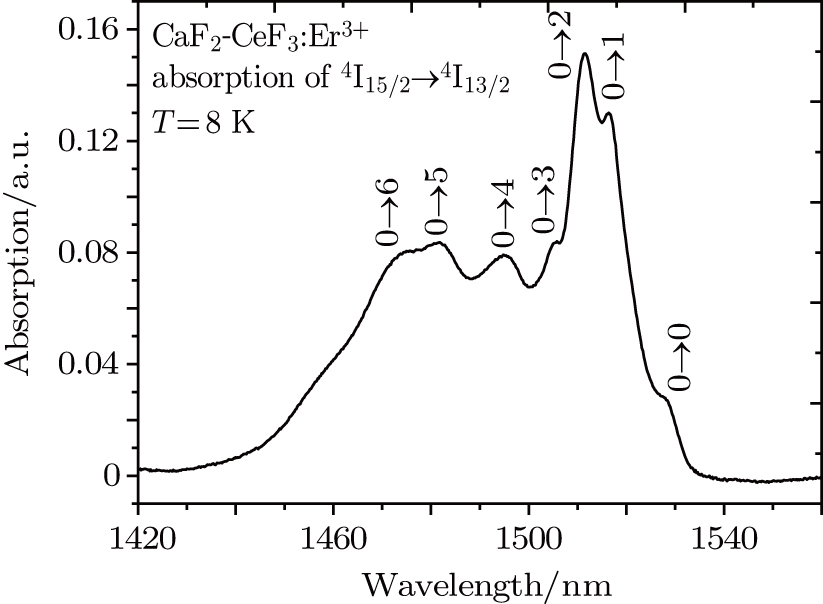
3.2. Nature of Er3+ sites in the CaF2–CeF3 matrixThe above-described analysis of the transition intensities and the calibration of the absorption and emission bands were performed for broad unresolved optical spectra that contain, in principle, contributions from all different Er3+ centers, whatever their number and types are. However, when considering the laser potential of such a disordered material, the question whether among numerous Er3+ centers a dominant one exists is of crucial importance. An outstanding laser potential of a CaF2 crystal heavily doped with Yb3+ stems from the fact that almost all ytterbium ions reside in only one kind of center (hexameric type) rather than in various isolated and dimer centers that are encountered when the Yb3+ concentration is small.[25–28] To get a closer insight into the nature of Er3+ sites in the CaF2–CeF3 matrix, optical spectra were recorded at a low temperature and examined carefully. Figure 4 shows the details of the absorption bands related to the transitions from the ground
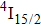 multiplet to the excited
multiplet to the excited
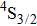 ,
,
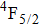 , and
, and
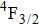 multiplets recorded at 10 K.
multiplets recorded at 10 K.
At T = 10 K, the kT value is
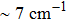 . Thus, one can expect that the lowest crystal field component of the ground
. Thus, one can expect that the lowest crystal field component of the ground
 multiplet solely will have a population high enough to contribute to the absorption transitions. For each particular Er3+ center, two crystal field components of the
multiplet solely will have a population high enough to contribute to the absorption transitions. For each particular Er3+ center, two crystal field components of the
 and
and
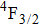 multiplets and three crystal field components of the
multiplets and three crystal field components of the
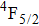 multiplet are predicted (neglecting isolated centers with
multiplet are predicted (neglecting isolated centers with
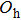 symmetry). It can be seen in Fig. 4 that the band related to the
symmetry). It can be seen in Fig. 4 that the band related to the
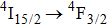 transition contains two components peaking at 437 nm and 440 nm, and the band related to the
transition contains two components peaking at 437 nm and 440 nm, and the band related to the
 transition contains three components peaking at 447, 448, and 449 nm. In the band related to the
transition contains three components peaking at 447, 448, and 449 nm. In the band related to the
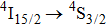 transition, two intense components peaking at 536 nm and 539 nm are clearly seen, and a weaker third component at 541 nm can be discerned. Although the number of band components in these spectra complies with the number of crystal field components of the terminal multiplets, the overall spectral widths of the bands is large (between 5 nm and 10 nm) indicating that we observe the superposition of numerous transitions having slightly different energy. There is a striking similarity between the low-temperature spectra shown above and the corresponding absorption spectra at 77 K for the CaF2 crystal containing 1% of Er3+ and for the CaF2 crystal containing Er3+ and YF3 with a concentration up to 2% reported in Ref. [7]. This early study revealed that for an Er3+ concentration of 0.01%, absorption spectra related to the
transition, two intense components peaking at 536 nm and 539 nm are clearly seen, and a weaker third component at 541 nm can be discerned. Although the number of band components in these spectra complies with the number of crystal field components of the terminal multiplets, the overall spectral widths of the bands is large (between 5 nm and 10 nm) indicating that we observe the superposition of numerous transitions having slightly different energy. There is a striking similarity between the low-temperature spectra shown above and the corresponding absorption spectra at 77 K for the CaF2 crystal containing 1% of Er3+ and for the CaF2 crystal containing Er3+ and YF3 with a concentration up to 2% reported in Ref. [7]. This early study revealed that for an Er3+ concentration of 0.01%, absorption spectra related to the
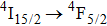 and
and
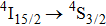 transitions consist of several very narrow lines, but when the Er3+ concentration increased to 1%, the intensity of narrow lines disappeared almost completely in favor of new broad bands, each of them having the overall spectral width of about 2 nm and two local maxima. Similar spectra were observed for the CaF2 crystal containing a much smaller content of Er3+, but containing an admixture of YF3, and this finding led to the conclusion that the spectra are affected by the sum of the ErF3 and YF3 concentrations rather than the Er3+ concentration alone. In our crystal, the sum of the CeF3 and ErF3 concentrations is considerably higher than that in the system mentioned above. Resulting structural disorder induces strong inhomogeneous broadening of absorption bands, but weakly affects the spectral positions of the band maxima. Figure 5 shows the absorption spectrum related to the
transitions consist of several very narrow lines, but when the Er3+ concentration increased to 1%, the intensity of narrow lines disappeared almost completely in favor of new broad bands, each of them having the overall spectral width of about 2 nm and two local maxima. Similar spectra were observed for the CaF2 crystal containing a much smaller content of Er3+, but containing an admixture of YF3, and this finding led to the conclusion that the spectra are affected by the sum of the ErF3 and YF3 concentrations rather than the Er3+ concentration alone. In our crystal, the sum of the CeF3 and ErF3 concentrations is considerably higher than that in the system mentioned above. Resulting structural disorder induces strong inhomogeneous broadening of absorption bands, but weakly affects the spectral positions of the band maxima. Figure 5 shows the absorption spectrum related to the
 transition of Er3+in the CaF2–CeF3 crystal recorded at 8 K. After the Gaussian fitting process, it was found that the band consists of seven components (as shown in Fig. 5). The crystal field splitting of the Er3+
transition of Er3+in the CaF2–CeF3 crystal recorded at 8 K. After the Gaussian fitting process, it was found that the band consists of seven components (as shown in Fig. 5). The crystal field splitting of the Er3+
 manifold was determined from this spectrum.
manifold was determined from this spectrum.
Valuable information regarding the nature of rare earth sites in crystal hosts can be obtained usually from low-temperature luminescence spectra. Unfortunately, attempts to record spectra of luminescence originating in the
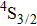 ,
,
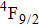 ,
,
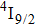 , and
, and
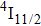 levels of Er3+ in our crystal both at room temperature and at 10 K were unsuccessful because emission from the levels higher than
levels of Er3+ in our crystal both at room temperature and at 10 K were unsuccessful because emission from the levels higher than
 is completely quenched by Ce3+ ions. Figure 6 shows the low-temperature spectrum related to the
is completely quenched by Ce3+ ions. Figure 6 shows the low-temperature spectrum related to the
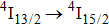 transition of Er3+ in the CaF2–CeF3 matrix. An argon ion laser emitting at 514 nm was used as an excitation source, and the spectral resolution of an emission monochromator used was set to 0.1 nm. Assignment of the band components indicated in the figure was made by Gaussian fitting with reference to the crystal field splitting of the
transition of Er3+ in the CaF2–CeF3 matrix. An argon ion laser emitting at 514 nm was used as an excitation source, and the spectral resolution of an emission monochromator used was set to 0.1 nm. Assignment of the band components indicated in the figure was made by Gaussian fitting with reference to the crystal field splitting of the
 multiplet mentioned above. Some comments are needed to account for an assignment of the band component on the high-energy side of the spectrum to transitions originating from the second and third crystal field levels of the
multiplet mentioned above. Some comments are needed to account for an assignment of the band component on the high-energy side of the spectrum to transitions originating from the second and third crystal field levels of the
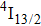 multiplet. If the temperature of the excited region of the crystal sample amounted actually to 10 K, these transitions should be negligibly weak. However, in contrast to the absorption spectra measurement, the power dissipated in a small region of the sample excited with a focused laser beam may result in a local increase in the sample temperature, especially when the thermal conductivity of the crystal is small (vide infra).
multiplet. If the temperature of the excited region of the crystal sample amounted actually to 10 K, these transitions should be negligibly weak. However, in contrast to the absorption spectra measurement, the power dissipated in a small region of the sample excited with a focused laser beam may result in a local increase in the sample temperature, especially when the thermal conductivity of the crystal is small (vide infra).
Table 3 summarizes the energies of the crystal field levels for the
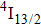 and
and
 multiplets of Er3+ ions in the CaF2–CeF3 crystal as determined from the low-temperature absorption and emission spectra. To check the reliability of the data in Table 3 above, we evaluated the room-temperature
multiplets of Er3+ ions in the CaF2–CeF3 crystal as determined from the low-temperature absorption and emission spectra. To check the reliability of the data in Table 3 above, we evaluated the room-temperature
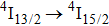 emission band by the so-called reciprocity method that relays on the measured
emission band by the so-called reciprocity method that relays on the measured
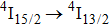 absorption spectrum according to the relation
absorption spectrum according to the relation
where
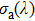
is the absorption cross section and
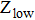
and

are the partition functions for the lower and upper states, respectively, defined as
where

are the degeneracies of the crystal field levels,
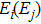
are the energies of the crystal field levels,

is the energy separation between the lowest crystal field levels of the upper and lower states, and

is the Boltzmann constant.
Table 3.
Table 3.
 | Table 3.
Energies of the crystal field levels (in cm−1) of Er3+ ions in the CaF2–CeF3 disordered crystal.
. |
Figure 7 compares the spectra obtained by the reciprocity method defined above and by the Fuchtbauer–Ladenburg method described in the previous section. It can be seen in this figure that the agreement between the spectra is surprisingly good. The results presented above seem to indicate that in spite of the structural disorder, a majority of erbium ions reside in one kind of site, an analogue of hexomeric sites reported for a CaF2 crystal heavily doped with Yb3+ ions. However, the recorded decay curve of the
 emission does not corroborate this supposition.
emission does not corroborate this supposition.
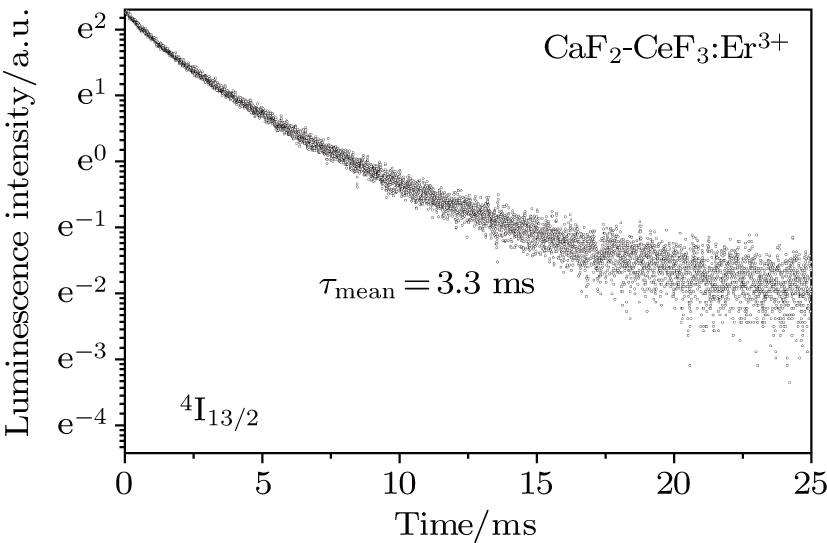
Figure 8 shows the semilog plot of the
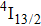 luminescence decay curve recorded at room temperature. It can be seen that in the whole time scale the curve is far from a single exponential time dependence implying that erbium ions having markedly different relaxation rates contribute to the luminescence. As a consequence, the definitive
luminescence decay curve recorded at room temperature. It can be seen that in the whole time scale the curve is far from a single exponential time dependence implying that erbium ions having markedly different relaxation rates contribute to the luminescence. As a consequence, the definitive
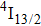 lifetime cannot be determined from this decay curve, and the so-called mean lifetime
lifetime cannot be determined from this decay curve, and the so-called mean lifetime
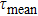 defined by the relation
defined by the relation
in which
I is the intensity of luminescence and
t represents time, can be found solely. In this way,

was calculated. The mean lifetime defined above takes into account the contribution of a slower decay in the tail of the decay curve. Thus, its value is slightly higher than the lifetime value of 2.99 ms reported in Ref. [
16].
An attempt was made to obtain more information from the EXAFS measurement. Figure 9 shows the EXAFS spectra for the Er3+:CaF2–CeF3 disordered crystal. Some structural information on the doped ions in the crystal can be obtained by fitting the Fourier transform for the experimental data. It was found that the average coordination number of Er3+ ions in the grown crystal is 9.8, which is higher than that in Er3+-CaF2:8 or 9 at 2.3–2.4 Å,[29] and the average length of [Er–F] bonds is approximately 2.6 Å.
3.3. Thermal conductivityThe thermal diffusion coefficient η of our sample was measured to be 0.00444 cm2/s. From this value, the thermal conductivity k was calculated using the equation
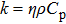 , where k, η, ρ, and
, where k, η, ρ, and
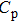 denote the thermal conductivity, thermal diffusion coefficient, density, and the specific heat of the crystal, respectively. By inserting the values of ρ = 4.8 g/cm3 and
denote the thermal conductivity, thermal diffusion coefficient, density, and the specific heat of the crystal, respectively. By inserting the values of ρ = 4.8 g/cm3 and
 to the equation above, the thermal conductivity of the crystal was calculated to be
to the equation above, the thermal conductivity of the crystal was calculated to be
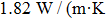 ). The obtained value of the thermal conductivity is small. The thermal conductivity of the undoped CaF2 single crystal was measured to be
). The obtained value of the thermal conductivity is small. The thermal conductivity of the undoped CaF2 single crystal was measured to be
 ).[30] Upon doping with rare earth ions, the thermal conductivity decreases because incorporated ions act as point defects affecting adversely the mean free path of phonons. For the CaF2 crystal heavily doped with Yb3+ (2.59 %), it amounts to 5.4 W/(mK).[9] In spite of a smaller Er3+ concentration, the degree of disorder in the CaF2–CeF3 crystal is markedly higher, and therefore its thermal conductivity is poor. The thermal properties can be improved by the optimization of the doping concentration, and in general, the Er3+:CaF2–CeF3 disordered crystal is a promising candidate for broad-band laser operation from 1480 nm to 1630 nm.
).[30] Upon doping with rare earth ions, the thermal conductivity decreases because incorporated ions act as point defects affecting adversely the mean free path of phonons. For the CaF2 crystal heavily doped with Yb3+ (2.59 %), it amounts to 5.4 W/(mK).[9] In spite of a smaller Er3+ concentration, the degree of disorder in the CaF2–CeF3 crystal is markedly higher, and therefore its thermal conductivity is poor. The thermal properties can be improved by the optimization of the doping concentration, and in general, the Er3+:CaF2–CeF3 disordered crystal is a promising candidate for broad-band laser operation from 1480 nm to 1630 nm.