Cite this Article
Hu Xiaoyu, Liu Chongxin, Liu Ling, Yao Yapeng, Zheng Guangchao. Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system. Chinese Physics B, 2017, 26(11): 110502  
Permissions
Multi-scroll hidden attractors and multi-wing hidden attractors in a 5-dimensional memristive system
Hu Xiaoyu †, Liu Chongxin, Liu Ling, Yao Yapeng, Zheng Guangchao
State Key Laboratory of Electrical Insulation and Power Equipment, School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China

 

† Corresponding author. E-mail: huxiaoyucool@163.com

Abstract

A novel 5-dimensional (5D) memristive chaotic system is proposed, in which multi-scroll hidden attractors and multi-wing hidden attractors can be observed on different phase planes. The dynamical system has multiple lines of equilibria or no equilibrium when the system parameters are appropriately selected, and the multi-scroll hidden attractors and multi-wing hidden attractors have nothing to do with the system equilibria. Particularly, the numbers of multi-scroll hidden attractors and multi-wing hidden attractors are sensitive to the transient simulation time and the initial values. Dynamical properties of the system, such as phase plane, time series, frequency spectra, Lyapunov exponent, and Poincaré map, are studied in detail. In addition, a state feedback controller is designed to select multiple hidden attractors within a long enough simulation time. Finally, an electronic circuit is realized in Pspice, and the experimental results are in agreement with the numerical ones.

PACS: 05.45.-a;05.45.Jn;05.45.Pq
Keyword:multi-scroll hidden attractors;multi-wing hidden attractors;multiple lines equilibria;no equilibrium
1. Introduction

It is confirmed that dynamical systems with multi-scroll attractors or multi-wing attractors carry much more complexity than those with fewer attractors, and they have been widely used in some areas, such as image encryption,[1] secure communication,[2,3] and chaotic cryptanalysis.[4] Therefore, during the last few decades the dynamical systems with multi-scroll attractors or multi-wing attractors have attracted a great deal of attention from researchers.[5–7] Meanwhile, various nonlinear control schemes which are based on nonlinear functions are proposed to generate multi-scroll attractors or multi-wing attractors, such as hyperbolic function,[8] trigonometric function,[9,10] and switching controller.[11,12] In addition, the study on realization of multi-scroll attractors or multi-wing attractors makes them observable in analog circuits.[13–16] Particularly, in some fractional order systems,[17,18] and memristor-based systems,[19–22] multi-scroll attractors or multi-wing attractors can also be obtained.

The hidden attractor[23–25] is a hot topic and has attracted lots of interest recently. From a computational point of view, attractors in a chaotic system can be classified as self-excited and hidden attractors. An attractor is called a self-excited attractor if its attraction basin intersects with any neighborhoods of a stationary state (an equilibrium); otherwise, it is called a hidden attractor. The hidden attractors exist in some special dynamical systems, including ones with one stable equilibrium,[26,27] or without equilibrium,[28,29] or with a line equilibrium (infinite equilibria).[30] It is thought that the number of multi-scroll attractors or multi-wing attractors in the dynamical systems has a close relation with the system equilibria, and the dynamical systems with multi-scroll attractors or multi-wing attractors are commonly constructed by extending saddle-focus equilibrium points with index 2. However, for the systems with multi-scroll hidden attractors or multi-wing hidden attractors, the generating mechanism does not make sense because the systems have no equilibrium.

Most of the dynamical systems with hidden attractors only have one or two attractors, and the dynamical systems with multi-scroll hidden attractors or multi-wing hidden attractors are seldom reported.[31–34] In Ref. [31], Tahir et al. constructed a 4D chaotic system which has no equilibrium by applying a state feedback controller to a Lorenz-like system, and the new system has multi-wing hidden attractors. Zhou et al.[32] proposed no equilibrium hyperchaotic multi-wing attractors via introducing a memristor into a multi-wing chaotic system. Moreover, multi-scroll hidden attractors were also observed in an improved Sprott A system.[33,34] Inspired by the above references, we wonder are there some dynamical systems that can present both multi-scroll hidden attractors and multi-wing hidden attractors simultaneously? The answer is yes. In this paper, we propose a novel 5D memristive chaotic system. Compared with the systems in the references,[31–34] the novel chaotic system can present either multi-scroll hidden attractors or multi-wing hidden attractors on different phase planes. As the novel chaotic system has no equilibrium, the number of multi-scroll hidden attractors and multi-wing hidden attractors has nothing to do with the system equilibrium. Particularly, it is sensitive to the transient simulation time and initial values.

The organization of this paper is as follows. In Section 2, the mathematical model is introduced, and some dynamics analysis is carried out in a numerical way. In Section 3, an electronic circuit implementation for the new chaotic system is discussed and analyzed carefully. Section 4 summarizes this paper.

2. Mathematical model and dynamics analysis
2.1. Mathematical model

The memristor is a two-terminal electronic element which was predicted by Chua,[35] and it is also recognized as the fourth fundamental electronic element. For a memristor, the magnetic flux φ between the terminals is a function of the electric charge q that passes through the device. In this paper, a flux controlled one is used, and the nonlinear relation between terminal voltage u and terminal current i is defined as follows:

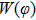
where is an incremental memductance function, and is given by

In this paper, we propose a novel dynamical system whose dynamics is described as follows:

where a, b, c, d, e, k, g, h are system parameters. The equilibria of Eq. (3) can be obtained by calculating the following equations:

The parameter k is the key factor that determines the type of solutions.

Case A: when k = 0, the equilibria of Eq. (3) are , 0, 0, 0, , where n is an integer number and is an arbitrary real constant, which means the equilibria are multiple lines equilibria.

Case B: when , obviously, there is no solution for Eq. (4) whatever the system parameters are.

According to the definition of hidden attractors, the attractors of the dynamical system under the condition of either case A or case B are hidden. In this work, we focus on the dynamical system under the condition of case B, and the system parameters are chosen as a = 0.25, b = 0.4, c = 2, d = 0.5, e = 0.5, g = 15, h = 0.01, and k = 0.05. Dynamics analyses of the new system are presented in the next subsection.

2.2. Dynamics analysis

Obviously, in case B, the new dynamical system has no equilibrium, and any attractors of this system are hidden according to the definition of hidden attractors. When the initial values and transient simulation time t = 3000 are selected, the numerical results are shown in Fig. 1. In Fig. 1, 4-scroll hidden attractors and 8 butterfly wing hidden attractors can be observed on the x–y phase plane and y–u phase plane, respectively. The projections on different phase planes show the clear characteristic that all the hidden attractors are solid, which are different from the self-excited attractors.

Figure 1. (color online) Hidden attractors of system (3) with initial values , and transient simulation time t = 3000 time units: (a) 4 scrolls hidden attractors on the x–y phase plane, (b) 8 butterfly wing hidden attractors on the y–u phase plane.

According to the chaos theory, Lyapunov exponents measure the exponential rates of divergence or convergence of nearby trajectories of a nonlinear dynamical system in phase space, and one positive Lyapunov exponent indicates that the dynamical system is chaotic. Convergence curves of four largest Lyapunov exponents of system (3) are shown in Fig. 2(a), as the time goes to 3000 time units, there always exists a positive Lyapunov exponent. Frequency spectral state variable x is shown in Fig. 2(b); its spectrum is continuous. Poincaré maps are shown in Fig. 3. The Poincaré map consists of a mess of points on the phase plane. All of the evidence indicates that the system has chaotic characteristics.

Figure 2. (color online) Dynamical properties of system (3) with initial values , and transient simulation time t = 3000 time units: (a) convergence curves of four largest Lyapunov exponents, (b) frequency spectra.
Figure 3. (color online) Poincare maps of system (3) with initial values , and transient simulation time t = 3000 time units: (a) Poincare map on the x–y phase plane with z = 0; (b) Poincare map on the y–u phase plane with x = 0.
2.3. Dynamics dependent on transient simulation time

Extensive numerical simulations confirm that the number of multi-scroll hidden attractors and multi-butterfly wing hidden attractors of the dynamical system is dependent on the transient simulation time. When the initial values are selected as , the results of the numerical simulations with different transient times are shown in Fig. 4. As shown in Fig. 4, longer transient simulation time leads to a larger number of multi-scroll or multi- butterfly wing hidden attractors.

Figure 4. (color online) Multi-scroll hidden attractors and multi-butterfly wing hidden attractors obtained by setting different transient simulation times on different phase planes, and the initial values are selected as : (a), (b) t = 300; (c), (d) t = 1000; (e), (f) t = 5000.

The dynamical system generates a different number of multi-scroll hidden attractors and multi-butterfly wing hidden attractors when the transient simulation time changes; this is because the nonlinearity of Eq. (3) is unbound,[10] which is due to the existence of the sine function in Eq. (3). Time series of state variable x are shown in Fig. 5, it is clear that the time series are non-periodic, and the absolute value of state variable x increases as the transient simulation time goes to 8000 time units, which results in a larger number of multi-scroll hidden attractors.

Figure 5. (color online) Time series of state variable x with initial values and transient simulation time selected as and t = 8000 time units.

It is inconvenient to apply this kind of attractor in reality; therefore some schemes should be employed to constrain the nonlinearity of the dynamical system. In Refs. [10] and [33], piecewise sine functions were used to avoid the augment of attractors when the transient simulation time went to infinity. Li et al.[13] handled the problem through synchronizing two systems and obtained the desired number of attractors. In Ref. [14], Ma et al. proposed a simple state feedback controller to constrain the range of state variable x, and the number of multi-scroll attractors could be selected by adjusting two control parameters. In this paper, a state feedback controller which is similar to Ref. [14] is used, and the controlled dynamical system can be rewritten as

where , α and β are the control parameters, , and is the sign function defined as follows:

When the initial values and transient simulation time t = 3000 time units are selected, the uncontrolled system (3) presents 7 scroll hidden attractors and 14 butterfly wing hidden attractors, as shown in Figs. 4(e) and 4(f), respectively. By using the same parameters and setting control parameters α = −2 and β = 8, the numerical simulation results of controlled system (5) are obtained and shown in Fig. 6. In Fig. 6(a), there are 5 scroll hidden attractors on the x–y phase plane, and the value of state variable x is limited in the range (α, β), i.e., (−2, 8). In Fig. 6(b), 10 butterfly wings are obtained on the y–u phase plane. The designed state feedback controller is simple and feasible, and the number of hidden attractors of the dynamical system can be adjusted by only controlling the two parameters.

Figure 6. (color online) Multi-scroll hidden attractors and multi-butterfly wing hidden attractors of the controlled system, the transient simulation time and initial values are selected as t = 5000 and , and the control parameters are chosen as α = −2 and β = 8: (a) 5 scroll hidden attractors on the x–y phase plane, (b) 10 butterfly wing hidden attractors on the y–u phase plane.
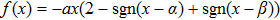
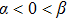
2.4. Dynamics dependent on initial values

As is known to all, the sensitivity to the initial values is a basic characteristic of chaotic systems. Particularly, it is common that the dynamical systems with hidden attractors have the feature of multistability.[36–38] In this subsection, the effects of the initial values on the dynamics of system (3) are studied. Transient simulation time is selected as t = 4000 time units, and the numerical simulation results of the dynamical system with different initial values are shown in Fig. 6.

In Figs. 7(a) and 7(b), the initial values of the numerical simulations are chosen as and , respectively, and 5 scroll hidden attractors can be observed on the x–y phase plane and the x–u phase plane. In Fig. 7(c), the initial values are selected, and 7 scroll hidden attractors are obtained on the x–y phase plane and x–u phase plane.

Figure 7. (color online) Multi-scroll hidden attractors of dynamical system (3) obtained by setting different initial values, and transient simulation time t = 4000 time units: (a), (b) ; (c), (d) ; (e), (f) .

In conclusion, besides transient simulation time, the initial values can also affect the dynamics of the system. This dynamical system has the feature of multistability, and multiple hidden attractors coexist on the same phase plane.

3. Electronic circuit implementation

Circuit implementation is a vital procedure for practical applications in reality, and it is also a feasible way to verify the corrections of numerical simulations and theory analysis. Some fundamental analog devices are used in the realization of controlled dynamical system (5), and the whole circuit diagram is shown in Fig. 8. In Fig. 8, OP-07 is used as an operational amplifier, which has saturated voltage , and the power supplies for the active device are .

Figure 8. (color online) Whole circuit implementation of system (5) in Pspice.

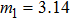
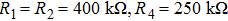
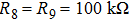
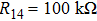
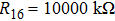
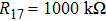
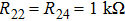
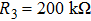
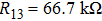
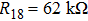
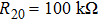
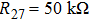
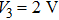
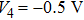
Based on the mathematical model of system (5), by applying the Kirchhoff circuit laws to the circuit in Fig. 8, the circuit equations can be written as follows:

where state variables X, Y, Z, and U are associated with the voltages across the capacitorsC1, C2, C3, and C4, respectively. State variable φ is associated with the magnetic flux obtained from the output terminal of U5. m1 is the gain module, and . , , , , , , , , , , , , , and . The balance resistors used in the circuit are selected as , , , , , , and . The voltage sources and .

The state feedback controller in system (5) is realized based on the saturated characteristic of operational amplifier OP-07. The circuit of the controller consists of operational amplifiers U7, U8, U9, U10, voltage sources V1, V2, V3, and some accessory circuit elements. The voltage sources V1 and V2 are associated with control parameters α and β. By adjusting the voltage sources V1 and V2, the desired number of multi-scroll hidden attractors and multi-butterfly wing hidden attractors can be obtained from the circuit. When the voltage sources V1 and V2 are set as and , 5 scroll hidden attractors on the x–y phase plane and 10 butterfly wing hidden attractors on the y–u phase plane can be observed, as shown in Figs. 9 and 10, respectively.

Figure 9. (color online) 5 scroll hidden attractors of system (5) on the x–y phase plane obtained by setting voltage sources and , i.e., α = −2 and β = 8.
Figure 10. (color online) 10 butterfly wing hidden attractors of system (5) on the y–u phase plane obtained by setting voltage sources and , i.e., α = −2 and β = 8.
4. Conclusion

A novel 5D chaotic system is proposed, which has no equilibrium or multiple lines equilibria. When certain system parameters are chosen, multi-scroll hidden attractors and multi-butterfly wing hidden attractors can be observed on different phase planes, and the number of multi-scroll hidden attractors and multi-butterfly wing hidden attractors has nothing to do with the system equilibrium. Extensive numerical simulations confirm that both transient simulation time and initial values have a significant impact on the number of hidden attractors. A state feedback controller is designed and added to the first equation of system (3). The unbound nonlinearity of the dynamical system can be controlled, and state variable x is limited into a desired range. By adjusting only two parameters of the controller, one can obtain the desire number of hidden attractors. The initial values can change the number and position of hidden attractors in phase space, and the effects of the initial values on the dynamics result in multiple hidden attractors coexisting in phase space.

A circuit is designed and implemented in Pspice based on the mathematical model of system (5), from which multi-scroll hidden attractors and multi-butterfly wing hidden attractors can be observed. The results of the circuit experiment have a good agreement with the numerical ones, which validates the circuit. The high complexity and adjustability of multi-scroll hidden attractors and multi-butterfly wing hidden attractors provide a good prospect for chaos-based applications, and the application of this kind of dynamical system will be studied in the near future.

Reference
[1] Han F Hu J Yu X Wang Y 2007 Appl. Math. Comput. 185 931
[2] Gámez-Guzmán L Cruz-Hernández C López-Gutiérrez R M García-Guerrero E E 2009 Commun. Nonlinear Sci. Numer. Simul. 14 2765
[3] Ben Slimane N Bouallegue K Machhout M 2017 Nonlinear Dyn.
[4] Orue A B Alvarez G Pastor G Romera M Montoya F Li S 2010 Commun. Nonlinear Sci. Numer. Simul. 15 3471
[5] Yu S Lü J Chen G 2007 Phys. Lett. 364 244
[6] Dadras S Momeni H R 2009 Phys. Lett. 373 3637
[7] Bao B Wang X Xu J 2010 2010 International Works hop on Chaos-Fractals Theories and Applications (IWCFTA) 211
[8] Xu F Yu P 2010 Journal of Mathematical Analysis & Applications 362 252
[9] Tahir F R Ali R S Pham V T Buscarino A Frasca M Fortuna L 2016 Nonlinear Dyn. 85 2665
[10] Tang W K S Zhong G Q Chen G Man K F 2001 IEEE Transactions on Circuits & Systems I: Fundamental Theory & Applications 48 1369
[11] Zhang C Yu S 2010 Phys. Lett. 374 3029
[12] Yu S Lu J Chen G Yu X 2011 IEEE Transactions on Circuits & Systems II: Express Briefs 58 314
[13] Li F Yao C 2016 Nonlinear Dyn. 84 2305
[14] Ma J Wu X Chu R Zhang L 2014 Nonlinear Dyn. 76 1951
[15] Yalçin M E 2007 Chaos Soliton. Fract. 34 1659
[16] Bao B Zhou G Xu J Liu Z 2010 Int. J. Bifurcation Chaos 20 2203
[17] Ahmad W M 2005 Chaos Soliton Fract. 25 727
[18] Deng W Lü J 2007 Phys. Lett. 369 438
[19] Cang S Wu A Wang Z Xue W Chen Z 2015 Nonlinear Dyn. 83 1987
[20] Zhou L Wang C Zhou L 2016 Nonlinear Dyn. 85 2653
[21] Wang C Xia H Zhou L 2017 Int. J. Bifurcation Chaos 27 1750091
[22] Zhou L Wang C Zhou L 2017 Int. J. Bifurcation Chaos 27 1750027
[23] Dudkowski D Jafari S Kapitaniak T Kuznetsov N V Leonov G A Prasad A 2016 Phys. Rep. 637 1
[24] Leonov G A Kuznetsov N V 2013 Int. J. Bifurcation Chaos 23 1330002
[25] Kuznetsov N V 2016 AETA 2015: Recent Advances in Electrical Engineering and Related Sciences 371 13
[26] Wang X Chen G 2012 Commun. Nonlinear Sci. Numer. Simul. 17 1264
[27] Molaie M Jafari S Sprott J C Golpayegani S M R H 2013 Int. J. Bifurcation Chaos 23 1350188
[28] Wei Z 2011 Phys. Lett. 376 102
[29] Jafari S Sprott J C Hashemi Golpayegani S M R 2013 Phys. Lett. 377 699
[30] Jafari S Sprott J C 2013 Chaos Soliton Fract. 57 79
[31] Tahir F R Jafari S Pham V T Volos C Wang X 2015 Int. J. Bifurcation Chaos 25 1550056
[32] Zhou L Wang C Zhou L 2017 Int. J. Circuit Theory Appl.
[33] Hu X Liu C Liu L Ni J Li S 2016 Nonlinear Dyn. 86 1725
[34] Jafari S Pham V T Kapitaniak T 2016 Int. J. Bifurcation Chaos 26 1650031
[35] Chua L 1971 IEEE Trans. Circuit Theory 18 507
[36] Li C Sprott J C 2014 Int. J. Bifurcation Chaos 24 1450131
[37] Li C Sprott J C 2014 Int. J. Bifurcation Chaos 24 1450034
[38] Sharma P R Shrimali M D Prasad A Kuznetsov N V Leonov G A 2015 The European Physical Journal Special Topics 224 1485