Cite this Article
Parvin F, Naqib S H. Elastic, thermodynamic, electronic, and optical properties of recently discovered superconducting transition metal boride NbRuB: An ab-initio investigation. Chinese Physics B, 2017, 26(10): 106201  
Permissions
Elastic, thermodynamic, electronic, and optical properties of recently discovered superconducting transition metal boride NbRuB: An ab-initio investigation
Parvin F, Naqib S H †
Department of Physics, University of Rajshahi, Rajshahi 6205, Bangladesh

 

† Corresponding author. E-mail: salehnaqib@yahoo.com

Abstract

The elastic, thermodynamic, electronic, and optical properties of recently discovered and potentially technologically important transition metal boride NbRuB, are investigated using the density functional formalism. Both generalized gradient approximation (GGA) and local density approximation (LDA) are used for optimizing the geometry and for estimating various elastic moduli and constants. The optical properties of NbRuB are studied for the first time with different photon polarizations. The frequency (energy) dependence of various optical constants complement quite well the essential features of the electronic band structure calculations. Debye temperature of NbRuB is estimated from the thermodynamical study. All these theoretical estimates are compared with published results, where available, and discussed in detail. Both electronic band structure and optical conductivity reveal robust metallic characteristics. The NbRuB possesses significant elastic anisotropy. Electronic features, on the other hand, are almost isotropic in nature. The effects of electronic band structure and Debye temperature on the emergence of superconductivity are also analyzed.

PACS: 62.20.Qp;71.20.Be;71.15.Mb;74.20.Pq
Keyword:hard materials;ternary borides;DFT calculations;electronic band structure;optical properties;superconductivity
1. Introduction

Ternary and binary borides (e.g., diborides) belong to a remarkable class of material mainly because of their variety of attractive physical properties suitable for diverse fields of industrial applications. One of the common features of these transition metal borides is their high values of hardness.[1–4] Hard, superhard, and ultrahard materials largely belong to the oxides, borides, nitrides, carbides of metals. In addition non-metallic cermets, carbon nitrides, cubic boron nitrides (c-BN) are also widely used.[1] For large-scale industrial applications as hard materials, high value of hardness, high incompressibility, and chemical inertness are the main requirements.

Transition metal borides are particularly interesting systems for scientific study because, in addition to hardness, they show a variety of interesting electronic ground states, including superconductivity and magnetic order.[5] One of the most prominent examples is Nd2Fe14B — the hardest of all the ferromagnetic compounds.[6] Almost all of the metallic borides show high levels of hardness and particularly the binary diborides like RuB2 and OsB2 are considered to be superhard and ultra-incompressible.[1–4] The ReB2 is expected to be able to scratch even diamond.[7,8] Transition metal borides often show refractory behavior and chemical inertness suitable for heavy duty coarse condition applications. Attractive electronic band structure-related features in some of the metallic borides (e.g., significant optical conductivity, reasonable electronic density of states at the Fermi level, non-selective and high value of reflectivity, etc.)[9,10] make them suitable for a variety of potential electronic and optoelectronic applications. Materials with high hardness values are used under extreme pressure and temperature conditions. Their applications as cutting tools and in hard coating are well documented.[11] Therefore, the studying and understanding of the thermo-mechanical properties of these transition metal borides are of substantial importance. In addition, various metallic borides (e.g., Mg, V, Cr, Mn, Co borides) have significant prospects for being used as hydrogen storage materials.[12] Electrically conducting (metallic) boride compounds not only give rise to the formation of one-, two-, or three-dimensional arrangements of covalently bonded boron atoms, but also, due to intricate structural features, offers a multitude of electronic interactions that can lead to superconductivity or various types of magnetic orders.[13–28] In recent years Nb–Ru–B systems have aroused the considerable interest of the materials science community.[29]

Till now, only four types of Nb–Ru–B ternary borides have been reported and investigated, namely, Nb7Ru6B8, Nb3Ru5B2, Nb2RuB2, and NbRuB.[5,29–32] The arrangement of the boron atoms in these compounds depends strongly on the metal element–boron (M/B) ratio. A number of different structural schemes are found with boron substructures ranging from isolated boron atoms to boron fragments or chains.[33] A special type of this phase has been the subject of several research groups — borides containing a sheet arrangement of atoms which leads to the separation of isolated boron atoms in one layer and boron fragments in the other, with metal atoms present in each layer. Recently, Mbarki et al.[29] succeeded in synthesizing NbRuB transition metal ternary boride by arc-melting the elements in water-cooled crucibles kept in argon atmosphere. This compound shows a layered structure with an orthorhombic space group Pmma. The NbRuB consists of two layers, one contains the Nb and an isolated B atom, and the other comprises the Ru atoms and boron fragments (dumbbell shaped B2 cluster).

A number of theoretical studies have been carried out in Nb–Ru–B systems.[5,29,32,34–36] Mbarki et al.[29] studied the electronic structure and the bonding properties of NbRuB by using the generalized gradient approximation/linear muffin tin–orbital (GGA-LMTO) formalism. This study predicted metallic behavior for NbRuB with the strongest bonding between the B atoms in the dumbbell situated in the same layer. Ab-initio investigations of the structural and elastic properties of predicted Nb2MB2 (M = Tc, Ru, Os) phases under hydrostatic pressure were conducted by Li et al.[36] Similar ambient pressure properties were studied by the same group.[36] Touzani et al.[34] theoretically examined the influences of bonding properties and electronic structures on the bulk and shear modulus of A2MB2 series (A = Nb, Ta, and M = Fe, Ru, Os).

Very few theoretical studies exist for the recently synthesized NbRuB compound. Besides, the studies by Mbarki et al.,[29] Tian and Chen[35] focused mainly on thermodynamic and superconducting state properties of this ternary transition metal boride system. To the best of our knowledge, no study of optical properties exists in the literature. A comprehensive study of thermodynamical properties is also lacking. In this study we are to fill these voids. Investigation of optical properties complements the electronic band structure calculations. Photon polarization dependent studies can reveal valuable information regarding any underlying electronic anisotropy. Moreover, these hard transition metal ternary borides may have potential optoelectronic utilities. To explore this possibility, optical study is essential. In this paper we study the structural, elastic, thermal, electronic and optical properties of NbRuB by using the density functional theory (DFT). Pressure and temperature dependence of the bulk modulus and the volume thermal expansion coefficient are also investigated. We also use the quasi-harmonic Debye approximation to explore the behaviors of Debye temperature and specific heat of NbRuB at various pressures and temperatures.

The rest of this paper is organized as follows. In Section 2 the computational methodology is described briefly. Various theoretical results are presented, analyzed and discussed in Section 3. Finally, the important conclusions from this study are stated and briefly elaborated in Section 4.

2. Computational method

The ab-initio calculations presented in this paper were carried out using the Cambridge Serial Total Energy Package (CASTEP) code.[37] The CASTEP employs the plane wave pseudopotential approach based on the density functional theory.[38,39] In the first-principles calculations the choice of exchange-correlation potential is important. In this study we used both LDA (with Ceperley–Alder (CA) and Perdew–Zunger (PZ) functional) and GGA exchange correlation functional. LDA is good enough for determining the structural, elastic and vibrational properties in many cases, though the LDA has a tendency of underestimating the lattice constants and overestimating various elastic constants and moduli in certain compounds. The GGA is more reliable and realistic since it permits a variation in the electron density. Here we used GGA functional as parameterized by the Perdew–Burke–Ernzerhof (PBE) scheme.[40] The GGA relaxes the lattice constants due to the repulsive core–valence electron exchange correlation. Vanderbilt-type ultrasoft pseudopotentials were used to model the electron–ion interactions. This relaxed the norm-conserving criteria but produced a smooth and computation friendly pseudopotential. A 4 × 13 × 7 k-point mesh of Monkhorst–Pack scheme[41] was employed to sample the first Brillouin zone. During the calculations, a plane-wave cutoff kinetic energy of 500 eV was used to limit the number of plane waves within the expansion. For geometrical optimization, the crystal structures were fully relaxed by the widely employed Broyden–Fletcher–Goldfrab–Shanno (BFGS) scheme.[42] The convergence tolerances used for various parameters are as follows: energy = 1.0 × 10−5 eV/atom; maximum force = 0.03 eV/Å maximum stress = 0.05 GPa; maximum displacement = 0.001 Å self consistent field = 1.0 × 10−6 eV/atom.

The elastic constants and moduli were obtained by applying a set of finite homogeneous crystal deformations and calculating the resulting stresses, as implemented within the CASTEP code. The frequency-dependent optical properties of a compound were extracted from the estimated dielectric function, ε(ω) = ε1(ω) + iε2(ω), which describes the interactions of photons with electrons. The imaginary part, ε2(ω), of the dielectric function was calculated in the momentum representation of matrix elements between occupied and unoccupied electronic quantum states by employing the CASTEP supported formula given by

Here, Ω is the unit cell volume, ω the frequency of the incident photon, e the charge of an electron, the unit vector defining the incident electric field polarization, and and are the conduction and valence band wave functions at a given wave-vector k, respectively. The Kramers–Kronig transformation yields the real part ε1(ω) of the dielectric function from the corresponding imaginary part ε2(ω). The refractive index, the absorption spectrum, the energy loss-function, the reflectivity, and the optical conductivity (the real part) can be derived once ε1(ω) and ε2(ω) are known.[43] The intraband electronic contribution to the optical properties of metallic systems affects mainly the low-energy part of the spectrum. This can be corrected for the dielectric function by including an empirical Drude term with unscreened plasma frequency of 6 eV and a damping term of 0.05 eV.

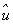
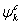
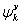
It should be mentioned that for the investigation of thermodynamic properties, we have used the energy–volume data calculated from the third-order Birch–Murnaghan equation of state[44] by using the zero temperature and zero pressure equilibrium values of energy, volume, and bulk modulus obtained through DFT calculations.

3. Results, analysis, and discussion
3.1. Structure of NbRuB

The optimized crystal structure (space group Pmma) of NbRuB is shown in Fig. 1. The structural parameters are listed and compared with available experimental and theoretical results in Table 1.

Fig. 1. (color online) Crystal structure of NbRuB, showing the layers with isolated boron atoms and boron dumbbells.
Table 1.

Optimized lattice parameters (a, b, c) and unit cell volume (V) of NbRuB.

.

From Table 1 it is seen that the equilibrium lattice parameters obtained with GGA accord quite well with the experimental values. The GGA underestimates the lattice parameters slightly. But we should keep in mind that the experimental lattice constants are extracted at room temperature while the ab-initio estimates are performed at absolute zero degrees. On the other hand LDA grossly underestimates the lattice parameters. This is somewhat expected due to the localized nature of the LDA functional.

The structure of NbRuB consists of two different layers stacked alternately along the crystallographic c direction. The first layer (the bottom one in Fig. 1) has Nb and B atoms, while the second one is filled with Ru and B2 dumbbells in addition to Nb. In NbRuB we can identify two different types of B atoms, one is situated in the center of a triangular prism with six Ru atoms at vertices and the other as B2 dimer inside a double-triangular prism constructed with Nb atoms.

3.2. Elastic properties

Table 2 exhibits the various elastic constants of NbRuB under ambient condition.

Table 2.

Independent single crystal elastic constants, Cij, (all expressed in unit GPa) of NbRuB at P = 0.

.

Table 3 shows the estimated elastic moduli of NbRuB.

Table 3.

Values of bulk modulus B, shear modulus G, Young’s modulus Y, B/G ratio, Poisson’s ratio ν, elastic anisotropy factor A, and the pressure derivative of bulk modulus B′ of NbRuB.

.

The single crystal elastic constants and the elastic moduli shown in Tables 2 and 3 completely determine the mechanical response of NbRuB under an applied external stress. The anisotropy factor A is obtained from the relation A = 2C44/(C11 − C12). It is seen that NbRuB possesses significant elastic anisotropy. For an isotropic compound A = 1. There is another measure of elastic anisotropy, kc/ka = (C11 + C12 − 2C13)/(C33 − C13). The value of kc/ka for NbRuB is 1.20. The kc and ka denote the compressibilities along the c and a direction, respectively. This implies that the compressibility of NbRuB along the c direction is larger than that within the ab plane. The LDA estimates of elastic moduli are somewhat larger than those from GGA, which is expected.

Calculated elastic constants, Cij, fulfill the various inequality criteria for mechanical stability.[45] The bulk and shear moduli of NbRuB are greater than those for Nb2RuB2 (B = 272 GPa and G = 146 GPa).[30] The difference between single crystalline elastic constants, (C12 − C44), is well known as the Cauchy pressure.[46] A positive value of (C12 − C44) indicates the metallic bonding, whereas a negative value signifies covalent bonding. According to this scheme, we find that NbRuB has predominantly metallic bonding in its structure. A positive Cauchy pressure always indicates the ductile nature of a material, while a negative value corresponds to brittleness. Hence the ternary boride NbRuB should behave in a ductile manner. Bulk modulus of NbRuB is also larger than that of Nb2TcB2 (284 GPa). The Nb2OsB2, on the other hand, has a larger bulk modulus (estimated to be 354 GPa)[36] than NbRuB. Both bulk modulus and the shear modulus give rough estimate of the hardness of a compound. Tian and Chen have estimated the hardness of NbRuB[35] to be about 15 GPa. This corresponds quite well with the result obtained in this work.[11] The parameter, B/G, is known as the Pugh’s ratio[47] which distinguishes between ductile and brittle response of a compound under applied stress. The critical value of Pugh’s ratio is estimated to be 1.75. A larger value indicates the ductile behavior. Another criterion often used to differentiate between ductile and brittle behavior is the Poisson’s ratio, ν. A Poisson’s ratio greater than 0.26 implies the ductile behavior. Therefore, both Pugh’s ratio and Poisson’s ratio predict moderately ductile response to stress for NbRuB ternary boride. All these support the predictions from Cauchy pressure analysis.

3.3. Thermal- and pressure-dependent properties

Hard and superhard transition metal borides are often used under extreme conditions of pressure and temperature. Therefore, information regarding the response of the bulk modulus, coefficient of thermal expansion, etc. at various elevated pressures and temperatures is important.

As mentioned earlier, we have used quasi-harmonic Debye approximation as implemented within the GIBBS program[48] to calculate the temperature-dependent elastic moduli and other thermodynamic parameters. This computationally efficient scheme has been used extensively for a variety of compounds with satisfactory results. Details of the computational procedures used in this study can be found in Refs. [49] and [50]. Figure 2(a) shows the variation of the bulk modulus with pressure. The bulk modulus of NbRuB increases quite sharply with increasing hydrostatic pressure, which is consistent with the high calculated value of B′ (Table 3). The temperature-dependent bulk modulus is shown in Fig. 2(b). It is seen that at low temperature, the bulk modulus remains almost constant, a standard behavior relating to the third law of thermodynamics.[51] A quasi-linear decrease of the bulk modulus at higher temperature is observed.

Fig. 2. (color online) (a) pressure- and (b) temperature-dependent bulk modulus of NbRuB.

The temperature- and pressure-dependent volume thermal expansion coefficients, αV, are shown in Figs. 3(a) and 3(b), respectively. Like all the elastic constants, volume thermal expansion coefficient is also directly related to the bonding property of a solid. The melting point of a solid often shows an inverse relationship with αV. The αV of NbRuB increases sharply at low temperatures but flattens above 400 K. αV decreases with applied pressure increasing. The rate of this decrement is higher at low pressure.

Fig. 3. (color online) (a) Temperature-dependent and (b) pressure-dependent volume thermal expansion coefficient of NbRuB.

Debye temperature is a fundamental material parameter. From the magnitude of Debye temperature we can estimate a number of important physical properties of solids namely, melting temperature, phonon specific heat, lattice thermal conductivity, etc. It is also related to the bonding strength among the atoms present within the crystal. Debye temperature sets a characteristic energy scale for phonon-mediated superconductor. The temperature-dependent and the pressure-dependent Debye temperatures of NbRuB are shown in Figs. 4(a) and 4(b), respectively.

Fig. 4. (color online) (a) Temperature-dependent and (b) pressure-dependent Debye temperature of NbRuB.

The zero temperature and zero pressure Debye temperature, θD, is found to be 594 K. This reasonably high Debye temperature for NbRuB indicates that this compound should have quite high lattice thermal conductivity. Light mass and strong covalent bondings among the B atoms are possibly responsible for this large Debye temperature. Tian and Chen[35] calculated Debye temperature from the elastic constants and found it to be 578.6 K, close to the value obtained here. Xie and Luo,[32] on the other hand, obtained θD from the analysis of heat capacity and found it to be 468 K, which is substantially lower than the value found in this study. The behaviors of material under different thermodynamical constraints are related to its specific heat. It also determines how efficiently a solid stores heats under different conditions of constant pressure or constant volume. The phonon contribution dominates both the specific heats at constant volume (Cv) and constant pressure (Cp) at high temperatures. Figure 5 shows the variations of molar heat capacities of NbRuB with temperature. The low-T specific heat shows a T3 variation in accordance with the Debye model, whereas at high-T both Cv and Cp approach the corresponding classical Dulong–Petit values.

Fig. 5. (color online) Temperature-dependent specific heats of NbRuB. The red line shows the Dulong–Petit limit.
3.4. Electronic band structure and energy density of states of NbRuB

The variation of electronic energy state with electron wave vector leads to the electronic band structure. The study of electronic band structure is essential for comprehending all the electronic transport and optical properties of a material. It also provides us with important information regarding the natures of chemical bonding and structural features. The result of band structure calculation along the highly symmetric direction within the k-space is shown in Fig. 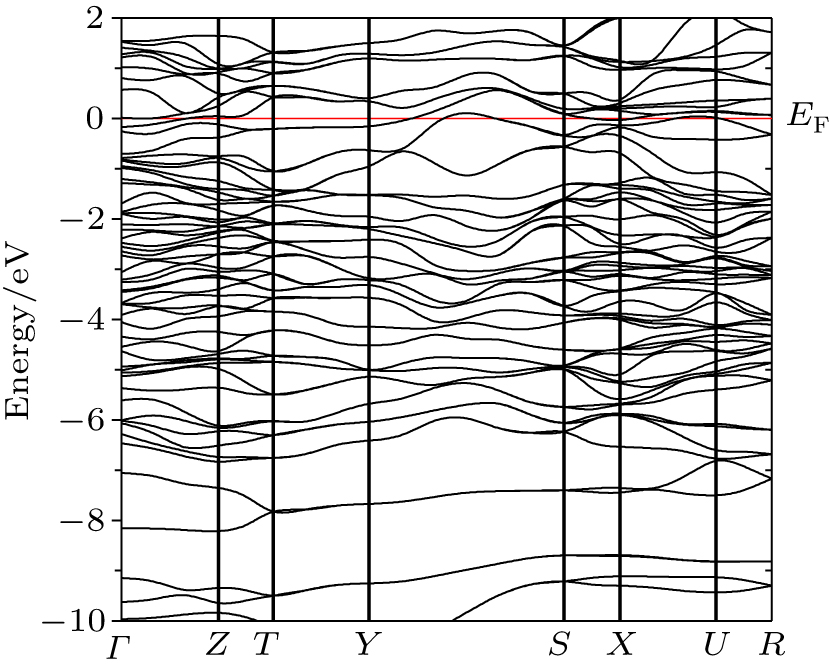6. The horizontal dashed line is drawn as the Fermi level. It is seen that there are several dispersive bands cross the Fermi level, especially along the Y–S direction. There is also appreciable band overlap between valence and conduction states. All these imply that NbRuB should exhibit metallic conductivity. The detailed features of band structure and their roles in various electronic phenomena can be explained with the calculated total and partial densities of states. These electronic energy densities of states, obtained using the GGA functional are shown in Fig. 7.

Fig. 6. (color online) Electronic band structure of NbRuB along the high symmetry directions in the Brillouin zone.
Fig. 7. (color online) Total and partial electron energy density of states.

The electron energy density of states (DOS) of a system determines the number of quantum states per unit interval of energy at each energy level that is available to be occupied by electrons, and is normalized to volume or unit cell. The density of states for a given band n, Nn(E), is defined in three dimensions as

where En(k) describes the dispersion of the given band and the integral is carried over the first Brillouin zone. The total energy density of states, N(E), is obtained by summing over all bands:
Figure 7(a) shows a large value of N(EF), 10.2 states/eV-cell reassuring the metallic character of NbRuB. The atomically resolved partial DOS (PDOS) provides us with more information regarding the incipient electronic structure. It is seen from Fig. 7 that the low-energy valence band states (below −10 eV to ~ −7 eV) are primarily derived from the B 1s states. The d-orbitals of Nb and Ru contribute moderately to low-energy total DOS (TDOS). B 2p, Ru 4d, and Nb 4d orbitals dominate in the intermediate energy range (from −7 eV to below the Fermi energy). Electronic states located at the levels of and above EF are delocalized and take part in various transport phenomena. It is seen from Fig. 7 that the TDOS around the Fermi energy arises from almost equal contributions due to 4d electronic orbitals of Nb and Ru atoms. Significant N(EF) implies that electronic contribution to the heat capacity and thermal conductivity should be appreciable in this transition metal ternary boride. Figure 7 indicates that there is significant hybridization among the B 2p, Nb 4d, and Ru 4d orbitals in the vicinity and below the Fermi level. These orbitals participate in the inter-atomic bonding of the crystal. There is a noticeable pseudogap just below the Fermi energy at ~ −0.75 eV. The 2p electronic states of B give rise to strong covalency among B atoms and significantly contribute to the hardness of the material. The 4d electronic orbitals of Nb and Ru and the 2p states of the B atom have strong directional characteristics. Therefore, these orbitals should contribute to covalent bondings in NbRuB.

3.5. Optical properties of NbRuB

Optical properties of a material are closely related to the material response to incident electromagnetic radiation. The response to visible light is particularly important from the view of optoelectronic applications. The response to the incident radiation is completely determined by the various energy-dependent (frequency) optical parameters, namely real and imaginary part of dielectric constants, ε1(ω) and ε2(ω), respectively, real part of refractive index (n(ω)), extinction coefficient (k(ω)), loss function (L(ω)), real and imaginary parts of optical conductivity (σ1(ω) and σ2(ω), respectively), reflectivity (R(ω)), and the absorption coefficient (α(ω)). The calculated optical constants of NbRuB for photon energies up to 16 eV with electric field polarization vectors along [100] and [001] directions are shown in Fig. 8. As mentioned earlier, polarization-dependent optical parameters yield the information regarding optical and electronic anisotropy.

Fig. 8. (color online) Variations of (a) dielectric constant, (b) refractive index, (c) loss function, (d) optical conductivity, (e) reflectivity, and (f) absorption coefficient of NbRuB with energy for different electric field polarizations.

Figure 8(a) shows the real and imaginary parts of the dielectric constants. Both ε1(ω) and ε2(ω) show metallic characteristics.[52] For metallic systems, in the low-frequency region where ωτ ≪ 1, the imaginary part of the dielectric constant dominates the optical behavior. On the other hand, when ωτ ≫ 1 (high frequency region), the real part approaches unity (which cannot be seen clearly in Fig. 8(a) because of the large vertical scale) and the imaginary part becomes very small. Here, τ is the electron relaxation time. On an expanded vertical scale, it can be seen that the real part of the dielectric constant crosses zero at ~ 13 eV and approaches unity and the imaginary part tends to zero at ~ 12 eV. Therefore the material becomes transparent to incident electromagnetic radiation.

The energy dependence of real and imaginary parts of the refractive indices are given in Fig. 8(b). The real part of the refractive index determines the phase velocity of the electromagnetic wave inside the sample, while the imaginary part, often termed extinction coefficient, gives the measure of the attenuation when the electromagnetic wave travels through the material. Both the real and imaginary part of the refractive index are related to the dielectric constant via the relations ε1(ω) = n2(ω) – k2(ω) and ε2(ω) = 2n(ω)k(ω).[53] Therefore, at high energies both real and imaginary parts of the refractive index become small since the imaginary part of the dielectric constant approaches zero as exhibited in Fig. 8(b). Slight polarization-dependent anisotropy in the dielectric function is converted into slight anisotropy in the frequency-dependent refractive index. This anisotropy, though still low, is relatively pronounced near ~ 6 eV.

The energy-dependent loss function is shown in Fig. 8(c). The energy loss function, L(ω), of a material is an important parameter in the optical property study which is useful for understanding the screened excitation spectra, especially the collective excitations produced by the swift charges traversing a solid. The highest peak of the energy loss spectrum appears at a particular incident light frequency (energy) known as the bulk screened plasma frequency. A sharp electromagnetic loss peak is seen in Fig. 8(c). This implies that the underlying excitation spectrum is quite monochromatic. The screened plasma frequency for recently discovered NbRuB is found to be ~ 15 eV. The loss spectrum is quite isotropic with respect to the polarization of the incident radiation.

Optical conductivity spectra are shown in Fig. 8(d). The real part of the energy-dependent optical conductivity represents the in-phase current which produces the resistive joule heating, while the imaginary part determines the π/2 out-of-phase inductive current. At low frequencies both σ1(ω) and σ2(ω) are proportional to the Drude conductivity. It is seen from Fig. 8(d) that the low-frequency conductivities are high. This shows that NbRuB has good metallic characteristics. The real and imaginary parts of the optical conductivity show broad peaks at ~ 3 eV and ~ 4.5 eV, respectively. Therefore, NbRuB should exhibit significant optical conductivity in the visible range of electromagnetic spectrum. In the high-frequency region, above 7 eV, σ1(ω)≪ σ2(ω), and the electrons display an essentially inductive character. No energy is absorbed from the electromagnetic field and no joule heat appears. Optical conductivity is found to be fairly isotropic.

The reflectivity is the ratio of the energy of a wave reflected from a surface to the energy of the wave incident on it. The reflectivity spectrum is exhibited in Fig. 8(e). The R(ω) rises sharply at around 15 eV, close to the plasma edge. Strong metallic reflection dominates at energies below 15 eV. There are two shallow dips in the reflectivity spectrum centered at ~ 2 eV and ~ 10 eV respectively. The reflectivity spectrum shows almost no polarization dependence. Barring those shallow dips, R(ω) remains high from infra-red to near ultraviolet energies, without any strong selective characteristic.

Figure 8(f) illustrates the absorption spectra. The absorption coefficient gives a measure of the distance that a light of a particular wavelength (energy) can penetrate into a material before it is absorbed. It also provides us with the information about the optimum solar energy conversion efficiency. The absorption spectrum rises sharply above 2 eV, reaches a maximum value of around 5 eV and decreases to almost zero at and above 15 eV. The broad peak in α(ω) involves optical transitions of electrons among B 2p, Ru 4d, and Nb 4d electronic orbitals.

3.6. Superconducting state properties of NbRuB

NbRuB exhibits conventional BCS superconductivity at 3.1 K.[35] We calculate the electron–phonon coupling constant, λe-ph, from the Tc equation due to McMillan[54] with the estimated Debye temperature of 594 K and an assumed repulsive Coulomb pseudopotential, μ, of 0.10 (a typical value). This analysis yields λe-ph = 0.431. Therefore, NbRuB can be considered as a weakly coupled phonon-mediated Bardeen–Cooper–Schrieffer (BCS) superconductor. These results accord quite well with those found by Tian and Chen.[35]

4. Conclusions

First-principles DFT-based calculations are performed to investigate the elastic, thermal, electronic, and optical properties of recently discovered transition metal ternary boride NbRuB. The optical properties are investigated for the first time. Some of the thermodynamic properties are also explored theoretically using the quasi-harmonic Debye approximation for the first time. The structural parameters obtained from the optimized geometry within the GGA show excellent agreement with those found by previous experimental and theoretical studies.[29,32,35] The estimated elastic constants and moduli show fair correspondence with previous estimates.[35] These elastic constants fulfill Born criteria of mechanical stability. The NbRuB shows significant elastic anisotropy. The material is markedly more compressible along the c axis than along other crystallographic directions. Relatively high values of bulk and shear moduli (298.3 GPa and 155.4 GPa, respectively) of NbRuB show that it has a potential to be used as a moderately hard material. A positive Cauchy pressure implies that metallic bonding dominates in the NbRuB. Electronic band structure calculations, on the other hand, show some relevance to covalent bonding, especially for B–B bonding. The Poisson’s ratio predicts the characteristic of interatomic forces in solid. A material is said to be a central force solid when Poisson’s ratio lies in a range from 0.25 to 0.50, otherwise it is a non-central force solid. Analysis of the Poisson’s ratio suggests that the structural stability is derived from central force in the NbRuB.

A hard material is able to resist the plastic deformation. It primarily involves preventing the dislocations from nucleating and moving, which leads to irreversible change within the structure. In general, a material with short covalent bonding has a tendency of restricting such a motion of dislocations and a material containing more delocalized bonds tolerates them. Accordingly, diamond, the hardest material known to date, has short covalent carbon–carbon bonding that shows high directionality with high strength. On the other hand, metallic compounds consisting of non-directional bonding and are usually soft and ductile due to having a characteristic sea of mobile electrons. As an exception to the norm, the NbRuB has both ductility and a fair degree of hardness, which can be quite useful for applications.

Pressure- and temperature-dependent behaviors of the bulk modulus, coefficient volume thermal expansion, and Debye temperature of NbRuB are studied. A high Debye temperature implies high interatomic force and a significant phonon thermal conductivity. The NbRuB is a weakly coupled phonon mediated BCS superconductor. It is interesting to note that Os containing ternary borides have stronger chemical bonding.[11] These compounds may have higher Debye temperatures and large electronic densities of states at the Fermi level. Such materials may exhibit superconductivities at higher temperature. The specific heat of NbRuB is calculated as a function of temperature. From the calculated value of N(EF), we obtain the coefficient of electronic specific heat, γe, given by . It shows that the specific heat is primarily dominated by the phonon contribution. At room temperature the electronic contribution is only around 2% of the total specific heat capacity.

The electronic band structure calculations are performed using both LDA and GGA. No significant difference can be seen. The gross features of calculated electronic band structure accord well with those found in other investigations.[32,35] The bands crossing the Fermi-level along different symmetry directions within the Brillouin zone are quite dispersive and no significant electronic anisotropy can be detected. The electronic density-of states spectrum shows that the Fermi level of NbRuB resides at the rising part of a deep pseudogap (Fig. 7), which indicates that there is scope to tune N(EF) to higher or lower values by appropriate chemical substitutions.

The optical constants are studied theoretically for the first time by using LDA and GGA functionals. Once again, no significant difference can be detected. All the optical constants are found to be quite isotropic with respect to the polarization of the incident electric field. The energy-dependent optical constants reveal strong metallic characteristics consistent with the electronic band structure calculations. The reflectivity spectra show some interesting characteristics. Barring two shallow dips, R(ω) remains high from infra-red to near ultraviolet energies (Fig. 8(e)). This non-selective nature of R(ω) can be useful for applications. The NbRuB has the potential to be used as an effectively reflecting material to reduce solar heating. The R(ω) characteristics of NbRuB are comparable to those of many MAX compounds in this regard.[50,52,54–59]

A primary challenge to modern material science is the innovative designs and syntheses of new compounds with attractive properties for novel applications. Amongst them, the search for hard materials is one of the very important subjects. Recently synthesized NbRuB possesses reasonable hardness, ductility, metallic electronic characteristics, non-selective highly reflective optical behavior, and conventional weak-coupling BCS superconductivity. The elastic anisotropy in NbRuB originates from anisotropy in the chemical bonding. We hope that this theoretical investigation of elastic, thermal, electronic, and optical properties of technologically promising, recently discovered NbRuB will stimulate further experimental and theoretical studies in the near future.

Reference
[1] Kanyanta V 2016 Microstructure — Property Correlations for Hard, Suparhard, and Ultrahard Materials Kanyanta V Springer Switzerland Ch. 1 1 23 10.1021/ja043806y
[2] Cumberland R W Weingberger M B Gilman J J Clark S M Tolbert S H Kaner R B 2005 J. Am. Chem. Soc. 127 7264
[3] Hebbache M Stuparevic L Zivkovic D 2006 Solid State Commun. 139 227
[4] Chung H Weinberger M B Yang J Tolbert S H Kaner R B 2008 Appl. Phys. Lett. 92 261904
[5] Touzani R St Fokwa B P T 2014 J. Solid State Chem. 211 227 and references therein
[6] Herbst J F Croat J J Pinkerton F E Yelon W B 1984 Phys. Rev. B 29 4176
[7] Levine J B Betts J B Garrett J D Guo S Q Eng J T Migliori A Kaner R B 2010 Acta Mater. 58 1530
[8] Chung H Weinberger M B Levine J B Kavner A Yang J Tolbert S H Kaner R B 2007 Science 316 436
[9] Werhcit H Kuhlmann U Krach G 1993 J. Alloys Compd. 202 269
[10] Hadi M A Nasir M T Roknuzzaman M Rayhan M A Naqib S H Islam A K M A 2016 Physica Status Solidi 253 2020
[11] Levine J B Tolbert S H Kaner R B 2009 Adv. Funct. Mater. 19 3519 and references therein.
[12] Li W Vajo J J Cumberland R W Liu P Hwang S-J Kim C Bowman R C Jr 2010 J. Phys. Chem. Lett. 1 69
[13] Rogl P Nowotny H 1978 J. Less Common Met. 61 39
[14] Nowotny H Rogl P 1977 Boron and Refractory Borides Matkovich V New York Springer Ch. 23 413 438 10.1002/chem.v21.46
[15] Kuz’ma Yu B 1983 Crystallochemistry of Borides Lviv Lviv University Publishers
[16] Rogl P 1991 Inorganic Reactions and Methods Hagen A P Wiley Ch. 20
[17] Zheng Q Wagner F R Ormeci A Prots Yu Burkhardt U Schmidt M Schnelle W Grin Yu Leithe-Jasper A 2015 Chem. Eur. J. 21 16532
[18] Ade M Hillebrecht H 2015 Inorg. Chem. 54 6122
[19] Vandenberg J M Matthias B T Corenzwit E Barz H 1975 Mat. Res. Bull. 10 889
[20] Ku H C Meisner G P Acker F Johnston D C 1980 Solid State Commun. 35 91
[21] Matthias B T Corenzwit E Vandenberg J M Barz H E 1977 Proc. Natl. Acad. Sci. USA 74 1334
[22] Zheng Q Gumeniuk R Rosner H Schnelle W Prots Y Burkhardt U Grin Y 2015 J. Phys.: Condens. Matter 27 415701
[23] Zheng Q Schnelle W Prots Y Bobnar M Burkhardt U Leithe-Jasper A Gumeniuk R 2016 Dalton Trans. 45 3943
[24] Gignoux D Schmitt D 1997 Handbook of Magnetic Materials 10 Buschow K H J Amsterdam North-Holland 239 10.1002/(ISSN)1521-3773
[25] Dronskowski R Korczak K Lueken H Jung W 2002 Angew. Chem. Int. Ed. 41 2528
[26] Isnard O Fruchart D 1994 J. Alloys Compd. 205 1
[27] Fokwa B P T 2010 Eur. J. Inorg. Chem. 2010 3075
[28] Mbarki M Touzani R St Fokwa B P T 2014 Angew. Chem. Int. Ed. 53 13174
[29] Mbarki M Touzani R St Fokwa B P T 2014 Eur. J. Inorg. Chem. 2014 1381
[30] Hermus M Geier D Fokwa B P T 2012 Z. Anorg. Allg. Chem. 638 49
[31] Zheng Q Kohout M Gumeniuk R Abramchuk N Borrmann H Prots Y Burkhardt U Schnelle W Akselrud L Gu H Leithe-Jasper A Grin Y 2012 Inorg. Chem. 51 7472
[32] Xie W W Luo H 2015 Chem. Mater. 27 1149
[33] Wiberg E Wiberg N Holleman A F 2001 Inorganic Chemistry San Diego Academic Press
[34] Touzani R St Rehorn C W G Fokwa B P T 2015 Comput. Mater. Sci. 104 52
[35] Tian W Chen H 2016 Scientific Reports 10.1038/srep19055
[36] Li X Yan H Wei Q 2016 Comput. Cond. Matter 10.1016/j.cocom.2016.02.001
[37] Clark S J Segall M D Pickard C J Hasnip P J Probert M I J Refson K Payne M C 2005 Z. Kristallographie 220 567
[38] Hohenberg P Kohn W 1964 Phys. Rev. 136 B864
[39] Kohn W Sham L J 1965 Phys. Rev. 140 A1133
[40] Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
[41] Monkhorst H J Pack J D 1976 Phys. Rev. 13 5188
[42] Fischer T H Almlof J 1992 J. Phys. Chem. 96 9768
[43] Saha S Sinha T P Mookerjee A 2000 Phys. Rev. 62 8828
[44] Birch F 1978 J. Geophys. Res.: Solid Earth 83 1257
[45] Beckstein O Kelpies J E Hart G L Pankratov O 2001 Phys. Rev. 63 134112
[46] Pettifor D 1992 Mater. Sci. Technol. 8 345
[47] Pugh S F 1954 Philos. Mag. 45 823
[48] Blanco M A Francisco E Luana V 2004 Comput. Phys. Commun. 158 57
[49] Hadi M A Roknuzzaman M Chroneos A Naqib S H Islam A K M A Vovk R V Ostrikov K 2017 Comput. Mater. Sci. 137 318
[50] Ali M A Nasir M T Khatun M R Islam A K M A Naqib S H 2016 Chin. Phys. 25 103102
[51] Wachtman J B Jr Tefft W E Jr Lam D J Jr Apstein C S 1961 Phys. Rev. 122 1754
[52] Roknuzzaman M Hadi M A Abden M J Nasir M T Islam A K M A Ali M S Ostrikov K Naqib S H 2016 Comput. Mater. Sci. 113 148
[53] Kittel C 1996 Introduction to Solid State Physics 7 Wiley 10.1103/PhysRev.167.331
[54] McMillan W L 1968 Phys. Rev. 167 331
[55] Nasir M T Hadi M A Naqib S H Parvin F Islam A K M A Ali M S Roknuzzaman M 2014 Int. J. Mod. Phys. 28 1550022
[56] Ali M S Rayhan M A Ali M A Parvin R Islam A K M A 2016 J. Sci. Res. 8 109
[57] Hadi M A Roknuzzaman M Parvin F Naqib S H Islam A K M A Aftabuzzaman M 2014 J. Sci. Res. 6 11
[58] Ali M S Parvin F Islam A K M A Hossain M A 2013 Comput. Mater. Sci. 74 119
[59] Ali M S Islam A K M A Hossain M M Parvin F 2012 Physica 407 4221