Xing Jiao-jiao, Wu Zi-hua, Xie Hua-qing, Wang Yuan-yuan, Li Yi-huai, Mao Jian-hui. Performance of thermoelectric generator with graphene nanofluid cooling. Chinese Physics B, 2017, 26(10): 104401
Permissions
Performance of thermoelectric generator with graphene nanofluid cooling
Xing Jiao-jiao, Wu Zi-hua †, Xie Hua-qing, Wang Yuan-yuan, Li Yi-huai, Mao Jian-hui
School of Environmental and Materials Engineering, Shanghai Polytechnic University, Shanghai 201209, China
Project supported by the Major Program of the National Natural Science Foundation of China (Grant No. 51590902), the National Natural Science Foundation of China (Grant N. 51476095), and the Program for Professor of Special Appointment (Young Eastern Scholar, QD2015052) at Shanghai Institutions of Higher Learning, and the Natural Science Foundation of Shanghai (Grant No. 14ZR1417000).
Abstract
Improvement of the heat transfer of the cold side is one of the approaches to enhance the performance of TEG systems. As a new type of heat transfer media, nanofluids can enhance the heat transfer performance of working liquid significantly. Based on a three-dimensional and steady-state numerical model,the heat transfer and thermoelectric conversion properties of TEG systems were studied. Graphene anoplatelet aqueous nanofluids were used as the coolants for the cold side of the TEG system to improve the heat transfer capacity of the cold side. The results showed that the heat absorbed by the hot side, voltage, output power, and conversion efficiency of the TEG system were increased greatly by the nanofluid coolants. The output power and the conversion efficiency using 0.1-wt% graphene nanoplatelet aqueous nanofluid as the coolant are enhanced by 26.39% and 14.74%, respectively.
With the diminishing reserve of primary energy and the rising concern on waste heat recycle applications, much more attention has been drawn by thermoelectric generation (TEG) recently.[1,2] Compared to the traditional energy conversion devices, TEG systems have the noteworthy advantages of simple structures, without moving parts, environmental friendliness, silence, reliability, and excellent scalability. However, TEG technology has had little further development and application because of the low conversion efficiency. In the past few decades, with the development of material science, the conversion efficiency of TEG has been improved greatly.[3] Nowadays, this technology has commonly been used in waste heat recycle systems for aerospace, remote power, military, and photovoltaic thermal (PV/T) collectors.[4–6] Many researchers analyzed the waste heat recovery and the optimization of the TEG system. Moreover, the thermal resistance and thermal loss have also been considered. Gou et al. reported a dynamic model for the TEG system applied in waste heat recovery.[7] Jia et al. proposed an optimal design of a novel TEG system with linear-shaped structure under different operating temperatures.[8] Bimrew et al. studied the effects of the thermal contact resistance and Thomson heating on the outputs of solar thermoelectric power generation system.[9] Meng et al. established a numerical model and comparatively investigated the TEG system with multi-irreversibilities.[10] Feng et al. successfully developed a thermoelectric power generation device with bismuth telluride/cobalt structure; the measured conversion efficiency of the TEG device was 12% under the temperature difference of 541 °C.[11] International transport property-measurement round-robins have been conducted by the thermoelectric annex under the International Energy Agency (IEA) Implementing Agreement on Advanced Materials for Transportation (AMT). The study intentionally included multiple testing methods and instrument types. Over the full temperature range, the measurement discrepancies for the figure of merit, ZT, in this round-robin were ± 11.5% to ± 16.4% from the averages.[12]
In the TEG process, the heat converts into electrical energy partly by the TEG system, and the rest is mainly transferred to the heat sink. The efficiency of the TEG system depends on the temperature difference between the hot and cold sides of the TEG legs, which is determined by the heat source and the cooling method. The thermal capabilities of the heat source and heat sink have a strong impact on the efficiency of the system. When the temperature of the heat source was fixed, the thermal transport capability of the working fluid of the heat sink directly affected the output performance of the TEG system. Meir et al.[13] investigated the highly-efficient thermal-electrical conversion of solar energy by a TEG system. Enescu et al.[14] made a review of the literature focusing on the thermoelectric cooling parameters and performance. Chen et al.[15] investigated the geometric effect on the cooling power and performance of an integrated thermoelectric generation-cooling system. Huang et al.[16] studied the geometry optimization of thermoelectric coolers using a simplified conjugate-gradient method. Favarel et al.[17] numerically studied the optimization of the occupancy rate on the cold side of a TEG system to produce the highest electrical power. Zhou et al.[18] made an analysis of the output performance of the TEG system in different inlet temperatures and mass flow rates of the coolant. In addition to improving device geometry and operation conditions, selecting working fluids is another way to optimize the TEG system.
As studied by many in the literature,[19–25] conventional thermal energy utilization systems’ nanofluids were found to exhibit better thermo-physical properties such as higher thermal conductivity, higher thermal diffusivity, and higher viscosity than those of base fluids. Zhou et al.[26] increased the thermal transport capability of water for the TEG cooling system with CuO nanoparticles added. It was found that the conversion efficiency of the nanofluid-cooled TEG system was 14% higher than that of the pure water-cooled one. The heat transfer coefficient of a certain type of nanofluid depends on several other factors, such as thermal conductivity and specific heat capacity of the base fluid and nanoparticles, the flow pattern, the viscosity of the nanofluid, the concentration of the suspended nano-particles, the dimensions and the shape of the particles as well as the flow structure. The thermal conductivity of nanoparticles is vital among those factors. Graphene has a unique two-dimensional (2D) structure and it has attracted a great deal of interest due to its excellent mechanical, electrical and thermal properties. The thermal conductivity of Graphene is reported to be as high as 3000 W/mK–5000 W/mK. The literature[27] improved the understanding of the relation of heat transfer and thermophysical properties for nanofluids by investigating the effect of specific surface area (300, 500, 750 m2/g) of a graphene nanoplatelet (GNP) nanofluid on the heat transfer coefficient and friction factor. This paper further studied the effect of graphene nanoplatelet nanofluid coolants on the TEG system with temperature-dependent thermoelectric material properties. The use of graphene nanoplatelets can reduce the deposition and promote the uniformity of nanofluilds. Thermoelectric and Fluent modules in Ansys workbench surroundings are used for the numerical simulation. The rest of this paper is organized as follows. In Section 2, the numerical models and the physical models applied are described. The detailed results and discussions are presented in Section 3. Finally, we conclude in Section 4.
2. Numerical implementation
2.1. Numerical model
Based on the numerical heat transfer (NHT) theory the numerical discretization process is as follows: the continuous physical field in space and time coordinates are replaced by a set of values on a finite set of discrete points. Then the discretization equations of the relationship between these discrete point variables are established by a continuity equation, momentum equation, and energy equation. Finally we apply a numerical calculation to solve these equations.
2.1.1. Heat exchanger model
Graphene nanoplatelet aqueous nanofluids are used as the coolant with the specific surface area of the GNPS of 750 m2/g and the concentrations of 0.025 wt%, 0.05 wt%, 0.075 wt%, and 0.1 wt%.
Nanofluid density ρ can be calculated as
where ϕ is the concentration of graphene nanoplatelet. The expression of specific heat capacity Cp of the nanofluid is
The parameters of distilled water and graphene nano-platelets, including the density of distilled water ρw, specific heat capacity of distilled water Cpw, density of graphene nanoplatelets ρg, specific heat capacity of graphene nano-platelets Cpg, can be found in Table 1, while the parameters of nanofluids, including thermal conductivity of nanofluid λ and kinematic viscosity of nanofluid ν are listed in Table 2.
Table 1.
Table 1.
Table 1.
Physical parameters of distilled water and graphene nano-platelets.[27,28]
.
ρw/kg·m−3
ρg/kg·m−3
Cpw/J·kg−1·K−1
Cpg/J·kg−1·K−1
997
2250
4181.7
1400
Table 1.
Physical parameters of distilled water and graphene nano-platelets.[27,28]
.
Table 2.
Table 2.
Table 2.
Physical parameters of nanofluids.
.
λ/W·m−1·K−1
ν/10−7 m2·s−1
ρ/kg·m−3
Cp/J·kg−1·K−1
Distilled water
0.6
7.47797
997
4181.7
0.025-wt% graphene-dispersed nanofluids
0.68
8.94441
1028.575
3952.767
0.05-wt% graphene-dispersed nanofluids
0.705
9.24397
1060.15
3737.470
0.075-wt% graphene-dispersed nanofluids
0.73
9.52621
1091.725
3534.628
0.1-wt% graphene-dispersed nanofluids
0.752
9.97062
1123.3
3343.188
Table 2.
Physical parameters of nanofluids.
.
When the coolant is in the full development stage of laminar flow and the effect of the variation of the physical properties is ignored, the Zader–Tate equation can be applied to describe the average Nusselt number for the distance l of 0.052 m as follows:
where Re = ude/ν is the Reynolds number, Pr = ρνcp/λ is the Prandtl number, and de = 4Af/B is the equivalent diameter. In the above equations, u is the flow rate, ν is the kinematic viscosity, λ is the thermal conductivity, Af is the viscosity, B is the wetted perimeter, and h = λNu/l is the heat transfer coefficient.
2.1.2. Thermoelectrical analogy model
For the thermoelectric mode, the conductions of heat at Th of the p-type leg, and Tc of the n-type leg are as follows:[29]
where S(Th) is the Seebeck coefficient at Th, and Rp and Rn are T-dependent electrical resistances at a given thermal boundary, defined as . The terms on the right-hand side of Eqs. (4) and (5) represent Peltier, conduction, Joule, and Thomson heats, respectively. Total input heat Qh at Th is Qh,p + Qh,n.
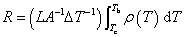
The closed circuit voltage U equals to the open circuit voltage Uint when the load electrical resistance (R0) equals the internal one (Rint = Rp + Rn), whose expression is
The output power is
where m is the ratio of load electrical resistance (R0) to the internal electrical resistance (Rint = Rp + Rn),
The conversion efficiency of the module is expressed as
2.2. Physical model
A TEG system consists of TEG module, cooling system, and heating plate.
In the TEG system, the heat converts into electrical energy partly in a closed loop with external resistance by a heating plate, and the rest is mainly transferred to the heat sink. Waste heat energy can provide continuous heat. Here, the heating plate is applied to realize the effect of a normal waste heat source. The heating plate is fixed to 400 °C.
In the TEG module, eight p-type and n-type semiconductors, copper conducting strips constitute a TEG module as illustrated in Fig. 1. The semiconductors are connected thermally in parallel, and electrically in series. Commercially available p-type semiconductor material Bi0.25Sb0.75Te3 and n-type semiconductor PbTe are used as the materials for TEG. The TEG leg in the simulations is 0.01 m × 0.01 m × 0.01 m, capped by thin copper electrodes with the height of 1 mm. When the TEG model connects external resistance, the output voltage will display in the voltmeter. The external resistance is set to 0.036 Ω, in order to obtain the maximum electrical power when R0 = Rint.
Fig. 1. (color online) Schematic diagram of the TEG model and cooling structure.
By the power of the pump, the cooling fluid flows through the heat exchanger, liquid cabin pump, and condenser in turn. The fluid is heated through the heat sink, liquid cabin, pump, cooled by the condenser and returns to the heat sink finally.
In this study, graphene nanoplatelet aqueous nanofluids were used as coolants for the cold side to enhance the conversion capability of the TEG system. Due to the relatively high specific heat capacity of the coolant, the temperature variation of the coolant is negligible. The inlet temperature of the coolant is set to 303 K.
The following assumptions are made, which are reasonable and will not affect the universality of the simulated results. The thermal resistances through the exhaust tube wall, cooling tube wall, and ceramic plates are ignored. The heat loss between n-type and p-type semiconductors is also ignored. The radiation heat loss is not considered. The surroundings are in good insulation.
3. Results and discussions
A steady state model of the TEG system was then established and analyzed in the ANSYS workbench environment based on the finite element method. Following the method described in Ref. [28], distilled water was loaded with graphene nanoplatelets with the weight fractions of 0.025 wt%, 0.05 wt%, 0.075 wt%, and 0.1 wt%, respectively. Then, the as prepared graphene-dispersed nanofluids were used as coolants for the cold side of the TEG system.
The convection heat transfer coefficients using different coolants are presented in Fig. 2. It is shown that the convection heat transfer coefficient, h, has an incremental tendency with the increase of the flow rate. The enhancement becomes slow when the Reynolds number is larger than about 250. When the nanofluids are applied as the coolant, h becomes larger than the case with only basic fluid used as the coolant. The convection heat transfer coefficient h increases with the increase of the weight fraction of the graphene nanoplatelets. It can be seen from Fig. 3 that the enhancement ratio of h is 11.39%, 16.37%, 20.18%, and 24.87% for 0.025 wt%, 0.05 wt%, 0.075 wt%, and 0.1 wt% graphene-dispersed nanofluid adopted as coolant, respectively. It is interesting that the Reynolds number does not have much influence on the enhancement ratio of h.
Fig. 3. (color online) Enhancement ratio of the heat transfer coefficient as a function of Reynolds number with nanofluids as coolants.
The 3D electric potential contours for the TEG system at the Reynolds number of 1675 are described in Fig. 4. It is shown that the larger heat transfer capability of the coolant leads to a larger electrical potential difference of the TEG system. The output electric potential captured is about 0.52229 V for the TEG system with distilled water as coolant (see Fig. 4(a)). The output electric potentials are 0.5282 V, 0.53045 V, 0.53205 V, and 0.53388 V for the TEG systems with 0.025-wt% (Fig. 4(b)), 0.05-wt% (Fig. 4(c)), 0.075-wt% (Fig. 4(d)), and 0.1-wt% (Fig. 4(e)) graphene-dispersed nanofluids as coolants, respectively.
Fig. 4. (color online) Electric potential contours for the TEG system with (a) base fluid, (b) 0.025-wt% graphene-dispersed nanofluids, (c) 0.05-wt% graphene-dispersed nanofluid, (d) 0.075-wt% graphene-dispersed nanofluid, and (e) 0.1-wt% graphene-dispersed nanofluid used as the coolants.
Figures 5 and 6 show the dependences of the heat absorbed by the hot side, Q, and its enhancement ratio on the flow rate of the coolant on the Reynolds number. It can be seen from Fig. 5 that Q increases with the increase of the Reynolds number. Q increases quickly with increasing the Reynolds number when the Reynolds number is smaller than 300, while Q increases much more slowly when the Reynolds number is larger than 300. In Fig. 6, it is found that the enhancement rate of Q decreases sharply with the Reynolds number at a low Reynolds number, and it decreases much more slowly when the Reynolds number is higher than 300. The enhancement rates of Q are 3.46%, 4.84%, 5.85%, 7.03% at the Reynolds number of about 15 for 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluid as coolant, respectively. These results show that the heat absorbed by the hot side is substantially enhanced with the nanofluids as coolants for the cold side of the TEG system. It indicates that the waste heat recovery capacity would be improved when the nanofluids are used as the coolants for the cold side while the TEG system is employed in waste heat recovery applications.
Fig. 6. (color online) Enhancement ratio of the heat absorbed by the hot side of the TEG system as a function of Reynolds number with different coolants.
The voltage of a TEG system highly depends on the heat absorbed by the hot side. Figure 7 shows the flow rate of the coolant dependent voltage of the TEG systems, U, with different cold side conditions. The variation tendency of U is similar to that of Q shown in Fig. 5. Since the heat transfer capacity of the coolant is enhanced by increasing the flow rate, Q becomes larger, and hence the voltage of the TEG is increased. In order to demonstrate the effect of the nanofluid coolants on the thermoelectric conversion, we present the voltage enhancement ratios of the TEG systems with graphene-dispersed nanofluids as coolants for the cold side in Fig. 8. It can be observed in Fig. 8 that the enhancement ratio of the voltage decreases monotonously with the Reynolds number. With 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluid applied, the enhancement ratios of the voltage can reach 4.30%, 5.98%, 7.19%, and 8.81%, respectively, at the Reynolds number of 15.
Fig. 8. (color online) Enhancement ratio of the voltage of the TEG systems as a function of Reynolds number with different coolants.
When the electrical resistance of the output circuit is set, the output power has a quadratic relation to the voltage. In order to show the effect of the nanofluid coolants on the conversion from thermal energy to electrical energy of the TEG system, we further show the dependence of output power, P, with different cold side conditions on the flow rate of the coolant in Fig. 9. The variation tendency of P is similar to that of U shown in Fig. 7. For comparison to the case with distilled water as coolant, figure 10 depicts the output power enhancement ratios with graphene-dispersed nanofluids as the coolants for the cold side of the TEG systems. By using 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluids as coolants, the enhancement ratios of P are 8.79%, 12.32%, 14.90%, and 17.98%, respectively, at the Reynolds number of 15. These results clearly demonstrate that the thermoelectric conversion can be significantly enhanced by adjusting the heat transfer capacity of the cold side of a TEG system.
Fig. 10. (color online) Enhancement ratio of the output power of the TEG system.
As addressed above, the heat energy absorbed from the hot side of the TEG system converts into electrical energy partly and the remaining part is transferred to the heat sink through the cold side of the TEG system. When the heat transfer capacity of the coolant is enhanced by the increasing flow rate and the heat absorption capacity of the hot side is also enlarged at the same time, the conversion efficiency would be increased. The results shown in Fig. 11 are the evidence of this prediction. When the cold side of the TEG system is cooled by nanofluids instead of distilled water, the conversion efficiency is obviously increased (see Fig. 12). The conversion efficiency would be enhanced when the nanofluid with more graphene nanoplatelet added is used as the coolant for the cold side. The nanofluid can improve the heat transfer capacity of the cold side of the TEG systems effectively due to its good thermal properties. The conversion efficiency is increased by 5.15%, 7.14%, 8.55%, and 10.23% at most respectively with 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluids applied at a Reynolds number of about 15. Therefore, nanofluids have a strong influence on enhancing heat transfer, although the flow rate between the cold side and the heat sink should be tuned carefully to optimize the voltage, the output power, and the conversion efficiency.
Fig. 12. (color online) Enhancement ratio of the conversion efficiency of the TEG system as a function of Re with different coolants.
4. Conclusion
A three-dimensional and steady-state numerical model for simulating the heat transfer and the energy conversion of TEG systems were developed. Nanofluid coolants were used to optimize the cooling effect of the TEG systems. Our results showed that nanofluids included in the TEG systems could significantly increase the TEG efficiency. Obvious enhancements in the output voltage and electrical power of the TEG systems by nanofluid coolants have been achieved with 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene nanoplatelets added. The conversion efficiency has been increased by 5.15%, 7.14%, 8.55%, and 10.23% with 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluids at a Reynolds number near to 15. Moreover, the 0.025-wt%, 0.05-wt%, 0.075-wt%, and 0.1-wt% graphene-dispersed nanofluids increase the voltage and the output power by 4.30%, 5.98%, 7.19%, 8.81%, and 8.79%, 12.32%, 14.90%, 17.98% at a Reynolds number near to 15. It is clearly indicated that the heat transfer effect of the cold side has a strong influence on the output performance of the TEG system. Nanofluids can be used as a smart material working as a heat valve to control the flow of heat. Graphene-dispersed nanofluids for TEG system cooling could result in greater temperature difference and then lead to larger output voltage and conversion efficiency. Using nanofluid is an effective approach to enhance the heat transfer performance of the coolant and then the TEG system.
