† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61505175 and 61475134) and the Natural Science Foundation of Hebei Province, China (Grant Nos. F2017203110 and F2017203193).
Surface plasmon resonance induced tunable polarization filters based on nanoscale gold film-coated photonic crystal fibers were proposed and analyzed. The characteristics of the polarization filter were calculated by finite element method (FEM). The gold film was selectively coated on the inner wall of one cladding air hole which was located near the fiber core along the y-axis direction. When the phase of core fundamental mode and surface plasmon polaritons (SPPs) mode matches,the two modes couple with each other intensely. Numerical results show that the resonance wavelength and strength vary with fiber structural parameters and the index of the infilling liquid. The fiber parameters were optimized to achieve specific functions. Under the optimal structure, we realized a dual channel filter at the communication wavelength of 1.31 µm and 1.55 µm for y polarization direction and x polarization direction. Then a single channel polarized filter at the communication wavelength of 1.55 µm is also achieved by adjusting the refractive index of the infilling liquid. The proposed polarization filters realized dual channel filtering and single channel filtering simultaneously under the same structure for the first time to the best of our knowledge.
Photonic crystal fiber (PCF),[1,2] also known as the microstructure fiber, wraps light within microstructure of air holes that are arranged in a certain order in the transmission. In recent years, it has attracted widespread attention owing to some novel properties. The characteristics of high birefringence are good for the design of polarization components and can be generated by arranging the air holes asymmetrically. With the development of simulation and fabrication technology, the PCF of different structures being selectively infiltrated with functional materials provides a promising platform for novel photonic functional devices with the advantages of tunability, flexibility in design, all-in-fiber structure and integration, such as optical switches, filters, polarization splitter, modulators, dispersion compensators, and optical fiber sensors.[3–5]
Surface plasmon polaritons (SPPs)[6,7] are infrared or visible-frequency electromagnetic waves that propagate along a metal–dielectric interface. When the SPPs are stimulated by the incident light, the energy of the incident light can transfer to the surface of the gold film in the case of phase matching. This phenomenon is called surface plasmon resonance (SPR).[8] The transmission spectrum of the incident light appears as a dip when SPR happens.
Optical fiber polarizing devices[9–11] are essential components for optical sensors and communication systems. The traditional polarizers including sheet polarizer, prism polarizer, and brewster-angle polarizer have shortcomings such as high cost, high loss, mechanical instability and difficulties integrating with the optical communication networks or optical sensors,[12] while the surface plasmon resonance induced polarization filters can overcome the above disadvantages. In metal film coated PCFs, the light transmitted in the fiber-core can couple to SPPs as phase matching happens. So at the phase matching points, the fundamental modes appear as loss peaks which makes the PCFs have the potential to be in-fiber polarization filters. Zhang et al.[13] have shown selective coating in air holes of PCF via precipitation from a reduction reaction. Liu et al.[14] reported a tunable fiber polarization filter by filling different index liquids and gold wire into photonic crystal fiber. As for the selective filling, there are many techniques to achieve such as collapsing air-holes, injection-cleave techniques[15,16] and direct manual gluing.[17–20] Xue et al.[21] proposed an infiltrate PCF polarization filter based on SPR. The results exhibit that the resonance loss can reach 508 dB/cm for y polarization mode at the wavelength of 1311 nm and the full width half maximum (FWHM) is 20 nm. Hameed et al.[22] designed a tunable gold wire filled PCF polarization filter. The design has a central hole filled with a nematic liquid crystal to produce good adjustability with external electric field or temperature. Liu et al.[23] reported a nanoscale gold film coated PCF polarization filter for the range of 1.31, 1.48, and 1.55 μm. The shortcoming of it is that the authors have to change the size of the air hole coated with gold film to gain the polarization filtering at the three wavelengths.
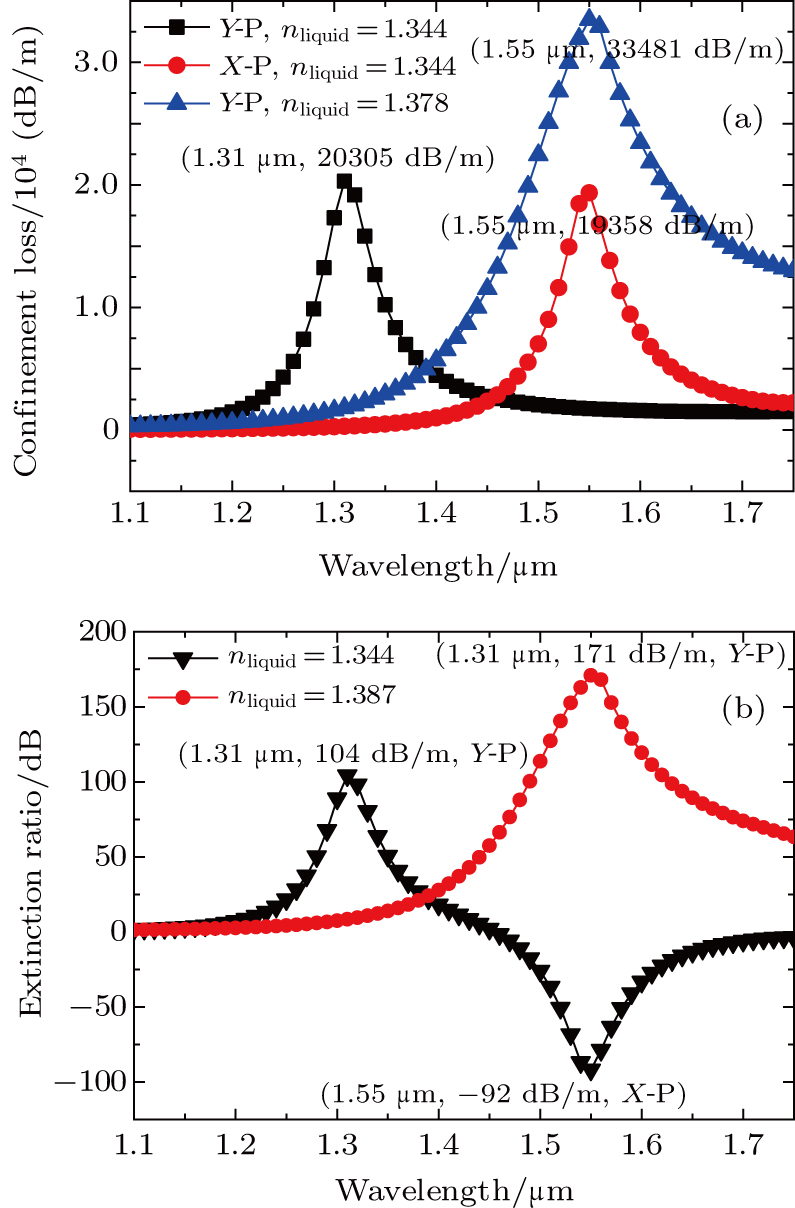
In this paper, we designed a tunable liquid-filled PCF polarization filter based on SPR with nanoscale gold film. It can realize dual channel polarization filtering at the communication wavelength of 1.31 μm and 1.55 μm in y and x polarization directions. We can also obtain a single channel filtering at the wavelength of 1.55 μm in the y polarization direction by adjusting the index of liquid without changing the structural parameters. The values of extinction ratio at the above wavelengths are 104, −92, and 171 dB respectively, which are better than those obtained in Ref. [23].
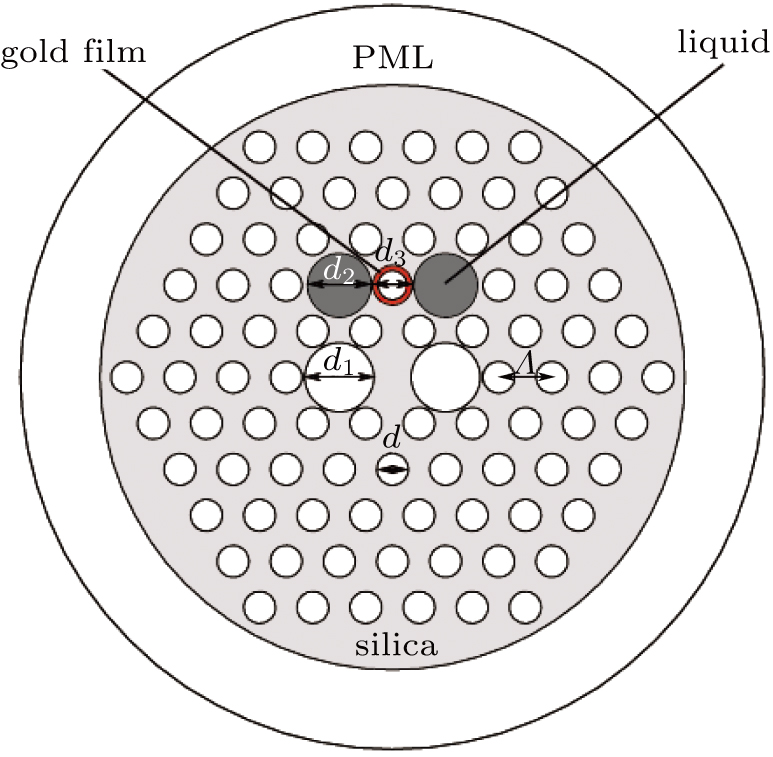
The structure of the designed PCF polarization filter is shown in Fig.
The mode birefringence of the PCFs can be expressed as
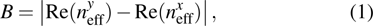 |
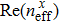
The background material is pure silica and the dispersion relation is calculated using the Sellmeier equation[24]
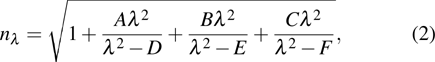 |
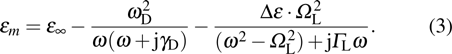 |
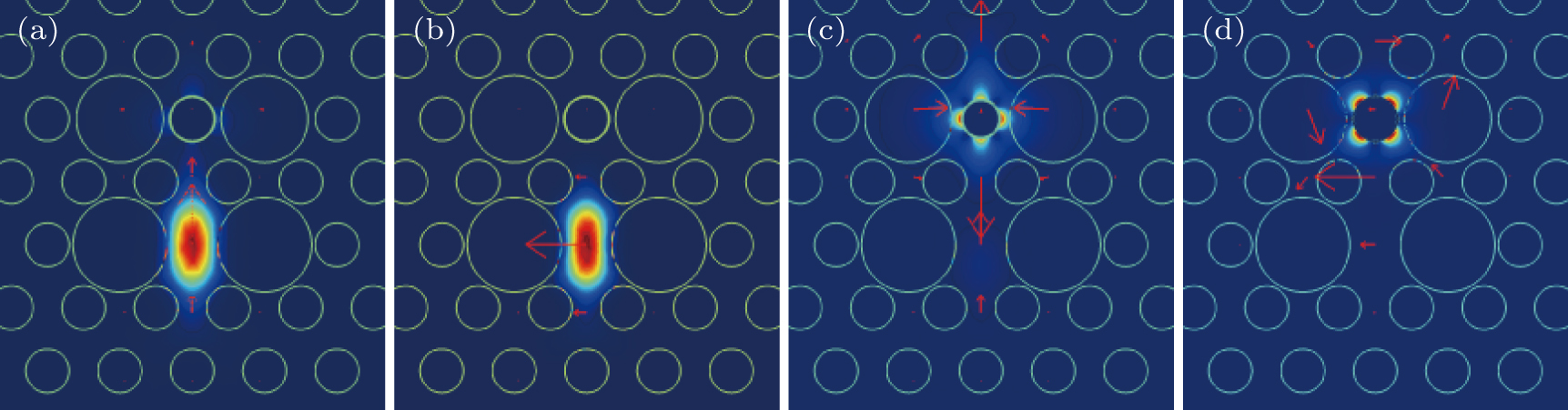
The electric field distributions of core fundamental modes in (a) the Y polarization direction, (b) the X polarization direction, and 2-nd SPP modes in (c) the Y polarization direction, and (d) the X polarization direction are shown in Fig.
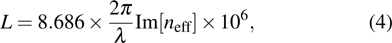 |
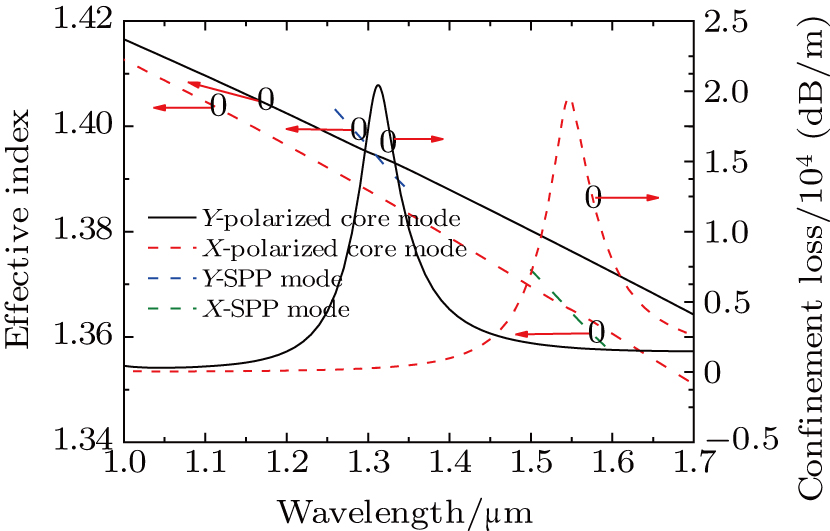
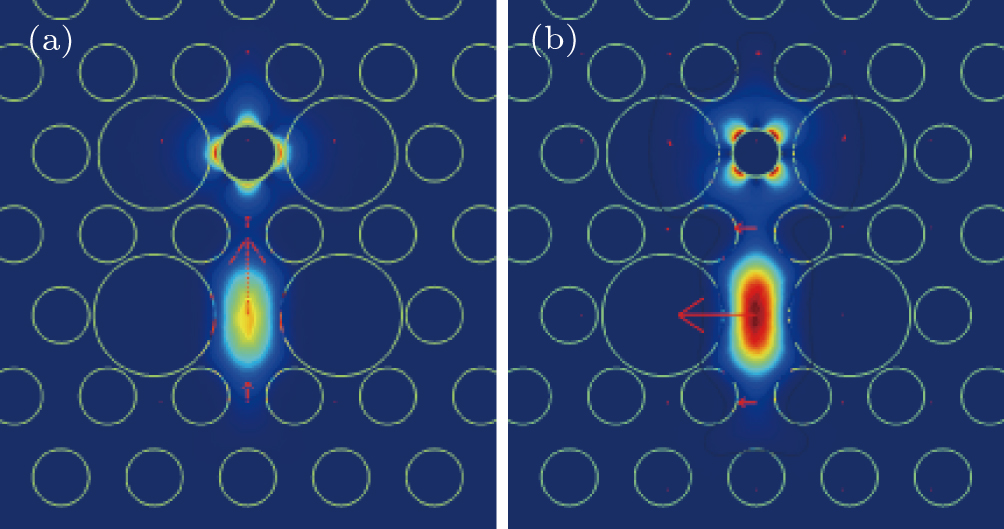
In Fig.
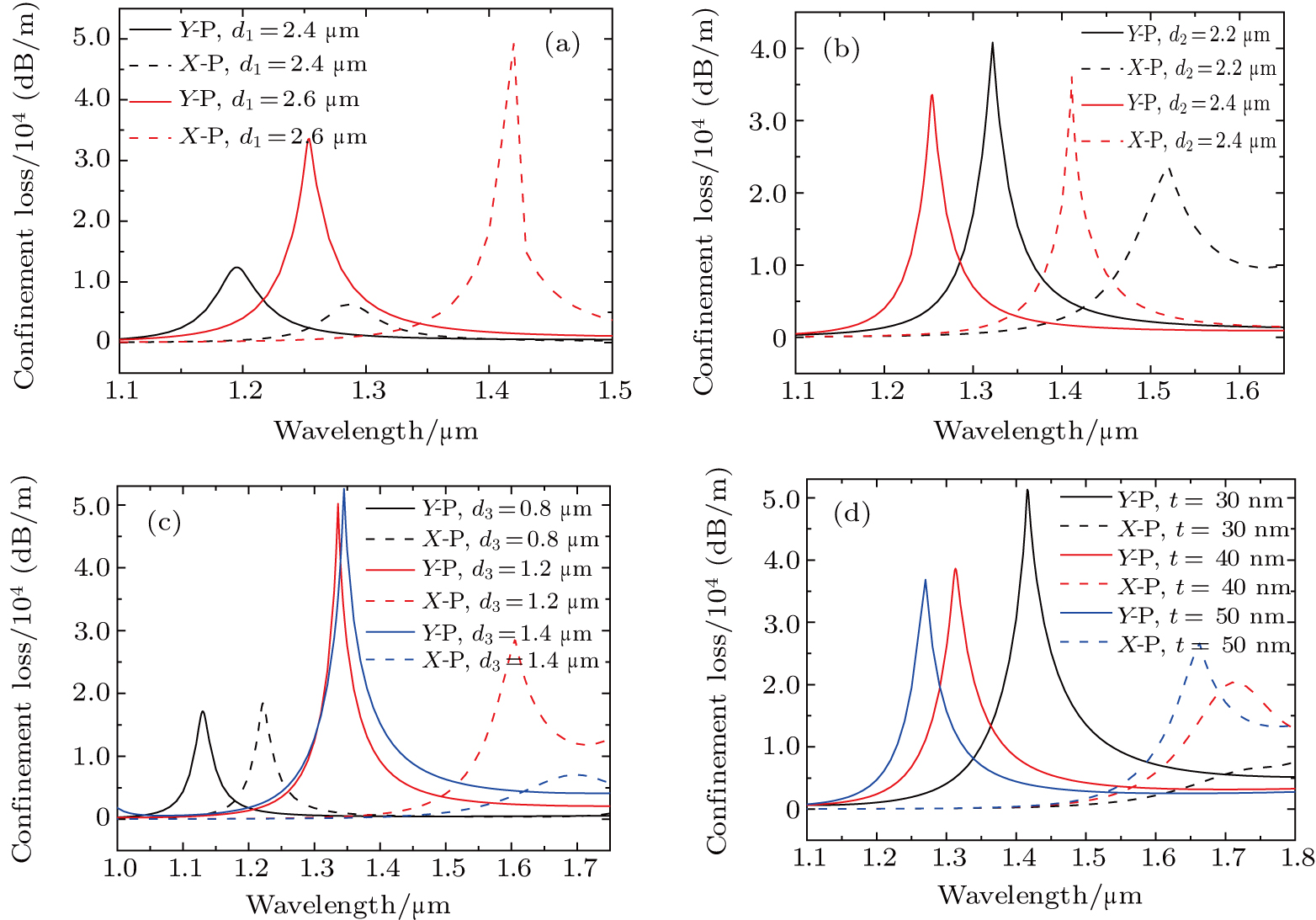
The effects of geometrical parameters of d1, d2, d3, and t on the filtering characteristics of the polarization filter are discussed below to acquire the optimal structure. The other structural parameters are set as d = 1.2 μm, Λ = 2 μm. The resonance loss dependence on the wavelength of λ in X-polarization direction and Y-polarization direction is shown in Fig.
The tunable liquid-filled PCF polarization filters based on SPR were designed. The gold film was coated on the wall of the cladding air hole near the fiber core along the y-axis direction. The two air holes on both sides of it are filled with liquid. We can change the index of the liquid to adjust the phase matching point. The FV-FEM with PMLs was introduced. The effects of structural parameters on the polarization characteristics of the polarization filter were analyzed. When the structural parameters were d1 = 2.6 μm, d2 = 2.4 μm, d3 = 1.2 μm, t = 30 nm, d = 1.2 μm and liquid index nliquid = 1.344, we obtained a dual channel filter at the communication wavelength of 1.31 and 1.55 μm for y polarization and x polarization. When the liquid index was 1.387, it filtered out the communication wavelength 1.55 μm in the y polarized direction. The structure can be further optimized for better performance, and all the analyses were beneficial to further studies on other fiber-based plasmon devices. Moreover, the fiber length is only 0.6 mm and it can be easily integrated into a compact instrument, which is useful for the miniaturization of an optical integrated communication system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] |