† Corresponding author. E-mail:
The vibration is one of the important factors affecting imaging quality of conventional remote sensing imaging because the relative motion between the imaging system and the target can result in the degradation of imaging quality. The influence of the vibration of the detector in the test path on reflective ghost imaging (RGI) is investigated theoretically and experimentally. We analyze the effects of the vibrating amplitude and velocity. The results demonstrate that the microvibrations of the bucket detector have almost no impact on the imaging resolution and signal-to-noise ratio (SNR) of RGI, i.e., the degradation of imaging quality caused by the vibration of the detector can be overcome to some extent. Our results can be helpful for remote sensing imaging.
The relative motion between the camera and the object imaged has always been one of the principal factors affecting the quality of conventional imaging. It can result in the degradation of imaging quality, even leading to the difficulty of identifying the imaging content. This unavoidable problem can be solved by shortening the exposure time and adopting the restoration algorithm of post-processing of the image.[1–3] However, these solutions either require very high imaging equipment, or need a long time to deal with. Some algorithms are difficult to achieve in practice. In order to achieve low-cost anti-motion blur imaging, we can consider the use of other imaging methods. As a non-local imaging method in recent decades, ghost imaging has been rapidly developed and widely concerned. According to the theoretical proposal of Klyshko,[4] Shih et al. first experimentally realized ghost imaging (GI) and ghost interference.[5] In 2001, Abouraddy et al. thought that quantum entanglement was a prerequisite for achieving distributed quantum imaging,[6] which set off an animated discussion. However, Bennink provided an experimental demonstration of ghost imaging by using a classical source in 2002.[7] Since then, the pseudo-thermal source is usually used to achieve ghost imaging.[8–10] The first experimental demonstration of two-photon correlated imaging with true thermal light[11] was reported in 2005. Wang et al. showed the macroscopic difference between quantum and classical coincidence imaging[12]. Lenless ghost imaging with thermal light was proposed in 2006.[13] Most lensless ghost imaging is conducted by using the transparent features of the object or with different transmission media.[14–16]
Differing from previous configurations, the first reflected ghost imaging experiment was realized by Meyers et al. and their experimental setup captured a ghost-image by counting the reflected photons from the surface of the target object.[17] Computational ghost imaging[18,19] can be realized with a single-pixel detector, which greatly simplified the system of ghost imaging. Erkmen described the applications of computational ghost imaging in remote sensing.[20] Gong and Han proposed a ghost imaging lidar via a sparsity constraints (GISC lidar) system and demonstrated that high-resolution imaging could be realized at a distance about the 1.0-km range[21] and that a three-dimensional (3D) GISC lidar system could be achieved with the GISC method.[22] The range accuracy of 3D ghost imaging ladar[23] and GI with broad distance[24] have been studied. In practice, it is quite common that the imaging target moves while the imaging system keeps relatively static. So the study of the ghost imaging of the moving target is very meaningful. Noted that the ghost imaging with moving target has been investigated in the literature.[25–30]
In some cases, such as air-to-ground detection, the vibration of the detector is inevitable because of the existence of atomospheric turbulence. In this paper, we present the experimental results about the influence of a shaking detector (bucket detector) on the quality of reflective ghost imaging (RGI). The effects of the vibrating velocity and amplitude are investigated. It is found that the resolution of RGI keeps unchanged when the bucket detector shakes slightly, while the corresponding result of direct imaging is affected greatly.
Figure 

According to the description of Gatti[32] and Cheng,[33] the second-order correlation function of intensity fluctuations between two detectors is
 |
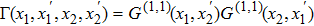
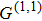
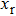

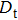
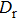
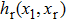
 |
In the test arm, the object consists of two reflected strips instead of a transmittive object. If the surface of the target is sufficiently smooth,[34] the object can be modeled by
 |
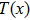
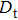
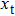
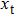
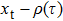
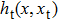
 |
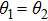
Following along the lines of our other work[35] and substituting Eqs. (
 |
In our experiment, a reflecting double-strip (two very thin reflected lines, lines width 


To highlight the difference between reflective ghost imaging with static and shaking detectors, we first implement static ghost imaging and conventional imaging experiments, and the corresponding results are illustrated in Fig. 


 | Fig. 2. The acquired image of the double reflective-strip from the two-arm imaging system, (a1) is obtained directly by  |
Then we analyze the effect from the change of the shaking amplitude of the bucket detector on imaging quality. Figure 







To perform a more accurate comparison, we calculate the signal-to-noise ratio (SNR) which was defined as Eq. (6) in Ref. [36]. The corresponding results are shown in Figs.
Next we focus on the effect of the shaking velocity of the bucket detector. Here we keep the experimental parameters (





In conclusion, we have investigated the influence of the detector’s vibration on the imaging quality of the reflective ghost imaging. Under different vibrating amplitudes and velocities of the test detector, the performance of the conventional imaging and the ghost imaging are quite different. The quality of the conventional imaging becomes worse with the increase of the shaking amplitude and velocity. However, the constructed ghost-image in RGI has almost no changes. That is to say, RGI can overcome the motion blur caused by the relative micro-motion between the test detector and the target, and gain a ghost-image with better quality.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |





