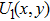Cite this Article
Luan Yin-Sen, Xu Bing, Yang Ping, Tang Guo-Mao. Wavefront analysis for plenoptic camera imaging. Chinese Physics B, 2017, 26(10): 104203  
Permissions
Wavefront analysis for plenoptic camera imaging
Luan Yin-Sen1, 2, 3, 4, Xu Bing1, 2, †, Yang Ping1, 2, Tang Guo-Mao1, 2
Key Laboratory on Adaptive Optics, Chinese Academy of Sciences, Chengdu 610209, China
Institute of Optics and Electronics, Chinese Academy of Sciences, Chengdu 610209, China
University of Chinese Academy of Sciences, Beijing 100049, China
College of Information Science and Engineering, Henan University of Technology, Zhengzhou 450001, China

 

† Corresponding author. E-mail: bing_xu_ioe@163.com

Abstract

The plenoptic camera is a single lens stereo camera which can retrieve the direction of light rays while detecting their intensity distribution. In this paper, to reveal more truths of plenoptic camera imaging, we present the wavefront analysis for the plenoptic camera imaging from the angle of physical optics but not from the ray tracing model of geometric optics. Specifically, the wavefront imaging model of a plenoptic camera is analyzed and simulated by scalar diffraction theory and the depth estimation is redescribed based on physical optics. We simulate a set of raw plenoptic images of an object scene, thereby validating the analysis and derivations and the difference between the imaging analysis methods based on geometric optics and physical optics are also shown in simulations.

PACS: 42.30.-d;42.30.Va;42.30.Tz;42.25.-p
Keyword:plenoptic camera;wavefront analysis;scalar diffraction theory
1. Introduction

A plenoptic camera consists of three parts: the main lens, microlens array, and image sensor. Compared with the standard camera, a microlens array is located in front of the image sensor in the plenoptic camera. Therefore, the plenoptic camera can retrieve the direction of light rays while detecting their intensity distribution, i.e., the plenoptic camera can record the light field emanating from the scene.[1–5] Specifically, from the geometrical optics, the complete seven-dimensional parameterization of the rays at any position and time is known as the plenoptic function.[6]

where λ is the wavelength, t is the time, is the position of the camera center, and is a point in the image. The dimensions of the plenoptic function can be reduced by imposing restrictions on the acquisition setup. Thus, we can omit t for a static scene and we can omit λ by considering separate red, green and blue images. A convenient parameterization, the Light Field or Lumigraph, assumes the light ray intensity is constant along its length, the cameras are restricted to the plane and define a light ray by the coordinates of its intersections with two parallel planes, i.e., the image plane and the camera plane . This leaves us with the four-dimensional parameterization:
The two-plane parameterization is a very natural fit for the light field inside the camera because each ray that contributes to a photograph passes through the lens aperture and terminates somewhere on the image sensor. In Fig. 1, the two-plane parameterization is shown and a single ray is shown passing through the lens aperture at as it refracts through the glass of the lens, and terminates at a position on the image sensor.[1,3,7]

Fig. 1. A 4D parameterization of the light field, the xy plane is the image plane and the plane is the principal plane of the lens. A single ray is shown passing through the lens aperture at , and terminates at position on the image sensor.

Generally, the plenoptic camera can be divided into two classes: the traditional plenoptic camera (Stanford plenoptic camera or plenoptic camera 1.0)and focused plenoptic camera (plenoptic camera 2.0).[1,3] Figure 2 depicts the traditional plenotpic camera imaging and the focused plenoptic camera imaging from the basic idea of geometrical optics.[5] In a focused plenoptic camera, it has a microlens array placed at distance b from the sensor, so that the microlens array is focused at the image plane of the main lens, at a distance a in front of the microlens array. In this configuration, the microlens array satisfies the lens equation and constructs a relay system with the main lens. The fundamental difference between the focused plenoptic camera and the Stanford plenoptic camera is that in the former, the micro-images are focused on the scene (through the relay system), while in the latter they are completely defocused with respect to the scene.

Fig. 2. Basic imaging models of Stanford plenoptic camera (a) and the focused plenoptic camera.

Contrary to previous research, in this paper, we adopt the physical optics to analyze the focused plenoptic camera imaging, which shows the wavefront transformation of the object in plenoptic imaging, equally, for the traditional plenoptic camera. The simulation results prove the derivations and analysis, which reveals more natures of plenoptic camera imaging from the angle of wave optics.

2. Wavefront analysis

In plenoptic camera imaging, the object scene is first captured by the main lens, and then the scene is imaged by the microlens array.[5] For simplicity, in the wavefront analysis, only the second imaging is considered. Besides, the object scene can be regarded as a set of point sources and the plane wave can be regarded as a spherical wave of infinite radius.[8] Without loss of generality, a point source on the object surface T is considered as an example in the following. Let S be the instantaneous position of a spherical monochromatic wavefront of radius r which proceeds from the point source P0. The time periodic factor ( is the temporal frequency and j is the imaginary unit) being omitted, the disturbance at a point on the wavefront may be represented by

where A is the amplitude at unit distance from the source, and , with λ being wave length.

The representation of S is a sphere:

so,
In Fig. 3, for the point source in front of microlens array, its wavefront S can be sliced and received by several microlenses, and each microlens samples the different parts of S, which is equivalent to multi-view imaging of one object point in geometrical optics. In addition, the number of microlens imaging for the point source is determined by the field of view of the main lens θ and the object distance l. Noting that the surface T in Fig. 3 is the image of the real object surface imaged by the main lens. Besides, the vectors , , and are normal vectors of wavefront S, which pass through the microlens centers.

Fig. 3. Wavefront sampling of image point and the wavefront is sliced and received by several microlenses.

In physical optics, the imaging system can be simulated by Collins equation or Fresnel diffraction. We use the latter to simulate the imaging of a microlens array. Firstly, as shown in Fig. 4, the wavefront is part of S and its complex amplitude is

where A0 is the amplitude at unit distance from P0
and is the center coordinate of the microlens at the plane z = 0. When the wavefront is sliced and imaged by different microlenses, the parameters r0, z and the phase are changed with different center coordinates of microlens which can be achieved with some calibration methods.[9] Subsequently, the values of complex amplitude in front of microlenses are different so that the images of the same point are different under different microlenses.

Fig. 4. Wavefront transformation of a microlens.

When the wavefront passes through the microlens array, the phase factor of disturbance will be tuned by a microlens, and the thin lens transformation for the disturbance is

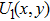
where f is the focus length of the microlens. So is
The disturbance on the image sensor can be calculated by Fresnel diffraction,[10]
where d is the distance between the plane z = 0 and the plane .

Finally, the intensity distribution of the image under the microlens is

where is the conjugate complex amplitude of .

Consequently, the transformed information of (part of wavefront S) is recorded by the image sensor. Therefore, different microlenses can sample different parts of wavefront S, and finally the wavefront S of point source is recorded by the microlens array. Furthermore, when the wavefronts of all point sources on the curved surface T are captured, the plenoptic image of the object scene is obtained.

For estimating the depth, as depicted in Fig. 3, the distance l is defined as the depth of point source . Since the depth of the point source is estimated as long as the sphere center is located, the estimating of depth can be treated as the calculating of the spherical center of wavefront. Firstly, we consider the normal vector of the spherical wavefront S, which can be obtained by taking a derivative of curve representation. Hence, the normal vector of a spherical wavefront at point Q is

Therefore, the normal vector of the wavefront at the center of microlens M1 is
where is the center of M1, which can be calculated through determining the physical parameters of microlens array.

Moreover, the normal vector of the wavefront at the center of microlens is

where is the image point of the point source, and its coordinates can be achieved by image feature location.

The vectors and are parallel due to the laws of lens transformation, so

Equally, for the microlens M2, the normal vectors and are parallel, so
The coordinates of the spherical center can be algebraically obtained by solving Eqs. (13) and (14), i.e., the depth of the point source can be estimated. Generally, in plenoptic imaging, the wavefront from one object point can be sliced and sampled by several microlneses, so the depth of the point can be optimally calculated with several equations like Eqs. (13) and (14). Closer inspection of Eqs. (13) and (14) reveals that the equations are a two-point form of a straight-line equation, and in fact, the sphere center , i.e., the space position of the point source is determined by the intersection between these space straight lines, which essentially coincides with the depth estimation method via triangulation summarized by Hartley and Sturm.[11] Equations (10)–(14) show that, in fact, the normal vectors of wavefront are the ray directions, which re-describes the depth estimation from the angle of wavefront analysis.

3. Simulations and comparisons

For the purpose of verification, the plenoptic imaging is simulated by scalar diffraction theory. For simplicity, in this simulation the microlens array consists of 10× 10 microlenses with focal length f = 1.8 mm, its arrangement is specified to be rectangular, and the wavelength λ = 632.8 nm. The raw plenoptic images of a circular ring (computer-generated imagery) with different values of object distance l are simulated, where the l is defined in Fig. 3. The circular ring is discretized into 256× 256 point sources, and each point source emits a regular spherical wavefront which is sliced and sampled by these 100 microlenses. When all point sources are captured, the raw plenoptic images are obtained.

Specifically, figure 5(a) is the picture of a circular ring and Figs. 5(b)–5(f) are raw plenoptic images corresponding to the values of object distance l of 1.2d, 1.4d, 1.6d, 2d, and 2.4d, respectively, where the l and d are defined in Fig. 3. Since the optimal focus plane of the microlens is located at l = 2d, figure 5(e) is sharp and other images are blurred more or less, and from the raw images in Figs. 5(b)–5(f) we can see that the circular ring is imaged more times with larger object distance, which coincides with the imaging law of a real plenoptic camera.[5] Note that in the simulation the amplitude of complex amplitude, i.e., the A in Eq. (3), is determined by the gray value of the object (Fig. 5(a)).

Fig. 5. (a) Image of a circular ring, ((b)–(f)) raw plenoptic images corresponding to the values of object distance l of 1.2d, 1.4d, 1.6d, 2d, and 2.4d, respectively.

To study the difference between the two analysis methods based geometric optics and physical optics, we also reproduce the plenoptic imaging from the angle of the ray tracing model and matrix optics. In this part, we refer to the researches of Andrew Lumsdaine and Todor Georgiev.[3] The light field or radiance is a density function where and are vectors that respectively represent the position and direction of a ray intersecting a plane transverse to the optical axis. The pair () is also denoted by a single vector . These coordinates are common in optics texts and relevant research papers.[3] For rays in three-dimensional space, and are two-dimensional vectors and is a four-dimensional vector. Without loss of generality, we adopt the convention of a two-dimensional q–p plane in this paper, in which case and are one-dimensional and is two-dimensional.

Rays are transformed due to translating a distance in the direction of the optical axis according to , which can be described as , where

Similarly, rays are transformed due to optical refraction of a lens with focal length f according to , which can be described as , where
Optical systems created from cascades of translation and lens elements are described by the product of the matrices representing individual elements. Specifically, in the simulation of pleoptic camera imaging, the transformation of rays refracted by the main lens and translating a distance before the microlens array can be described as , where F is the focus length of the main lens and the P is the distance between the main lens and the microlens array. After the rays pass through the space in front of the microlens array, which microlens will receive, the ray is determined. Then, the rays are refracted by the microlens and translate a distance between the microlens array and the image sensor, similarly, the transformation can be described as , where f is the focus length of microlens and the Q is the distance between the microlens array and the image sensor. When all rays emanating from the object are transformed by the plenoptic camera, the raw plenoptic image can be obtained.

For comparison, the plenoptic imaging of a horse (real image has a lot of textures) is simulated separately based on geometric optics and physical optics. In this simulation, the focal length of microlens array is f = 1.8 mm and the diameter of the microlens p = 1.28 mm. To save computation time, only 3× 3 microlenses are used in the microlens array. Figure 6(a) shows a picture of a horse, and the plenoptic imaging of the horse is simulated at the object distance l = 2d (l and d are defined in Fig. 3 and d = 2.7 mm), which is the optimal focus plane of the microlens. Specifically, figure 6(b) is achieved by geometric optics while figure 6(c) is achieved by physical optics. Figures 6(b) and 6(c) are almost the same, which verifies the analysis and simulation based on physical optics for plenoptic imaging.

Fig. 6. (a) Picture of a horse, (b) raw plenoptic images achieved by geometric optics, and (c) scalar diffraction theory (p = 1.28 mm).

In this simulation, the diameter of the microlens p is set to be 1.28 mm, but in a real plenoptic camera, a small diameter microlens () is often used in the microlens array. If the diameter is small enough that the diffraction effect of the microlens will blur the micro-image. Under this condition, the simulation based on geometric optics cannot show the real imaging of a plenoptic camera. As figure 7 shows, the point imaging simulation based geometric optics cannot reflect the real plenoptic imaging when the microlens diameter is small, but physical optics can.

Fig. 7. Point imaging simulations of microlens based geometric optics and physical optics with different microlens diameters (p = 1 mm, 0.5 mm, 0.3 mm, 0.2 mm, 0.15 mm, 0.1 mm).

Figure 8 shows another example of the plenoptic imaging. Compared with Fig. 6, the diameter of the microlens p is set to be 0.2 mm. From the figures, we can see that the simulation based on physical optics provides more real raw images of plenoptic imaging. Similarly, the more real plenoptic images of different scenes under different plenoptic camera parameters can be simulated, which will be an intuitive supplementary material in plenoptic camera design. What is more, when the simulated raw plenoptic image is achieved, it can be used to test the plenoptic image post-processing algorithms (such as depth estimation, refocusing) before the real plenoptic camera is built.

Fig. 8. (a) A picture of the horse, (b) the raw plenoptic image achieved by geometric optics(c) the raw plenoptic image achieved by scalar diffraction theory (p = 0.2 mm).

Besides, we use a point source to verify the depth estimation of the simulated raw plenoptic image. For example, when the distance between microlens array and the image point of point source P0 behind the main lens, i.e., l = 2.2d = 5.94 mm, the wavefront of a point source is sampled by the plenoptic camera as shown in Fig. 9, and figure 10(a) shows the raw plenoptic image of the point source. From the raw plenoptic image, we can see that P0 is imaged 9 times at the distance l = 5.94 mm. Therefore, the depth of can be estimated by locating the image points of under microlenses and solving equations like Eqs. (13) and (14) several times, and the estimated depth L = 5.96 mm which approximately equals the specified distance. This verifies the plenoptic camera imaging model based on physical optics and the depth estimation method. Moreover, figure 10(a) also presents the simulated point spread function of the plenoptic camera. Thus, the point spread function of the plenoptic camera can be achieved easily by physical optics.

Fig. 9. Point source imaged by plenoptic camera and standard cameras at different positions. Different view images are captured by the standard cameras at A, B, C, D, E, F.
Fig. 10. (a) Raw plenoptic image of , and (b) images of , which are imaged by standard cameras at positions A, B, C, D, E, F. For visibility, the images A, B, C, D are taken out of focus, all the images are printed on one figure, and the images E and F are moved up and down several pixels, respectively.

Furthermore, the different view images of can be simulated when the depth of is estimated as shown in Fig. 9, and the imaging of standard cameras at A, B, C, D, E, F are simulated based on Fresnel diffraction in physical optics. The result is shown in Fig. 10(b), for visibility, the images are taken out of focus slightly, all the images are printed on one figure, and the images E and F are moved up and down several pixels, respectively. Therefore, 6-view images of the point source P0 are achieved according to the standard cameras in Fig. 9. The images taken by cameras A and C are symmetric due to the positional relationship between cameras A, C and the point source, equally, B and D are also symmetric, which coincides with the imaging law of a standard camera. Similarly, when all point sources of the object surface T are located, the other view images under different camera parameters can be simulated.

4. Conclusions and future work

In this paper, we show that the plenoptic camera imaging can be characterized by wavefront analysis from the angle of physical optics. Specifically, the imaging model based physical optics of a microlens array is built, and the raw plenoptic images are simulated based on the scalar diffraction theory and geometric optics, which will be useful for plenoptic camera design. Moreover, the simulation can provide more real data to test the plenoptic image processing algorithm. Subsequently, the depth estimation is redescribed from the angle of wavefront analysis and multi-view images of the object scene are simulated when its depth is estimated.

Reference
[1] Ng R Levoy M Brédif M Duval G Horowitz M Hanrahan P 2005 Comput. Sci. Technical Report CSTR 2 11
[2] Levoy M Ng R Adams A Footer M Horowitz M 2006 ACM Trans. Graph. 25 924
[3] Lumsdaine A Georgiev T 2009 in Proceedings of Eurographics 5
[4] Dansereau D G Pizarro O Williams S B 2013 in IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 1027
[5] Perwass C Wietzke L 2012 Proc. SPIE 8291 829108
[6] Michael L Movshon J A 1991 Computational Models of Visual Processing Cambridge MIT Press 3
[7] Adelson E H Wang J Y A 1992 IEEE Trans. Pattern Anal. Mach. Intell. 14 99
[8] Huang L Bian Q Zhou C L Li T H Gong M L 2016 Chin. Phys. 25 070701
[9] Luan Y S He X Xu B Yang P Tang G M 2006 Opt. Eng. 55 043111
[10] Wu C Ko J Davis C C 2015 J. Opt. Soc. Am. 32 964
[11] Hartley R I Sturm P 1997 Comput. Vision Image Understanding 68 146