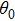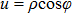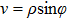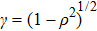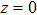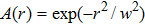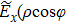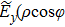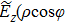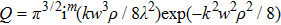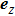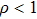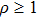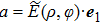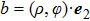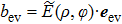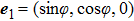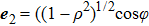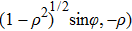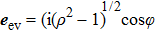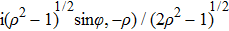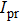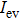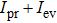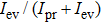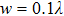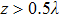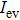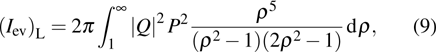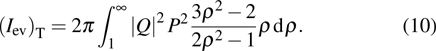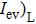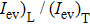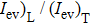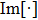Near-field characteristics of highly non-paraxial subwavelength optical fields with hybrid states of polarization
1. IntroductionThe propagation of non-paraxial electromagnetic beam has been extensively investigated in the last decade.[1–5] Several kinds of representations of an electromagnetic beam based on its angular plane-wave spectrum have been reported.[6–8] The contribution of evanescent waves is non-negligible and plays a key role in the near-field region.[1–6] Evanescent waves, which are also known as inhomogeneous waves,[1] have long been studied. They have been the subject of many studies and appeared in many branches of physics.[2] The evanescent waves of scalar beams with solely homogeneous polarization (e.g., linear, circular, or elliptical) in the cross-section of the field have been extensively studied[3–7] because of their novel properties and potential application in many areas, especially in the near-field region: nanophotonics, guided optics, internal reflection spectroscopy, and optical microscopy.[2] Merlin,[8] Grbic et al.[9] demonstrated the focusing of pure evanescent waves of a scalar optical field to generate a small focal spot beyond the diffraction limit. In contrast to most of the past researches based on spatially homogeneous polarization states such as linear, elliptical, and circular polarization, vector optical fields deal with spatially variant states of polarization (SoP) in the field cross-section. Recently, vector optical fields have aroused much interest in the linear and nonlinear optical fields because of their unique and novel properties and their potential applications, such as the generation of a different vector beam,[10–14] paraxial and nonparaxial propagation,[15–18] focusing a radially polarized beam to minimize the spot size,[19–23] and the self-focusing dynamics of a vector beam.[24,25] More recently, the evanescent waves of radially and azimuthally polarized and higher-order vector optical fields with locally linear polarization have been demonstrated.[26–29] The properties of a vectorial structure of an electromagnetic beam are well-known to play an important role in corresponding fields and applications such as propagation, beam control, and the excitation of surface plasmon polaritons (SPPs).[30,31] In a nanostructured material, only the component of the incident light that is polarized perpendicularly to either groove- or ridge–like scattering elements (e.g. gratings) or to the metal surface itself (e.g. prism-based schemes) can be coupled into SPPs. For an optical field with hybrid SoP (i.e., there are simultaneously linear, circular, and elliptical polarizations in the field cross-section), novel properties and potential applications have emerged owing to the existence of hybrid SoPs, especially their longitudinal components in a nano/micro-structure material.[32–34] Nonetheless, the near-field characteristics of an optical field with a hybrid SoP, especially the dynamic manipulation of the evanescent wave part, are scarcely known and the exploration of them is still in its infancy.
In this paper, we examine the evanescent wave of a vector optical field with a hybrid SoP in the cross-section of the field. The angular spectrum method,[22–25] which gives a rigorous solution to the Maxwell equations, is employed to separate the contributions of propagating and evanescent waves. The formalism is presented and discussed. The propagating and evanescent waves, which are expressed in terms of the non-paraxial vector optical field, are split into transverse and longitudinal components. The analytical expressions are derived and discussed. The spatial shapes of these components and the ratios between their respective contributions are numerically obtained. The intensities of the longitudinal component of the evanescent and propagating waves of a cylindrical vector optical field (with a hybrid SoP) are investigated each as a function of the propagation distance in the near-field region. The intensity distributions of the vector optical fields in the near-field region are found to strongly depend on the spatial distribution of the SoP in the cross-section of the field. In particular, the shapes of the intensity distributions of the longitudinal components are different from those of the transverse components, and it is sensitive to the spatial distribution of the SoP in the field cross-section. This is because of the contributions of different polarization components of a vector field to the evanescent wave. The longitudinal components of the evanescent term dominate the near-field, which gives rise to a variety of shapes in the field and the spin angular momentum (SAM) flux density distributions. Since many applications are related to reshaping the laser beam, the ability to modify the intensity profiles and the spin angular momentum flux density distributions by tailoring the SoP distribution may lead to the creations of more image spaces for applications in superresolution, nanofabrication, and plasmonic beaming. This work may provide useful information about manipulating the vector structure of a cylindrical optical field in the near-field by choosing appropriate SoPs in the field cross-section.
2. FormalismWe consider the propagation dynamics of a vector field with a hybrid SoP when using the cylindrical coordinate system. For this coordinate system, the z-axis is taken to be the propagation axis. A cylindrical vector optical field with a hybrid SoP in the cross-section of the field is expressed as[13]
where
and
denote the polar radius and azimuthal angle, respectively, of the polar coordinate system.
m is the number of the topological charges, and
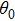
is the initial phase,
and
are the unit vectors in the
x and
y directions, respectively. Equation (
1) indicates a hybrid-polarized vector field with linear, circular and elliptical polarizations that are located at different positions in the cross-section of the field. For a locally linear polarization in the field cross-section, the imaginary sign ‘i’ on the right-hand side of Eq. (
1) should be cancelled.
[17–21] Figure
1 shows the corresponding hybrid SoP distributions in the cross-section of the initial field with
m = 1 and
m = 2. The white arrows indicate the directions of the polarization.
The transverse components of the vector angular spectrum 
, 
) and 
, 
) of the initial field are given by using Fourier transforms[35,36]
where
k is the wavenumber.
ρ and
φ represent variables that are related to the transverse Fourier-transform, i.e.,
u,
v, and
γ. Here,
,
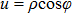
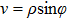
, and
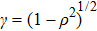
. For a hybrid-polarized optical field as given in Eq. (
1), in the source plane
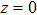
with the Gaussian distribution
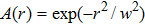
, where
w is the beam width, the transverse components of the angular spectrum
,
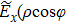
) and
,
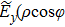
) can be obtained from the integrals in Eq. (
2). The
z component of the angular spectrum is
,
,
,
.
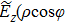
[26–29,34] Therefore, the angular spectrum of the vector beam is described as follows:
where
and
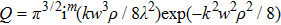
. I
denotes the Bessel function of the second kind, and
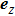
is the unit vector in the
z direction. The electric field component of the cylindrical vector optical field in the
z plane can be represented as
When
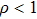
, equation (
4) describes the propagating waves
Epr. On the other hand, it gives the evanescent waves
when
.
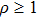
3. Contribution of the longitudinal component of evanescent wave to vector optical field with hybrid SoP in the near-field regionIn order to compare the contributions of the propagating and evanescent waves associated with the cylindrical vector field, the plane-integrated intensity (squared modulus) of the propagating field 
and evanescent field 
[25–29] are calculated. 
and 
are expressed as follows:
where
,
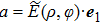
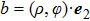
, and
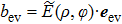
. Here
,
,
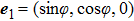
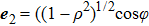
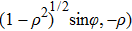
, and
,
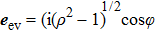
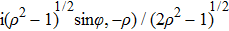
. Integrating
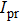
and
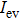
over
φ leads to the following single-variable
ρ integrals:
which can be solved by performing numerical integration over
ρ. The ratio of the evanescent intensity
to the total intensity of propagating and evanescent intensities
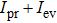
is introduced here to describe the relative weight factor of evanescent wave. The ratio of the evanescent wave component to the total field is shown in Fig.
2(a), whereas the ratio of the longitudinal component of the evanescent wave to the propagating wave is given in Fig.
2(b). Figure
2(a) illustrates the
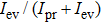
ratios each as a function of the propagation distance
z for a highly non-paraxial case of
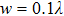
for different values of the number of topological charges
m. The evanescent field clearly dominates the optical field, particularly near the source plane
z = 0. For
,
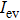
drastically decreases with propagation distance increasing. As the propagation distance further increases above
,
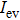
continues to decay and approaches to zero. Thus, the contribution of evanescent wave can be neglected when
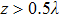
. As the number of the topological charge
m increases,
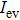
increases as shown in Fig.
2(a). This is because the field distribution broadens and extends from the beam centre as the number of the topological charge increases.
For the case of the paraxial condition, the longitudinal component of the evanescent wave can be ignored. In this high non-paraxial case (
), however, the longitudinal component of the evanescent wave cannot be neglected. In the following discussion, we focus on the relative weights of the transverse and longitudinal components of the evanescent wave, particularly for a high non-paraxial case (
). This is because the evanescent wave component is the dominant component in the near-field. Here the case of 
is valid for any other beam waist[6,7,25] even though the relative weights of the components of evanescent and propagating waves vary with beam waist as shown in Eqs. (4)–(6) and Fig. 2. The relative contribution of the transverse and longitudinal components of the evanescent wave can be examined by examining the (
ratio. Here, (
and (
denote the plane-integrated intensities of the longitudinal and transverse parts, respectively, of the evanescent wave 
. They are described by
 | |
 | |
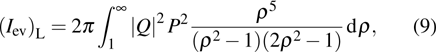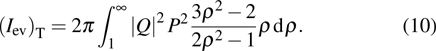As the longitudinal and transverse components of
are expressed in the plane-wave spectrum, the Parseval theorem
[28] indicates that (
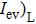
and (
are constant during propagation. Therefore, the (
ratio of the initial plane is sufficient to examine the contribution of the transverse component. Figure
2(b) shows the variations of (
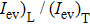
ratio with waist size
w of an optical field. It is found that the (
ratio increases with
w increasing and it approaches to a saturated value at a certain
w. As the polarization topological charge number
m increases, (
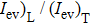
decreases, and the saturated value corresponds to
m shifts to a higher
w.
The contribution of the longitudinal component to the total field distribution in the near-field region of a vector field cannot be neglected. Therefore, we further examine the propagation properties of the vectorial structure to gain an insight into the behavior of the evanescent wave. The propagation behavior of the evanescent wave of a vector field with a hybrid SoP is analyzed by observing the evolutions of the field distributions, especially the longitudinal component. Figure 3 shows the intensity distributions of the longitudinal and transverse components for both the propagating and evanescent waves. As the number of the topological charge m increases, the distributions of the longitudinal and transverse components of the evanescent and propagating waves stretch out in the cross-section of the field. On the other hand, there are more longitudinal components that expand to the neighbouring region than the transverse components with increasing m as shown in Figs. 3 and 4. This is because the central field decreases with increasing w. Thus, the (
ratio decreases with increasing w, which results in the plot inflecting after 
when m = 1 in Fig. 2(b). However, as discussed above, with increasing topological charge m, the saturated value shifts to a higher w as shown in Fig. 2(b). For the evanescent wave, the reshaped intensity distributions of the longitudinal components are similiar to those of the propagating wave components. In addition, the evanescent wave has a smaller spatial size than the propagating wave. Interestingly, the longitudinal components of the reshaped intensity distributions are different from those of their corresponding transverse components.
The last column of Fig. 3 illustrates the centres of the longitudinal component for both the propagating and evanescent wave components of a radially polarized beam. The intensity distribution profile of the propagating wave is similar to that of the radially polarized sharper focusing beam on a subwavelength scale.[19,20] Figure 3 shows that the SoP distributions in the field cross-section result in the reshaping of the intensity distributions of the longitudinal components. Figure 4 shows the comparisons of the total longitudinal components of the propagating and evanescent wave terms with the total field (i.e., all components of the propagating wave and evanescent wave terms). The evanescent waves are found to dominate the near-field and be sensitive to the number of the polarization topological charge m and the distribution of SoP in the field cross-section. In the near-field region, the longitudinal components are the dominant components and play an important role in governing the shapes of field distributions. The reshaping of the intensity distributions of the longitudinal components is attributed to the SoP distribution in the field cross-section. As the distributions of the x and y components determine the distribution of the longitudinal components in the near field, a coherent superposition of the longitudinal components leads to the different longitudinal distributions in the near field as shown in Figs. 3 and 4. Such a vector structure of the optical field especially the longitudinal component can offer many applications such as the flexible manipulation of the optical field on a nanoscale by purposely choosing the initial SoP.
4. Vectorial structure of the optical spin angular momentum flux in near fieldUnder a highly nonparaxial condition, neither the evolution nor the distribution of the SoP of the vector beam in the near field can be described in a two-dimensional plane. In particular, the distribution of the circular polarization associated with the optical SAM is an important phenomenon due to the fundamental interest and its potential applications ranging from optical trapping to quantum information. Here we give vectorial descriptions of the optical SAM flux densities of x, y, and z components in the near field. The corresponding optical SAM flux density distributions of the optical field in the x, y, and z directions can be given by[36]
where
Sx,
Sy, and
Sz are the
x,
y, and
z components of the optical SAM flux density,
ε0 is the permittivity in a vacuum,
ω is the angular frequency,
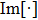
mean taking the imagery part and the asterisk denotes complex conjugation. Figure
5 shows the distributions of
x,
y, and
z components of the SAM flux density when
, hereafter the values of the SAM flux density are normalized to the peak value in the source plane
z = 0, and the positive and negative SAM flux denote the opposite circular polarizations (i.e., left and right circular polarization). Under the paraxial condition, the optical angular momentum flux can be considered as propagating along the
z direction and the transverse components can be ignored. Under the highly non-paraixal circumstance, however, the longitudinal component plays an important role and results in the occurrence of the transverse components of the SAM flux in the near field of the vector field. As can be seen from Eq. (
4), the phase differences among the
x,
y, and
z components are closely related to azimuthal angle
θ and topological charge
m. In particular, the distributions of the phases of
x and
y components and the distribution of the optical SAM of the
z component are similar to those in the paraxial case as shown in Fig.
5. However, the SAM flux density distributions of the transverse components which result from the longitudinal component are more interesting. The
x component and the
y component of the SAM flux density distribution are similar to each other because the vector optical field is cylindrically symmetric. However, the transverse components (
x component and
y component) of the SAM flux density distribution are different from those of the longitudinal component as shown in Fig.
5.
The transverse component of the SAM flux density is greater than the z component when 
. The component decreases rapidly with increasing propagating distance. The different distributions of the transverse component of the SAM flux density as shown in Fig. 5 arise from the variation of the longitudinal components as shown in Figs. 3 and 4. Since the micro-particle manipulation depends on optical angular momentum distribution, the three-dimensional vector structure of the optical angular momentum flux distribution may provide a more flexible manipulation of the micro-particle.
5. Conclusions and perspectivesThe near-field contributions of the transverse and longitudinal components of a vector optical field with a hybrid SoP are analyzed in detail. Physical images of the longitudinal components of evanescent waves are illustrated and compared with the transverse components from the vectorial structure. The contribution of the evanescent wave to the vector optical field is numerically analyzed and discussed. The relative intensity of the evanescent wave is found to increase with the number of the topological charge. As the propagation distance increases, the relative intensity of the evanescent wave decreases. The intensity profiles of the transverse components of evanescent waves are similar to those of the propagating waves, but the spatial sizes of the evanescent waves are smaller than those of the propagating waves. However, the spatial shapes of the intensity distributions of the longitudinal components are different from those of the transverse components, and they are more sensitive to the number of polarization topological charges. The distribution of the SoP in the field cross-section reshapes the intensity distribution of the longitudinal component. The longitudinal component of the evanescent wave dominates the near-field region to reshape the three-dimemsional vectorial structure of the optical field and the optical SAM flux density distribution. This study reveals that the ability to manipulate the longitudinal component distribution by controlling the SoP distributions, may lead to more image spaces for potential applications in superresolution, nanofabrication, micro-particle manipulation, and plasmonic beaming on a nanometre scale.
