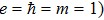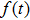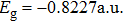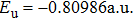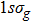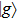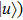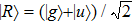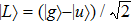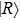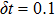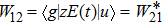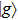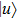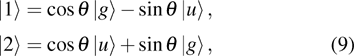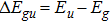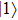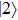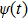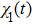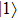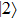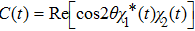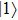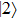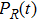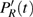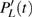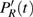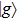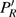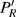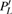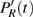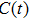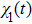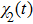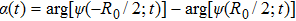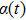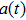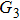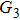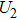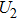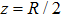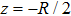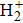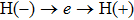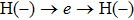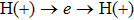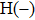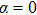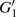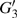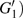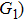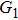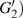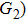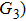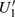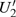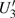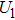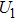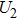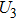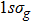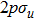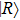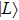2. Theoretical methodAll the calculations were performed for the 1D fixed-nuclei model of  , which exposed to a linearly polarized laser field, by using the parallel quantum wave-packet computer code LZH-DICP.[34,35] In the dipole approximation and the length gauge, the corresponding time-dependent Schrödinger equation is
, which exposed to a linearly polarized laser field, by using the parallel quantum wave-packet computer code LZH-DICP.[34,35] In the dipole approximation and the length gauge, the corresponding time-dependent Schrödinger equation is
When we consider the linearly polarized laser field along the molecular axis, the Hamiltonian of this system (
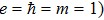
is given by
where
denotes the electronic kinetic-energy operator,

is the proton mass, and
z is the electronic coordinate with respect to the center of mass of the two protons. The soft-core Coulomb potential is expressed as
where
R is the internuclear distance of the molecular ion.
[36] The external interaction between the laser field and the molecule is given by
The electric field of the laser pulse is assumed to have the following form:
where
ω0 is the angular frequency and
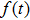
is the envelope function in the following form:
where
T is the pulse duration and
E0 is the peak strength.
Equation (1) is solved numerically by using the standard second-order split-operator method,[37,38]
where
T is the kinetic energy operator as in Eq. (
2), and
V is the interaction potential taking all the potential energy of the system plus a purely imaginary term to produce an absorbing boundary. In this study, we set
R = 7 a.u. The ground and the first excited state energies of this model are
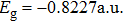
and
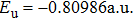
, respectively. The eigenstates
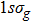
and

(denoted as
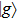
and
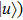
are almost degenerate and well isolated from the higher-lying excited electronic states. As shown in Fig.
1, the two lowest-lying states have opposite parities and their superpositions form two localized states
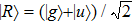
and
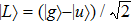
,
[39,40] where
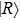
and

represent the electron wavepacket that is localized at the right and left protons, respectively. During the interaction with laser pulse, the

and
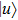
mix and thus the electron density oscillates between the two protons. The time step of the wave function propagation is set to be
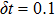
a.u.
3. Results and discussionFigure 2 presents the HHG spectra of  initially in its ground state and the first excited state with internucler distance R = 7 a.u., driven by a 10-cycle full-width infrared laser pulse with wavelength λ = 1400 nm and peak intensity
initially in its ground state and the first excited state with internucler distance R = 7 a.u., driven by a 10-cycle full-width infrared laser pulse with wavelength λ = 1400 nm and peak intensity  . At first glance, the two spectra show common feature: the plateaus span a broad bandwidth and exhibit almost constant intensity, and then drop steeply at the cutoff. Moreover, considerable suppressions, named interference minima, on the plateau are also observed in both cases. However, we note that the positions of the minima in the two spectra are different.
. At first glance, the two spectra show common feature: the plateaus span a broad bandwidth and exhibit almost constant intensity, and then drop steeply at the cutoff. Moreover, considerable suppressions, named interference minima, on the plateau are also observed in both cases. However, we note that the positions of the minima in the two spectra are different.
Due to the strong coupling between  and
and  in the radiative interaction, we study the underlying mechanisms for the interference minima based on the two-state model. We write the Hamiltonian of the two-state model as[41]
in the radiative interaction, we study the underlying mechanisms for the interference minima based on the two-state model. We write the Hamiltonian of the two-state model as[41]
where
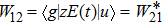
is the laser-molecule coupling,
Eg and
Eu are the eigenvalues of the
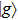
and
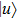
. The resulting eigenfunctions are given by
where
with the BO energy separation
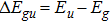
. The eigenvalues are
The two eigenfunctions
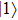
and
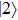
are called “phase-adiabatic” states.
Using the two-phase-adiabatic state model, the total wave function is expressed as
where the time-dependent wave function
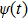
is obtained from Eq. (
7),
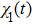
and

are the time-dependent coefficients associated with
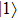
and
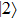
.
By projecting the wave function  onto the two localized states
onto the two localized states  and
and  , we obtain the expressions for the local populations at the respective protons as follows:
, we obtain the expressions for the local populations at the respective protons as follows:
where
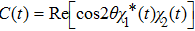
represents the interference between
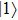
and
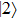
. To examine the validity of the
PR and
PL based on the two phase-adiabatic states model, we calculate the time-dependent populations of the wavepacket localized on the left and right protons as follows:
The time-dependent local populations
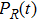
,
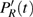
, and
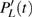
in the ground state case are presented in Fig.
3(a). From this figure, we note that
and

are not equal, which is not unexpected because in the expression of the

only the two lowest-lying states
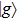
and

are counted and the higher-lying excited electronic states are not taken into account. Another feature shown from the figure is that the electron motion between the two protons does not always follow the laser-electron interaction. For example, at
t = 819 a.u. ∼916 a.u., the oscillating laser electric field

is negative. According to the semi-classical three-step model, the electric field force will push the electron into the

direction and the local population
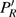
will gradually increase. Nevertheless, at certain times, we observe
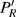
decreasing and
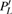
increasing at the same time, which means that at these times the electron transfers from the right well at
z = 3.5 a.u. to left well at
z = −3.5 a.u. The interwell electron transfer was reported first in Ref. [
41] and they attributed the interwell electron transfer to the interference between the two phase-adiabatic states. He
et al. also reported this classically forbidden motion of electron in dissociating
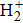
and named the motion the counter-intuitive motion.
[42] Figures
3(b) and
3(c) show the local population
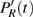
and the interference
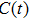
between the two phase-adiabatic states in the ground state case (
G case) and in the first excited state case (
U case), respectively. We find that the counter-intuitive motions of electron keep in step with the interference term in both cases, but these motions occur at different instants. According to the two-state model, we can deduce that the interference term depends not only on the electric field but also on the initial state. Different initial states lead to different coefficients
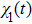
and
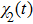
. Therefore, we attribute the different counter-intuitive motions of electron to the different interferences between the two phase-adiabatic states for the present parameters. References [
9] and [
14] have reported that the counter-intuitive motions of electron are closely related to the evolving phase difference
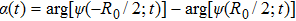
. The value of the phase difference
α ranges from

to
π. In Figs.
3(d) and
3(e), the time-dependent phase difference
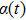
ʼs in the
G case and
U case are presented. By comparing the phase differences (Figs.
3(d) and
3(e)) with the local populations (Figs.
3(b) and
3(c)), we note that the counter-intuitive motion of the electron occurs when the phase difference passes through
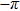
(or
π), and at moment when the electron is most located on the counter-intuitive side of the molecule,
α = 0. Compared with the events in the
G case, the counter-intuitive events occur at different moments in the
U case. This is maybe the reason why the positions of the minima are different in the two cases.
In order to verify the viewpoint, we perform the time-frequency analysis by means of the wavelet transform,[40]
where
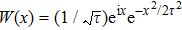
is the complex Morlet wavelet and
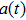
is the time-dependent dipole acceleration of the electron. Figures
4(a) and
4(b) show the time-frequency distributions corresponding to the
G case and
U case, respectively. We focus on the ionization times between 819 a.u. and 916 a.u. In the
G case, in each half cycle, there are two suppressed harmonic emissions denoted as
G1 and
G2 on the short quantum path, which match the spectral positions of the minima presented in Fig.
2. There is also one suppressed harmonic emission labeled
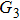
on the long quantum path. However, the corresponding harmonics of
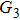
are not obviously linked to the spectrum minimum because the intensity of the long quantum path is much weaker than the short quantum path in this harmonic region, which can be seen from Fig.
4(a). In the
U case, there are two obvious suppressed harmonic emissions denoted as
U1 and
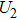
in each half cycle, but only the suppressed harmonic emission
U1 contributes predominantly to HHG minimum and the suppressed harmonic emission denoted as
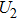
is not observed in the spectrum due to the same reason as the case of
G3. In order to in depth understand the mechanism of the suppressed harmonic emission, we investigate the classical electron dynamics by solving Newton’s equation of motion for an electron in the laser field described in Eq. (
5). The electron is assumed to be a negative point charge, and is released from one of the protons of the molecule with

throughout the ionization interval. Assuming that the recombination happens at the instances when
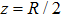
or
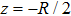
, each classical trajectory links a unique pair of ionization and recombination times [cf. Fig.
4(c)]. For the
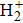
, there are four ionization-recombination channels in molecular HHG, i.e.,
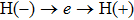
,
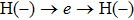
,

, and
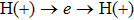
, where
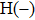
represents the proton located at
z = −3.5 and H(+) represents the proton located at
z = 3.5. The ionization and recombination times of the four channels are presented in Fig.
4(c). To characterize the interference dynamics, figures
4(d) and
4(e) present the variations of the phase difference
α at the time of ionization in the
G case and in the
U case, respectively. In the
G case, during the ionization times of 819 a.u.–916 a.u., there are three instants at which
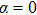
denoted as
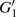
,

, and
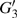
shown in Fig.
4(d). As shown in Fig.
4(c), the electron ionized from H(−) around 849 a.u. (
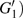
is accelerated by the

field, and then recombines with H(+) and emits the 39th–40th harmonics around 856 a.u.–866 a.u. (
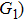
which corresponds to the suppressed harmonic emission
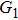
in Fig.
4(a). The electron ionized from H(+) around 887 a.u. (
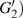
recombines with H(−) and emits the 80th–85th harmonics around 983 a.u. (
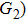
and this position is consistent with the suppressed harmonic emission
G2 shown in Fig.
4(a). The electron ionized around 868.5 a.u. (

recombines with one of the protons and emits about the 50th harmonic around 1040 a.u. (
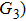
corresponding to the suppressed harmonic emission

shown in Fig.
4(a). In the
U case, there are also three instants at which
α = 0, and they are marked in the Fig.
4(c) as
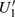
,
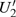
, and
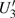
, respectively. The corresponding recombination times are also marked as
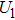
,

, and

in the Fig.
4(a) and Fig.
4(c), respectively. The electron ionized from H(+) or H(−) around 900 a.u. recombines with one of the protons and emits the 60th harmonics around 972 a.u. which is in accordance with the suppressed harmonic emission
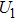
shown in Fig.
4(b). At the instants of
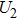
and
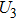
, the suppressed harmonic emissions are manifest in the time-frequency map [cf., Fig.
4(b)], but they are not obviously linked to the spectrum minima due to the weaker intensity of the corresponding quantum paths. Therefore the suppressed harmonic emission is related to the moment of the counter-intuitive motion of electron and the mechanism of the HHG minimum is the consequence of the interference between the two phase-adiabatic states at the ionization time.