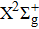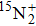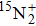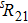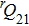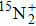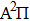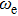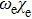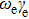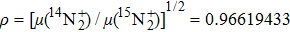A portion of the observed spectra and the corresponding assignments of the (2, 0) band of the  –
– system of
system of  are shown in Fig. 1. The observed line shape of a single transition is the second derivative of a Gaussian type. In the present work, the spectra of
are shown in Fig. 1. The observed line shape of a single transition is the second derivative of a Gaussian type. In the present work, the spectra of 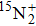 in the range of 12294.0 cm−1–12731.2 cm−1 were recorded. However, there are gaps in the spectra in the range of 12342.8 cm−1–12406.1 cm−1 and 12583 cm−1–12600 cm−1 due to the fluctuation of the output energy of our laser.
in the range of 12294.0 cm−1–12731.2 cm−1 were recorded. However, there are gaps in the spectra in the range of 12342.8 cm−1–12406.1 cm−1 and 12583 cm−1–12600 cm−1 due to the fluctuation of the output energy of our laser.
3.1. Rotational analysisThe ground state,  , of
, of 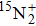 belongs to the Hund’s case (b). The levels with a given value of the rotational quantum number N are split into two components, F1 (
belongs to the Hund’s case (b). The levels with a given value of the rotational quantum number N are split into two components, F1 ( ) and F2 (
) and F2 ( ), due to the electron spin-rotation coupling. The parities of the rovibronic functions are given following the definitions of Brown and Carrington.[15] The excited state,
), due to the electron spin-rotation coupling. The parities of the rovibronic functions are given following the definitions of Brown and Carrington.[15] The excited state,  , obeys the Hund’s case (a) at low J values. Each
, obeys the Hund’s case (a) at low J values. Each  is split into two components:
is split into two components:  and
and  . The
. The  energy level higher than that of the
energy level higher than that of the  due to the negative coupling constant Av. For each
due to the negative coupling constant Av. For each  , a certain J level will split into two sublevels with inverse parities due to the
, a certain J level will split into two sublevels with inverse parities due to the  -doubling.
-doubling.
In the present work, all the 12 branches ( ,
, 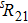 ,
,  ,
,  ,
,  ,
, 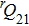 ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  ) of each band system were observed and analyzed to obtain the molecular constants for each vibration level. The
) of each band system were observed and analyzed to obtain the molecular constants for each vibration level. The  branch of the (8, 5) band has not be measured in this work. The assignment of the transitions follows the selection rules:
branch of the (8, 5) band has not be measured in this work. The assignment of the transitions follows the selection rules:  ; and
; and  ,
,  or
or  . The transitions are labelled as:
. The transitions are labelled as:  .
.
The Pgopher program[16] was used to fit the experimental data to get the molecular constants of the (8, 5), (3, 1), and (2, 0) bands of the  –
– system of
system of 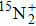 . In total, 677 rotational transition lines were assigned and fitted with the same weight, and shown in supplement part. The band labels, rotational J numbers of the observed lines, and the residual of the band origin are given in Table 1. The molecular constants of Av, Bv, Dv, pv, qv, ADv, and γv of the
. In total, 677 rotational transition lines were assigned and fitted with the same weight, and shown in supplement part. The band labels, rotational J numbers of the observed lines, and the residual of the band origin are given in Table 1. The molecular constants of Av, Bv, Dv, pv, qv, ADv, and γv of the  and
and  states of
states of  are listed in Table 2 and Table 3, respectively. Here, Av is the spin–orbit constant, Bv is the molecular rotational constant, Dv is the centrifugal distortion constant, ADv is the centrifugal distortion correction to Av, pv and qv are
are listed in Table 2 and Table 3, respectively. Here, Av is the spin–orbit constant, Bv is the molecular rotational constant, Dv is the centrifugal distortion constant, ADv is the centrifugal distortion correction to Av, pv and qv are  -doubling parameters, and γv is the spin-rotation parameter.
-doubling parameters, and γv is the spin-rotation parameter.
In Table 2, comparing our experimental results with other published ones, our molecular constants, Bv and Dv of the  state are in agreement with those of Reddy et al.[8] and Bernard et al.[12] except for γv values. For example, the experimental values of the γ parameter for the v = 0 of the
state are in agreement with those of Reddy et al.[8] and Bernard et al.[12] except for γv values. For example, the experimental values of the γ parameter for the v = 0 of the  state from Reddy et al.,[8] Bernard et al.[12] and our values are
state from Reddy et al.,[8] Bernard et al.[12] and our values are  ,
,  , and
, and  , respectively. We fitted the experimental data of Reddy et al. using Pgopher program, and gave a γ value of
, respectively. We fitted the experimental data of Reddy et al. using Pgopher program, and gave a γ value of  which is different with Reddy’s result. Bernard et al. pointed out that Reddy’s estimated value of
which is different with Reddy’s result. Bernard et al. pointed out that Reddy’s estimated value of  of the X state is from the analysis of the B–X system, the
of the X state is from the analysis of the B–X system, the  in the upper state,
in the upper state,  , is not statistically significant within 2σ limits. The
, is not statistically significant within 2σ limits. The  and
and  parameters are strongly correlated in the
parameters are strongly correlated in the  –
– transitions and only the
transitions and only the  –
– can be determined with confidence,[17] thus Reddy’s result of the γ in the
can be determined with confidence,[17] thus Reddy’s result of the γ in the  state is not realistic. However, in the
state is not realistic. However, in the 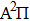 –
– transition, the γ in
transition, the γ in  state does not correlate significantly with any parameter in the upper
state does not correlate significantly with any parameter in the upper  state, so it can be properly determined in experiment. The values of the spin-rotation parameter, γ of Bernard’s and ours are in agreement with each other, Reddy’s and the “Fit” results are inconsistent with that of Bernard’s and ours.
state, so it can be properly determined in experiment. The values of the spin-rotation parameter, γ of Bernard’s and ours are in agreement with each other, Reddy’s and the “Fit” results are inconsistent with that of Bernard’s and ours.
Table 3 lists the molecular constants Av, Bv, Dv, pv, and qv of the  state. Our experimental ADv values of the v = 2 and 3 in the
state. Our experimental ADv values of the v = 2 and 3 in the  state are different with those of Bernard’s[12] both in magnitude and sign. The ADv value is determined by how the pv and qv values have been associated. In Bernard’s paper, they assumed that the
state are different with those of Bernard’s[12] both in magnitude and sign. The ADv value is determined by how the pv and qv values have been associated. In Bernard’s paper, they assumed that the  state interaction with the
state interaction with the  state,[12] and fixed the ADv values as 0.38 for both v = 2 and 3 of the
state,[12] and fixed the ADv values as 0.38 for both v = 2 and 3 of the  .
.
3.2. Isotope shiftsThe observed isotope shifts of the (2, 0), (3, 1), and (8, 5) bands of the A–X system of  were obtained directly from the differences between our observed lines of
were obtained directly from the differences between our observed lines of  and the reported experimental lines[18] of
and the reported experimental lines[18] of  of this Meniel system.
of this Meniel system.
The calculated isotope shifts were determined using the following expression:
where
ν is the transition frequency,
v is the vibrational quantum number, “

”and “

” refer to the upper and lower states,
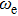
,
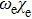
, and
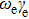
are the equilibrium molecular constants. The value of the isotope parameter,
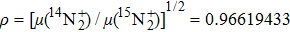
.
[19]The observed and calculated band origins and isotope shifts of the (2, 0), (3, 1), and (8, 5) bands of the A–X system of  and
and  are listed in Table 4. The band origins of
are listed in Table 4. The band origins of  and
and  are obtained from our previous[18] and the present experimental results, respectively. The measured isotope shifts (labbled with
are obtained from our previous[18] and the present experimental results, respectively. The measured isotope shifts (labbled with  ) are extracted from the experimental values of the band origins of
) are extracted from the experimental values of the band origins of  and
and  directly. The calculated isotope shifts are calculatedusing equation (1) with several experimental equilibrium molecular constants.[7,18,20] The observed values of the isotope shifts are in agreement with those of the calculated.
directly. The calculated isotope shifts are calculatedusing equation (1) with several experimental equilibrium molecular constants.[7,18,20] The observed values of the isotope shifts are in agreement with those of the calculated.